随着社会的发展和工业技术的进步,国际社会对民用航空业的环保要求越来越苛刻,如何进一步降低飞机的噪声是民用航空业目前面临的一个重要问题。飞机的噪声主要包括发动机噪声和机体噪声两大类,在航空业发展的初期发动机噪声强度远高于机体噪声,但经过几十年的发展,发动机的喷流等噪声已经得到了显著的降低,这使得飞机的机体噪声达到和发动机噪声同等的水平,航空界也越来越重视机体噪声的研究与降噪。其中,增升装置是飞机降落时主要的中低频率噪声源,研究增升装置的噪声机理、噪声影响因素以及降噪措施等对降低机体具有重要意义[1-3]。目前,国外一些学者已经通过风洞实验和数值计算等手段对增升装置噪声的机理、特性进行了研究,阶段性研究结果显示增升装置噪声与增升装置较复杂的几何结构、复杂湍流流动和声传播现象有关[4-7]。
关于增升装置等机体噪声数值模拟工作,吕宏强[8]在高阶间断有限元方面进行了研究,并用该方法进行了NACA0012、多段翼型和空腔流动气动噪声分析;郭跃平[9]建立了襟翼侧缘噪声计算模型,并对其进行了CAA计算分析;Rajani Satti等[10]采用基于格子-玻尔兹曼方程的非定常流场(LBM-VLES)计算方法,提取出了高升力装置的压力脉动信息,获得了近场声场结果;Rakhshanil B等[11]采用专用模型分析方法计算增升装置气动噪声;Ewert R等[12]提出源于RPM(Random Particle Mesh,RPM)的CAA方法可能是适合缝翼噪声传播计算的方法;Nicolas Molin等[13]采用RANS/LES结合FW-H方程来计算缝翼产生的气动噪声。
目前最为实用的气动噪声计算方法是“CFD+声类比”方法,该方法的基本思想是:首先,基于计算流体力学方法计算获得运动物面的非定常压力分布[14-16],甚至是湍流边界层内的非定常流场,然后基于求解FW-H方程获得远近声场分布[17]。该方法是目前以及未来一段时间内最实用和最理想的噪声预测方法。
由于声学计算结果的精度很大程度上取决于流场计算的精度,选择合适的流场计算方法十分重要。目前气动声学常用的流场计算方法有非定常雷诺平均模拟(URANS)、分离涡模拟(DES)、大涡模拟(LES)和直接数值模拟(DNS)。URANS方法提供的流动细节和计算精度的级别最低,虽可捕捉大尺度流体运动及其产生的噪声,但不能得到宽带声源信息。DES方法对离物体表面稍远的分离涡的模拟有着较高的精度,性价比较高,是目前声学数值计算最常用的方法,但对于离物面较近的影响声源产生的流动结构模拟有一定的局限性。DNS方法要求计算网格的尺度和最小旋涡的尺度相当,网格规模、消耗的计算资源巨大。LES通过显示表达大尺度的湍流脉动,而小尺度的湍流脉动则用模型化的方法来表达,较好解决了DNS网格量过于庞大的问题。
本文通过圆柱绕流算例,与文献中的试验结果进行了对比,验证了本文气动声学数值计算方法的可靠性与准确性。采用LES方法对增升装置的非定常流场进行数值模拟,采用可穿透积分面的Ffcows Wil1iams-Hawkings积分方法进行远场噪声计算,对增升装置噪声产生的流动特性、远场特性、风速影响等进行了数值模拟研究。
1 控制方程与数值方法 1.1 LES方法LES方法的中心思想是将比网格尺度大的湍流运动通过瞬时的NS方程直接计算出来,而小尺度涡对大尺度涡运动的影响则通过一定的模型在针对大尺度涡的瞬时NS方程中体现出来。
在LES方法中,每个变量被分为两部分,对瞬时变量φ,有
 (1)
(1) 式(1)中,φ为大尺度的平均分量,由直接计算得到,采用滤波函数对其进行处理,有φ=∫DφD(x, x′)dx′,其中D为流动区域,x是滤波后大尺度空间上的空间坐标,x′是实际流动区域中的空间坐标,D(x, x′)决定了所求解的涡的尺度,即将大涡与小涡分离开来。φ′表示小尺度分量,需要通过模型来表示。
用上面的滤波函数D(x, x′)处理瞬时状态的NS方程,可得到:
 (2)
(2)  (3)
(3) 式中带有上划线的量为滤波后的流场变量,其中,τij为亚格子尺度应力,简称SGS应力,它体现了小尺度涡运动对所求解NS方程的影响。
根据Smagorinsky的基本SGS模型[18],假定SGS应力具有下面的形式:
 (4)
(4) 式中,μt=(CsΔ)2|S|为亚格子尺度的湍动粘度。
 (5)
(5)  (6)
(6)  (7)
(7) 式中,Δx代表沿x轴方向的网格尺寸,CS是Smagorinsky常数。
1.2 基于FW-H方程的声类比方法声类比混合计算方法的特点在于流场和声场计算是分离的,其基本思想是基于流场到声场的单向耦合,即非定常流动产生声波并改变其传播,但声波对流场却没有显著的影响。预测气动噪声的FW-H声类比方法是指在获得近场流动解的基础上,将近场流动解作为声源信号,运用FW-H公式积分求得远场观测点处的气动噪声。
 (8)
(8) 其中, vn、un为控制面的法向运动速度和流体的法向运动速度,H(f)为Heaviside函数,δ(f)为狄拉克函数,定义为:
 (9)
(9) 令:
 (10)
(10) 便可以得到FW-H方程的解:
 (11)
(11) 其中,厚度噪声和载荷噪声的表达式如下:
 (12)
(12) 载荷噪声的表达式为:
 (13)
(13) 该积分公式所用的声学积分面可以是任意的包含固体的空间曲面,当声学积分面取固体表面时,公式中的各个积分项仍具有厚度噪声、载荷噪声的物理意义;若公式的声学积分面包含固体边界附近的非线性流动,则单极子、偶极子的积分项将失去其物理意义,而仅具有数学意义,但此时四极子声源对声的贡献将从面积分中得到体现,即通过面积分求得了总的气动噪声[21-22]。
2 计算方法验证由翼型的噪声机理可知,翼型噪声源主要是偶极子声源,与此类似的是,圆柱绕流噪声是由周期性的脱落涡造成的,也是一个典型的偶极子噪声,因此,采用LES+FW-H的方法计算圆柱绕流噪声,以此验证流场计算方法与声场计算方法的正确性。
参照Revell[23]试验中所用的模型,圆柱直径D=0.019m,圆柱展向长度L=0.5m,来流马赫数Ma=0.2,雷诺数Re=90000。圆柱网格如图 1所示。

|
| 图 1 圆柱网格示意图 Fig. 1 Grid of cylinder |
图 2为本文计算得到的升阻力系数随时间变化的历程,可以看出,阻力系数的波动周期约为升力系数的一半左右。由于CFD数值格式本身的耗散性较大,无法准确捕捉到远场的脉动量,但对壁面处的脉动量一般能够较准确地捕捉到。表 1为本文LES计算结果与试验结果及文献LES计算结果[24]的对比,主要对比了涡脱落频率、升力系数脉动量的均方根和时均阻力系数,可以看出本文和文献计算结果均与试验结果符合较好。本文升力系数脉动量的均方根与文献计算结果的误差约为4.12%左右,且在试验结果的范围之内,本文中的LES方法在时间、空间上均采用的是二阶计算格式,因此,说明了本文二阶精度的LES非定常流场计算已经能够准确地捕捉到壁面的脉动量信息。

|
| 图 2 圆柱的升阻力系数随时间变化的历程 Fig. 2 Time histories of lift and drag coefficients of cylinder |
根据Revell试验的设定,声的观测点选定在圆柱的中截面、垂直于来流方向、距离圆心128D的位置。图 3为观测点处,本文的频谱计算结果与试验结果及文献计算结果的对比,由图中可以看出,无论是声压级的峰值与频率还是声压级的走势,本文计算结果与文献计算结果[24]均与Revell的试验结果[23]吻合得很好,说明了本文所采用的LES+FW-H方法能够较准确地计算湍流脉动量及由此而产生的气动噪声,同时也再一次验证了本文所采用的LES二阶计算格式能够准确地捕捉到壁面的脉动量信息。

|
| 图 3 观测点处本文的频谱计算结果与Revell等试验结果及Kato等LES+FW-H计算结果的对比 Fig. 3 Comparison of sound pressure level spectrum at receiver point obtained from experimental results of Revell et al., LES+FW-H results of Kato et al.and LES+FW-H results of this paper |
3 增升装置模型与计算网格 3.1 增升装置模型
本文采用英国国家高升力项目二维L1T2模型,如图 4所示,缝翼偏角δslat为25°,襟翼偏角δflap为20°,参考弦长为缝翼和襟翼闭合时的翼型长度1m。

|
| 图 4 二维多段翼L1T2模型图 Fig. 4 Model of two dimensional multi-element high lift device L1T2 |
3.2 计算网格
全场网格及局部网格如图 5~图 7所示,为二维结构化网格,缝翼、主翼和襟翼分别分布214、680和181个网格点,网格总量约为110万,第一层网格高度为10-6m,在缝翼空腔以及后缘处的网格进行加密,保证多段翼表面各处y+ < 1。其中声源积分面的网格以网格交界面的形式生成出来,以便每一个时间步将声源积分面的流场信息单独输出,避免由于插值而带来的数值误差,声源积分面位置的设定如图 8所示。

|
| 图 5 L1T2多段翼网格 Fig. 5 Grid of L1T2 |

|
| 图 6 缝翼附近的网格 Fig. 6 Grid near slat |

|
| 图 7 襟翼附近的网格 Fig. 7 Grid near flap |

|
| 图 8 L1T2多段翼声源积分面位置 Fig. 8 Position of sound soure integral surface of L1T2 |
4 计算结果分析
本文将计算结果分为气动和流场特性、气动噪声特性两部分,与相应的试验气动特性进行对比,并通过流场特性分析噪声产生的主要原因。
计算条件为:模型迎角为20°,来流风速为60m/s 、70m/s、80m/s。在流场的数值计算中,采用基于SA湍流模型的RANS方法计算增升装置的稳态流场,为LES计算提供较为合理的初始值,接下来引入双时间迭代进行非定常计算,空间离散采用耦合TVD限制器的二阶迎风格式,时间离散采用二阶隐式格式。非定常计算的时间步长为Δt=2.5×10-5s,时间推进10000步到0.25s时,非定常流动呈现相对稳定的周期性特征,此时开始记录气动特性、流动参数和声源积分面数据,再推进8000步至0.45s,LES计算完成(时均结果都是在0.25s到0.45s内求时间平均得到的)。
记录声源数据时间步数n=8000步,声源积分面的流场数据的记录总时间为0.2s,即经过FFT变化的声压级频谱曲线频率的分辨率为5Hz。
4.1 气动及流场特性分析图 9为LES计算得到的风速70m/s,模型迎角20°下升力系数随时间的变化历程,升力系数时均结果为3.994(文献[27]风洞试验值为4.072);图 10为表面时均压力系数与文献[28]试验结果的对比。可看出本文流场数据计算结果与试验结果吻合较好。

|
| 图 9 多段翼L1T2的升力系数随时间变化的历程(来流风速70m/s,迎角20°) Fig. 9 Time historiy of lift coefficient of L1T2 (flow velocity is 70m/s, attack angle is 20°) |

|
| 图 10 增升装置表面时均压力系数分布(来流风速70m/s,迎角20°) Fig. 10 Distribution of surface time-averaged mean pressure coefficient of high lift device(flow velocity is 70m/s, attack angle is 20°) |
图 11为来流风速70m/s、迎角20°下,多段翼L1T2某时刻下的压力云图和涡量云图。可以看出:缝翼后缘脱落的涡以及流动在缝翼和主翼之间的凹槽形成的不稳定波是缝翼附近产生噪声的主要原因;而襟翼附近由于流动分离产生的高频的小尺度不稳定涡和低频的大尺度涡,则是襟翼附近产生噪声的主要原因。

|
| 图 11 多段翼L1T2的瞬时压力、涡量云图 Fig. 11 The instantaneous pressure and vorticity distribution nephogram of L1T2 |
当缝翼逐渐打开时,在缝翼和主翼之间会渐渐形成一个向下方逐渐扩大的空腔,流动在缝翼的下方尖端处形成一个不稳定的剪切层,在空腔处会形成明显的涡。为研究空腔处产生的涡的特性,在空腔处设置了一个监测点,如图 12所示。监测点处的静压随时间变化历程如图 13所示。可以看出,空腔中形成的涡具有明显的周期性,并且周期约为0.005s,即频率约为200Hz。

|
| 图 12 监测点位置示意图 Fig. 12 Schematic diagram of monitoring point |

|
| 图 13 监测点处静压随时间的变化历程 Fig. 13 Change history of static pressure at monitoring point with time |
由于缝翼空腔处涡运动的周期约为0.005s,因此,取t=0.335s、0.336s、0.337s、0.338s时刻的数值解来分析缝翼空腔处的流场。图 14为缝翼空腔处在这四个不同时刻下的涡量云图。可以看出,缝翼附近的流场特性很复杂。缝翼尖端或在缝翼凹面区域的流动分离形成了极不稳定的剪切层,剪切层的不稳定性首先导致线性幅度增大,最终导致湍流的非线性饱和。这种饱和在剪切层中形成了卷起涡和离散涡,这些涡通过缝翼空腔向上方移动。空腔处涡的流动经过了强烈的波动后成为中低频噪声源。除此之外,由于缝翼后缘的厚度是有限的,因此会导致在缝翼后缘会产生一系列小涡的交替脱落,这些小涡脱落将是高频纯音中的一个重要组成部分。

|
| 图 14 缝翼空腔处的瞬时涡量云图(来流风速70m/s,迎角20°) Fig. 14 Instantaneous vorticity distribution nephogram of the cavity near slat(flow velocity is 70m/s, attack angle is 20°) |
4.2 远场气动噪声特性分析
在距离模型10m处,每隔10°取一个观测点,计算得到的多段翼L1T2总的噪声、缝翼噪声以及襟翼噪声的指向性如图 15所示。可以看出,缝翼的噪声辐射强度大于襟翼,并且缝翼和襟翼的声指向性图呈现出明显的偶极子样式,说明偶极子噪声为其主要的噪声源。除此之外,二者的指向性虽然有所不同,但有一个共同点,即均在垂直于各自轴线的方向处达到最大值。
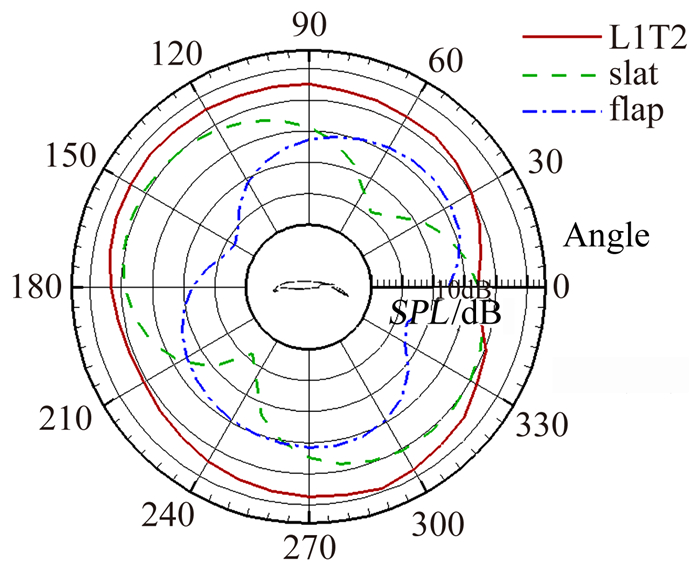
|
| 图 15 多段翼L1T2不同部件的声指向性图对比(来流风速70m/s,迎角20°) Fig. 15 Sound directivity diagrams of different elements(flow velocity is 70m/s, attack angle is 20°) |
在垂直于多段翼轴线方向,取多段翼正下方10m处的点为监测点,图 16为不同风速下监测点处增升装置噪声的三分之一倍频程频谱,由于本次数值模拟是二维的,所以不包含襟翼侧缘产生的噪声。可以发现在200Hz左右的低频段,均有一个较明显的尖峰,该频率与缝翼空腔中的涡运动频率一致,证明该纯音产生与缝翼空腔非定常的涡结构和高升力构型之间的交互作用有关;而中高频段部分,主要来源于襟翼后缘的涡脱落以及缝翼有限厚度钝尾缘的小涡脱落。

|
| 图 16 不同风速下的多段翼L1T2噪声的三分之一倍频程频谱(迎角20°) Fig. 16 Sound pressure level spectrums in 1/3-octave band of L1T2 at different flow velocities (attack angle is 20°) |
图 17为不同风速下多段翼L1T2的总噪声指向性对比。可以看出声指向性具有偶极子特性,在300°左右即缝翼下表面噪声辐射方向声压级达到最大,该方向也是缝翼噪声辐射最大值的方向,说明缝翼噪声是增升装置噪声的重要组成部分。按偶极子强度与马赫数的六次方成正比的规律来推算,风速60m/s和70m/s、70m/s和80m/s的总声压级之差分别为4dB、3.5dB,本文数值计算结果分别为4.2dB、3.9dB,两者比较吻合,表明数值计算结果满足偶极子的六次方定律。

|
| 图 17 多段翼L1T2不同风速下的声指向性图对比(迎角20°) Fig. 17 Sound directivity diagrams of L1T2 at different flow velocities (attack angle is 20°) |
5 结论
本文采用LES方法对增升装置流场进行数值模拟,并利用可穿透积分面的Ffcows Wil1iams-Hawkings积分方法进行远场噪声计算。采用圆柱绕流算例对本文的数值计算方法进行了验证,并分析了增升装置产生噪声的机理,得到了以下几点结论:
1) LES方法能够准确捕捉到涡脱落、流动分离等非定常流动现象,并且可以准确模拟特征尺度较小的湍流涡,能够为远场气动噪声计算提供精确的声源及近场流动信息;
2)在近场声源积分面的流动数据准确的前提下,基于FW-H的声类比方法能够精确高效求解远场气动噪声;
3)缝翼产生气动噪声的主要原因是缝翼后缘脱落的涡以及流动在缝翼和主翼之间的凹槽形成的不稳定波;在声压级频谱中,200Hz左右出现明显的纯音,频率与缝翼空腔处涡运动的频率相一致;
4)襟翼产生气动噪声的主要原因襟翼附近由于流动分离产生的高频的小尺度不稳定涡和低频的大尺度涡;
5)声学计算得到的迎角20°时缝翼和襟翼噪声均在垂直于各自轴线的方向处达到最大值,多段翼L1T2及其部件声指向性图与偶极子的相关特性吻合,多段翼L1T2的指向性最大值方向与缝翼一致,并且满足偶极子的六次方定律。
| [1] | Philip J M, Lyle N L, Ashok B, et al. A parallel three-dimensional computational aeroacoustics[J].Journal of Computational Physics, 1997, 133:56–74.DOI:10.1006/jcph.1997.5646 |
| [2] | Inoue O, Hatakeyama N. Sound generation by at two-dimensional circular cylinder in an uniform flow[J].Journal of Fluid Mechanics, 2002, 471(1):285–314. |
| [3] |
Hu G Q, Fu D D, Ma Y W. Numerical simulation of noise generated by flow past an airfoil using acoustic analogy[J].Acta Mechanica Sinica, 2000, 32(4):393–410. (in Chinese) 胡国庆, 傅德黛, 马延文. 基于比拟理论的翼型扰流声场数值模拟[J]. 力学学报, 2000, 32(4) : 393–410. |
| [4] | Lighthill M J. On sound generated aerodynamically I. General Theory[C]//Proceedings of the Royal Society of London, 1952, A211: 564-587. |
| [5] |
Yu P X, Bai J Q, Huang J T, et al. Aerodynamic noise of the rod-airfoil computed by using acoustic analogy[J].Acta Aerodynamica Sinica, 2013, 31(2):204–208. (in Chinese) 余培汛, 白俊强, 黄姜涛, 等. 基于比拟理论计算圆柱/翼型的气动噪声[J]. 空气动力学学报, 2013, 31(2) : 204–208. |
| [6] |
Yu L, Song W P, Yan L. An effective method for predicting aerodynamic noise for wind turbine flat back airfoils[J].Journal of Northwestern Polytechnical University, 2012, 30(4):513–517. (in Chinese) 余雷, 宋文萍, 闫利. 平底后缘风力机翼型气动噪声计算研究[J]. 西北工业大学学报, 2012, 30(4) : 513–517. |
| [7] |
Han Z H, Song W P, Qiao Z D. Aeroacoustic calculation for helicopter rotor in hover and in forward flight based on FW-H equation[J].Acta Aeronautica et Astronautica Sinica, 2003, 24(5):400–404. (in Chinese) 韩忠华, 宋文萍, 乔志德. 基于FW-H方程的旋翼气动声学计算研究[J]. 航空学报, 2003, 24(5) : 400–404. |
| [8] |
Lyu H Q, Zhu G X, Song J Y, et al. High-order discontinuous galerkin solution of linearized Euler equations[J].Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3):621–624. (in Chinese) 吕宏强, 朱国祥, 宋江勇. 线化欧拉方程的高阶间断有限元数值解法研究[J]. 力学学报, 2011, 43(3) : 621–624. |
| [9] | Guo Y P. Aircraft flap side edge noise modeling and prediction[C]//17th AIAA/Ceas Aeroacoustics Conference, Portland Oregon: American Institute of Aeronautics and Astronautics, 2011: 2011-2731. http://cn.bing.com/academic/profile?id=2314075046&encoded=0&v=paper_preview&mkt=zh-cn |
| [10] | Satti R, Li Y B, Shock R. Aeroacoustics analysis of a high-lift trapezoidal wing using a lattice boltzmann method[C]//14th AIAA/CEAS Aeroacoustics Conference, British Colmbia Canada: American Institute of Aeronautics and Astronautics, 2008: 2008-3048. |
| [11] | Rakhshanil B, Filippone A. Noise from high-lift leading-edge device[C]//24th AIAA Applied Aerodynamics Conference, San Francisco, California: American Institute of Aeronautics and Astronautics, 2006: 2006-3844. |
| [12] | Ewert R. Slat noise trend predictions using CAA with stochastic sound sources from a random particle mesh method (RPM)[C]//12th AIAA/CEAS Aeroacoustics Conference, Cambridge Massachusetts: American Institute of Aeronautics and Astronautics, 2006: 2006-2667. |
| [13] | Nicolas Molin. Prediction of aircraft high-lift device noise using dedicated analytical models[C]//9th AIAA/CEAS Aeroacoustics Conference and Exhibit, Hilton Head South Carolina: American Institute of Aeronautics and Astronautics, 2003: 2003-3225. |
| [14] | Rodi W. Comparison of LES and RANS calculations of the flow around bluff bodies[J].Journal of Wind Engineering and Industrial Aerodynamicist, 1997(69-71):55–75. |
| [15] | Kang H S, Chester S, Meneveau C. Decaying turbulenee in an active-grid-generated flow and comparisons with large-eddy simulation[J].Journal of Fluid Mechanics, 2003, 480:129–160.DOI:10.1017/S0022112002003579 |
| [16] | Khalighi Y. Prediction of sound generated by complex flows at low mach numbers[J].AIAA Journal, 2010, 48(2):306–316.DOI:10.2514/1.42583 |
| [17] | Lighthill M J. On sound generated aerodynamically. II. Turbulence as a source of sound[C]//Proceedings of the Royal Society of London, 1954, 222: 1-32. http://cn.bing.com/academic/profile?id=2111597484&encoded=0&v=paper_preview&mkt=zh-cn |
| [18] | Ewert R, Schroder W. On the simulation of trailing edge noise with hybrid LES/APE method[J].Sound Vibration, 2004, 270:509–524.DOI:10.1016/j.jsv.2003.09.047 |
| [19] | Inoue O, Hatakeyama N. Sound generation by a two-dimensional circular cylinder in an uniform flow[J].Journal of Fluid Mechanics, 2002, 471(1):285–314. |
| [20] | Ffowcs Williams, Hawkings J E. Sound generated by turbulence and surfaces in arbitrary motion[J].Philosophical Transactios of the Royal Society, 1969, 264(1151):321–342.DOI:10.1098/rsta.1969.0031 |
| [21] | Brooks T F, Hodgson T H. Trailing edge noise Prediction using measured surface pressure[J].Joumal of Sound and Vibration, 1981, 78(1):69–117.DOI:10.1016/S0022-460X(81)80158-7 |
| [22] | Günther B, Becker R, Carnarius A, et al. Simulation study of the robust closed-loop control of a 2D high-lift configuration[J].IUTAM Symposium on Unsteady Separated Flows and their control, 2009, 14:505–516.DOI:10.1007/978-1-4020-9898-7 |
| [23] | Revell J D, Prydz R A, Hays P. Experimental study of airframe noise vs. drag relationship for circular cylinders[R]. Lockheed Report 28074, 1997. |
| [24] | Kato C, Yamade Y, Wang H, et al. Numerical prediction of sound generated from flows with a low mach numer[J].Computer & Fluids, 2007, 36(1):37–68. |
| [25] | Norberg C. Fluctuating lift on a circular cylinder: review and new neasurements[J].Fluids and Structures, 2002, 17(1):57–96. |
| [26] | Cantwell B, Coles D. An experimental study of entrainment and transport in the turbulent near wake of circular cylinder[J].Journal of Fluid Mechanics, 1983, 136(4):321–374. |
| [27] | Moir I. Measurements on a two-dimensional aerofoil with high-lift devices[R]. AGARD AR-303, 1994(2): 58-59.. |
| [28] | Balaji R, Bramkamp F, Hesse M, et al. Effect of flap and slat riggings on 2-D high-lift aerodynamics[J].Journal of Aircraft, 2006, 43(5):1259–1271.DOI:10.2514/1.19391 |


