0 引 言
栅格翼[1]是一种特殊的气动构件,由小弦长的框架及在其内部交叉放置的细薄翼面构成。与传统平板翼面相比,栅格翼将升力面由平面分布发展为空间分布,布局更为紧凑,因此具有铰链力矩小、升力特性优良、结构承力合理等特性。栅格翼研究在航空航天 领域日益得到重视[2]。前苏联在20世纪50年代开 始研究栅格翼,栅格翼的应用最为广泛,除了“联盟号”飞船以外,在空空导弹、洲际弹道导弹等广泛的领域都得到了应用。西方国家关于栅格翼的研究工作是从20世纪80年代中后期开始的。美国陆军航空兵与导弹司令部研究发展与工程中心从1985年到1997年通过9项风洞试验对栅格翼布局导弹的气动特性进行了广泛研究,内容包括基本性能研究、作为控制舵面气动特性、减阻技术、参数影响分析、飞行器应用、滚转阻尼研究、隔板和弹体的影响等。试验马赫数0.3~3.5,共涉及外形26种,其研究外形BOAR(火箭发射BAT反坦克弹)弹头已进行了两次飞行试验和一次挂机投放飞行试验。国内在神舟号飞船逃逸舱上也进行了应用,并参加了神舟1号到神舟7号飞船任务[3]。
早期栅格翼空气动力特性的研究以风洞试验和工程估算为主。近十几年来,随着计算机和计算技术的飞速 发展,计算流体力学(CFD)已成为工程设计的有力手段。CFD技术在栅格翼气动特性研究上的主要难点是:对于栅格翼的蜂窝式结构,多组翼片交错排列,传统的分区结构网格技术建模十分困难、生成的网格规模庞大。重叠网格[3]、混合网格[4]的技术发展,为栅格翼气动特性数值模拟提供了较好的解决方案。
本文采用结构/非结构混合网格方法,研究了某栅格翼气动布局,对典型状态流场和气动性能进行了分析,并且对跨声速状态下的栅格壅塞现象进行了解释,数值计算情况与风洞试验研究结果一致。 1 栅格翼气动特性
栅格翼的空气动力学特性依赖于来流条件和栅格几何参数(如图 1所示)。一般认为,当来流从亚声速到超声速变化时,存在三个特征马赫数,当气流在栅格某截面达到声速进而出现正激波时,伴随阻力增大,称第一临界马赫数(图 1a)。随马赫数增大至超过声速的某值时,通道内正激波前移并脱体,使升力减小、阻力增大。马赫数继续增大,激波逐渐向栅格前缘靠近,至附体时称第二临界马赫数(图 1b)。此后栅格内出现多次反射的斜激波系,当马赫数增至第三临界马赫数(图 1d),无反射激波,此后栅格舵的流动特性不再出现实质性的变化[6]。
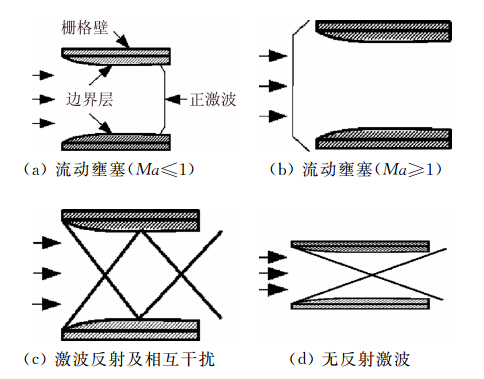 |
| 图 1 栅格流动状态Fig. 1 Grid fin flow regimes |
亚声速栅格(来流小于第一临界马赫数)和超声速栅格(来流大于第二临界马赫数)具有良好的空气动力线性特征,也是人们研究较多的情况。文献[7]将亚声速栅格看做一个空间分布的离散附着涡系和自由涡系的升力面系统,采用涡格法作工程估计。文献[8]采用超声速薄翼理论计算来流大于第三临界马赫数的情况,并对第二临界马赫数到第三临界马赫数 时栅格间存在波系干扰的情况进行修正,获得较好结果。
跨声速栅格(来流介于第一、二临界马赫数之间)流动状态远较其它两种情况复杂,由于通过栅格的气流受壁面约束明显,存在跨声速壅塞问题。由壅塞的定义,在通道流动中任一截面单位时间内流过的质量流量守恒。由于表征热力学参量的密度和表征运动学参量的流速总成反变关系,流体在亚声速和超声速时压缩性强弱不同,使质量流量密度随流速增加呈先增后减趋势,在声速时存在拐点,有最大值。对于收缩-扩张通道,在最小截面即喉道处达到声速,能获得喉道处允许通过的最大质量流量,若进口处流量大于这个值,多余的流体无法通过喉道,即发生了壅塞。文献[9]指出,在跨声速临界马赫数附近,栅格翼上出现网状激波和流动壅塞现象,使俯仰力矩和法向力发生剧烈变化,从而导致动态特性变差。
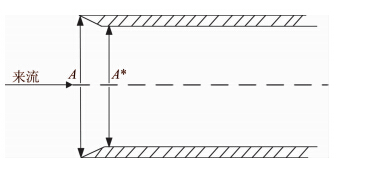 |
| 图 2 栅格中面积比Fig. 2 Area ratio of grid fin |
如果流动通道收缩主要由栅格格片厚度引起,可以采用一维等熵流关系式估计栅格进入壅塞状态的临界马赫数,参见式(1)。等熵流关系式在数学上有大于1和小于1的两个解,对应的物理现象为超声速气流和亚声速气流分别可以通过收缩通道达到声速。因此壅塞问题应存在两个临界马赫数,亚声速解表示 栅格进入壅塞的下临界状态,超声速解表示栅格退出 壅塞状态的上临界状态[10, 11]。
2 计算方法 2.1 混合网格高质量的网格生成是CFD研究的关键因素。对栅格翼外形,由于多组翼片交错排列,采用分区结构网格技术拓扑划分极为困难,即使勉强生成也会出现网格量大、网格质量差等问题。文献[12]采用非结构网格研究栅格翼,非结构网格由于摒弃了网格节点的结构性限制,具有很强的几何灵活性,易于生成复杂外形网格,但缺点是存储和计算效率低,粘性模拟能力差。
为扬长避短,结合结构网格和非结构网格各自的优缺点,人们提出了混合网格的思想。混合网格方法包括:三棱柱/四面体混合网格[13]、四面体/三棱柱/金字塔/六面体混合网格[14]、笛卡尔/四面体混合网格[15]和笛卡尔/四面体/三棱柱混合网格[16]等。
本文采用的混合方法是先对弹体和栅格翼分别独立生成互不相交的结构网格子块,各子块网格采用非结构 网格进行填充,满足非结构网格和结构网格交接面的完全对接。当改变栅格翼的舵偏角时候,弹身和栅格翼上的结构网格保持不变,只需要重新自动生成填充部分的非结构网格。这种混合网格结构能较好处理栅格翼偏转、任意栅格翼组合等复杂工况,简化了网格生成难度、有效减少了网格生成人工工作量。 2.2 求解器
本文算例均求解雷诺平均NS方程,空间离散采用 Roe的FDS格式,MUSCL插值方法和Van Albada限制器用 于获得二阶空间离散精度;湍流模型采用SST模型;时间离散采用稳定性高的LU-SGS隐式计算方法。关于数值方法的详细介绍参见文献[17]。 3 计算模型
研究的某栅格翼气动布局外形弹体由幂次曲线形头部和圆柱后体组成,4片栅格尾翼呈十字布置。图 3、图 4是网格示意图,弹体和栅格翼分别生成贴体结构网格,弹体网格数目为176.65万,单个栅格翼为142.16万。填充的非结构网格数目约237万。
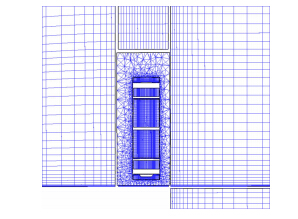 |
| 图 3 栅格翼纵截面混合网格Fig. 3 Longitudinal section hybrid grid |
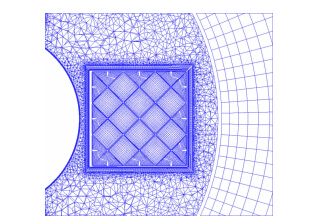 |
| 图 4 栅格翼横截面混合网格Fig. 4 Cross section hybrid grid |
图 5是单独一组栅格在亚声速条件下流场等马赫数云图和压力云图。在亚声速来流下,气流能从栅格顺畅通过,栅格对来流作用相当于薄物体扰动,格片前缘肩部处气流加速作用明显。在栅格通道内部,由于亚声速气流压缩后热力学参数减小、动力学参数增大,故通道内气流相对未扰动气流,压力稍低而马赫数略高。
 |
| 图 5 Ma=0.85栅格流场图Fig. 5 Ma=0.85 grid fin flow field |
图 6是单独一组栅格在超声速条件下流场等马赫数云图和压力云图,可以看到当来流马赫数介于第二临界马赫数和第三临界马赫数之间时,栅格前缘斜激波系角度较大,激波在相邻栅格间发生相交、反射,并在通道内产生弱的压缩波系和膨胀波系,以及结尾激波。
 |
| 图 6 Ma=1.5栅格流场图Fig. 6 Ma=1.5 grid fin flow field |
对第3节所述栅格翼气动布局导弹在超声速流动下,开展了不同控制舵偏条件的常规风洞测力试验。图 7给出了部分工况下风洞试验数据和混合网格计算结果的比较情况。由图 7可以看出,计算结果与试验符合较好,数据曲线能正确反映气动性能规律,其中轴向力系数误差小于 15%,法向力系数和俯仰力矩系数符合较好,证明对栅格翼一类复杂气动构型,本文采用的混合网格方法达到了工程精度。
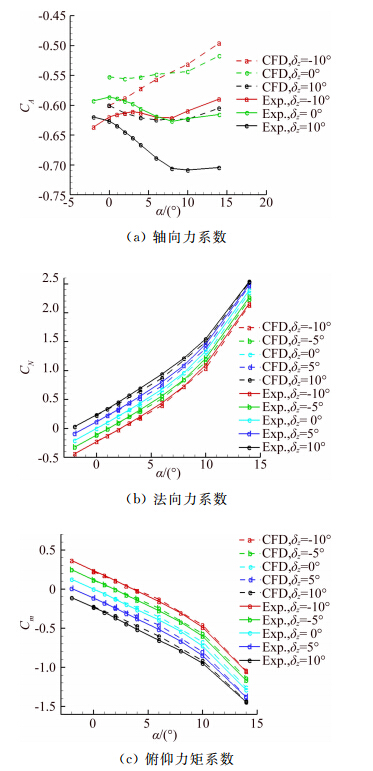 |
| 图 7 CFD和风洞试验数据比较(Ma=2.5,φ=0°)Fig. 7 Comparison of CFD and wind tunnel(Ma=2.5,φ=0°) |
图 8~图 10是单独一组栅格在跨声速条件下流场等马赫数云图和压力云图。当来流马赫数接近1时,通道内气流出现壅塞,多余流量对入口前流动产生反馈,入口处马赫数等值线逐渐密集,亚声速来流减速,流管扩张,部分流量从栅格外侧溢流。图 8中马赫数0.95时,在格片楔面与腹板转折处边缘气流发生扩张先达到超声速,并引射出膨胀波系,使中心区域气流加速至超声速流动,同时在通道末端出现结尾激波。当马赫数继续提高时,结尾激波将经后楔面膨胀与尾迹区压缩后,形成尾迹激波。
 |
| 图 8 Ma=0.95栅格流场图Fig. 8 Ma=0.95 grid fin flow field |
 |
| 图 9 Ma=1.13栅格流场图Fig. 9 Ma=1.13 grid fin flow field |
按一维理论,来流马赫数小于1时,栅格通道经前部楔面压缩不应出现超声速流动,三维情况是边缘气流先达到超声速,并使中心区域加速至超声速,反映了三维与一维问题的不同。壅塞导致的流量过剩,通过栅格前方亚声速气流减速扩张,部分流量从栅格外侧溢流而实现调节。
当来流大于1时,由于超声速气流“禁讯原理”,无法以扰动形式平缓地调整流量,而是通过激波改变入口流速和压力。此时栅格翼前方出现弱的网状脱体激波(如图 9所示),同时由于外部流场条件达到超声速,栅格翼后部的结尾激波消失。随马赫数提高,网状脱体激波逐渐向栅格翼靠近,当大于壅塞的上临界马赫数时,超声速气流能通过收缩通道,此时激波被吸附在栅格前缘上,如图 10所示。
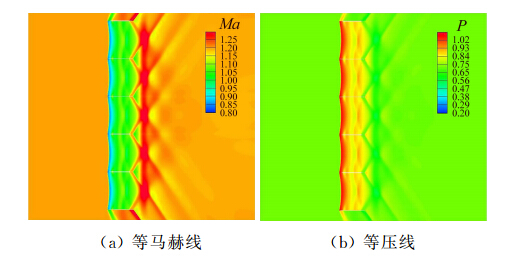 |
| 图 10 Ma=1.2栅格流场图Fig. 10 Ma=1.2 grid fin flow field |
栅格由下临界马赫数进入壅塞后,在来流马赫数 达到上临界前,将一直维持壅塞状态。由于上、下临界马赫数区间很窄,同时风洞试验存在雷诺数模拟不准的问题,因此只能通过数值计算在该区间加密来研究栅格翼的跨声速特性。事实上,文献[9]也指出,栅格翼跨声速壅塞只在数值模拟中出现,而风洞试验中无法复现。因此通过CFD开展了栅格翼在跨声速附件流动特性的研究。
为便于分析和比较,首先选取了一组栅格格片和单独一个格片(如图 11所示)进行对比研究。图 12是栅格格片和单格片在不同马赫数下气动性能比较,两者轴向力系数随马赫数均呈单峰变化趋势,但法向力系数有较大差异。低马赫速时栅格格片法向力系 数小于单格片,栅格通道对格片的壁面约束类似于两个“气垫”,使法向力变化更加平缓,这也是栅格翼在 大攻角时不易失速的原因。栅格进入壅塞状态后,法向力系数急剧下降,直至退出壅塞时法向力系数回 升,其间呈现一个变化平缓的凹坑形状,即壅塞区间栅格气动性能出现大幅度下降。
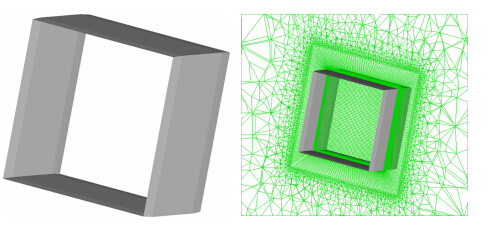 |
| 图 11 单栅格及其混合网格Fig. 11 Single fin and hybrid grid |
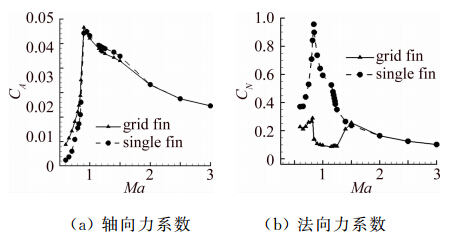 |
| 图 12 单独栅格和单格片气动性能比较Fig. 12 Aerodynamic characteristics comparison of grid fin and single fin |
图 13给出了混合网格计算的栅格翼布局导弹的翼面气动性能,参数变化趋势与图 12中一组栅格格片的规律一致。CN在马赫数0.9~1.2之间出现一个凹坑。结合前述流场分析可知,壅塞起一种自我调节的作用,通过溢流使通道内维持相似流动,使气动性能相对单格片的剧烈变化能保持平稳。但同时也是因为溢流使流量下降,栅格翼升力效率有较大减少,使全弹气动布局稳定性下降。
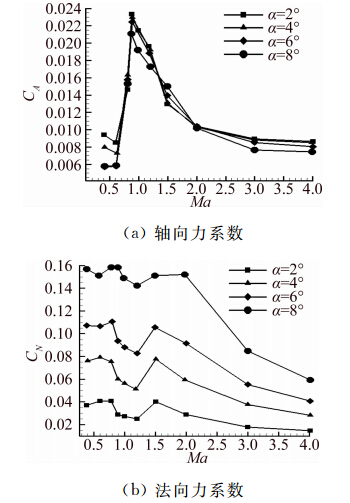 |
| 图 13 栅格翼布局导弹翼面气动性能Fig. 13 Grid fin aerodynamic characteristics of one missile |
针对所研究的栅格翼,下临界马赫数为0.8869,上临界马赫数为1.1206。图 14给出了下临界马赫数以下、上临界马赫数以上及其间三个典型马赫数的 单个栅格内的流动图画。图 15为质量流密度随马赫数的变化。由流动图画、质量流密度变化曲线可见,CFD计算结果与理论分析一致。
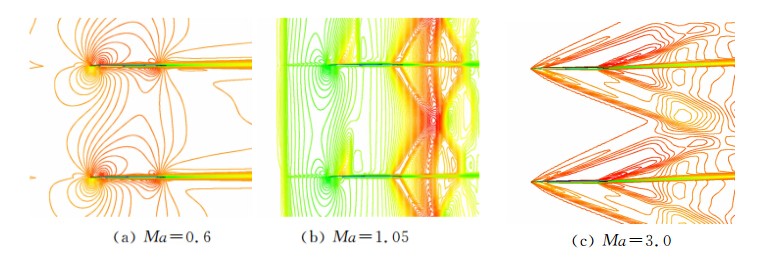 |
| 图 14 单个栅格内的等马赫线Fig. 14 Mach contours of single fin |
 |
| 图 15 质量流密度随马赫数的变化Fig. 15 Mass flow rate changing with Ma |
本文采用结构/非结构混合网格方法对栅格翼外形进行了研究,与风洞试验数据进行对比,验证了计算方法的正确性。主要结论有:
(1) 通过对栅格翼在亚跨超声速范围内典型流动状态进行的分析,重点解释了跨声速区栅格壅塞特性,指出壅塞导致的流量过剩,通过栅格前方亚声速气流减速扩张,部分流量从栅格外侧溢流而实现调节,超声速壅塞时,栅格翼上将产生网状脱体激波使来流减速再进行调节;
(2) 由一维理论计算的上、下临界马赫数,分别对应栅格翼进入、退出壅塞的临界点,估算值与数值模拟结果符合较好;
(3) 栅格翼进入壅塞区间后,由于流量下降,升力效率有较大减少,使气动布局稳定性下降。但由于壅塞的自调节作用,流动形态较为稳定,在壅塞区间内能保持气动特性的平缓变化。
| [1] | 贝洛齐尔科夫斯基. 栅格翼[M]. 中国运载火箭技术研究院, 译. 1994. |
| [2] | Li H H, Shi Y H. Current status and development trend of grid fin[J]. Missile and Space Vehicle, 2008, (6): 27-30. (in Chinese) 黎汉华, 石玉红. 栅格翼国内外研究现状及发展趋势[J]. 导弹与航天运载技术, 2008, (6): 27-30. |
| [3] | Cai Q Y, Ni J M. The aerodynamic simulation of max dynamic head test for the lattice wing of escape rocket[C]//Proceedings of the 1st National Conference on Mechanical Problems in the Field of Aerospace, 2004: 7-10. (in Chinese) 蔡巧言, 倪嘉敏. 逃逸飞行器栅格翼最大速度头试验的气动模拟[C]. 首届全国航空航天领域中的力学问题学术研讨会, 2004: 7-10. |
| [4] | Fan J J. Complex overlapping grid method and multi-body movement of the unsteady flow dynamic simulation[D]. Beijing: Beihang University, 2010. (in Chinese) 范晶晶. 复杂重叠网格方法研究及多体运动的非定常流动模拟[D]. 北京: 北京航空航天大学, 2010. |
| [5] | Liu G, Xiao Z Y, Jiang X, et al. Flow simulation of missile with grid fins using structured-unstructured hybrid grids[J]. Acta Aerodynamica Sinica, 2007, 25(2): 277-280. (in Chinese) 刘刚, 肖中云, 江雄, 等. 混合网格方法在栅格翼数值模拟中的应用研究[J]. 空气动力学学报, 2007, 25(2): 277-280. |
| [6] | Przemieniecki J S. Tactical missile design[M]. AIAA 2001. |
| [7] | Zhu Z X, Xu M. The aerodynamic calculation and analysis of subsonic grid fins[J]. Tactical Missile Technology, 1998, (1): 10-16. (in Chinese) 朱战霞, 徐敏. 亚声速栅格翼气动计算与分析[J]. 战术导弹技术, 1998, (1): 10-16. |
| [8] | Xu M, Zhu Z X. Analysis of supersonic aerodynamic characteristics on grid fins[J]. Tactical missile technology, 1999, (1): 1-6. (in Chinese) 徐敏, 朱战霞. 超声速栅格翼空气动力特性计算与分析[J]. 战术导弹技术, 1999, (1): 1-6. |
| [9] | Montgomery C H, Eric L B. Transonic aerodynamic analysis of lattice grid tail fin missiles[R]. AIAA 2006-3651, 2006. |
| [10] | Karl O. Aerodynamic analysis of lattice grid fins in transonic flow[D]. Ohio: Department of the Air Force Air University, 2004. |
| [11] | Anderson J D. Modern compressible flow: with historical perspective[M]. New York: McGraw-Hill Companies Inc. 2003. |
| [12] | James D, Harris L E. CFD analysis of grid fins for maneuvering missiles[R]. AIAA2000-0391, 2000. |
| [13] | Kallinderis Y, Khawaja A, Mcmorris H. Hybrid pris-matic/tetraheral grid generation for complex geometries[J]. AIAA J., 1996, 34: 291-298. |
| [14] | Coirier WJ, Jorgenson PCE. A mixed volume grid approach for the Euler and Navier-Stokes equations[R]. AIAA Paper 96-0762, 1996. |
| [15] | Zhang L P, Zhang H X, Gao S C. A cartesian/unstrutured hybrid grid solver and its application to 2D/3D complex inviscid flow fields[C]//ZHUANG F G, edited. Proceedings of the 7th International Symposium on CFD. Beijing, China: International Academic Publish-ers, 1997: 68-83. |
| [16] | Zhang L P, Yang Y J, Zhang H X. Numerical simulations of 3D inviscid/viscous flow fields on cartesian/unstructured/prismatic hybrid grids[C]//ZHANG H X, edited. Proceedings of the 4th Asian CFD Conference. Mianyang, China: University of Electronic Science and Technology of China Press, 2000: 93-103. |
| [17] | Yan C. Methods and application of computational fluid dynamics[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2006: 245-248. (in Chinese) 阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 245-248. |



