2. 中国科学院大学, 北京 100049;
3. 吉林大学地球探测科学与技术学院, 吉林 长春 130026
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. College of Geoexploration Science and Technology, Jilin University, Changchun 130026, China
月球天平动是月球自转、公转轨道以及周围天体对月球力的作用的综合表现。基于激光测月数据制作的月球历表是进行月球物理天平动研究的数据基础[1]。
根据卡西尼定则,月球的公转周期与自转周期一致,但由于月球质量的非球面分布,月球的自转并不是均匀的。这种与均匀旋转的偏离称为物理天平动。物理天平动有两种类型,受迫天平动和自由天平动。受迫天平动是由于地球、太阳和行星的引力引起的月球形状上的时变力矩;自由天平动主要是地质活动引起的,如冲击,核-幔相互作用,或是与受迫天平动的共振[2]。理论上,受迫天平动的振幅、相位和周期可以根据月球形状特征、弹性形变和旋转耗散计算。对于自由天平动,只能计算周期,振幅和相位必须通过测量获得[3]。
自由天平动有3种模式,一种在经度,两种在极位。经度模式是围绕月球极轴的周期为2.9年的摆状振荡[3]。极位模式描述了月球极位与周期为18.6年的受迫进动以及受迫天平动所决定的极位置之间的变化。第一个极位模式称为摆动模式,类似于地球的钱德勒摆动;另一个极位模式是自由进动模式,对应于空间中极轴周期为81年的运动。随着时间的推移,物理天平动由于能量耗散而逐渐减弱[4]。
月球物理天平动可以通过解析法和数值法两种方式计算。早期因为观测数据缺乏以及数值算法的计算量大,数值法相对于解析法并没有太大的优势,在工程上解析法的摄动理论完全可以达到精度要求[5]。但是随着深空探测的不断发展,对精度的要求逐渐提高,由于计算公式复杂,解析法开始显出劣势[6]。与此同时,在更多观测数据和计算机技术的支持下,数值法能达到更高的精度。随着地月数值历表的建立,数值法逐渐成为月球天平动研究的主要方法。月球历表包含月球在国际天球坐标系中位置和速度状态的信息[7-8],本文对月球轨道及物理天平动的研究所使用的数据均来自地月历表。
目前,我国月球探测已经进入月面着陆的快速发展期,特别是云南天文台和中山大学相继成功开展了月球激光测距试验,为我们加入国际月球激光测距分析社区提供了技术基础[8-9]。随着地面测月站数量的不断增加,国内激光测月向更高精度发展,未来会积累大量的高精度数据,这些数据为历表的研制和物理天平动的研究提供支撑。进入新世纪后,我国提出了月球和深空探测计划,并成功实施了月球探测项目。文[4]基于快速傅里叶变换,提出了一种频率提取和拟合的数值方法,从DE430历表提取月球自由天平动周期频率,与国际同行结果一致。在动力学模型方面,文[5-6]建立了基于国际上最新动力学模型的月球自转双层/单层模型及数值算法,结果精度与主流历表相当。本文使用最新的INPOP19a历表实现对月球物理天平动数据的提取。月球物理天平动数值模型精度的提高,为进一步高精度月球激光测距的研究打下基础。
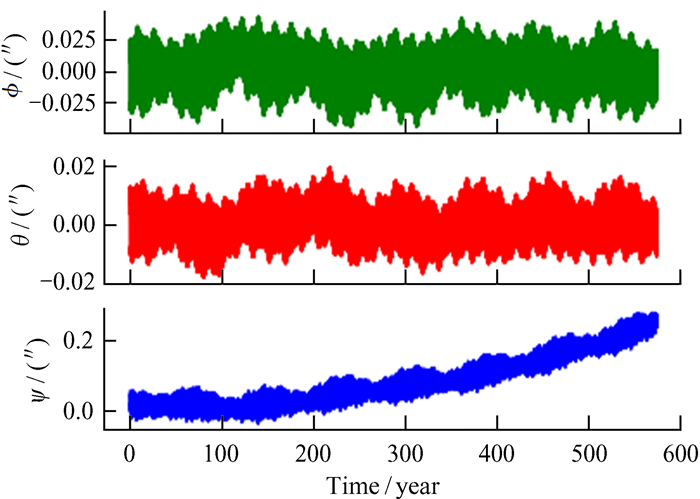
1 月球转动欧拉角月球历表中包含各个天体在国际天球坐标系中的位置和速度状态信息,还包含月球的转动欧拉角。利用INPOP19a,INPOP17a和DE430历表中跨度600年的数据提取得到的欧拉角比较如图 1~图 3。
|
| 图 1 INPOP19a与INPOP17a欧拉角的差别 Fig. 1 The difference of Euler angle between INPOP19a and INPOP17a |
|
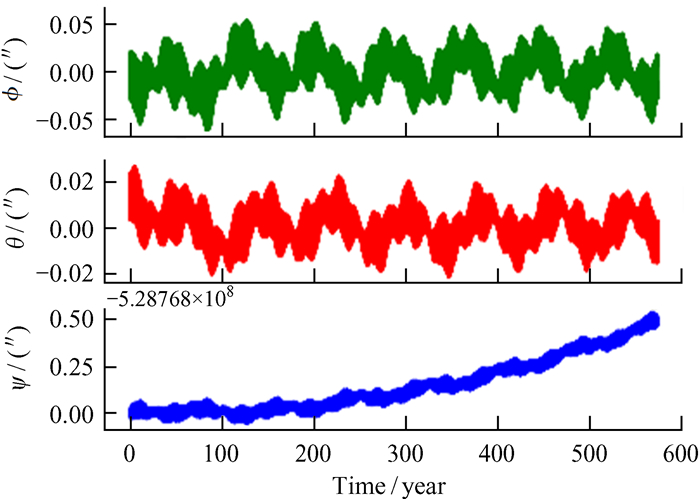
| 图 2 INPOP17a与DE430欧拉角的差别 Fig. 2 The difference of Euler angle between INPOP17a and DE430 |
|
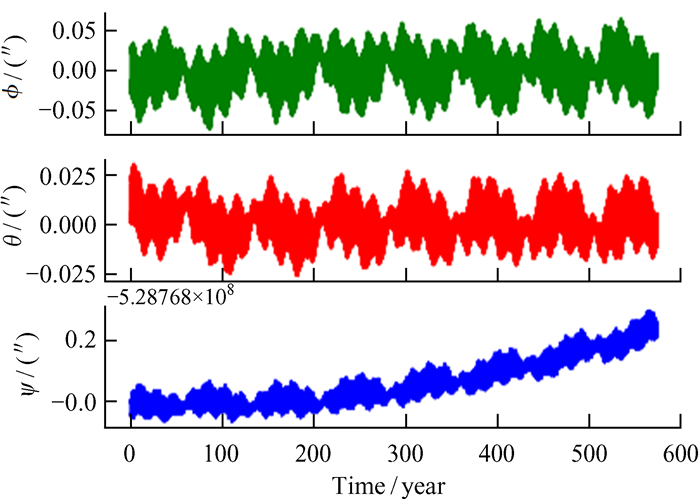
| 图 3 INPOP19a与DE430欧拉角的差别 Fig. 3 The difference of Euler angle between INPOP19a and DE430 |
由图 1~图 3可知,INPOP17a与DE430欧拉角差别较大,INPOP19a更为稳定。其中,ϕ和θ在不同历表中相差0.05″左右。但是ψ随着时间逐渐增大,说明历表中ψ的拟合模型不稳定。对比历表欧拉角的差别,计算的地心到月面反射器A15的距离最大误差有30 cm,对月球激光测距的预报精度有较大的影响。
以上完成了对天平动欧拉角的提取,利用快速傅里叶变换算法对提取的欧拉角之差进行了频谱分析,结果如表 1。27.3天是极位置在惯性坐标系下自由天平动的周期。
| INPOP19a-DE430 | INPOP19a-INPOP17a | INPOP17a-DE430 | |
| ϕ | 27.3 | 27.32 | 27.3 |
| θ | 27.3 | 27.32 | 27.3 |
| ψ | 27.3 | 27.32 | 27.3 |
月球天平动是指地面观测者所观测的月球可见面上下左右小幅度的摆动。由于天平动效应,观测者能看到69%的月面,其中有19%时多时少。
月球相对于地心的月面经度天平动和纬度天平动称为光学天平动或几何天平动。几何天平动中的经度项和纬度项除了与月球本身的物理天平动有关,还与月球的公转轨道密切相关。月球实际摆动形成的天平动称为物理天平动,物理天平动是月球自身相对于空间坐标的转动欧拉角,与月球的内部结构、自转动量和转动惯量有关。本文具体实现从历表获得的欧拉角到月球物理天平动的转换过程。
月固坐标系分为月球主轴坐标系(Principal Axis Frame, PA)与平均地球指向坐标系(Mean Earth, ME)。在描述月球转动时,我们以月球质心为原点,月球3个惯量主轴为3个坐标轴,建立随月球转动的月球主轴坐标系。同时,我们可以得到坐标指向与国际天球参考系(International Celestial Reference System, ICRS) 一致的月心天球参考系。两个坐标系通过3个欧拉角ϕ,θ和ψ进行转换:
| $ [I C R S]=\boldsymbol{R}_{z}(-\phi) \cdot \boldsymbol{R}_{\mathrm{x}}(-\theta) \cdot \boldsymbol{R}_{z}(-\psi) \cdot[P A]. $ | (1) |
这3个与月球转动相关的欧拉角及变化率即月球天平动的数值表达,反映月球自转的状态。依据卡西尼定则:(1) 月球自转周期等于公转周期;(2) 月球赤道与黄道的夹角为1 °32′;(3) 月球自转轴、月球轨道平面的法线以及黄道面的法线三者共面,且第三者处于前两者之间。月球物理天平动的理论基础主要是刚体转动微分方程,由卡西尼第一定律(月球自转周期等于公转周期) 简化得到,对于刚体月球转动微分方程为经典的欧拉-刘维尔方程
| $ \frac{\mathrm{d}(I \boldsymbol{\omega})}{\mathrm{d} t}+\boldsymbol{\omega} \times I \boldsymbol{\omega}=\boldsymbol{T}, $ | (2) |
其中,ω代表月球的转动角速度;T为月球受到的摄动力。我们可以直接从DE历表读取月心天球参考系到月球主轴坐标系的转换矩阵。欧拉角从惯性参考系转换到旋转坐标系时,
| $ \boldsymbol{R}_{x}=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & \sin \alpha \\ 0 & -\sin \alpha & \cos \alpha \end{array}\right], $ | (3) |
| $ \boldsymbol{R}_{y}=\left[\begin{array}{ccc} \cos \phi & 0 & -\sin \phi \\ 0 & 1 & 0 \\ \sin \phi & 0 & \cos \phi \end{array}\right], $ | (4) |
| $ \boldsymbol{R}_{z}=\left[\begin{array}{ccc} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{array}\right]. $ | (5) |
此转换过程可用公式
| $ \begin{aligned} {[ { ICRS }] } &=\boldsymbol{R}_{z}(-\varphi) \boldsymbol{R}_{x}(-\theta) \boldsymbol{R}_{z}(-\psi)[P A] \\ &=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \phi & \sin \phi \\ 0 & -\sin \phi & \cos \phi \end{array}\right]\left[\begin{array}{ccc} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \psi & \sin \psi \\ 0 & -\sin \psi & \cos \psi \end{array}\right][P A] \\ &=\left[\begin{array}{ccc} \cos \theta \cos \psi & \cos \theta \sin \psi & -\sin \theta \\ -\cos \phi \sin \psi+\sin \phi \sin \theta \cos \psi & \cos \phi \cos \psi+\sin \phi \sin \theta \sin \psi & \sin \phi \cos \theta \\ \sin \phi \sin \psi+\sin \phi \sin \theta \cos \psi & -\sin \phi \cos \psi+\cos \phi \sin \theta \sin \psi & \cos \phi \cos \theta \end{array}\right][P A] \end{aligned} $ | (6) |
表示。(6) 式是月心天球参考系到月球主轴坐标系转换的理论基础。将这一向量转换到瞬时黄道坐标系,有
| $ r^{\text {date }}=\boldsymbol{R}_{x}(\varepsilon) \boldsymbol{B} \boldsymbol{N P}[ { ICRS }], $ | (7) |
其中,B, N和P分别为坐标偏差矩阵、岁差矩阵和章动矩阵;ε为瞬时真黄道坐标系的旋转。
将月球主轴坐标系中的单位向量R1=(1, 0, 0)和R2=(0, 0, 1) 通过上述坐标转换至瞬时黄道坐标系,得到Xdate和Zdate。i, j和k分别为在黄道坐标系下沿着Ox,Oy和Oz的单位向量。n为坐标原点指向月球赤道与黄道的升交点的单位向量,此时有
| $ \boldsymbol{n}=\frac{z^{\text {date }} \times k}{\left|z^{\text {date }} \times k\right|}. $ | (8) |
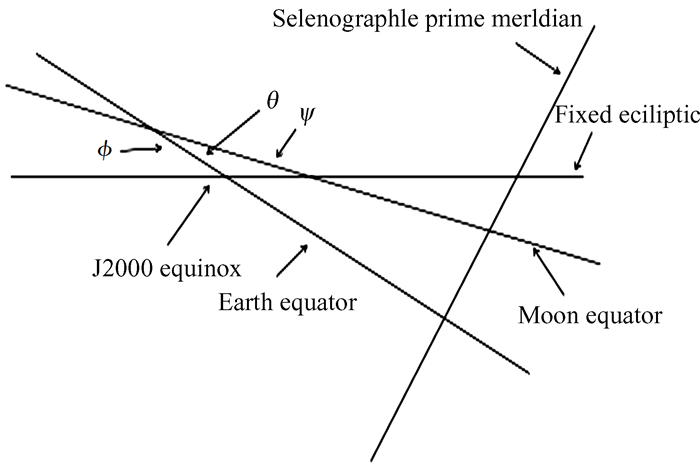
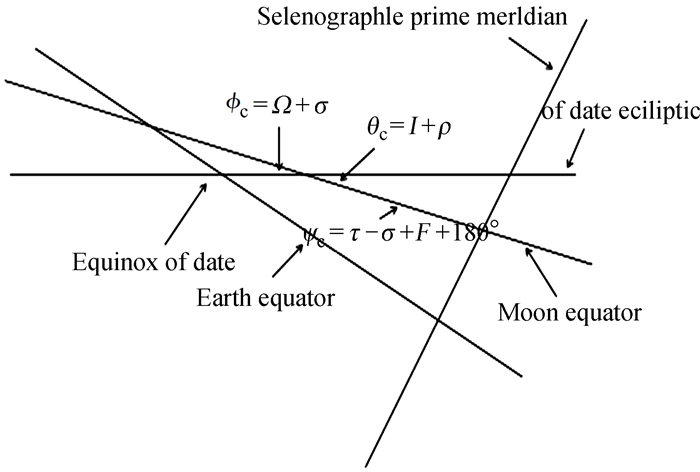
利用图 4与图 5中各量的关系,可以得到ϕc, θc和ψc:
| $ \begin{gathered} \cos \phi_{\mathrm{c}}=\boldsymbol{i} \cdot \boldsymbol{n}, \end{gathered} $ | (9) |
| $ \sin \phi_{\mathrm{c}}=\boldsymbol{j} \cdot \boldsymbol{n}, $ | (10) |
| $ \cos \theta_{\mathrm{c}}=\boldsymbol{k} \cdot z^{\mathrm{date}}, $ | (11) |
| $ \cos \psi_{\mathrm{c}}=\boldsymbol{n} \cdot z^{\mathrm{date}}, $ | (12) |
| $ \sin \psi_{\mathrm{c}}=\left(z^{\mathrm{date}} \times \boldsymbol{n}\right) \cdot x^{\mathrm{date}} . $ | (13) |
根据Newhall[1]研究中使用的公式,我们可以得到
| $ \phi_{\mathrm{c}}={\mathit{\Omega}}+\sigma, $ | (14) |
| $ \theta_{\mathrm{c}}=I+\rho, $ | (15) |
| $ \psi_{\mathrm{c}}=\tau-\sigma+F+180^{\circ} . $ | (16) |
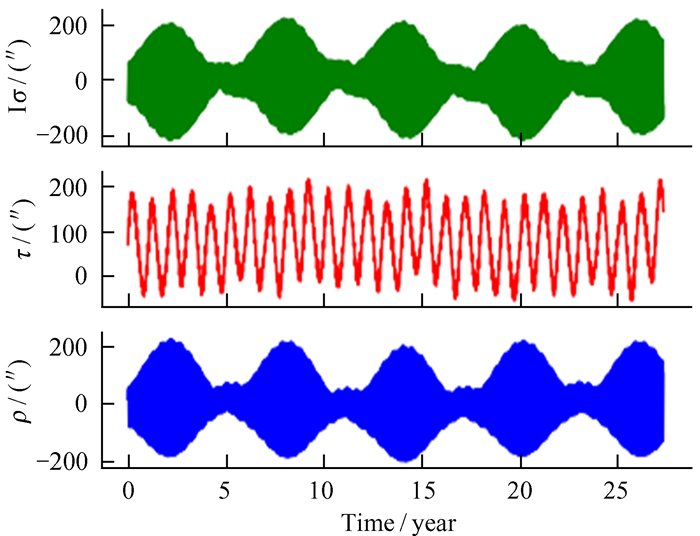
在上述过程中,我们把图 4赤道坐标系下的欧拉角ψ,θ和ϕ转换为图 5黄道坐标系下的ϕc,θc和ψc。Eckhardt分别使用Ισ,ρ和τ表示天平动中的周期项。其中,ρ是由θc分离出来,定义为解的周期部分,θc由(15) 式定义,I是一个线性多项式。根据(14) 式,Ω是轨道节点的经度,σ是两个节点之间的瞬时差,将(14) 式变为Ιϕc=ΙΩ+Ισ,Ισ定义为由一个常数和解的周期部分组成。同时(16) 式可以变化为ψc+ϕc=τ+Ω+F+180 °,定义τ由一个常数和结果的周期部分组成。我们分别使用Ισ,τ和ρ表示月球的物理天平动,根据上述过程计算得到结果最终如图 6。
|
| 图 4 月球主轴坐标系到国际天球参考系中的旋转欧拉角 Fig. 4 Rotated Euler angle from PA coordinate system to ICRS |
|
| 图 5 月球主轴坐标系到黄道坐标系的欧拉角 Fig. 5 Euler angle from PA coordinate system to ecliptic coordinate system |
|
| 图 6 利用INPOP19a历表实现对月球物理天平动的提取 Fig. 6 Using INPOP19a ephemeris to extract the lunar physical librations |
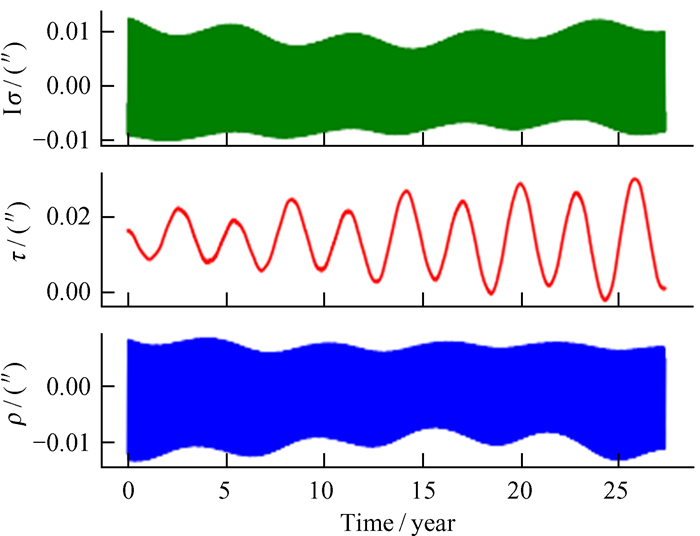
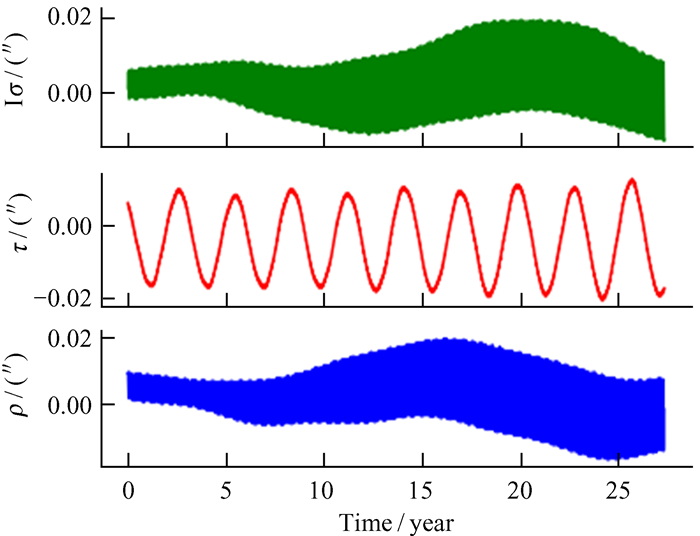
至此完成了利用数值历表中欧拉角对物理天平动的转换。利用上述方法,从INPOP17a与DE430中分别提取物理天平动与INPOP19a作差比较,结果如图 7和图 8。结果显示,INPOP19a与INPOP17a物理天平动差别更为稳定。
|
| 图 7 INPOP19a与INPOP17a物理天平动差别 Fig. 7 The difference between INPOP19a and INPOP17a |
|
| 图 8 INPOP19a与DE430物理天平动差别 Fig. 8 The difference between INPOP19a and DE430 |
由图 6物理量τ绘制的图与图 7中INPOP19a与INPOP17a之差对比,我们发现存在一个稳定频率的周期,且此频率与τ本身的固有频率不同,故在研究过程中重点对此频率进行分析。
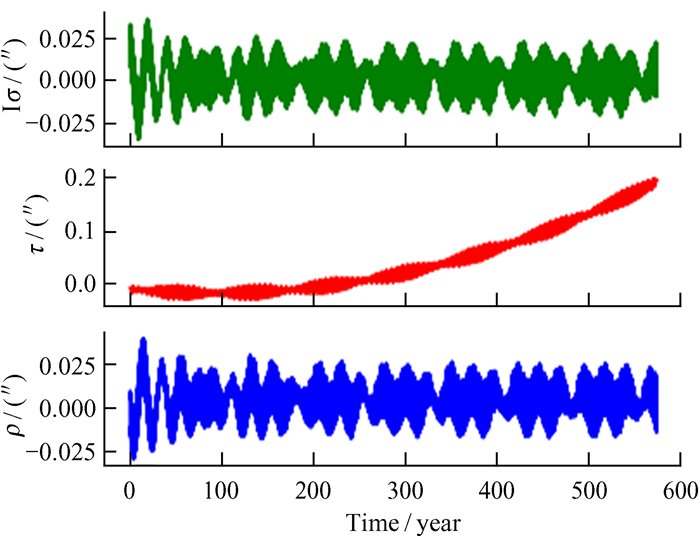
首先,根据上述过程,利用INPOP19a,INPOP17a和DE430历表中跨度600年的数据提取得到的物理天平动比较如图 9~图 11。
|
| 图 9 INPOP17a与DE430物理天平动的差别 Fig. 9 The difference of physical librations between DE430 and INPOP17a |
|
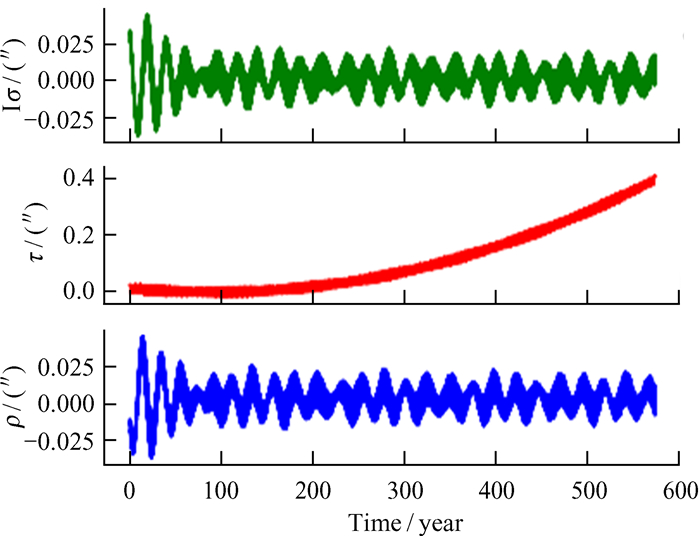
| 图 10 INPOP19a与DE430物理天平动的差别 Fig. 10 The difference of physical librations between INPOP19a and DE430 |
|
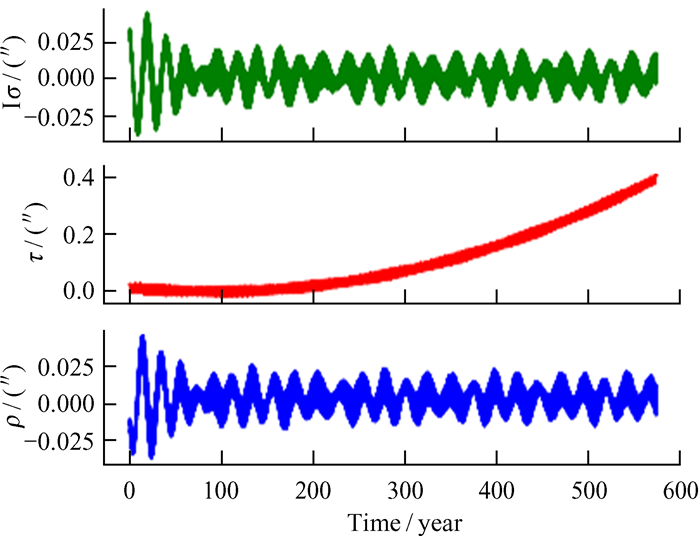
| 图 11 INPOP19a与INPOP17a物理天平动的差别 Fig. 11 The difference of physical librations between INPOP17a and INPOP19a |
我们利用快速傅里叶变换算法对上面的图像进行频谱分析,结果如表 2。
| INPOP19a-INPOP17a | INPOP19a-DE430 | INPOP17a-DE430 | |
| Ισ | 27.21 | 27.18 | 27.18 |
| τ | 1 056.53 | 1 056.53 | 1 056.53 |
| ρ | 27.21 | 27.18 | 27.18 |
| 其中,1 056.53天的周期是经度方向的自由天平动周期,27.21天和27.18天则是物理天平动中F模型和Wobble模型引起的。 | |||
本文利用已有的数值历表数据开展月球物理天平动研究,得到INPOP19a历表中3个欧拉角的相位时间图像,与INPOP17a,DE430历表进行对比,发现其差值存在27.3天的周期,识别出了极位置在惯性坐标系下的自由天平动。本文进一步利用历表数据对月球天平动进行分析,根据卡西尼定则以及国际天球参考系到月球主轴坐标系的转换模型,提取得到月球相对于空间的摆动即月球的物理天平动。结果显示,月球的物理天平动存在一定的周期,但振幅在200毫角秒内,与我们能看到69%的月面相比,是一个极其微小的摆动量。即在地球上观测月球的天平动时,月球的几何天平动为主要影响因素。3个历表提取得到的物理天平动作差比较,发现存在一个稳定周期,且此周期与固有周期不同,频谱分析以后将3个不同历表得到的周期进行了比较。
本文对提取得到的欧拉角进行分析,计算得到新一代数值历表INPOP19a与DE430,INPOP17a提取得到的欧拉角换算到月球激光测距上最多有30 cm的误差。此误差对月球激光测距的预报精度产生较大的影响。与DE430,INPOP17a相比,INPOP19a有较高的稳定性,故在月球激光测距或者研究物理天平动时,推荐采用历表INPOP19a。
| [1] | NEWHALL X X, WILLIAMS J G. Estimation of the lunar physical librations[J]. Celestial Mechanics and Dynamical Astronomy, 1997, 66(1): 21–30. DOI: 10.1007/BF00048820 |
| [2] | QI Y, RUITER A D. Transfers to lunar libration point orbits[J]. Communications in Nonlinear Science and Numerical Simulation, 2019, 74: 180–200. DOI: 10.1016/j.cnsns.2019.01.033 |
| [3] | PETROVA N K, NEFEDYEV Y A, ZAGIDULLIN A A, et al. Use of an analytical theory for the physical libration of the Moon to detect free nutation of the lunar core[J]. Astronomy Reports, 2018, 62(12): 1021–1025. DOI: 10.1134/S1063772918120120 |
| [4] | YANG Y Z, LI J L, PING J S, et al. Determination of the free lunar libration modes from ephemeris DE430[J]. Research in Astronomy and Astrophysics, 2017, 17(12): 91–96. |
| [5] | YANG Y Z, PING J S, YAN J G, et al. Comparison and analysis on lunar rotation with lunar gravity field models[J]. Astrophysics and Space Science, 2018, 363(9): 190. DOI: 10.1007/s10509-018-3413-z |
| [6] | YANG Y Z, HE Q B, PING J S, et al. Estimation of the lunar free libration modes based on the recent ephemerides[J]. Astrophysics and Space Science, 2019, 364(12): 218. DOI: 10.1007/s10509-019-3684-z |
| [7] |
李金岭, 聂昭明, 金文敬. 用激光测月法测定月球自由天平动[J]. 科学通报, 1989(22): 1718–1720 LI J L, NIE Z M, JIN W J. Measuring the free libration of the Moon by laser lunar ranging[J]. Chinese Science Bulletin, 1989(22): 1718–1720. |
| [8] |
李广宇, 田兰兰. PMOE2003行星历表框架(V)历表文件的生成和使用[J]. 紫金山天文台台刊, 2004(Suppl 1): 160–170 LI G Y, TIAN L L. PMOE2003 planetary ephemeris framework (V) creating and using of ephemeris files[J]. Publications of Purple Mountain Observatory, 2004(Suppl 1): 160–170. |
| [9] |
李语强, 伏红林, 李荣旺, 等. 云南天文台月球激光测距研究与实验[J]. 中国激光, 2019, 46(1): 188–195 LI Y Q, FU H L, LI R W, et al. Research and experiment of lunar laser ranging at Yunnan Observatories[J]. Chinese Journal of Lasers, 2019, 46(1): 188–195. |


