耀变体的多波段光变时标是一个重要的物理参数，耀变体的长周期光变时标可以帮助我们研究天体的中心黑洞质量、内部结构和辐射区域等问题。目前研究此类问题的方法很多，有结构函数法、离散相关函数法(Discrete Correlation Function, DCF)、period4方法、功率谱(Power Spectral Density, PSD)、Jurkevich方法、加权小波Z变换法(Weighted Wavelet Z-transform, WWZ) ^[1]和LSP方法^[2]等。由于天体光学波段和红外波段的观测受天气、设备等多种因素的影响，观测数据在时间序列上不连续, 在光变周期的研究中引入较大的误差, 结果的精确度一直是该研究领域的热点问题。文[3]对这个天体光学和红外波段的数据采用功率谱分析方法，得到了与本文相同的结果，但是在功率谱方法中要求数据为等间隔，所以文[3]对相邻的数据进行了平均插值处理，这样可能损害了原始数据的真实性，引入人为因素，还可能带来其他叠加对周期的干扰。本文从SMARTS和文[3]中收集了耀变体3C 454.3^[3]近10年光学波段的准同时性数据，利用LSP方法对耀变体3C 454.3的非均匀数据进行分析。LSP方法不需要对数据进行插值，但是在功率谱结果中可能出现虚假的峰值。为了进一步评估功率谱峰值的可信度，通过模拟大量光变曲线，并采用LSP方法计算模拟光变曲线的功率谱，对模拟光变曲线的功率谱结果进行抽样，估计相应波段的置信度。通过置信度评估所出现峰值的可靠性，我们可以得出更为准确的准周期，并且在分析结果中得到的周期只有一个，而没有其他的干扰周期，这种模拟大量光变曲线的方法称为蒙特卡洛模拟方法。为了验证蒙特卡洛模拟方法的可行性和结果的准确性，我们根据5个波段的数据，利用加权小波Z变换方法进行长周期光变分析，也得到相同的结果，并通过文[4]中的标准差公式计算相应波段的置信度，得出了可靠的准周期, 从而验证了蒙特卡洛模拟方法的可行性和结果的准确性。本文首次将耀变体3C 454.3光学B，V，R波段和红外J，K波段的离散数据应用加权小波Z变换法和蒙特卡洛模拟方法来研究相应波段的光变周期，为耀变体的长周期光变研究找到了一种新方法，通过加权小波Z变换法和蒙特卡洛模拟方法可以得到非平稳信号的准周期，大大提高了周期的计算精度，从而得到更加准确的准周期。我们使用这两种方法得到5个波段都存在约454天的准光变周期。从长周期的研究中我们可以得到3C 454.3中心黑洞质量和辐射区半径，从而为活动星系核(Active Galactic Nucleus, AGN) 物理模型的研究提供重要参数。

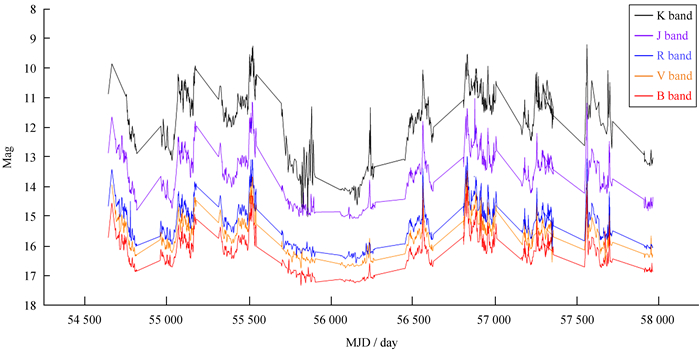
1 观测数据和研究

由SMARTS数据库和文[3]中耀变体3C 454.3光学B，R，V波段和红外J，K波段的数据得到的光变曲线如图 1，横轴为儒略日(MJD)，纵轴为星等值(Mag)。

根据流量与星等的转化关系, 5个波段的星等转化为流量的公式为^[5]

$ F=10^{-\frac{m}{2.5}} \times 3640 \mathrm{Jy}, $

(1)

其中，F为每个波段对应的流量值，单位为Jy；m为对应波段的星等值。

1.1 光变曲线的长周期分析

从SMARTS数据库和文[3]获得星等的数据之后，通过流量与星等的转化公式得到各个波段的流量数据。接下来本文采用蒙特卡洛模拟^[6]和加权小波Z变换法计算各个波段的周期和各自的置信度。即用图 1的光变曲线获得流量数据后，利用LSP方法得到相应的光变周期和蒙特卡洛模拟方法得到相应的置信度估计。为了检验蒙特卡洛模拟方法置信度评估的可行性和结果的准确性，我们通过加权小波Z变换法计算相应波段的光变周期，通过标准差公式，我们计算了相应的加权小波Z变换周期的置信度。

1.2 LSP方法分析长周期光变

计算隐藏在噪声中的周期信号是天文数据时间序列分析中的一个重要目标。LSP方法可以对非均匀采样的时间序列周期图进行相位修正处理，能够在一定范围内对非均匀采样的时间间隔引起的误报周期进行修正，并且LSP方法不要求数据是均匀的时间序列，不用对其进行插值，从而减少了人为因素对数据的干扰。因此，LSP方法能寻找隐藏在噪声中的准周期振荡光变。现在假定一组时间序列x(t_j)，(j=1, 2, 3, …, N)，则时间序列的LSP功率谱为

$ P_{x}\left(\omega_{j}\right)=\frac{1}{2}\left\{\frac{\sum\limits_{j=1}^{N}\left[x\left(t_{j}\right)-\bar{x}\right] \cos \omega_{j}\left(t_{j}-\tau\right)}{\sum\limits_{j=1}^{N} \cos ^{2} \omega_{j}\left(t_{j}-\tau\right)}+\frac{\sum\limits_{j=1}^{N}\left[x\left(t_{j}\right)-\bar{x}\right] \sin \omega_{j}\left(t_{j}-\tau\right)}{\sum\limits_{j=1}^{N} \sin ^{2} \omega_{j}\left(t_{j}-\tau\right)}\right\}, $

(2)

其中，P_x(ω_j) 是以角频率(ω_j=2πν_j) 为变量的功率谱函数；$\bar{x}=\frac{1}{N} \sum\limits_{j=1}^{N} x\left(t_{j}\right)$为时间序列的平均值；N为数据的个数；τ为相应的时间相位修正，

$ \tan \left(2 \omega_{j} \tau\right)=\frac{\sum\limits_{j=1}^{N} \sin ^{2} \omega_{j} t_{j}}{\sum\limits_{j=1}^{N} \cos ^{2} \omega_{j} t_{j}}. $

(3)

图 1的光变曲线是一个非均匀的时间序列，要得到隐藏在其中的真实周期非常困难。我们利用LSP方法分析真实数据的功率谱结果，但是由于这些结果中出现虚假峰值，很难判别真实的周期频率，所以为了解决这个问题，我们需要对这些功率谱的峰值进行置信度评估。

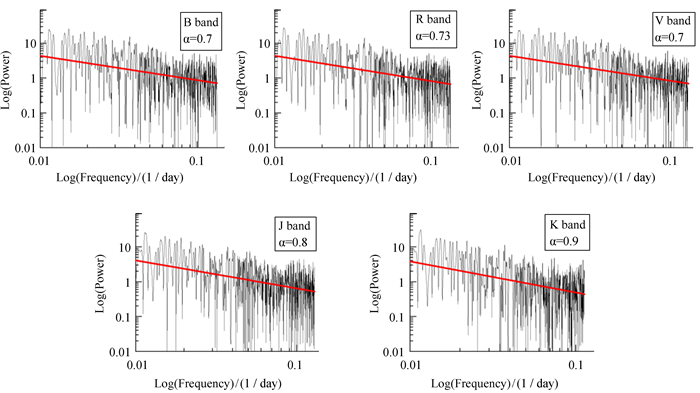
1.3 蒙特卡洛模拟方法和置信度评估

活动星系核的功率谱一般呈红噪声幂律分布^[6]，即P∝f^-α，为了获得功率谱指数α，对所得到的功率谱结果取对数, 并进行一元线性回归拟合，可以获得功率谱指数α。光学B，R，V波段和红外J，K波段的功率谱对数坐标拟合结果如图 2。

图 2中的横坐标是频率f的对数，纵坐标为功率谱的对数，红色直线为相应的一元线性拟合结果，图中直线的斜率为功率谱指数α。通过一元线性回归拟合，我们得到光学和红外波段的各个幂律指数α。基于功率谱指数α和真实数据，我们模拟了5 000条光变曲线，对模拟的光变曲线利用LSP方法逐一进行计算，获得模拟光变曲线的功率谱结果，对这些模拟光变曲线的功率谱进行置信度抽样，得到各个波段不同的置信度曲线，最终将真实数据的功率谱和置信度曲线整合，即可得到准确的周期频率。

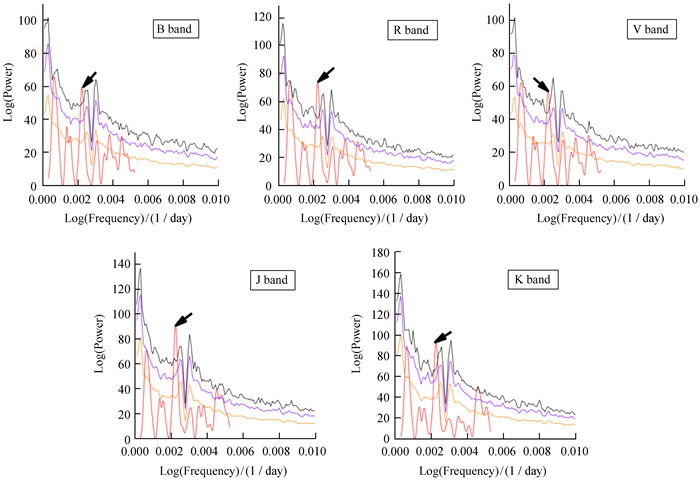
1.4 LSP方法的置信度评估结果

光学B，R，V波段和红外J，K波段的置信度评估结果如图 3。图 3分别为各波段的蒙特卡洛模拟LSP方法结果，横坐标为频率f的对数，纵坐标为相应波段功率谱的对数，红色曲线代表真实数据的功率谱结果，黑色曲线代表置信度为99.7%，紫色曲线代表置信度为99%，橙色曲线代表置信度为95%。我们取超过置信度99.7%的峰值为所对应的周期频率，如图中黑色箭头所指的位置。

由图 3我们看到，在光学B，R，V波段和红外J，K波段只存在一个很明显的峰值超过99.7%，如图 3中箭头所指的位置，相应的峰值频率保留4位小数都为f=0.002 2 (d^-1)，所以光学和红外波段都存在约454天的周期。通过这种方法我们得到了与文[3]相同的结果，并且这种方法不会引入其他干扰因素。为了检验以上方法的可行性和结果的准确性，我们通过加权小波Z变换法^[1]计算相应波段的周期。由于标准差和置信度的关系，我们计算了相应的加权小波Z变换功率谱的置信度，本文采用文[4]给出的正态分布标准差公式。

2 加权小波Z变换法分析长周期光变

经典的时间频率分析一般采用傅里叶变换和小波分析方法，但是由于天文数据往往是非等间距的离散数据，在使用傅里叶变换和小波变换分析时，我们需要对数据进行插值变成均匀的数据，这样损害了数据的真实性，在使用傅里叶变换处理这些非等间隔数据时可能出现伪周期，所以在小波变换的基础上文[1]提出了加权小波Z变换法，不仅可以更加有效地处理非等间隔的时间序列的周期，还可以一定程度上反映周期的稳定性。加权小波Z变换是将时间序列投影到3个正交归一的基函数上，即ϕ₁(t_i)= 1, ϕ₂(t_i)= cos[ω(t-τ₀)]和ϕ₃(t_i)= sin[ω(t-τ₀)]，在投影上做统计加权ω_i =exp[-cω²(t_i-τ₀)]，将不均匀的数据通过权重调节，避免周期分析时受到数据过密的影响，其中使用的母函数为Morlet小波^[1]。加权小波Z变换的定义为

$ WWZ = \frac{{\left( {{N_{{\rm{eff }}}} - 3} \right){V_{\rm{y}}}}}{{2\left( {{V_{\rm{x}}} - {V_{\rm{y}}}} \right)}}, $

(4)

这个等式的分子分母分别满足自由度为N_eff-3和2的F分布。其中，N_eff为有效数据点个数；V_x和V_y分别为观测数据和模拟函数的加权变量，即

$ N_{\mathrm{eff}} =\frac{\left\{\sum \exp \left[-2 c \omega^{2}\left(t_{i}-\tau_{0}\right)^{2}\right]\right\}^{2}}{\sum \exp \left[-2 c \omega^{2}\left(t_{i}-\tau_{0}\right)^{2}\right]}, $

(5)

$ V_{\mathrm{x}} =\frac{\sum\limits_{i} \omega_{i} x^{2}\left(t_{i}\right)}{\sum\limits_{\lambda} \omega_{\lambda}}-\left[\frac{\sum\limits_{i} \omega_{i} x^{2}\left(t_{i}\right)}{\sum\limits_{\lambda} \omega_{\lambda}}\right]^{2} , $

(6)

$ V_{\mathrm{y}} =\frac{\sum\limits_{i} \omega_{i} y^{2}\left(t_{i}\right)}{\sum\limits_{\lambda} \omega_{\lambda}}-\left[\frac{\sum\limits_{i} \omega_{i} y^{2}\left(t_{i}\right)}{\sum\limits_{\lambda} \omega_{\lambda}}\right]^{2}. $

(7)

其中，c为衰减因子；τ₀为时移；ω为尺度因子；ω_λ (λ=1, 2, 3, …, n)为对应的测试频率。

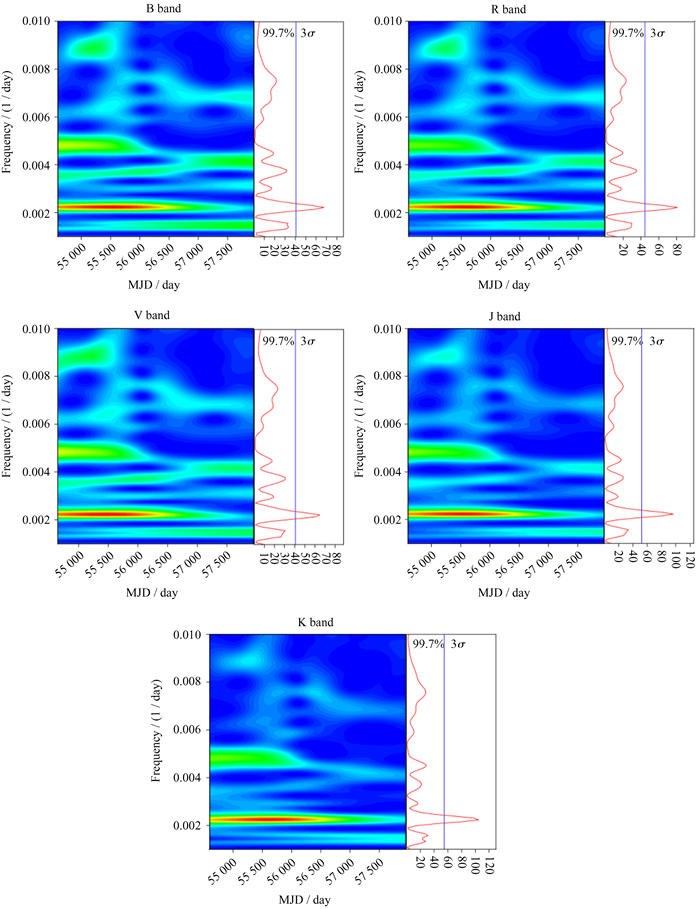
光学B，R，V波段和红外J，K波段的加权小波Z变换法分析结果和相应的周期频率如图 4。从图 4可以看出，在光学B，R，V波段和红外J，K波段左边彩图红色部分对应右图的功率谱曲线，峰值频率的位置为相应的周期频率出现的位置，通过白噪声检验采用^[4]，$\sigma=\left(\sum\limits_{i=1}^{M} \delta_{i}^{2} / M-1\right)^{\frac{1}{2}}$对于正态分布总体成立，等式中δ_i=m_i-m为相应波段的每一个功率值(m为相应波段功率的平均值)，M为离散功率谱个数。通过计算各个波段功率谱的标准差，由于正态分布置信度与标准差的关系，我们可以获得各个波段功率谱的置信度，采用3倍标准差所对应的置信度99.7%，所以图 4中右图的蓝色直线取3倍标准差。通过以上计算，各个波段周期频率都出现在f=0.002 2 (d^-1) 处，所以光学和红外波段都存在约454天的周期，并且置信度超过99.7%，这个结果与蒙特卡洛模拟LSP方法的结果一致。综上我们得到了耀变体3C 454.3在光学B，R，V波段和红外J，K波段的周期都为454天，大约1.244年。

3 3C 454.3中心黑洞质量和辐射区域半径的估计 3.1 中心黑洞质量

耀变体中心有一个超大质量黑洞，很多辐射现象是由中心黑洞引起。通过长时标光变能够获得中心黑洞的质量，假设由薄吸积盘理论引起的长周期光变的公式为^[7]

$ t_{\text {burts }}=4.52 \beta_{0.1}^{-0.62} M_{6}^{1.37} \text { year , } $

(8)

其中，β为黏度参数；M₆=M/(10⁶M_⊙) 为中心黑洞质量约化单位。吸积率$\dot M$和广义应力张量参数μ，当μ=0.5时，$\dot M$=M_E/ε，M_E为爱丁顿吸积率，ε为吸积效率。爆发时间间隔主要取决于μ。文[7]建议μ=0.5时，磁场的逃逸速率更低。此时, 热极限周期时间为t_cyc=2t_burts，

$ t_{\text {cyc }}=9.0 \beta_{0.1}^{-0.62} M_{6}^{1.37} \text { year }, $

(9)

其中，β_0.1=β/0.1，所以当β=0.1，μ=0.5，$\dot{M}=0.2 \dot{M}_{C}$时，我们采用5个波段1.244年的周期得到中心黑洞的质量约为M≈0.24×10⁶M_⊙。由于利用薄吸积盘理论的分析方法得到这个结果，没有考虑黑洞自旋的影响，所以比一般的平谱射电类星体的中心黑洞质量偏小。

3.2 辐射区半径

对于耀变体的长周期光变现象，目前还没有最佳的物理模型解释，现有的理论为双黑洞模型^[8]、薄盘的热不稳定性模型^[8]和螺旋喷流等模型^[9-10]。如果是薄盘不稳定性造成的，从搜集的数据中获得各个波段的星等变化情况如表 1。

由表 1可以看出，耀变体3C 454.3在光学和红外波段都具有较为剧烈的变化，并且红外波段的变化幅度比光学波段更加剧烈。采用薄盘不稳定性分析长周期T^[8]，通过长周期T可以确定热不稳定性产生的区域，公式为

$ T=3.2 \times 10^{-4} \beta^{2}\left[x^{\frac{1}{2}}(x-1) M_{8}\right] \text { year , } $

(10)

其中，x=R/R_g，R_g为施瓦西半径；β为黏滞系数；M₈=M/(10⁸M_⊙)。这里我们取T≈1.244 year，中心天体黑洞质量为M≈0.24×10⁶ M_⊙，所以我们得到辐射区域半径为R≈3.68×10⁸ km。

4 结果

对耀变体3C 454.3光学波段和红外波段的研究中，本文采用LSP方法得到了各个波段的周期，评估了峰值频率的置信度，得到更为可靠的结果，并采用加权小波Z变换法验证蒙特卡洛模拟评估置信度方法的结果，我们发现：

(1) 两种方法都在光学B，R，V波段和红外J，K波段发现454天，约1.244年的光变周期，通过蒙特卡洛模拟评估置信度方法，我们清楚地看到对于5个波段都只有一个峰值频率超过99.7%，并且没有引入其他干扰结果。为了进一步验证这种方法的可行性，我们对5个波段采用加权小波Z变换的分析方法，也得到了与蒙特卡洛模拟方法一致的结果，都为454天，约1.244年。

(2) 对于中心的超大质量黑洞，通过文献给出的长周期与黑洞质量的公式，结合本文中5个波段共同的长周期数据，我们得到中心黑洞的质量为M≈0.24×10⁶ M_⊙。由于这个结果是利用薄吸积盘理论的分析方法，没有考虑黑洞自旋的影响，所以比一般平谱射电类星体的中心黑洞质量偏小，辐射区半径为R≈3.68×10⁸ km，计算得到的辐射区半径比文[11]给出的辐射区半径在相应的施瓦西半径下要小，由于文[11]采用的黑洞质量比本文中所用的黑洞质量大，所以此处我们得到的辐射区半径是合理的。

(3) 通过以上的计算，我们预测耀变体3C 454.3在2021年6月左右将再次爆发。我们将用云南天文台丽江观测站2.4 m光学望远镜做进一步实测验证，为蒙特卡洛模拟方法研究耀变体的长周期光变寻求观测证据。

致谢: 真诚致谢SMARTS团队和吴月承等人在文[3] 中提供的光学和红外波段的星等数据。