2. 暨南大学中法天体测量、动力学与空间科学联合实验室, 广东 广州 510632
2. Sino-French Joint Laboratory for Astrometry, Dynamics and Space Science, Jinan University, Guangzhou 510632, China
信息化与工业化是社会与科技发展的必然趋势。目前,科研工作者在天体测量数据的处理和研究中使用的工具和软件不同,这在一定程度上不利于对科学的讨论与探究。CCD图像处理是天体测量中一个重要的环节,正确地使用现有的天体测量处理工具和软件可以确保图像处理结果的准确性和可信性,也有利于推动科学研究的探索和发展。
Astrometrica[1]和MaxIm DL[2]是两个可用于天体测量的开源软件。当然,也有许多科研工作者使用自主研发的处理程序和软件,如文[3]开发的射电测量集文件生成软件和文[4]的一维光谱可视化与分析工具。本文主要对Astrometrica和MaxIm DL在天体测量中的应用和处理结果进行比较和技术研究。Astrometrica是由Raab Herbert研发的用于天体测量数据处理的软件,对于太阳系小行星巡天、数据归算有较大的帮助和参考价值,主要有CCD图像的读写与变换、平场校正、太阳系小行星目标检测、数据归算、图像堆叠等功能,为天体测量、巡天等提供参考并取得了良好的进展。例如,文[5]使用Astrometrica对土星卫星CCD图像进行处理与位置测量,准确度较高;文[6]使用该软件进行巡天工作,发现了280颗近地小行星。MaxIm DL是由Diffraction公司研发的主要用于天文望远镜观测、测光和天体测量的软件,文[7]使用MaxIm DL对OJ 287天体的观测资料进行平场处理和测光的数据处理。
1 Astrometrica与MaxIm DL的应用比较与技术研究Astrometrica主要有CCD图像的读写与变换、平场校正、太阳系小行星移动目标检测、数据归算、图像堆叠、生成报告等功能,对太阳系巡天与天体测量有较大的帮助。MaxIm DL主要有控制观测设备、读写CCD图像、测光、图像质量评估、图像堆叠、运行自定义脚本等功能。虽然MaxIm DL也能进行相应的数据归算,但是该功能需要协同其他软件才能使用,所以本文不讨论两个软件数据归算功能的比较,相比之下,MaxIm DL的功能要比Astrometrica的多。本文主要从两个软件用于天体测量的功能进行比较与技术研究。具体地,从CCD图像的读写与变换、平场校正、Astrometrica参数的设置与归算、图像堆叠和两个软件的总体评价进行详细论述。
1.1 CCD图像的读写与变换在图像的读写过程中,Astrometrica可以读取8位、16位和32位的整型普适图像传输系统(Flexible Image Transport System)图像,但只能存储为16位的整型图像;MaxIm DL支持更多图像格式的读取与存储,具体可以查阅该产品的用户手册。值得注意的是,两个软件目前还不支持64位浮点型FITS图像的读取,但SAOImage DS9[8]支持。如果用Astrometrica和MaxIm DL进行图像处理,需要尽量避免使用FITS图像。Astrometrica,MaxIm DL和SAOImage DS9都可以查看FITS图像的头文件,但在实践中发现,对于存在“千年虫”问题的FITS图像,即头文件的键值对存在形如“DATE-OBS=MM/DD/YYY”的格式,SAOImage DS9可能出现头文件信息的键值对数量显示不完整的问题。此外,目前Astrometrica只能手动修改观测时间的头文件信息,而MaxIm DL可以编辑大部分的头文件信息,包括增加与删除键值对。
Astrometrica和MaxIm DL均能对图像进行灰度变换的调整,使图像有更好的视觉效果。在图像变换功能上,MaxIm DL的功能要比Astrometrica强大得多。MaxIm DL除了能调整简单的像素灰度变换外,还支持热像素的忽略、大量滤波器的使用、图像任意角度的旋转、反卷积、增加噪声、像素合并、剔除坏像素等功能。当拍摄的CCD图像角度与星图不匹配时,旋转图像的角度可以帮助我们手动匹配星像。在天体测量图像的处理过程中,不建议对图像做除平场校正外的其他图像变换,如使用滤波器、反卷积操作,只能使图像有更好的视觉效果,对位置测量结果不会有明显的提高。Astrometrica在用户手册术语表的校正说明中也提到:“进一步的图像处理(如直方图缩放、使用滤波器或反卷积)可能会扭曲星像的质心与光通量。”
1.2 平场校正CCD图像的平场校正是测光重要的一步,有时也把该技术应用在天体测量中。Astrometrica和MaxIm DL均有平场校正功能,Astrometrica只能使用1幅暗场图像(Dark)和1幅平场(Flat)图像进行校正,而MaxIm DL则支持多幅暗场、平场和本底(Bias)图像校正。此外,MaxIm DL可以把不同类型的校正图像分组,每组通过均值、中值等方法生成一张“主”(Master)图像,以节省校正图像的内存空间,提高校正的运算速度。MaxIm DL还可以自定义调整图像的“底座”(Pedestal)像素值,以确保图像的像素值为正数。当平场处理后的图像需要作为其他工具的输入图像时,一般结合使用MaxIm DL中批量保存与转换功能,这样能快速地批量输出平场校正后的图像。
1.3 Astrometrica参数的设置与归算方法在CCD的参数设置中,有时望远镜焦距和像素大小的设置可能难以确定,因为这些信息不一定包含在图像的头文件中,本文给出两种确定上述两个参数的方法。实际上,像素大小与望远镜焦距之比就是图像的比例尺,可以这样认为,只要两者之间的比例是正确的,Astrometrica也能正确地进行数据归算和图像堆叠。第1种确定图像比例尺的方法是把图像上传至astrometry.net获得,详细的算法可以参考文[9];第2种确定比例尺的方法是把图像中两颗恒星与星图匹配,通过坐标转换关系计算比例尺。
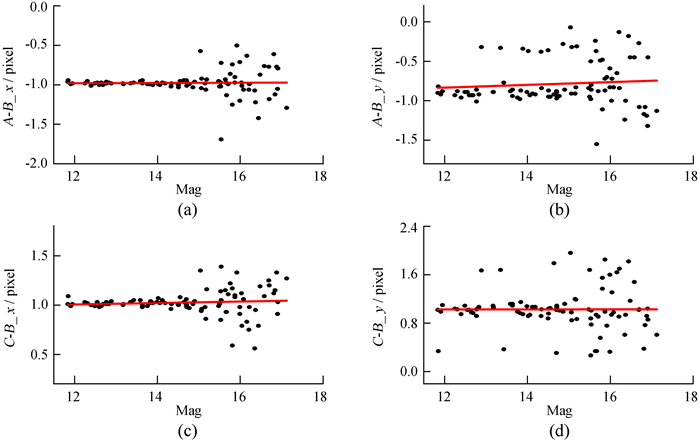
使用Astrometrica得出数据归算的结果对于高精度的天体测量来说是不够的。在软件的设置中,参考星的搜索半径(Search Radius)、星表极限星等(Upper/Lower Limit)、检测目标的孔径(Aperture Radius)、检测极限(Detection Limit)等参数的调整都影响参考星的精度。参考星的搜索半径是指图像中搜索的恒星与星表中参考星位置的最大误差,若搜索的恒星与星表中参考星的位置偏差小于设置的参数,系统认为这两颗星是同一颗。星表的极限星等设置影响星表中用于匹配的参考星,所以把该参数调整到星像未饱和的亮星区间范围。检测目标的孔径和检测极限按照用户手册推荐的参考数值范围进行设置对于参考星精度的影响不大。实验发现,参考星搜索半径参数的调整对参考星精度的影响较大,本文利用1 m光学望远镜连续拍摄的M35星团的3幅原始的(未做平场校正等处理)CCD图像进行实验对比,把3幅图像分别命名为A,B和C,以B为基准,对相同参考星的二维坐标的残差(即A,C中每颗参考星的坐标与B中相同参考星的坐标之差)进行统计。图 1、图 2分别显示了参考星搜索半径为1像素和0.51像素图像坐标的残差情况。
|
| 图 1 参考星搜索半径设置为1像素时A和C两幅图的参考星在二维坐标的残差分布 Fig. 1 Residual distribution of reference stars in two-dimensional coordinates of A and C images when the search radius of reference stars is set to 1 pixel |
|
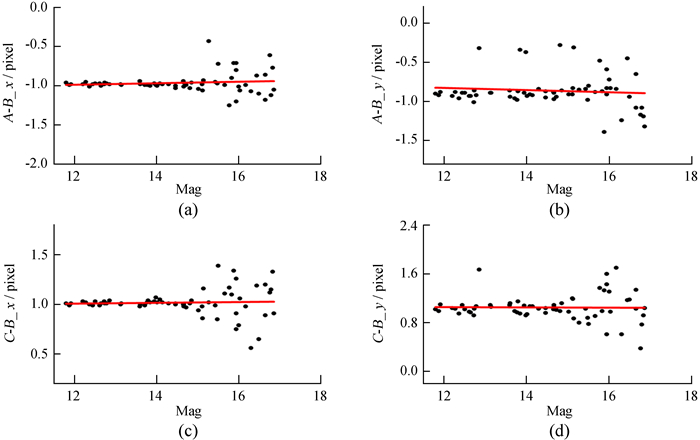
| 图 2 参考星搜索半径设置为0.51像素时A和C两幅图的参考星在二维坐标的残差分布 Fig. 2 Residual distribution of reference stars in two-dimensional coordinates of A and C images when the search radius of reference stars is set to 0.51 pixel |
从图 1可以看到,在图像y方向的残差存在异常点,有若干参考星在位置上偏离正常值约0.7像素。在图 2中,把参考星的搜索半径设置为0.51像素时(0.51像素是该软件能设置的最小值),可以看到大部分异常点消失,参考星的精度提高。参考星的搜索半径应设置得尽可能小,以提高参考星的测量精度。当然,也可以调整测量的极限残差(Astrometric Limit)来选择高精度的参考星进行匹配,但是很难确定并设置测量极限残差的最优值,它与底片常数阶数的选择、参考星匹配的数量和观测资料等有较大的关系。如图 1(d)的残差异常点,Astrometrica对于同一颗参考星似乎搜索了2次或3次,且每次恒星中心的坐标不同。Astrometrica在数据归算过程中同一颗星被搜索成2颗或3颗星的现象如图 3。

|
| 图 3 (a),(b)分别是Astrometrica把同一颗恒星搜索成2颗、3颗不同的恒星 Fig. 3 The (a) and (b) respectively show that Astrometrica searches a star into two and three different stars |
对于暗弱或圆度较大的星像,Astrometrica可能会把同一颗星搜索成2颗或3颗不同的恒星,也就是说,Astrometrica对于搜星过于敏感。为了尽可能消除这种搜星的敏感性对参考星精度的影响,建议参考星的搜索半径设置到最小,即0.51像素。
1.4 CCD图像堆叠CCD图像堆叠可以提高图像的信噪比,对暗星测光和位置测量有较大的帮助。Astrometrica和MaxIm DL都有图像堆叠功能。在Astrometrica中,设置参数和数据归算都是图像堆叠的前置条件。在堆叠的参数设置中,目标移动的速度与角度的调整一般用于巡天工作。当用于恒星位置测量时,上述两个参数应设置为0。Astrometrica有数值叠加(Sum)、均值叠加(Average)、中值叠加(Median)3种堆叠方法。通常,数值叠加方法适用于巡天而不适用于位置测量,因为数值叠加方法会导致大部分的星像饱和,从而影响星像质量。均值与中值均适用于位置测量,关于两者的细节,在第2部分进行详细的对比实验与讨论。通过观察Astrometrica的运行和查看日志文件不难看出它在图像堆叠中的运作机制:首先,Astrometrica在进行图像堆叠前对两幅图像进行数据归算;然后,根据数据归算的结果把需要堆叠的图像对齐(图像x轴与y轴),Astrometrica在图像对齐时只考虑图像两个坐标方向的简单平移;最后,Astrometrica根据设置的参数与叠加方法进行图像堆叠。
在MaxIm DL的堆叠过程中,有图像分类、选择符合质量的图像、图像对齐、调整颜色、选择叠加方法5个步骤。在图像分类过程中,MaxIm DL可以根据所选的文件夹以及观测的目标和观测时使用的滤光片进行分类,此外,在叠加工作前进行平场校正、合并像素等操作。在选择符合质量的图像过程中,MaxIm DL把每幅图像的星像半高全宽(FWHM)、圆度(Roundness)、光强(Itensity)和对比度(Contrast)作为质量评估的标准。相比Astrometrica,在图像对齐的过程中,MaxIm DL的星像自动对齐模式多考虑了图像的旋转与图像的缩放关系,这相当于考虑了4参数模型(转换过程中用到了4个参数)。在图像的叠加方法选择时,MaxIm DL除了可选数值叠加、均值叠加、中值叠加方法外,还提供了标准差(Sigma Clip)、迭代的标准差(SD Mask)、抖动(Drizzle)3种方法的叠加,关于这些叠加方法的详细说明可参考MaxIm DL用户手册。
2 Astrometrica与MaxIm DL图像堆叠方法的比较实验实验中没有考虑数值叠加方法与抖动方法,因为对图像进行数值叠加会造成大量星像饱和,而抖动叠加方法主要用于欠采样、抖动观测的图像。我们比较了Astrometrica提供的均值叠加、中值叠加算法和MaxIm DL提供的均值叠加、中值叠加、标准差叠加、迭代的标准差叠加算法。均值叠加算法将一组图像对齐后,取每幅图像各位置像素的平均值,而中值叠加算法则取每幅图像各位置像素的中值。标准差剔除算法将每幅图像各位置像素进行标准差剔除后再取剩余像素的平均值,而迭代的标准差算法是一种多次迭代的标准差(软件的推荐值为0.5倍标准差,迭代3次)算法。
本文选取1 m光学望远镜拍摄的M35星团的CCD图像进行实验,包括2020年2月7日与2020年3月5日拍摄的两组共50幅使用I滤光片观测的CCD图像,每幅图像的曝光时间为60 s。这两组观测资料的大气视宁度较好,图像抖动程度较小,大部分图像中星像的半高全宽为4.5~6像素。但观测时接近月望,所以图像的天空背景相对较高。
在处理过程中,(1)使用MaxIm DL对观测的若干平场和本底图像进行平场校正;(2)使用MaxIm DL对平场校正后的图像进行质量筛选,其中,2020年2月7日的筛选标准为半高全宽不大于5像素,圆度不大于0.2,2020年3月5日的筛选标准为半高全宽不大于6像素,圆度不大于0.2;(3)在每组观测图像中选择15幅满足质量要求的图像,每5幅为一组,分别使用Astrometrica和MaxIm DL选择不同的方法进行图像叠加,在MaxIm DL的叠加操作中,其他的参数与设置均使用系统默认值或推荐值且保持不变;(4)对两组共18幅实验图像(每5幅图像叠加后的图像为1幅实验图像)进行数据归算,参照Gaia DR2星表[10]的位置,具体可参考文[11]的数据归算方法。图 4~图 9给出了2月7日观测资料中每种叠加方法恒星随星等的精度分布情况,3月5日观测资料在位置测量中精度分布情况与2月7日相似。
|
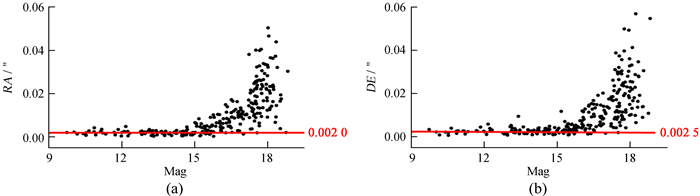
| 图 4 Astrometrica均值叠加后恒星观测值-计算值(O-C)的标准差在赤经、赤纬的分布情况,其中红色实线表示亮于14等星标准差的中位数(下同) Fig. 4 The distribution of stars′ standard deviation of observed minus computed (O-C) in right ascension and declination after Astrometrica′s average stacking, where the red solid line represents the median of the standard deviation brighter than 14 magnitude (same hereinafter) |
|
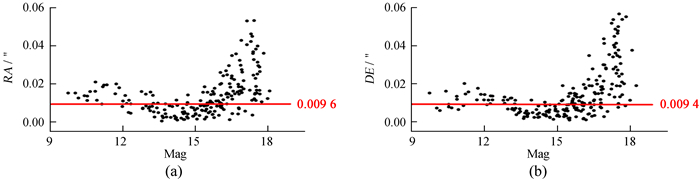
| 图 5 Astrometrica中值叠加后恒星观测值-计算值(O-C)的标准差在赤经、赤纬的分布情况 Fig. 5 The distribution of stars′ standard deviation of observed minus computed (O-C) in right ascension and declination after Astrometrica′s median stacking |
|
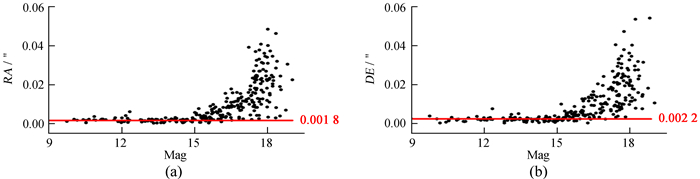
| 图 6 MaxIm DL均值叠加后恒星观测值-计算值(O-C)的标准差在赤经、赤纬的分布情况 Fig. 6 The distribution of stars′ standard deviation of observed minus computed (O-C) in right ascension and declination after MaxIm DL′s average stacking |
|
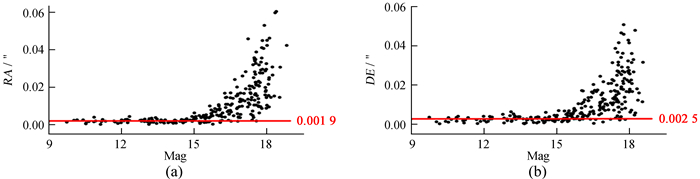
| 图 7 MaxIm DL中值叠加后恒星观测值-计算值(O-C)的标准差在赤经、赤纬的分布情况 Fig. 7 The distribution of stars′ standard deviation of observed minus computed (O-C) in right ascension and declination after MaxIm DL′s median stacking |
|
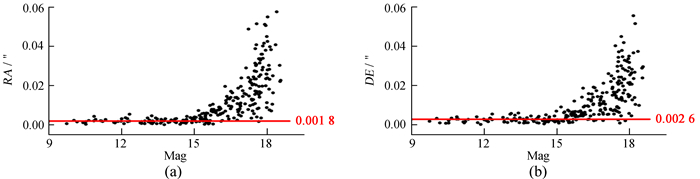
| 图 8 MaxIm DL标准差叠加后恒星观测值-计算值(O-C)的标准差在赤经、赤纬的分布情况 Fig. 8 The distribution of stars′ standard deviation of observed minus computed (O-C) in right ascension and declination after MaxIm DL′s sigma clip stacking |
|
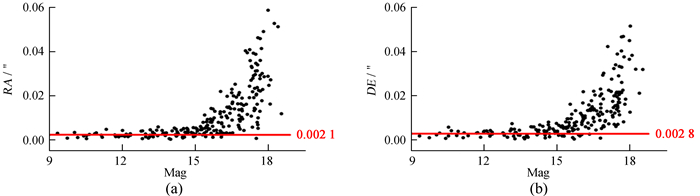
| 图 9 MaxIm DL迭代的标准差叠加后恒星观测值-计算值(O-C)的标准差在赤经、赤纬的分布情况 Fig. 9 The distribution of stars′ standard deviation of observed minus computed (O-C) in right ascension and declination after MaxIm DL′s SD Mask stacking |
从图 4~图 9可以看出,赤纬方向位置精度的弥散程度比赤经方向略大。此外,使用Astrometrica中值叠加方法处理的图像(见图 5)在赤经、赤纬方向的精度分布情况异常,即星等亮于14等的恒星在赤经、赤纬方向的精度比亮度在14等左右的恒星的精度还要差。分析认为,导致这种异常现象的原因是Astrometrica在进行图像对齐时使用的超定方程组的数据均来自于14等星左右的坐标。
3 Astrometrica与MaxIm DL的配合使用Astrometrica和MaxIm DL的CCD图像处理功能对天体测量的研究都有较大的帮助,且它们考虑的功能和细节略有不同。文[5]在位置测量的处理中,背景调整、平场校正、数据归算等步骤都基于Astrometrica进行。实践中可以结合两个软件的优势进行CCD图像处理,Astrometrica在平场校正时只能使用一幅平场图像和一幅暗场图像,而MaxIm DL可以使用多幅图像。先使用MaxIm DL进行CCD图像的平场校正,再使用Astrometrica对校正后的图像进行数据归算。文[6]使用Astrometrica通过数值和中值叠加CCD图像的方式巡天,发现了280颗近地小行星。从图 5可以看出,使用Astrometrica对CCD图像进行中值叠加后存在位置测量精度异常的情况。MaxIm DL在图像的堆叠中也考虑了更多的参数与细节问题,此外,MaxIm DL在图像的中值叠加时不会出现位置测量精度异常的情况。实践中可以先使用MaxIm DL进行CCD图像的质量筛选和图像堆叠,再使用Astrometrica进行巡天。综上所述,结合Astrometrica和MaxIm DL两个软件对天体测量和巡天工作可能有较大的改进。
4 总结与展望本文介绍了Astrometrica和MaxIm DL两个软件在天体测量中的应用,对两个软件从CCD图像的读写与变换、平场校正、参数的设置与归算方法、图像堆叠进行了详细的比较和研究。本文使用1 m光学望远镜拍摄的两组M35星团的观测资料比较和探究了Astrometrica和MaxIm DL两个软件图像堆叠功能对恒星位置测量精度的影响。研究发现,使用Astrometrica中值叠加后的图像在位置测量的精度上出现异常,结合两个软件的特点,提出了两个软件配合使用的方法。后续的研究工作中,进一步探究MaxIm DL的一些图像处理功能,并应用在天体测量工作中,以提高位置测量的准确度和精度。
致谢: 感谢云南天文台1 m光学望远镜运行团组在新冠肺炎疫情期间提供的观测服务。
| [1] | RAAB H. Astrometrica software[CP/OL]. [2020-05-27]. http://www.astrometrica.at. |
| [2] | Diffraction Limited. MaxIm DL software[CP/OL]. [2020-05-27]. https://diffractionlimited.com/product/maxim-dl. |
| [3] |
孙浩民, 邓辉, 梅盈, 等. 基于Python-casacore的射电测量集文件生成方法[J]. 天文研究与技术, 2020, 17(2): 210–216 SUN H M, DENG H, MEI Y, et al. Measurement Set file generating method based on Python-casacore[J]. Astronomical Research & Technology, 2020, 17(2): 210–216. |
| [4] |
张珊瑚, 邱丹, 聂嘉潞, 等. 基于MATLAB的一维光谱可视化与分析工具的设计与实现[J]. 天文研究与技术, 2020, 17(1): 121–128 ZHANG S H, QIU D, NIE J L, et al. Design and implementation of visualization and analysis tool for 1-D spectrum based on MATLAB[J]. Astronomical Research & Technology, 2020, 17(1): 121–128. |
| [5] | QIAO R C, XI X J, DOURNEAU G, et al. CCD astrometric observations of Phoebe in 2005-2008[J]. Monthly Notices of the Royal Astronomical Society, 2011, 413(2): 1079–1082. DOI: 10.1111/j.1365-2966.2011.18214.x |
| [6] | VADUVESCU O, HUDIN L, MOCNIK T, et al. 280 one-opposition near-Earth asteroids recovered by the EURONEAR with the Isaac Newton Telescope[J]. Astronomy & Astrophysics, 2011, 609: A105. |
| [7] | GUPTA A C, GAUR H, WⅡTA P J, et al. Characterizing optical variability of OJ 287 in 2016-2017[J]. The Astronomical Journal, 2019, 157(3): 95. DOI: 10.3847/1538-3881/aafe7d |
| [8] | JOYE W A, MANDEL E. New features of SAOImage DS9[C]//Astronomical Data Analysis Software and Systems Ⅻ ASP Conference Series. 2003: 489-492. |
| [9] | LANG D, HOGG D W, MIERLE K, et al. Astrometry.net: blind astrometric calibration of arbitrary astronomical images[J]. The Astronomical Journal, 2010, 139(5): 1782–1800. DOI: 10.1088/0004-6256/139/5/1782 |
| [10] | Gaia Collaboration, BROWN A G A, VALLENARI A, et al. Gaia data release 2. summary of the contents and survey properties[J]. Astronomy & Astrophysics, 2018, 616: A1. |
| [11] | LIN F R, PENG J H, ZHENG Z J, et al. Characterization of the precision premium in astrometry[J]. Monthly Notices of the Royal Astronomical Society, 2019, 490(3): 4382–4387. DOI: 10.1093/mnras/stz2871 |


