2. 广西相对论天体物理重点实验室, 广西 南宁 530004
2. Guangxi Key Laboratory for the Relativistic Astrophysics, Nanning 530004, China
耀变体(Blazar)是活动星系核(Active Galactic Nuclei, AGN)中比较特殊的一个子类,是最活跃的天体之一,其辐射主要来自喷流中的高能粒子,由于相对论聚束效应,在伽玛波段可以观测到辐射活动。耀变体可分为平谱射电耀变体(FSRQ)和蝎虎座BL型天体(BL Lac)两个子类[1],观测特征包括高光度、高偏振、快速光变以及非热辐射等[2];能谱分布(Spectra Energy Distribution, SED)呈现双峰结构,低能峰是由于同步辐射产生,高能峰是由于电子的逆康普顿辐射过程或者强子辐射产生[3-4]。多普勒因子的估算方法有很多种,其中,通过射电光变估算多普勒因子是比较简单的一种,因而被广泛应用[5-6]。光变研究能探索耀变体内部的辐射过程和物理机制,因此,研究天体的光变及其可能的周期性,对了解活动星系核具有重要意义。
耀变体CGRaBS J0835 + 6835(BWE 0830 + 6845)是一颗红移z=1.414的天体(α=08 35 47.608 086 678 5,δ=+68 35 11.493 386 746)[7]。文[8]测得这个源在R波段的流量为0.000 13 mJy,文[9]在研究GHz峰频的样本源时,给出了此源在325 MHz,609 MHz和5 GHz等不同频率下的流量密度。本文利用欧文斯谷射电天文台的长时间监测数据(15 GHz)研究CGRaBS J0835 + 6835的射电光变,检验是否存在准周期振荡,还使用双指数函数拟合爆发过程,检验是否存在明显的聚束效应。目前,分析耀变体光变曲线准周期振荡的方法主要有两种:LSP方法[10]和加权小波Z变换[11],这两种方法非常适合处理非等间隔数据。本文利用这两种方法对耀变体CGRaBS J0835 + 6835的15 GHz射电波段的光变周期进行研究,并对结果的可靠性和置信度进行评估。
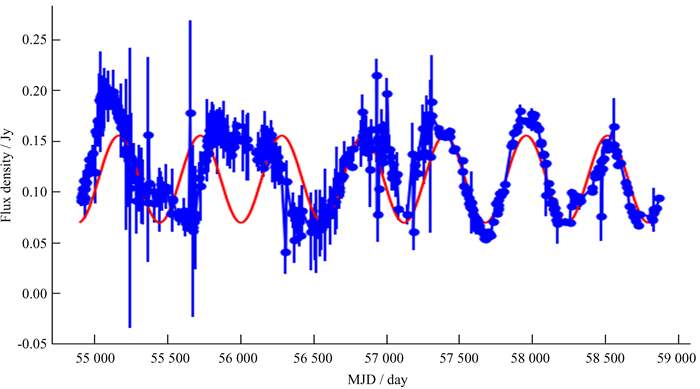
1 光变曲线如图 1是来自欧文斯谷射电天文台40 m望远镜观测的耀变体CGRaBS J0835 + 6835在15 GHz射电波段的光变曲线,去除少量的坏点后,采用460个数据点,约化儒略日MJD范围约为54 908~58 871。采用光变指数A[12-13]判断天体的活跃程度:
| $ A = \frac{{{f_{\max }} - {f_{\min }}}}{{{f_{\max }} + {f_{\min }}}}. $ | (1) |
|
| 图 1 蓝线表示耀变体CGRaBS J0835 + 6835在15 GHz射电波段的光变曲线,红线表示正弦函数对光变曲线的大致拟合 Fig. 1 The blue line represents the light curve of the blazar CGRaBS J0835 + 6835 in the 15 GHz radio band, and the red line represents the rough fit of the sine function to the light curve |
其中,fmax和fmin分别为流量的最大值和最小值,光变指数A值越大表示天体越活跃。通过计算可以得到CGRaBS J0835 + 6835在射电波段的光变指数为0.98,这表明CGRaBS J0835 + 6835是个非常活跃的天体。
2 光变曲线的周期分析 2.1 LSP方法检测隐藏在噪声中的周期信号是天文数据时间序列分析的一个重要目标。LSP方法可以对非均匀采样的时间序列周期图进行相位修正,能够在一定范围内对非均匀采样的时间间隔引起的误报周期进行修正[10]。因此,LSP方法能很好地寻找隐藏在噪声中的准周期振荡光变。LSP方法的原理是基于傅里叶变换,使用正弦函数模型,基本公式为[14-15]
| $ Px(\omega ) = \frac{1}{2}\left\{ {\frac{{\sum\limits_{j = 1}^{{N_0}} {\left[ {x\left( {{t_j}} \right) - \bar x} \right]} \cos \omega \left( {{t_j} - \tau } \right)}}{{\sum\limits_{j = 1}^{{N_0}} {{{\cos }^2}} \omega \left( {{t_j} - \tau } \right)}} + \frac{{\sum\limits_{j = 1}^{{N_0}} {\left[ {x\left( {{t_j}} \right) - \bar x} \right]} \sin \omega \left( {{t_j} - \tau } \right)}}{{\sum\limits_{j = 1}^{{N_0}} {{{\sin }^2}} \omega \left( {{t_j} - \tau } \right)}}} \right\}, $ | (2) |
其中,τ为对应时间t的相位修正,计算公式为
| $ \tan (2\omega \tau ) = \frac{{\sum\limits_{j = 1}^{{N_0}} {{{\sin }^2}} 2\omega {t_j}}}{{\sum\limits_{j = 1}^{{N_0}} {{{\cos }^2}} 2\omega {t_j}}}. $ | (3) |
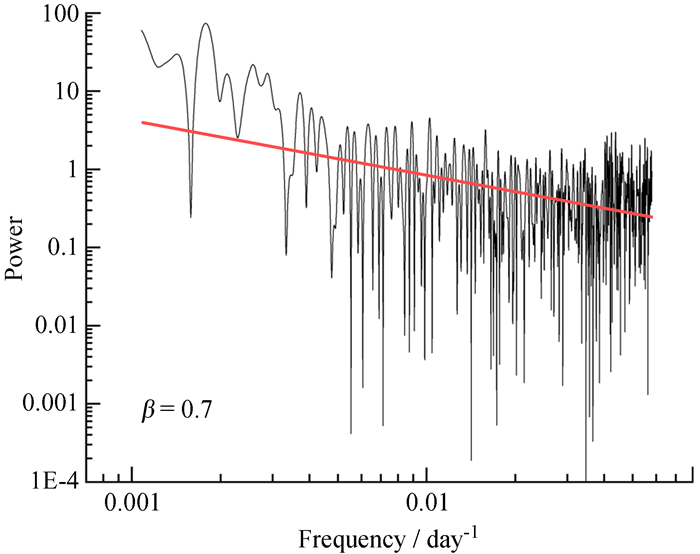
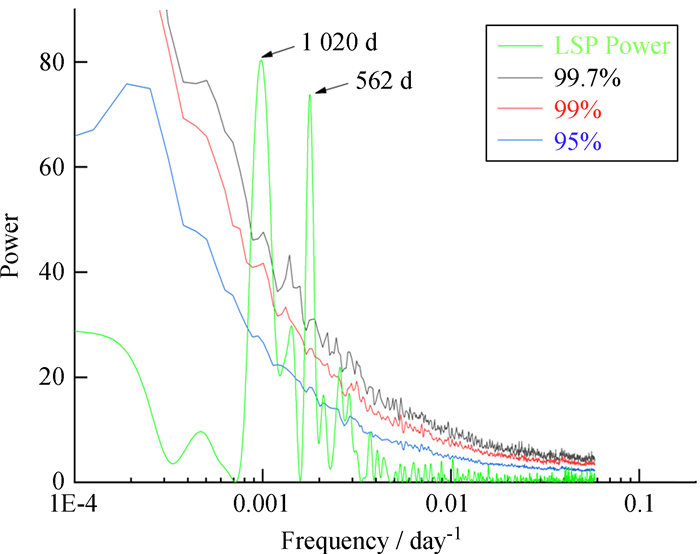
LSP方法有几个优点是离散傅里叶变换所不具备的:首先,公式中包含时间项t,使得周期计算不随时间原点的变化而变化;其次,这种形式使得周期图分析完全等价于正弦曲线对数据的最小二乘拟合。为了验证LSP方法计算准周期的正确性,如图 2,先对周期图进行幂率拟合,得到蒙特卡罗方法计算置信度所需参数的幂率指数β[16],然后用Python编写程序计算CGRaBS J0835 + 6835的置信度,结果如图 3。图 3中绿色线表示准周期图,峰值就是准周期结果;蓝色、红色、黑色线分别表示蒙特卡罗模拟的95%、99%、99.7%置信度。图 3中的绿线有两个明显的峰值分别为562天和1 020天,并且两个峰的置信度都超过99.7%,说明两个峰值结果都是可靠的,但是1 020天约为562天的两倍,所以取最小正周期即562天作为CGRaBS J0835 + 6835的准周期结果。
|
| 图 2 CGRaBS J0835 + 6835在射电波段的对数幂率谱 Fig. 2 CGRaBS J0835 + 6835 object logpower spectrum in radio band |
|
| 图 3 CGRaBS J0835 + 6835在射电波段准周期震荡置信度的蒙特卡罗模拟分析结果 Fig. 3 The Monte Carlo simulation analysis results of the confidence level of the QPO of CGRaBS J0835 + 6835 in radio band |
小波分析(Wavelet Aanlysis)是一种新的分析方法,是继傅里叶分析之后纯粹数学和应用数学完美结合的又一典范。利用Morlet小波作为小波母函数进行变换,复Morlet小波为[17]
| $ \psi (t) = {{\rm{e}}^{ - {t^{2/2}}}}\left( {{{\rm{e}}^{{\rm{i}}{w_0}t}} - {{\rm{e}}^{ - {w_0}/2}}} \right), $ | (4) |
文[18]定义了加权小波变换
| $ WWT = \frac{{\left( {{N_{{\rm{eff }}}} - 1} \right){V_y}}}{{2{V_x}}}, $ | (5) |
其中,
| $ {N_{{\rm{eff }}}} = \frac{{{{\left( {\sum {{\omega _\alpha }} } \right)}^2}}}{{\sum {\omega _\alpha ^2} }};{V_x} = \frac{{\sum\limits_\alpha {{\omega _\alpha }} {x^2}\left( {{t_\alpha }} \right)}}{{\sum\limits_\beta {{\omega _\beta }} }} - {\left[ {\frac{{\sum\limits_\alpha {{\omega _\alpha }} x\left( {{t_\alpha }} \right)}}{{\sum\limits_\beta {{\omega _\beta }} }}} \right]^2};{V_y} = \frac{{\sum\limits_\alpha {{\omega _\alpha }} {y^2}\left( {{t_\alpha }} \right)}}{{\sum\limits_\beta {{\omega _\beta }} }} - {\left[ {\frac{{\sum\limits_\alpha {{\omega _\alpha }} y\left( {{t_\alpha }} \right)}}{{\sum\limits_\beta {{\omega _\beta }} }}} \right]^2}. $ |
由于小波形状的变化,低频部分的有效数据Neff 比高频部分的有效数据多,因此,加权小波变换的值向高频部分偏移,导致结果出现偏差,于是文[18]根据Z统计量定义了加权小波Z变换为[10]
| $ Z = \frac{{\left( {{N_{{\rm{eff}}}} - 3} \right){V_y}}}{{2\left( {{V_x} - {V_y}} \right)}}. $ | (6) |
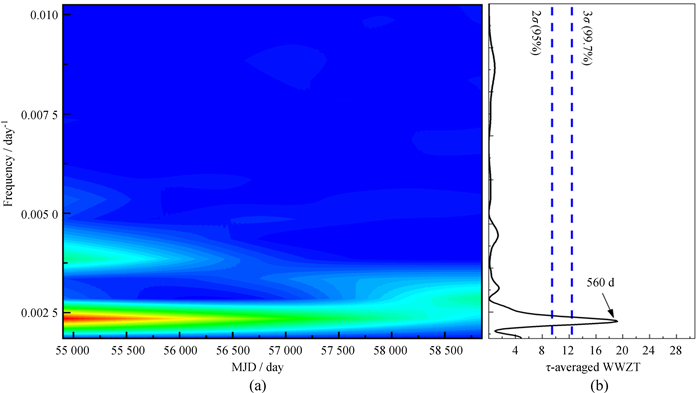
利用(6)式可以得到如图 4的准周期图,(a)是时间周期平面中加权小波Z变换功率彩色缩放的分布,(b)是时间平均功率(黑色曲线)作为周期的函数图,其中蓝色虚线表示置信度在99.7%和95%的位置。根据加权小波Z变换图的极大值可以确定光变曲线的周期。图 4显示了一个明显的极大值560天且置信度超过99.7%,也就是说560天的准周期结果是可靠的。
|
| 图 4 加权小波Z变换方法对CGRaBS J0835 + 6835在射电波段准周期振荡的分析结果 Fig. 4 The WWZT test result for QPO search CGRaBS J0835 + 6835 at radio band |
多普勒因子可以通过喷流中物质流速度V以及视角θ两个本征参数定义,然而这两个量都是难以直接观测的,因此,用间接方法估算多普勒因子。在各种估算多普勒因子的方法中,通过射电光变估算相对比较简单,因而被广泛应用。
文[19-20]详细介绍了亮温度和双指数函数公式及估算多普勒因子的过程。双指数函数公式为
| $ F(t) = {F_{\rm{c}}} + {F_0}{\left( {{{\rm{e}}^{\frac{{{t_0} - t}}{{{t_{\rm{r}}}}}}} + {{\rm{e}}^{\frac{{t - {t_0}}}{{{t_{\rm{d}}}}}}}} \right)^{ - 1}}. $ | (7) |
利用亮温度公式估算CGRaBS J0835 + 6835的射电亮温度分布在3.7 × 1013~2.3 × 1014 K,超过逆康普顿极限温度或平衡亮温度几个量级, 表明此源的射电辐射存在明显的聚束效应。双指数函数拟合的6个爆发过程如图 5。类似文[21]选取平衡亮温度作为内禀亮温度,本文进一步估算对应的光变多普勒因子。每个爆发过程的拟合参数如表 1,第1列为约化儒略日范围;第2列为拟合所得的约化最小残差平方和
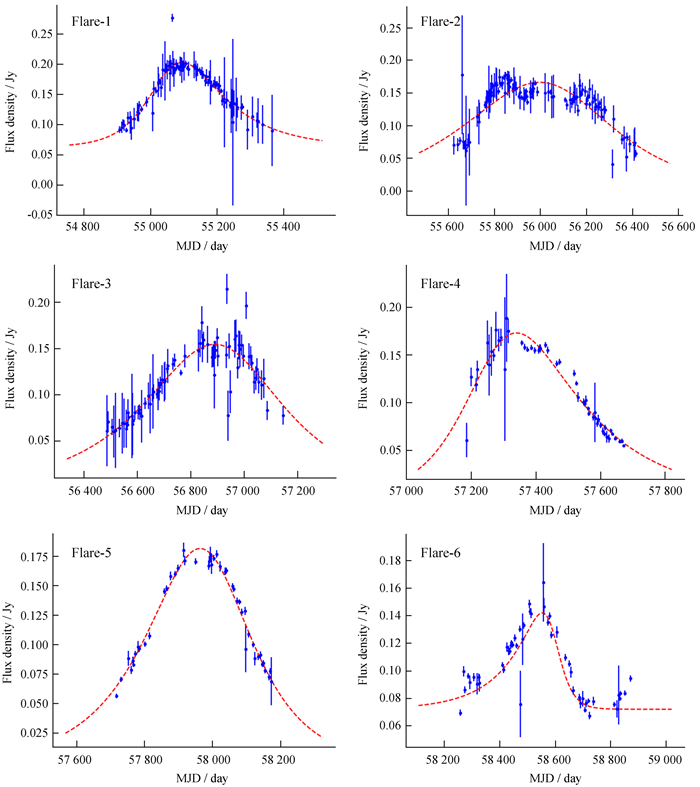
|
| 图 5 双指数函数对CGRaBS J0835 + 6835的6个爆发过程的曲线拟合。MJD为约化儒略日,单位是天 Fig. 5 The double exponential function fits the curves of the 6 flares of CGRaBS J0835 + 6835. MJD is Modified Julian Day, the unit is day |
| Peak range | χ2/dof | to | Fc | |
| 54 908.9-55 366.2 | 1.52E-04 | 1.54 | 55 062.97 ± 26.79 | 0.06 ± 0.04 |
| 55 623.2-56 414.8 | 3.98E-04 | 2.94 | 55 978.50 ± 9.63 | 0.07 ± 0.04 |
| 56 487.6-57 146.8 | 3.14E-04 | 1.63 | 56 909.21 ± 27.48 | 0.14 ± 0.02 |
| 57 186.7-57 671.5 | 1.43E-04 | 1.95 | 57 336.36 ± 26.94 | 0.24 ± 0.06 |
| 57 717.3-58 174.0 | 4.23E-04 | 1.15 | 57 978.93 ± 11.71 | 0.11 ± 0.01 |
| 58 257.7-58 724.5 | 1.08E-04 | 2.79 | 58 589.75 ± 18.08 | 0.07 ± 0.04 |
| F0 | tr | td | δv | |
| 0.26 ± 0.03 | 140.51 ± 49.16 | 69.25 ± 24.09 | 9.63 ± 0.34 | |
| 0.33 ± 0.11 | 152.17 ± 48.32 | 98.21 ± 56.41 | 8.87 ± 0.68 | |
| 0.31 ± 0.17 | 146.58 ± 20.94 | 64.17 ± 44.78 | 10.43 ± 0.35 | |
| 0.33 ± 0.03 | 95.97 ± 28.51 | 123.84 ± 24.31 | 9.36 ± 0.12 | |
| 0.36 ± 0.03 | 123.38 ± 43.37 | 53.92 ± 19.23 | 11.77 ± 0.84 | |
| 0.11 ± 0.01 | 33.51 ± 38.41 | 128.52 ± 47.14 | 14.45 ± 0.23 | |
本文通过收集欧文斯谷射电天文台的长时间监测数据,利用LSP方法和加权小波Z变换方法对CGRaBS J0835 + 6835的射电波段光变曲线的准周期振荡进行分析。LSP方法分析得到的准周期约为562天和1 020天,并且置信度都大于3σ(99.7%),1 020天大约是562天的两倍,故可以认为CGRaBS J0835 + 6835的准周期约为562天。加权小波Z变换方法得到的准周期约为560天,置信度也超过了3σ(99.7%)。两种检测准周期的方法得到的结果都大致约为560天,检验的结果相互印证,所以,我们认为CGRaBS J0835 + 6835的准周期约为560天。同时,本文利用双指数函数拟合了6个爆发过程,得到δV的值分布在8.87 ± 0.68~14.45 ± 0.23,平均值约为10.76。结果表明,CGRaBS J0835 + 6835的射电辐射存在明显的聚束效应,支持相对论性喷流模型。目前,耀变体长周期光变的物理模型仍然是悬而未决的问题,为了解决这些问题,天文学家提出了很多物理模型,例如双黑洞模型[23]、螺旋喷流模型[24]和薄吸积盘理论[25]等。
根据CGRaBS J0835 + 6835 560天的准周期,其物理过程可能是喷流的螺旋运动[26]。文[27]在给出的观测准周期P与实际物理驱动周期Pd之间的关系公式为
| $ {P_{\rm{d}}} \approx \frac{{\gamma _{\rm{b}}^2}}{{1 + z}}P, $ | (8) |
其中,红移z=1.414[7];γb为体洛伦兹因子,约等于7.5[28]。基于(8)式可以得到实际物理驱动周期Pd≈35.75年,另外,如果γb=15作为参数[29],Pd≈143.00年。当主黑洞和次黑洞的质量比R ≤ 1/3,称为主并合;如果3 ≤ R ≤ 104,称为次并合[30]。无论质量比如何,主黑洞的质量都可以用公式[31]
| $ M \approx P_{\rm{d}}^{\frac{8}{5}}{R^{\frac{3}{5}}}{10^6}{M_ \odot } $ | (9) |
估计,其中,Pd以年为单位,对于超大质量双黑洞系统的主并合,质量比可以假设为R=3/2,代入(9)式,得到CGRaBS J0835 + 6835主黑洞质量大约为M=3.7 × 108M⊙。同理,如果使用γb=15作为参数,次并合的超大质量双黑洞系统的主黑洞质量为M=3.5 × 109M⊙,故CGRaBS J0835 + 6835的主黑洞质量约为3.7 × 108M⊙~3.5 × 109M⊙。
| [1] | URRY C, PADOVANI P. Unified schemes for radio-loud Active Galactic Nuclei[J]. Publications of the Astronomical Society of the Pacific, 1995, 107(715): 803–845. DOI: 10.1086/133630 |
| [2] | DONDI L, GHISELLINI G. Gamma-ray-loud blazars and beaming[J]. Monthly Notices of the Royal Astronomical Society, 1995, 273(3): 583–595. DOI: 10.1093/mnras/273.3.583 |
| [3] | XIE G Z, BAI J M, ZHANG X, et al. The massive black hole in the center of the active galaxy MRK 421[J]. Astronomy & Astrophysics, 1998, 334: L29–L31. |
| [4] | ZHANG X, ZHAO G, ZHENG Y G, et al. CCD photometry and optical variability of gamma-ray-loud BL Lacertae object OJ 287 in a low, fainter state[J]. The Astronomical Journal, 2007, 133(5): 1995–2000. DOI: 10.1086/512126 |
| [5] | VALTAOJA E, LAHTEENMAKI A, TERASRANTA H, et al. Total flux density variations in extragalactic radio sources. Ⅰ. decomposition of variations into exponential flares[J]. The Astrophysical Journal Supplement, 1999, 120(1): 95–99. DOI: 10.1086/313170 |
| [6] | LÄHTEENMÄKI A, VALTAOJA E. Total flux density variations in extragalactic radio sources. Ⅲ. Doppler boosting factors, Lorentz factors and viewing angles for Active Galactic Nuclei[J]. The Astrophysical Journal, 2009, 521(2): 493–501. |
| [7] | MASSARO E, GIOMMI P, PAOLO M, et al. Roma-BZCAT: a multifrequency catalogue of blazars[J]. Astronomy & Astrophysics, 2009, 495(2): 691–697. |
| [8] | HEALEY S E, ROMANI R W, COTTER G, et al. CGRaBS: an all-sky survey of Gamma-Ray Blazar Candidates[J]. The Astrophysical Journal Supplement Series, 2008, 175(1): 97–104. DOI: 10.1086/523302 |
| [9] | SNELLEN I A G, SCHILIZZI R T, BRUYN A G D, et al. A new sample of faint Gigahertz Peaked Spectrum radio sources[J]. Astronomy & Astrophysics, 1998, 13(1): 18–33. |
| [10] | REJKUBA M, MINNITI D, SILVA D R. Long period variables in NGC 5128-I catalogue[J]. Astronomy & Astrophysics, 2003, 406(1): 75–85. |
| [11] | FOSTER G. Time series analysis by projection I statistical properties of Fourier analysis[J]. The Astrophysical Journal, 1996, 111(1): 541–554. |
| [12] | ZHANG L, FAN J H, CHENG K S. The multiwavelength Doppler factors for a sample of Gamma-ray loud blazars[J]. Publications of the Astronomical Society of Japan, 2002, 54(2): 159–169. DOI: 10.1093/pasj/54.2.159 |
| [13] | LI H Z, CHEN L E, DAI H, et al. The periodicity analysis of the light curve of 3C 279 and implications for the precession jet[J]. Publications of the Astronomical Society of the Pacific, 2009, 121(885): 1172–1179. DOI: 10.1086/648433 |
| [14] | SEPERUELO D E, ALENCAR S H P, BATALHA C, et al. Spectrophotometric analysis of the T Tauri star GQ Lupi A[J]. Astronomy & Astrophysics, 2008, 489(1): 349–357. |
| [15] | YANG X, YI T F, ZHANG Y, et al. The γ-ray and optical variability analysis of the BL Lac object 3FGL J0449.4-4350[J]. Publications of the Astronomical Society of the Pacific, 2020, 132(1010): 1538–1548. |
| [16] | TIMMER J, KOENIG M. On generating power law noise[J]. Astronomy & Astrophysics, 1995, 300: 707–710. |
| [17] | GROSSMANN A, MORLET J. Decomposition of Hardy functions into square integrable wavelets of constant shape[J]. SIAM Journal on Mathematical Analysis, 1984, 15(4): 723–736. DOI: 10.1137/0515056 |
| [18] | FOSTER G. Wavelets for period analysis of unevenly sampled time series[J]. The Astrophysical Journal, 1996, 112(4): 1709–1729. |
| [19] | WAGNER S J, WITZEL A. Intraday variability in the BL Lac object 0954+658[J]. Astronomy & Astrophysics, 1993, 271(1): 344–347. |
| [20] | ACKERMANN M, AJELLO M, BALDINI L, et al. Fermi Gamma-ray space telescope observations of Gamma-ray outbursts from 3C 454.3 in 2009 December and 2010 April[J]. The Astrophysical Journal, 2010, 721(2): 1383–1396. DOI: 10.1088/0004-637X/721/2/1383 |
| [21] | LHTEENMKI A, VALTAOJA E, WIIK A K. Total flux density variations in extragalactic radio sources Ⅱ. determining the limiting brightness temperature for synchrotron sources[J]. The Astrophysical Journal, 2009, 511(1): 112–117. |
| [22] |
杨星, 易庭丰, 毛李胜. 平谱射电类星体B30307+380的15 GHz射电光变分析[J]. 天文研究与技术, 2020, 17(2): 1189–1196 YANG X, YI T F, MAO L S. On the 15 GHz radio variability of flat-spectrum radio quasar B30307+380[J]. Astronomical Research & Technology, 2020, 17(2): 1189–1196. |
| [23] | VALTAOJA E, TERÄSRANTA H, TORNIKOSKI M, et al. Radio monitoring of OJ 287 and binary black hole models for periodic outbursts[J]. The Astrophysical Journal, 2008, 531(2): 744–755. |
| [24] | RANI B, WIITA P J, GUPTA A C. Nearly periodic fluctuations in the long-term x-ray light curves of the blazars AO 0235+164 and 1ES 2321+419[J]. The Astrophysical Journal, 2009, 696(2): 2170–2178. DOI: 10.1088/0004-637X/696/2/2170 |
| [25] | ZHANG X, XIE G Z, BAI J M. A historical light curve of 3C 345 and its periodic analysis[J]. Astronomy & Astrophysics, 1998, 330(2): 469–473. |
| [26] | NEMMEN R S, GEORGANOPOULOS M, GUIRIEC S, et al. A universal scaling for the energetics of relativistic jets from black hole systems[J]. Science, 2012, 338(6113): 1445–1448. DOI: 10.1126/science.1227416 |
| [27] | Rieger F M. On the geometrical origin of periodicity in blazar-type sources[J]. The Astrophysical Journal Letters, 2004, 615(1): L5–L8. DOI: 10.1086/426018 |
| [28] | HENRI G, SAUGE L. The bulk Lorentz factor crisis of TeV Blazars: evidence for an inhomogeneous pileup energy distribution?[J]. The Astrophysical Journal, 2006, 640(1): 185–216. DOI: 10.1086/500039 |
| [29] | GUINEVERE K, MARTIN H. A unified model for the evolution of galaxies and quasars[J]. Monthly Notices of the Royal Astronomical Society, 2000, 311(3): 576–588. DOI: 10.1046/j.1365-8711.2000.03077.x |
| [30] | BEGELMAN M C, BLANDFORD R D, REES M J. Massive black hole binaries in active galactic nuclei[J]. Nature, 1980, 287(5780): 307–309. DOI: 10.1038/287307a0 |
| [31] | LEE W H, ABRAMOWICZ M A, KLUZNIAK W. Resonance in forced oscillations of an accretion disk and kilohertz quasi-periodic oscillations[J]. The Astrophysical Journal Letters, 2004, 603: L93–L96. DOI: 10.1086/383245 |



