2. 华中师范大学物理科学与技术学院, 湖北 武汉 430079;
3. 中国科学院新疆天文台, 新疆 乌鲁木齐 830011
2. College of Physical Science and Technology, Central China Normal University, Wuhan 430079, China;
3. Xingjiang Astronomical Observatory, Chinese Academy of Sciences, Urumqi 830011, China
脉冲星辐射束内的强度分布并不均匀,当视线扫过辐射束时,辐射流量起伏变化,形成一定形状的脉冲轮廓。但若想通过看到的轮廓来反推辐射束的结构,却非常困难。研究这一难题的途径有两个:(1)根据现象进行合理猜测,建立辐射束唯象模型,从样本统计的角度检验和修正;(2)设法直接观测脉冲星射电辐射束的二维结构。
第1个途径,目前最流行的唯象模型是20世纪80年代文[1]提出的核双锥辐射束模型。该模型是对早期的空心辐射锥模型的改进[2],认为辐射束是由较亮的核心以及外围两个嵌套的亮环组成。该模型被广泛应用于解释脉冲轮廓的多样性、偏振、子脉冲漂移等现象。
另一个模型是20世纪80年代文[3]提出的扇形辐射束模型,近10年来,扇形束模型得到了较快发展,并演变出不同的版本[4-6]。尽管具体物理机制有所不同,但这些模型都有一个共同点,即假设粒子在脉冲星磁层的磁流管中运动时产生径向延展的辐射束,形状类似扇形结构。近年来扇形束模型得到了越来越多观测现象的支持。
在这些扇形束模型中,文[5](以下简称WPZ模型)推导了辐射束的脉冲宽度和光度公式,并指出扇形束模型和锥辐射束模型的重要差别,扇形束模型预言脉冲轮廓宽度与碰撞角(观测者视线和磁轴之间的最小夹角)之间存在正相关关系,而锥辐射束模型则预言相反的关系。文[5]收集了64颗脉冲星的脉冲宽度和碰撞角数据,发现两者之间存在正相关,从而为扇形束模型提供了较强的观测支持。
第2个途径仅适用于极少数位于双星系统中的进动脉冲星,如PSR J1141-6545[7]和PSR J1906 + 0746[8]。由于自转轴的进动效应,观测者的视线能够从辐射束的不同部位扫过,从而可以观测到辐射束的二维结构。PSR J1906 + 0746的进动周期大约为160年,利用从2005~2018年跨越14年的观测数据,文[9]反演了该星辐射束的部分结构,结果显示,主脉冲和中间脉冲的辐射束均为延展的长条形,既无圆形或椭圆形的亮环,也无磁轴附近的亮斑,完全不同于核双锥模型的辐射束图像,反而更像扇形束模型的图像。PSR J1906 + 0746作为目前唯一比较可靠的具有辐射束二维结构信息的脉冲星,其偏振轮廓数据已经由Desvignes等人发布在科学数据共享网站Zenodo①上,但其辐射特征尚未在最近的文献中深入研究。
① https://zenodo.org/record/3358819
本文旨在利用开放数据挖掘PSR J1906 + 0746的辐射特征,重点比对WPZ扇形束模型的两个核心关系——脉冲宽度与碰撞角以及峰值辐射流量与碰撞角的关系。
1 数据处理该星的轮廓数据来自Zenodo,包含从2005~2018年共47个L波段平均脉冲轮廓。其中,2005~2007年是南赛(Nancay)射电望远镜的观测数据,2008~2009年以及2012~2018年是阿雷西博(Arecibo)射电望远镜的观测数据,2009~2012年无观测数据。除南赛射电望远镜的观测数据(从MJD 53572到MJD 54282)外,其他时段的流量数据均能重复文[9]的结果,因此,在分析流量特征时排除了南赛射电望远镜的观测数据。测量脉冲宽度并不需要流量定标的轮廓,因此,在分析宽度特征时采用了所有的数据。
在文[9]中,磁倾角是通过进动旋转矢量模型(Precessional RVM)拟合线偏振位置角曲线的拐点相位数据得到的。主脉冲所在磁极的磁倾角被确定为αMP=99.41° ± 0.17°,中间脉冲磁极的磁倾角αIP为αMP的补角。然后固定磁倾角,通过旋转矢量模型拟合主脉冲和中间脉冲的线偏振位置角数据得出历次观测的碰撞角。本文直接采用了文[9]支撑材料中表S2的碰撞角结果。有一个特殊情况本文做了处理,即从MJD 56963到MJD 57553(2014年11月至2016年6月),因主脉冲信噪比低而得不到碰撞角,主脉冲的碰撞角βMP需要通过中间脉冲磁极的碰撞角βIP来估算,公式为
| $ {\beta _{{\rm{MP}}}} \approx ({\alpha _{{\rm{IP}}}} + {\beta _{{\rm{IP}}}}) - {\alpha _{{\rm{MP}}}}. $ | (1) |
由于不少观测噪声明显,为了得到轮廓宽度和峰值流量密度,采用若干个高斯成分对主脉冲和中间脉冲的平均脉冲轮廓进行了拟合,得到光滑的轮廓后,再测量50%峰值宽度W50和10%峰值宽度W10(峰值高度50%和10%水平上的宽度)以及峰值流量密度fpk。有两个例外,一是MJD 57311的主脉冲轮廓因信噪比过低,不利于可靠地测量宽度和流量密度,二是从MJD 57553以后主脉冲就观测不到了,所以主脉冲宽度和峰值流量密度最后的有效数据分别为34和25个,中间脉冲对应的有效数据分别为47和38个。
脉冲宽度的误差考虑了采样间隔和高斯轮廓测量误差,总误差为二者平方和的算术平方根。所有观测的采样点都是2 048,因此,采样时间间隔对应的误差为0.18°。由于观测都采用了连续消色散的方法,色散引起的误差很小,这里不予考虑。轮廓噪声部分辐射流量密度的均方根通常在0.1 mJy左右,这个值明显低于已发表的L波段平均流量的误差[10],如果采用均方根值作为误差,很可能低估了真正的误差,因此,本文不处理辐射流量密度的误差。
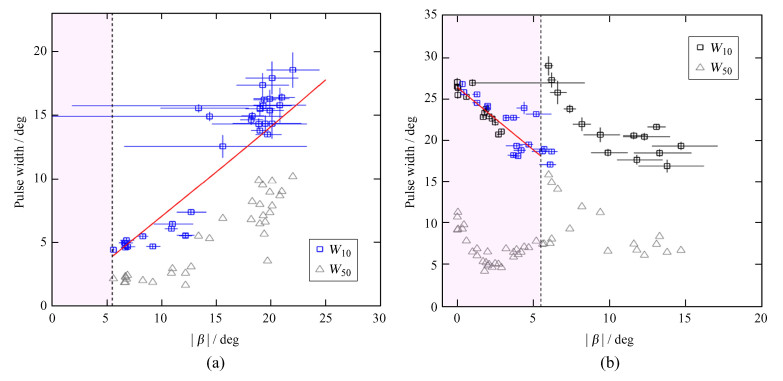
2 结果 2.1 脉冲宽度与碰撞角的关系图 1给出了主脉冲和中间脉冲的W10随
|
|
图 1 (a) 主脉冲和(b)中间脉冲的脉冲宽度随 |
WPZ模型区分了辐射束内区和外区,内区大致是从磁轴到
② 该星接近垂直转子,在磁轴和自转轴所在平面,极冠区边界的张角最小,在利用文[11]的公式(6)和(7)计算时令磁经度角φ=0;在φ=90°时张角最大。
WPZ模型指出,内外区域脉冲轮廓宽度的变化很可能不同。内区不确定性较大,在多个磁流管并存时有可能出现脉冲宽度从磁轴向外递减的情况。外区主要是偶极场磁流管的几何特征起主要作用,导致脉冲宽度W随着
| $ {\rm{cos}}\left( {\frac{W}{2} + C} \right) = \frac{{{\rm{sin}}\alpha }}{{{\rm{tan}}\left( {\alpha + \beta } \right){{({\rm{co}}{{\rm{s}}^2}\alpha + {\rm{ta}}{{\rm{n}}^{ - 2}}\varphi )}^{1/2}}}}, $ | (2) |
其中,C=tan-1(secα/tanφ);φ为磁流管边界的磁力线所具有的磁经度角。为了定义φ,先取垂直于磁轴与自转轴所在的平面为参考面,磁力线平面与该平面的二面角为磁经度角。在主脉冲一极,向下看时φ从自转方向开始沿顺时针方向递增,而在中间脉冲一极则相反,定为从自转方向开始沿逆时针方向递增。这主要是为了使两极有相同φ值的磁力线具有完全一样的与磁轴和自转方向的相对关系,便于后面比较两极的辐射束和辐射区域。
图 1(a)显示主脉冲的W10随
不过需要指出,(2)式适用的前提是辐射区关于磁轴-自转轴所在平面对称,而实际情况是主脉冲辐射束偏离磁轴和自转轴平面,朝向了自转方向一侧(见文[9]图 3),所以上述拟合只是粗略的估计。为了更好地揭示辐射束边界的磁经度分布范围,对每一个主脉冲轮廓的10%峰值强度水平上左右轮廓边界都计算了磁经度角:
| $ \varphi = \left\{ {\begin{array}{*{20}{l}} {\frac{3}{2}\pi + {\rm{sign}}\phi {\rm{co}}{{\rm{s}}^{ - 1}}\left( {\frac{{\cos\zeta - {\rm{cos}}\alpha {\rm{cos}}\rho }}{{{\rm{sin}}\alpha {\rm{sin}}\rho }}} \right)\left( {\alpha > \frac{\pi }{2}} \right)}\\ {\frac{\pi }{2} - {\rm{sign}}\phi {\rm{co}}{{\rm{s}}^{ - 1}}\left( {\frac{{{\rm{cos}}\zeta - {\rm{cos}}\alpha {\rm{cos}}\rho }}{{{\rm{sin}}\alpha {\rm{sin}}\rho }}} \right)\left( {\alpha < \frac{\pi }{2}} \right)} \end{array}} \right., $ | (3) |
|
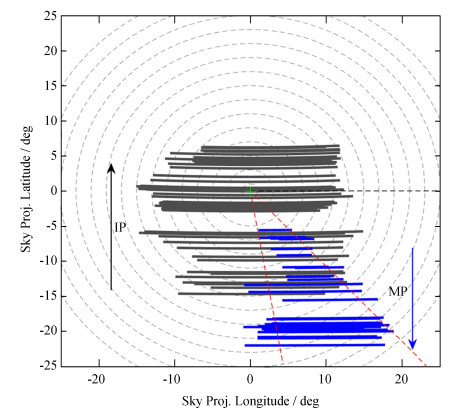
| 图 3 PSR J1906 + 0746主脉冲和中间脉冲辐射束的主要分布范围。图中显示的是天球在两个磁极(绿色十字)附近的区域,蓝色和深灰色曲线分别表示主脉冲和中间脉冲轮廓10%峰值宽度W10所对应的经度范围。为了便于比较两极的辐射束,已将主脉冲磁极区域的方位做了转换。对于主脉冲而言,从磁极(坐标原点)竖直向上指向自转轴反方向;对于中间脉冲而言,从磁极竖直指向自转轴正方向。在主脉冲和中间脉冲这两极视线的变化方向分别由蓝色和黑色箭头表示,与此相应,主脉冲的碰撞角为负值且持续减小,中间脉冲的碰撞角从正值持续变化到负值(注意图中纵坐标递增方向仅代表主脉冲碰撞角递增方向,中间脉冲的与之相反)。红色虚线表示主脉冲10%峰值强度左右边界上平均磁经度角 Fig. 3 The major ranges of the main-pulse and interpulse emission beams of PSR J1906 + 0746. The area of the celestial sphere near the two magnetic poles (green cross) is shown. The blue and dark-gray curves represent the projection of the longitudinal ranges for W10 of the main pulse and the interpulse, respectively. In order to compare the emission beams between the two poles, the orientation of the main-pulse polar region has been adjusted. For the main pulse, the direction pointing from the pole (coordinate origin) vertically upwards represents the opposite direction of rotation axis, while for the interpulse, it represents the positive direction of the rotation axis. The directions of the line of sight at the main-pulse and interpulse poles are represented by blue and black arrows, respectively. Accordingly, the impact angle of the main pulse is negative and decreases continuously, and the impact angle of the interpulse changes continuously from positive to negative values (note that the increment direction of the ordinate only represents the increment direction of the impact angle for the main pulse, while it is opposite to the interpulse). The red dotted lines represent the average magnetic longitudes on the left and right boundaries at the 10% peak intensity level of the main-pulse profile |
其中,视线角ζ为视线与自转轴的夹角,满足ζ=α + β;ρ为相对轮廓参考中心的相位
| $ \rho = {\rm{co}}{{\rm{s}}^{ - 1}}({\rm{cos}}\zeta {\rm{cos}}\alpha + {\rm{sin}}\zeta {\rm{sin}}\alpha {\rm{cos}}\phi ), $ | (4) |
其中,
文[9]采用旋转矢量模型最佳拟合曲线的拐点确定主脉冲和中间脉冲的中心参考相位,将它们设置为0°和180°,用以对齐轮廓。Zenodo共享的轮廓数据已经进行了相位对齐,但中心相位并不是0°和180°,Zenodo的技术文档也未说明中心参考相位在哪里。通过与文[9]中轮廓的比对,确定主脉冲和中间脉冲轮廓的中心参考相位分别近似为0.25和0.75(以自转周期为单位)。随后,主脉冲的相位和中间脉冲的相位分别减去上述值,归算出相对相位
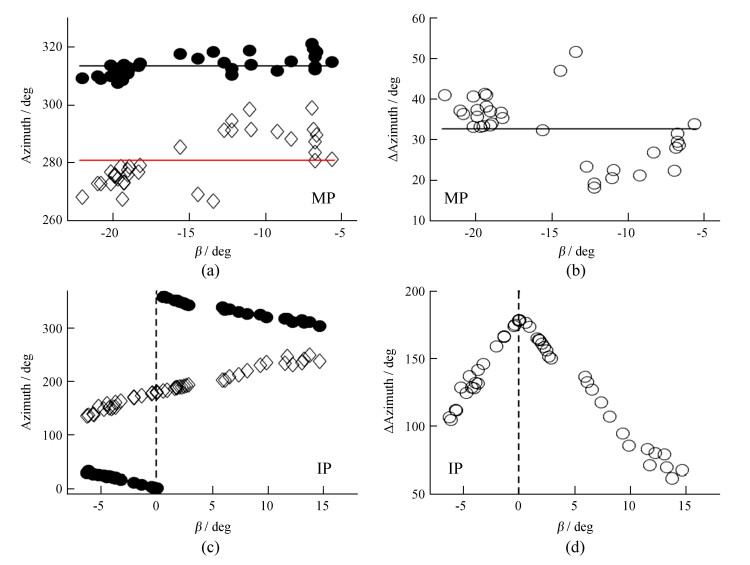
图 2(a)给出了主脉冲10%峰值强度边界的磁经度角随碰撞角的变化。可以看到,主脉冲的左边界和右边界都在各自的平均值附近摆动,二者之差所得的磁经度宽度为Δφ=33° ± 8°(见图 2(b)),这与之前利用(2)式拟合得到的结果差别不大。
|
| 图 2 PSR J1906 + 0746脉冲轮廓10%峰值强度辐射束边界的磁经度角(“Azimuth”,即φ)和辐射束磁经度宽度(“Δ Azimuth”,即Δφ)。(a)不同碰撞角时主脉冲(MP)的辐射束左边界(菱形)和右边界(圆点)的φ,红色和黑色水平线表示平均磁经度角,分别是左边界281°和右边界313°。(b)主脉冲辐射束的Δφ。(c)和(d)分别是中间脉冲(IP)的φ和Δφ,其中,(c)图中在β=0处右边界φ值的跳变是由于随着时间变化β从正值变到负值,右边界从第四象限变到第一象限所致,见图 3。磁经度角根据脉冲轮廓10%峰值水平的左右边界相位计算得到,其计量方法见正文和图 1。因主脉冲近期观测不到或信噪比过低,在2005~2018年的47次观测中,主脉冲共有34个轮廓可用,中间脉冲共有47个轮廓 Fig. 2 The magnetic longitude ('Azimuth', i. e. φ) and the magnetic longitude width of the emission beam ('ΔAzimuth', i. e. Δφ) at the 10% peak intensity level of the pulse profile of PSR J1906 + 0746. (a) The φ of the left boundary (diamonds) and the right boundary (dots) of the emission beam of the main pulse (MP) for different impact angle. The red and black horizontal lines represent the average magnetic longitudes, which are 281° for the left boundary and 313° for the right boundary, respectively. (b) The Δφ of the main pulse emission beam. (c) and (d) are φ and Δφ of the interpulse (IP), respectively. In panel (c), the jump of φ value of the right boundary at β=0 is caused by the change of the right boundary from the fourth quadrant to the first quadrant when β changes from a positive value to a negative value, as shown in Figure 3. The magnetic longitude is calculated according to the left and right boundary phases at the 10% peak intensity level of the pulse profile. See text and Figure 1 for its measuring method. Because the main pulse was not detected or the signal-to-noise ratio is too low in recent observations, in the 47 observations in 2005-2018, 34 profiles of the main pulse are useful. 47 profiles of the interpulse are useful |
为了更加直观地显示辐射束结构,将主脉冲的磁经度角范围投影到天球上,在图 3中用蓝色线段表示,同时用蓝色箭头表示碰撞角随观测时间的变化方向。可见在主脉冲磁极,辐射束主要位于第四象限。两条红色虚线分别表示左边界和右边界的平均磁经度角。如图 3,主脉冲辐射束能较好地用红色边界线之间的辐射束描述。
需要特别指出,这里采用每个轮廓10%峰值强度的轮廓边界表征辐射束边界,可以理解为对各轮廓独立做强度归一化,然后做相对强度10%水平上的等值图,而文[9]的图 3则是用绝对流量做等值图,二者效果不同。当辐射束内部流量密度差别巨大时,绝对流量的等值图不利于完整地显示弱的结构,而采用相对强度等值图则更有优势。对比本文图中纵坐标-15°以下的部分和文[9]图 3主脉冲辐射束的相同部分,可以非常清楚地看到这一点。
相比主脉冲,中间脉冲表现出截然不同的脉冲宽度与碰撞角的相关性,如图 1(b)。在辐射束内区,W10与
图 2(c)给出了中间脉冲10%峰值强度辐射束边界的磁经度角随碰撞角的变化。可以看到左右边界均出现持续变化,而不像主脉冲那样在各自平均值附近摆动。图 2(d)显示,随着碰撞角由正值变为负值,辐射束磁经度宽度先逐渐增大,在碰撞角为0°,即视线扫过磁轴时,磁经度宽度达到最大值180°,随后减小。这表明中间脉冲辐射束并不是固定宽度的磁流管产生的,而是在环绕极轴的磁力线上产生的,这可以直观地从图 3中深灰色的辐射束投影区域看出来。就磁经度范围的这一特点而言,中间脉冲辐射束更具有锥辐射束的特点,但是辐射束在纬度方向的延展性是锥辐射束模型无法解释的。
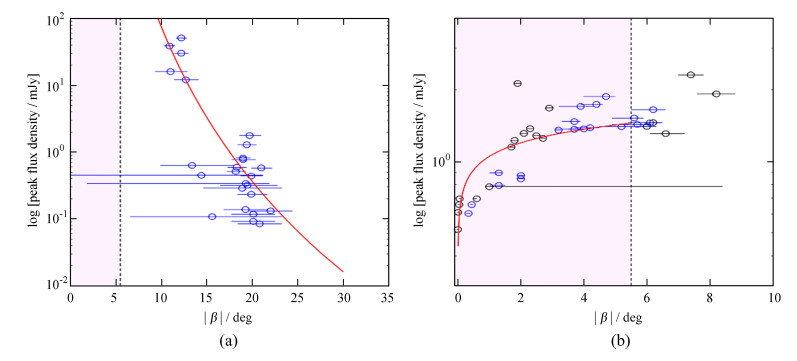
2.2 辐射流量密度与碰撞角的关系图 4显示了峰值流量密度与
| $ {f_{{\rm{pk}}}} \approx AP{^{q - 4}}{\dot P_{ - 15}}{\left| \beta \right|^{2q - 6}}, $ | (5) |
|
|
图 4 (a) 主脉冲和(b)中间脉冲轮廓峰值流量密度与 |
其中,
如图 4(b),中间脉冲的峰值流量密度与
由于PSR J1906 + 0746两极的辐射束都明显不符合核双锥辐射束的图像,因此,这里不讨论核双锥模型,而重点讨论扇形束模型。从上述结果可以看到,WPZ扇形束模型能够符合一部分观测特征,也有不符合的,分别概括和讨论如下:
(1) WPZ模型可以定量解释的观测事实
① 主脉冲的脉冲宽度和
② 主脉冲的轮廓峰值流量密度与
(2) 难以用WPZ模型解释的观测特征
① 中间脉冲宽度随
② 中间脉冲辐射束外区峰值脉冲流量的整体趋势随
③ 中间脉冲的辐射来自磁轴四周,辐射束跨越磁轴延展,这对WPZ模型来说是个难题。主脉冲的辐射束是否也具有跨越磁轴的性质尚无数据支持,但从文[9]发表的辐射束来看,1998年所看到的脉冲比较宽,离磁轴较近,且位于磁轴的另一侧,与主要的辐射束相对,所以不能排除其辐射束类似中间脉冲辐射束那样跨越磁轴延展的可能。
WPZ模型的困难主要来自其现有的假设,认为辐射束是由单个或若干分立的磁流管产生的子辐射束构成的,每一个子辐射束都是延展的扇叶形或长条形,其末端汇聚在磁轴(见文[5]图 5~图 8),这样就不能形成像中间脉冲那样连贯的跨越磁轴的条形辐射束。
其他的扇形束模型,如文[4, 6, 12]的工作,均未明确给出辐射束的宽度、辐射流量与碰撞角的关系,且通常假设辐射束内边缘离磁轴有一段距离,所以对磁轴附近的辐射也缺乏考虑。
3.2 扇形束模型改进的方向中间脉冲辐射束的特征要求一种兼具锥模型和扇形束模型特点的唯象模型,需满足以下几个要素:
(1) 图 2(d)的结果要求辐射能够从各个磁经度角的磁力线上产生,例如极冠区内围绕磁轴的一圈磁力线,或者整个极冠区等,这一点类似于锥辐射束模型常用的假设。
(2) 文[9]的结果表明,在相差很大的辐射高度上都可以产生1.4 GHz波段的辐射,这不符合通常认为的不同频率的辐射来自不同高度的假设。更加合理的假设是相对论性粒子流在沿磁力线外流过程中产生宽频辐射,因而在单个频率上看辐射束可以是足够延展的。
(3) 在上述两个假设的前提下,如果辐射强度随高度的变化关系不依赖于磁经度角,势必会导致圆形的辐射束结构。但观测到中间脉冲辐射束的形状在纬度方向延展,在经度方向相对压缩,因而就要求辐射强度与高度的关系在不同的磁经度角上有差异,以便能够解释这种长条形的特征。
采取以上假设,通过调节模型参数,理论上有可能构建出具有PSR J1906 + 0746辐射束特征的唯象模型,这对构建更加深入的辐射模型具有借鉴意义。
3.3 关于磁轴附近辐射的物理机制如何解释PSR J1906 + 0746磁轴附近的辐射是构建辐射模型的重要内容之一。曲率辐射经常用于解释脉冲星射电辐射[13-14]。在静态磁偶极场模型下,磁轴上的磁力线曲率为0,附近的开放磁力线曲率也非常小,因此,无法通过曲率辐射产生有效的射电辐射。但在旋转磁偶极场情况下,磁力线的曲率会增大,是否足以产生观测到的射电辐射频率和流量,需要具体研究。
逆康普顿散射模型[15-16]在这方面可能更有优势。该模型下,极冠加速区放电产生的低频电磁波在向外传播时被次级相对论性粒子散射(逆康普顿散射过程),产生较高频率的射电波。只要低频波波矢方向和次级粒子运动方向的夹角不为0,散射过程便可发生。当磁轴附近有次级粒子外流时,它们同其他区域产生的低频波散射满足夹角不为0的条件,便可能产生可观测的射电辐射。
无论是曲率辐射模型还是逆康普顿散射模型,都要求从磁轴附近有相对论性次级粒子外流。在内加速区模型框架下[13],要求在磁轴附近的极冠加速区存在多极磁场,以提供足够大的磁力线曲率,使得级联放电过程能够发生。
3.4 两极辐射束的差异性一般认为,脉冲星两极的磁场结构应该是相同的,在相同磁场结构的区域,物理过程也是相同的,因而两极的辐射束结构应该相同。图 3将两极的辐射束重叠比较,在相同的象限,两极的磁场结构是相同的。然而,主脉冲和中间脉冲辐射束却相差甚大,即便是在视线都扫过的区域,二者的磁经度范围也差别很大,中间脉冲的辐射区域明显要宽得多。需要注意的是,根据文[9],1998年时主脉冲的位置在本文图 3中位于纵坐标接近5°的地方,且脉冲轮廓的中心接近横坐标0°,因此,不排除主脉冲的辐射束也跨越磁轴,辐射也来自环绕磁轴的磁力线的可能性。即便如此,两极的辐射束形状的差异仍然十分显著。这一点在文[9]中未引起足够重视,而PSR J1906 + 0746作为第1颗能揭示两极辐射差异性的脉冲星,对通常的观点构成了挑战。
两极辐射束在形状方面的差异,既可能是辐射来源的磁力线分布不同,也可能是两极的磁场结构不同。关于第1种可能性,可以利用旋转磁偶极模型的辐射几何,从观测数据中尝试反演两极辐射的来源区域,检查磁力线分布的可能差异及其合理性。关于第2种可能性,文献中有少数工作曾提出两个磁极不平行的理论模型[17-18],其中两极的物理性质可能会有差异,这提供了一种思路。这样的模型中两个极轴的相位会偏离180°,且线偏振位置角曲线偏离经典的旋转矢量模型,因此需要建立模型,通过拟合偏振观测数据来探索可能的参数空间,进而判断这种模型的可行性。这两种模型的主要差别之一是线偏振位置角曲线和两个磁极的相位差,因此,需要综合两极的数据对全周期的线偏振位置角进行完整的拟合,尝试是否可以区分两者。如果这两种模型都能在合理的参数空间解释偏振观测特征,则需要进一步考虑解释两极辐射束内强度分布特征差异的可行性,不过这可能高度依赖具体的辐射模型。
4 结论本文利用PSR J1906 + 0746的开放数据,研究了该星的主脉冲和中间脉冲的辐射特征。结果表明,主脉冲的10%峰值强度脉冲宽度和
| [1] | RANKIN J M. Toward an empirical theory of pulsar emission. I. morphological taxonomy[J]. The Astrophysical Journal, 1983, 274: 333–358. DOI: 10.1086/161450 |
| [2] | KOMESAROFF M M. Possible mechanism for the pulsar radio emission[J]. Nature, 1970, 225(5233): 612–614. DOI: 10.1038/225612a0 |
| [3] | MICHEL F C. A pulsar emission model:observational tests[J]. The Astrophysical Journal, 1987, 322: 822. DOI: 10.1086/165775 |
| [4] | DYKS J, RUDAK B, DEMOREST P. The nature of pulsar radio emission[J]. Monthly Notices of the Royal Astronomical Society, 2010, 401(3): 1781–1795. DOI: 10.1111/j.1365-2966.2009.15679.x |
| [5] | WANG H G, PI F P, ZHENG X P, et al. A fan beam model for radio pulsars. I. observational evidence[J]. The Astrophysical Journal, 2014, 789(1): 73. DOI: 10.1088/0004-637X/789/1/73 |
| [6] | DYKS J, RUDAK B. The origin of the frequency-dependent behaviour of pulsar radio profiles[J]. Monthly Notices of the Royal Astronomical Society, 2015, 446(3): 2505–2522. DOI: 10.1093/mnras/stu2262 |
| [7] | MANCHESTER R N, KRAMER M, STAIRS I H, et al. Observations and modeling of relativistic spin precession in PSR J1141-6545[J]. The Astrophysical Journal, 2010, 710(2): 1694–1709. DOI: 10.1088/0004-637X/710/2/1694 |
| [8] | DESVIGNES G, KRAMER M, COGNARD I, et al. PSR J1906+0746: from relativistic spin-precession to beam modeling[C]//Proceedings of the IAU Symposium. 2013: 199-202. |
| [9] | DESVIGNES G, KRAMER M, LEE K, et al. Radio emission from a pulsar's magnetic pole revealed by general relativity[J]. Science, 2019, 365(6457): 1013–1017. DOI: 10.1126/science.aav7272 |
| [10] | LORIMER D R, STAIRS I H, FREIRE P C, et al. Arecibo pulsar survey using ALFA. II. the young, highly relativistic binary pulsar J1906+0746[J]. The Astrophysical Journal, 2006, 640(1): 428–434. DOI: 10.1086/499918 |
| [11] | LEE K J, DU Y J, WANG H G, et al. Low bounds for pulsar γ-ray radiation altitudes[J]. Monthly Notices of the Royal Astronomical Society, 2010, 405(3): 2103–2112. |
| [12] | OSWALD L, KARASTERGIOU A, JOHNSTON S. Understanding the radio beam of PSR J1136+1551 through its single pulses[J]. Monthly Notices of the Royal Astronomical Society, 2019, 489(1): 310–324. DOI: 10.1093/mnras/stz2121 |
| [13] | RUDERMAN M A, SUTHERLAND P G. Theory of pulsars-polar caps, sparks, and coherent microwave radiation[J]. The Astrophysical Journal, 1975, 196: 51–72. DOI: 10.1086/153393 |
| [14] | WANG P F, WANG C, HAN J L. Curvature radiation in rotating pulsar magnetosphere[J]. Monthly Notices of the Royal Astronomical Society, 2012, 423(3): 2464–2475. DOI: 10.1111/j.1365-2966.2012.21053.x |
| [15] | QIAO G. A mechanism for core emission of pulsars[J]. Vistas in Astronomy, 1988, 31(1): 393–397. |
| [16] | QIAO G J, LIN W P. An inverse Compton scattering (ICS) model of pulsar emission. I. core and conal emission beams[J]. Astronomy and Astrophysics, 1998, 333: 172–180. |
| [17] | HARDING A K, MUSLIMOV A G. Pulsar pair cascades in magnetic fields with offset polar caps[J]. The Astrophysical Journal, 2011, 743(2): 181. DOI: 10.1088/0004-637X/743/2/181 |
| [18] | BURNETT C R, MELATOS A. Stokes tomography of a radio pulsar with an offset magnetic dipole[J]. Monthly Notices of the Royal Astronomical Society, 2014, 440(3): 2519–2527. DOI: 10.1093/mnras/stu073 |



