法拉第旋转(Faraday Rotation)是线偏振电磁波通过磁化星际介质时偏振角发生旋转的一种物理现象。偏振位置角旋转的大小可以写成ϕ(
| $ \phi \left( {\vec r} \right) = \int_r^{{\rm{observer}}} {{n_{\rm{e}}}{B_\parallel }{\rm{d}}l} , $ | (1) |
其中,ne为热电子密度;B‖为视线方向的磁场分量;dl是视线方向上的线元。这样观测到的偏振量P可以写成[1]:
| $ P\left( {{\lambda ^2}} \right) = Q\left( {{\lambda ^2}} \right) + iU\left( {{\lambda ^2}} \right) $ | (2) |
| $ = \int_{ - \infty }^\infty {F\left( \phi \right)\exp \left( {2i\phi {\lambda ^2}} \right){\rm{d}}\phi } , $ | (3) |
其中,F(ϕ)为法拉第色散函数(Faraday Dispersion Function),是法拉第深度的函数;Q和U为斯托克斯参量,是观测波长(频率)的函数。从(3)式可以看出,偏振量P和法拉第色散函数F(ϕ)之间是傅里叶变换对。F(ϕ)表示法拉第深度为ϕ处的偏振强度和偏振位置角,反映辐射区域以及辐射传播途径上的磁场结构。为了研究星际介质的磁场,需要重构法拉第色散函数。目前已有多种重构法拉第色散函数的方法。文[1]提出了法拉第旋率综合方法(Faraday Rotation Measure Synthesis, RMS),通过观测偏振量和法拉第色散函数之间的傅里叶关系重构法拉第色散函数。因为观测波段是有限的,所以获得的法拉第色散函数是真实色散函数与窗口函数的卷积,对复杂的源需要解卷积。与法拉第旋率综合方法类似的还有小波方法[2-3]。此外,还有一些假定辐射模型的方法重构法拉第色散函数,如Q-U拟合法[4]。
本文主要讨论压缩感知方法(或称为压缩采样,Compressive Sensing/Sampling,原理见[5-6])。该方法的优点在于利用极少的采样数据也有可能重构原始的完整信号。压缩感知理论以信号的稀疏性为前提,通过编码测量和重构算法实现信号的精确重构。目前,已经提出了基于压缩感知法的法拉第色散函数重构算法,如文[7]采用最小l1范数法建立了适用于法拉第薄源(Faraday Thin,λ2Δϕ << 1,这里Δϕ为源在法拉第深度域上的延展范围,即F(ϕ)的宽度)、法拉第厚源(Faraday Thick, λ2Δϕ >> 1)和同时含有法拉第薄源和法拉第厚源的算法,模拟结果显示,该方法可以用于重构法拉第色散函数,并与法拉弟旋率综合方法进行比较,发现用压缩感知方法重构的法拉第色散函数在数值和误差上要优于法拉弟旋率综合方法。文[8]采用匹配追踪算法建立了对同时含有法拉第薄源和法拉第厚源进行重构的方法。但这些方法目前还处于理论模拟阶段,其实用性还有待研究,比如文[7]的算法中设置的频率(波长)范围过大,未将噪声添加到实验数据中,算法中各种参数设置对重构结果的影响也没有进行实验和讨论以及实验样本过少等。本文基于文[7]的方法,从实际观测角度进行数值模拟,对以上问题进行更深入研究,以此探讨其实用性。这里假定法拉第色散函数是稀疏的(即针对源包含一个或多个法拉第薄成分),用Python语言编写了重构法拉第色散函数的程序。采用的频率范围为1.1~3.1 GHz,对应澳大利亚望远镜致密阵(Australia Telescope Compact Array, ATCT)上L波段的观测频率范围[9]。
1 重构方法已知测量矩阵 A ∈RM × N (M << N)和未知信号x0在该矩阵的线性投影y ∈RM,即y=Ax0,要由测量值y重构未知信号x0。在压缩感知理论中,假定未知信号x0为稀疏的,信号x0可以由测量值y通过求解最小l1范数问题精确重构:
| $ \mathit{\boldsymbol{x}} = \min {\left\| {{\mathit{\boldsymbol{x}}_0}} \right\|_{{l_1}}}s.\;t.\;\;\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_0} = \mathit{\boldsymbol{y}}. $ | (4) |
若未知信号 x0为非稀疏的,可以通过某种变换(如小波变换)进行稀疏性表示,即 x0=ωX,X为该信号在ω变换域下的稀疏性表示,则有
| $ \mathit{\boldsymbol{x}} = \min {\left\| \mathit{\boldsymbol{X}} \right\|_{{l_1}}}\;s.\;t.\;\;\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_0} = \mathit{\boldsymbol{A\omega X}} = \mathit{\boldsymbol{y}}. $ | (5) |
将(2)式写成矩阵形式:
| $ \mathit{\boldsymbol{Yf}} = \mathit{\boldsymbol{P}}, $ | (6) |
其中,f为法拉第色散函数,是一个N维矢量;Y为P和f之间傅里叶变换的离散表示,是一个M × N矩阵;P为观测偏振量,是一个M维矢量,这里M为观测频率通道数,每个通道上接收不同波段的偏振量。
由于法拉第色散函数 f是复变函数,可以将其实部和虚部分别写成f. real和f. imag,则(6)式可变为
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{C}}&{ - \mathit{\boldsymbol{S}}}\\ \mathit{\boldsymbol{S}}&\mathit{\boldsymbol{C}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}}.real}\\ {\mathit{\boldsymbol{f}}.imag} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}}.real}\\ {\mathit{\boldsymbol{P}}.imag} \end{array}} \right], $ | (7) |
其中,C和S都是M × N矩阵,Cij=cos2ϕjλi2,Sij=sin2ϕjλi2, i=1, 2, …, M, j=1, 2, …, N;
将观测通道数M设置为100,波长范围为0.096 m到0.273 m (对应频率1.1~3.1 GHz),为了更好地描述实验设置,引用文[1]中的两个定义:最大法拉第深度|ϕmax|和法拉第旋率传播函数(RMSF)的半峰全宽(FWHM) ΔϕFWHM,这两个量由最大波长的平方λmax2、最小波长的平方λmin2和观测通道的间隔(即两个相邻波长平方的间隔) δλ2决定:
| $ \left| {{\phi _{\max }}} \right| = \frac{{\sqrt 3 }}{{\delta {\lambda ^2}}}, $ | (8) |
| $ \Delta {\phi _{{\rm{FWHM}}}} = \frac{{2\sqrt 3 }}{{\lambda _{\max }^2 - \lambda _{\min }^2}}. $ | (9) |
实验中,将均值为0、标准差σ为1 (强度单位任意,下同)的高斯噪声加到Q和U上,并设置在法拉第深度ϕ空间的分辨率δϕ为ΔϕFWHM的1/4,则总的格点数N (ϕ空间中坐标点ϕi的个数,i=1, 2, …, N)为
| $ N = {\mathop{\rm int}} \left( {\frac{{2\left| {{\phi _{\max }}} \right|}}{{\delta \phi }}} \right), $ | (10) |
其中,int()表示取整。表 1列出了一些主要的实验参数。
| λmax2 | 9.2 × 10-3 m2 |
| λmin2 | 7.5 × 10-2 m2 |
| δλ2 | 6.6 × 10-4 m2 |
| |ϕmax| | 2 625 rad·m-2 |
| ΔϕFWHM | 53 rad·m-2 |
| N | 384 |
| δϕ | 13.7 rad·m-2 |
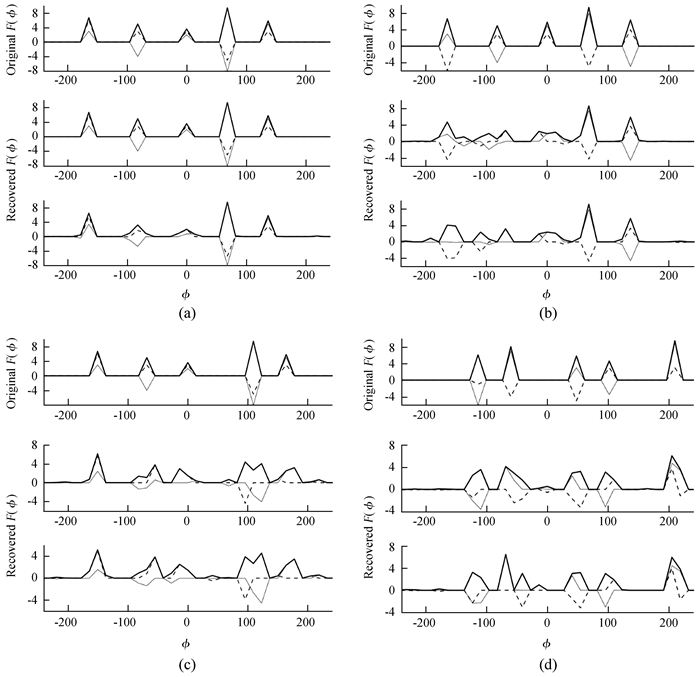
在模拟实验中,假定一个法拉第色散函数包含5个法拉第薄源, 这些源分别是:F(-164.1)=3 + 6i,F(-82.0)=-4 + 3i,F(0.0)=2 + 3i,F(68.4)=-8 - 5i,F(136.7)=5 + 3i,对应的信噪比分别为:6.7,5.0,3.6,9.4,5.8。对包含这5个法拉第薄源的法拉第色散函数进行了反解,结果如图 1 (a),这里采用ϕ的加权平均的差值(dwm)比较重构函数
| $ \left| {{d_{{\rm{wm}}}}} \right| = \left| {\sum\limits_{i = 1}^N {{p_i}{\phi _i}} /\sum\limits_{i = 1}^N {{p_i}} - \sum\limits_{i = 1}^N {{{\tilde p}_i}{{\tilde \phi }_i}} /\sum\limits_{i = 1}^N {{{\tilde p}_i}} } \right|, $ | (11) |
|
| 图 1 法拉第色散函数的重构结果。每幅图从上往下,上图为原始数据,中图为无噪声重构结果,下图为有噪声重构结果,粗实线表示振幅,细实线表示实部,细虚线表示虚部 Fig. 1 The reconstruction result of Faradqy dispersion function. From top to bottom in each panel: the original data, the noiseless reconstruction result and the with-noise reconstruction result. The thick solid line shows the amplitude, the thin solid line as real part, the dashed line as imaginary part |
其中,p为偏振强度。从图 1可以看出,没有噪声时该模型准确地重构了原始图像,而加入噪声时,重构结果出现了偏差,|dwm|分别为5.80 × 10-5,11.78。
通过压缩感知方法重构的法拉第色散函数随着法拉第薄源偏振强度的大小、相位以及两个法拉第薄源的法拉第深度之间间隔Δϕ的不同而不同,甚至不能准确地重构出原始图像。在这里分两种情况进行测试说明:(1)假定上述5个法拉第薄源的法拉第深度之间的间隔Δϕ不变,改变其大小和相位,如F(-164.1)=3 - 6i,F(-82.0)=-4 + 3i,F(0.0)=5 + 3i,F(68.4)=8 - 5i, F(136.7)=-5 + 4i,对应的信噪比分别为:6.7,5.0,5.8,9.4,6.4,重构结果如图 1 (b);(2)假定大小和相位不变,改变其法拉第深度之间的间隔Δϕ,如:F(-150.4)=3 + 6i,F(-68.4)=-4 + 3i,F(0.0)=2 + 3i,F(109.4)=-8 - 5i,F(164.1)=5 + 3i,对应的信噪比分别为6.7,5.0,3.6,9.4,5.8,重构结果如图 1 (c)。
当假定间隔Δϕ不变时,从图 1可以看出,前3个源并没有很好地重构出原始图像,其相位和大小存在一定误差,其中,|dwm|分别为6.31,17.03。而假定大小和相位不变时,后面4个源都与原始图像出现了较大偏差,其中,|dwm|分别为8.18,17.11。同时也发现,在不加入噪声时,将这些法拉第薄源的法拉第深度之间的间隔Δϕ设置得足够大时,即Δϕ > 90 rad·m-2时,无论改变其大小、相位还是间隔Δϕ,该模型均能准确地重构原始图像,即使在加入噪声时,产生的误差也很微小。当然,以上测试的这些源的法拉第深度都是设置在该方法的格点N上进行的。
通常,在实际应用中,事先并不知道法拉第色散函数的法拉第深度以及两个源的法拉第深度之间的间隔Δϕ,要重构的法拉第色散函数各个成分的法拉第深度是随机的,一般不在这种方法设置的格点N上,并且Δϕ也是随机的,所以也无法确定该模型是否能够很好地重构法拉第色散函数。随机选取一个包含5个法拉第薄源的色散函数(这些法拉第薄源的法拉第深度不在格点N上):F(-114)=-6 - 1i,F(-60)=7 - 4i,F(48)=3 - 5i,F(102)=-3.5 + 3i,F(210)=9 + 3i,对应的信噪比分别为:6.1,8.1,5.8,4.6,9.5。其测试结果如图 1 (d),其中,|dwm|分别为0.40,10.20。
每次模拟都是随机产生的高斯噪声,所以每次重构的结果不同。在实验中,对于法拉第色散函数的重构结果随着源的个数、大小、相位和噪声的不同出现不同程度的误差,同时也与该方法中设置的参数有关,如观测通道M,ϕ空间的分辨率δϕ。
2.2 大样本实验为了更直观地观察该方法的重构效果,从噪声、两个源的法拉第深度之间的间隔Δϕ、ϕ空间的分辨率δϕ (δϕ的不同会导致总的格点数N不同) 3方面对重构结果的影响分别进行了大样本统计学实验。以重构的源的数目和ϕ的加权平均的差值描述重构结果的好坏[10]。
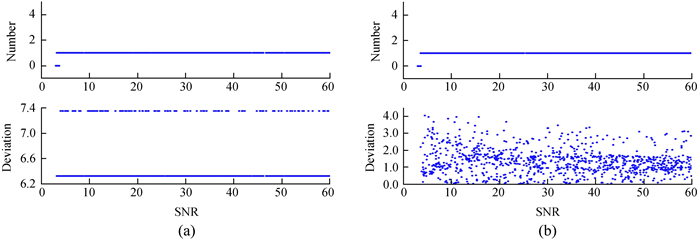
首先考察信噪比对重构结果的影响,这里假定法拉第色散函数只包含一个法拉第薄源,固定其法拉第深度为ϕ=20 rad·m-2,随机模拟了1 000个信噪比范围在(3, 60)之间的源(这里噪声依然设置为1,信噪比相当于法拉第色散函数的偏振强度),ϕ空间的分辨率δϕ依然为ΔϕFWHM的1/4,由于只含有一个法拉第薄源,直接以ϕ的差值|ϕrecorved-ϕoriginal|描述重构效果,并排除信噪比小于2的信号。结果如图 2 (a)。从图中可以看出,对于含有一个源的情况,可以很准确地重构出源的数目,而ϕ的差值总是在两个值上,即重构的ϕrecorved出现在相邻的两个格点上。为了减小重构误差,对重构结果在峰值附近进行最小二乘拟合,结果如图 2 (b)。经过拟合后,对于大多数源来说,ϕ的差值缩小为原来的1/2~1/4。由于重构的法拉第深度ϕ总在相邻的两个格点上,是否也可以通过缩小ϕ空间分辨率的方式减小ϕ的重构误差呢?
|
| 图 2 从左到右为(a)无拟合;(b)拟合后。每幅图从上往下,上为重构数目,下为ϕ的差值 Fig. 2 From left to right: (a) no fitting; (b) fitting. From top to bottom in each panel: the number of reconstructions, the difference of ϕ |
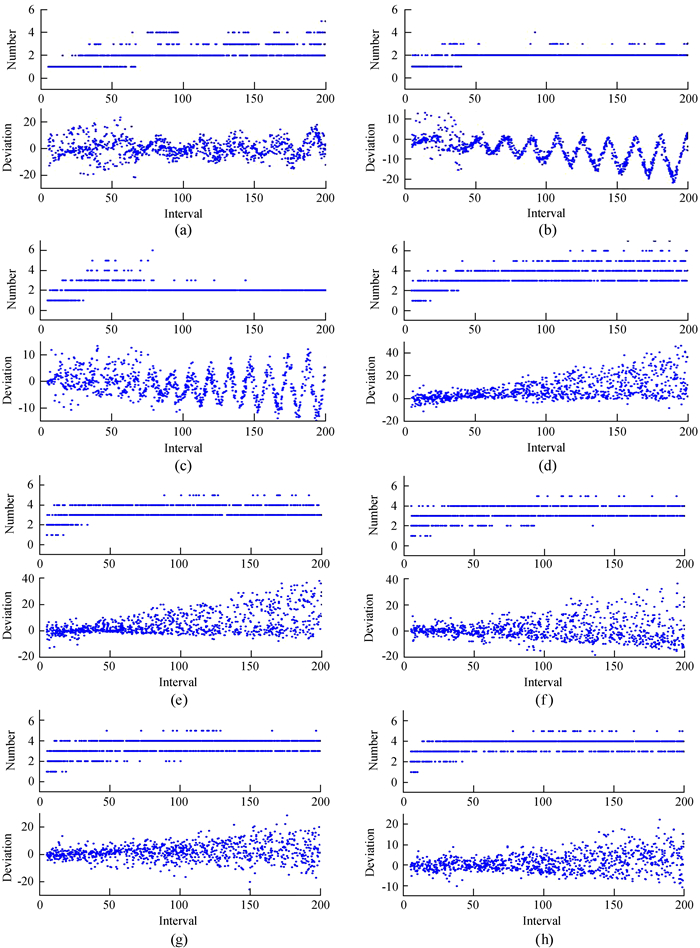
下面考查两个源的法拉第深度之间的间隔Δϕ和ϕ空间的分辨率δϕ对重构结果的影响。假定一个法拉第色散函数包含2个法拉第薄源,固定其中一个源的偏振强度p=13.235,偏振位置角χ=2.749,法拉第深度ϕ=10.256 rad·m-2。第2个源是随机模拟了1 000个偏振强度在(3, 30)、偏振位置角在(0, 2π)、间隔Δϕ在(5, 200)之间的源。同时,对不同分辨率δϕ的情况(即δϕ取ΔϕFWHM的1/2,1/3,1/4,1/5,1/6,1/7,1/8,1/9)分别进行以上实验,这里排除信噪比小于1的信号。结果如图 3。
|
| 图 3 不同分辨率下间隔Δϕ对重构结果的影响。第1排从左到右为(a) δϕ取ΔϕFWHM的1/2;(b) δϕ取ΔϕFWHM的1/3;第2排从左到右为(c) δϕ取ΔϕFWHM的1/4;(d) δϕ取ΔϕFWHM的1/5;第3排从左到右为(e) δϕ取ΔϕFWHM的1/6;(f) δϕ取ΔϕFWHM的1/7;第4排从左到右为(g) δϕ取ΔϕFWHM的1/8;(h) δϕ取ΔϕFWHM的1/9。每幅图从上往下,上为重构数目,下为ϕ的加权平均的差值dwm Fig. 3 Influence of the interval Δϕ at different resolutions. From left to right in first row: (a) δϕ takes 1/2 of ΔϕFWHM; (b) δϕ takes 1/3 of ΔϕFWHM, in second row: (c) δϕ takes 1/4 of ΔϕFWHM; (d) δϕ takes 1/5 of ΔϕFWHM, in third row: (e) δϕ takes 1/6 of ΔϕFWHM; (f) δϕ takes 1/7 of ΔϕFWHM, in fourth row: (g) δϕ takes 1/8 of ΔϕFWHM; (h) δϕ takes 1/9 of ΔϕFWHM. From top to bottom in each panel: the number of reconstructions, the difference (dwm) of the weighted average of ϕ |
为了比较不同分辨率情况下的重构效果,对不同分辨率下准确重构出源的数目的精确度进行了比较,如图 4。从图 4可以看出,当δϕ取ΔϕFWHM的1/3和1/4时,精确度最高,达到83%左右。在以上对噪声影响的实验时,曾提出是否可以通过缩小分辨率的方式减小重构误差的问题,而在这个实验中可以看出,分辨率δϕ并不是越小越好。

|
| 图 4 不同分辨率下的重构精度比较。x轴表示δϕ /ΔϕFWHM的比值,y轴表示重构数目的精确度 Fig. 4 Comparison of reconstruction accuracy at different resolutions. X-axis represents the ratio of δϕ /ΔϕFWHM, and Y-axis represents the accuracy of the number of reconstructions |
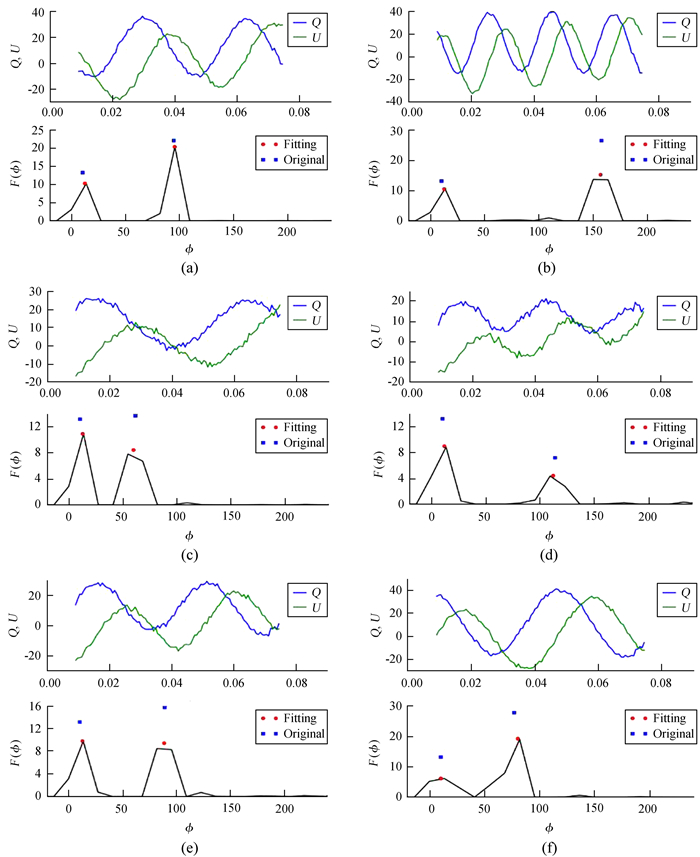
以δϕ取ΔϕFWHM的1/4时为例,随机选取几幅重构图像,如图 5。从图 5可以看出,对重构图像进行最小二乘拟合后的法拉第深度ϕfitting更接近于输入模型的法拉第深度ϕoriginal,但拟合(或重构)出的源的偏振强度pfitting都要低于输入模型的源的偏振强度poriginal。由图 5 (c)可以看出,两个源的间隔Δϕ > 50时,dwm随着间隔Δϕ的增大呈现一个周期性振荡。出现这种振荡的原因可能与第2个源的法拉第深度的位置有关。为此,在dwm随着间隔Δϕ变化的图上分别标记了当第2个源在格点ϕi,
|
| 图 5 以δϕ取ΔϕFWHM的1/4时实验为例,随机选取的重构图像 Fig. 5 Examples of reconstructed images, when δϕ takes 1/4 of ΔϕFWHM |

|
| 图 6 dwm随着间隔Δϕ的变化 Fig. 6 This picture shows dwm varies with Δϕ |
在多个频率上测量弥漫射电辐射的偏振是研究银河系磁场的一种有效的方法。目前的法拉第旋率综合法是利用偏振强度与法拉第色散函数之间是傅里叶变换对,把观测到的偏振强度做傅里叶逆变换得到法拉第色散函数[1]。因受观测波段的限制,得出的解需要进行解卷积,所以需要一种更强有力的方法解决这一问题。
本文基于压缩感知的法拉第色散函数重构方法应用到实际观测频率范围中,并对可能影响该方法重构效果的因素分别进行了实验。实验结果表明,该方法的重构效果随着法拉第薄源的个数、源偏振强度的大小、相位以及两个法拉第薄源的法拉第深度之间间隔Δϕ的不同而出现较大差异,具有较大的随机性。大样本统计学实验发现,当ϕ空间的分辨率δϕ取ΔϕFWHM的1/3和1/4时,重构结果精确度最高,对其重构结果各峰值附近再次进行最小二乘拟合后得到的法拉第深度ϕ值更接近原始值。通过压缩感知法重构后的再次拟合,可以得到更为精确的法拉第深度ϕ值,因此该方法可以作为现有方法的一种补充,同时该方法对于重构得出的偏振强度普遍偏低,重构效果具有较大的随机性,所以,还需要不断地改进,提高其稳定性和精确度,以便更好地应用于实际观测数据中。
| [1] | BRENTJENS M A, DE BRUYN A G. Faraday rotation measure synthesis[J]. Astronomy & Astrophysics, 2005, 441(3): 1217–1228. |
| [2] | FRICK P, SOKOLOFF D, STEPANOV R, et al. Wavelet-based Faraday rotation measure synthesis[J]. Monthly Notices of the Royal Astronomical Society, 2010, 401(1): L24–L28. DOI: 10.1111/mnl.2010.401.issue-1 |
| [3] | FRICK P, SOKOLOFF D, STEPANOV R, et al. Faraday rotation measure synthesis for magnetic fields of galaxies[J]. Monthly Notices of the Royal Astronomical Society, 2011, 414(3): 2540–2549. DOI: 10.1111/mnr.2011.414.issue-3 |
| [4] | O'SULLIVAN S P, BROWN S, ROBISHAW T, et al. Complex Faraday depth structure of active galactic nuclei as revealed by broad-band radio polarimetry[J]. Monthly Notices of the Royal Astronomical Society, 2012, 421(4): 3300–3315. DOI: 10.1111/mnr.2012.421.issue-4 |
| [5] | CANDES E J, TAO T. Near-optimal signal recovery from random projections:universal encoding strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406–5425. DOI: 10.1109/TIT.2006.885507 |
| [6] | DONOHO D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. DOI: 10.1109/TIT.2006.871582 |
| [7] | LI F, BROWN S, CORNWELL T J, et al. The application of compressive sampling to radio astronomy. Ⅱ. Faraday rotation measure synthesis[J]. Astronomy & Astrophysics, 2011, 531: article id A126(8pp). |
| [8] | ANDRECUT M, STIL J M, TAYLOR A R. Sparse Faraday rotation measure synthesis[J]. The Astronomical Journal, 2012, 143(2): article id 33(12pp). |
| [9] | WILSON W E, FERRIS R H, AXTENS P, et al. The Australia Telescope Compact Array Broad-band Backend:description and first results[J]. Monthly Notices of the Royal Astronomical Society, 2011, 416(2): 832–856. DOI: 10.1111/j.1365-2966.2011.19054.x |
| [10] | SUN X H, RUDNICK L, AKAHORI T, et al. Comparison of algorithms for determination of rotation measure and Faraday structure. Ⅰ. 1100-1400 MHz[J]. The Astronomical Journal, 2015, 149(2): article id 60(13pp). |


