2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beining 100049, China
引力波探测不仅是检验广义相对论的重要途径,同时也为研究宇宙提供了一种全新的手段。继地基的LIGO和Virgo同时探测到由双中子星合并产生的引力波和伽马射线[1]以来,天基的引力波探测计划也在紧锣密鼓地进行中,其中之一的“天琴计划”是将3个星载激光干涉仪发射到绕地近圆轨道,然后通过观测卫星之间的距离变化探测引力波[2]。这3颗卫星组成等边三角形,臂长约为105 km,轨道平面指向由两颗快速绕转的白矮星组成的引力波辐射源RXJ0806.3 + 1527[3]。
“天琴计划”的第1步是实现激光测月和深空卫星激光测距,目前云南天文台已实现激光测月。为了满足“嫦娥4号”月球背面登陆器与地球的实时通讯,地月系L2点的晕轨道上需要放置一个中继星实现通讯中转[4]。目前,中继星“鹊桥”已于2018年6月14日成功入轨,为深空卫星激光测距提供了机会。文[5]针对地月L2点的中继星任务分析了发射窗口、地月转移时间、近月点高度、近月点倾角、轨道振幅等因素对地月L2点转移轨道和使命轨道特性的影响;文[6]针对中继星转移轨道的转移时间、近月点高度和晕轨道振幅等约束条件,研究了月球近旁L2点转移轨道的设计方法;文[7]研究了地月系L2点纯反射式激光测距技术和任务设计,并结合云南天文台1.2 m望远镜激光测距系统给出了预期系统能接收到的单脉冲回波光子数。由于中继星的星等(暗于17等,计算过程见附录)高于1.2 m望远镜光电探测的极限星等,所以有必要模拟一条晕轨道并对预报精度如何影响单脉冲回波光子数做出分析,进而评估中继星和月球处于不同位置关系时噪声对激光测距成功率的影响。本文根据轨道对称性理论和微分改正法[8]计算出一条地月系L2点的晕轨道,在此基础上估算了能量服从高斯分布的光斑在考虑大气抖动、望远镜抖动、中继星预报精度的情况下,单脉冲的回波光电子数和测距成功率随中继星横向轨道偏离的变化。
1 围绕L2点的晕轨道计算方法中继星在地月系中的圆形限制性三体问题(Circular Restricted Three Body Problem, CRTBP)指的是地球和月球绕地月系质心作圆周运动,中继星在地球和月球引力作用下的动力学问题,本文仅考虑中继星围绕L2点的周期运动。
定义地月距离d为基本的长度单位,地月周期P为基本的时间单位,那么无量纲的距离L*、时间t*、速度v*与有量纲的距离L、时间t、速度v之间的转换关系如下:
| $ \begin{array}{*{20}{c}} {{L^ * } = \frac{L}{d},}&{{t^ * } = 2{\rm{ \mathsf{ π} }}\frac{t}{P},}&{{v^ * } = \frac{{{L^ * }}}{{{t^ * }}} = v\frac{P}{{2{\rm{ \mathsf{ π} }}d}}.} \end{array} $ | (1) |
| $ P = 2{\rm{ \mathsf{ π} }}\sqrt {\frac{{{d^3}}}{{GM}}} , $ | (2) |
其中,G为引力常数;M为地球月球质量之和。圆形限制性三体问题在旋转坐标系下的无量纲运动方程[9]为
| $ \left[ {\begin{array}{*{20}{c}} {\dot x}\\ {\dot y}\\ {\dot z}\\ {{{\dot v}_x}}\\ {{{\dot v}_y}}\\ {{{\dot v}_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}}\\ {{v_z}}\\ {2{v_y} + \frac{{\partial U}}{{\partial x}}}\\ { - 2{v_x} + \frac{{\partial U}}{{\partial y}}}\\ {\frac{{\partial U}}{{\partial z}}} \end{array}} \right], $ | (3) |
其中,
| $ U\left( {x,y,z} \right) = \frac{1}{2}\left( {{x^2} + {y^2}} \right) + \frac{{1 - \mu }}{{{r_1}}} + \frac{\mu }{{{r_2}}}, $ | (4) |
| $ \begin{array}{l} {r_1} = \sqrt {{{\left( {x + \mu } \right)}^2} + {y^2} + {z^2}} ,\\ {r_2} = \sqrt {{{\left[ {x - \left( {1 - \mu } \right)} \right]}^2} + {y^2} + {z^2}} , \end{array} $ | (5) |
| $ \mu = \frac{{{m_2}}}{{{m_1} + {m_2}}}. $ | (6) |
其中,m1和m2分别为地球和月球的质量。圆形限制性三体问题存在一个Jacobian积分,即
| $ 2U\left( {x,y,z} \right) - \left( {v_x^2 + v_y^2 + v_z^2} \right) = C, $ | (7) |
其中,C为一个常数。若中继星的速度为0,那么(7)式化简为零速度曲面2U(x, y, z)=C;若令z=0,零速度曲面化简为零速度曲线2U(x, y)=C。
在t0时刻,取一个L2点附近的初始状态量(x0, 0, z0, 0, vy0, 0),经过半个周期τ后中继星的状态量可表示为
| $ \left[ \begin{array}{l} x\left( {{t_0} + \tau } \right)\\ y\left( {{t_0} + \tau } \right)\\ z\left( {{t_0} + \tau } \right)\\ {v_x}\left( {{t_0} + \tau } \right)\\ {v_y}\left( {{t_0} + \tau } \right)\\ {v_z}\left( {{t_0} + \tau } \right) \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{\phi _1}\left( {{x_0},0,{z_0},0,{v_{{y_0}}},0,\tau } \right)}\\ {{\phi _2}\left( {{x_0},0,{z_0},0,{v_{{y_0}}},0,\tau } \right)}\\ {{\phi _3}\left( {{x_0},0,{z_0},0,{v_{{y_0}}},0,\tau } \right)}\\ {{\phi _4}\left( {{x_0},0,{z_0},0,{v_{{y_0}}},0,\tau } \right)}\\ {{\phi _5}\left( {{x_0},0,{z_0},0,{v_{{y_0}}},0,\tau } \right)}\\ {{\phi _6}\left( {{x_0},0,{z_0},0,{v_{{y_0}}},0,\tau } \right)} \end{array}} \right], $ | (8) |
其中, ϕi(x0, 0, z0, 0, vy0, 0, τ)为一个流。从初始位置经过一个周期2τ后,位置偏量定义为
| $ \Delta r = \sqrt {{{\left[ {x\left( {{t_0} + 2\tau } \right) - {x_0}} \right]}^2} + {{\left[ {y\left( {{t_0} + 2\tau } \right) - {y_0}} \right]}^2} + {{\left[ {z\left( {{t_0} + 2\tau } \right) - {z_0}} \right]}^2}} . $ | (9) |
根据对称性原理[10],经过半个周期τ后中继星的状态量满足:
| $ \left[ {\begin{array}{*{20}{c}} {{\phi _2}\left( {{x_0},0,{z_0},0,{v_{{y_0}}},0,\tau } \right)}\\ {{\phi _4}\left( {{x_0},0,{z_0},0,{v_{{y_0}}},0,\tau } \right)}\\ {{\phi _6}\left( {{x_0},0,{z_0},0,{v_{{y_0}}},0,\tau } \right)} \end{array}} \right] = 0. $ | (10) |
固定x0,则(10)式含有3个未知数,采用微分改正法求z0,vy0,τ,(10)式化为
| $ {\left[ {\begin{array}{*{20}{c}} {{z_0}}\\ {{v_{{y_0}}}}\\ \tau \end{array}} \right]_{n + 1}} = {\left[ {\begin{array}{*{20}{c}} {{z_0}}\\ {{v_{{y_0}}}}\\ \tau \end{array}} \right]_n} - \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\phi _2}}}{{\partial {z_0}}}}&{\frac{{\partial {\phi _2}}}{{\partial {v_{{y_0}}}}}}&{\frac{{\partial {\phi _2}}}{{\partial \tau }}}\\ {\frac{{\partial {\phi _4}}}{{\partial {z_0}}}}&{\frac{{\partial {\phi _4}}}{{\partial {v_{{y_0}}}}}}&{\frac{{\partial {\phi _4}}}{{\partial \tau }}}\\ {\frac{{\partial {\phi _6}}}{{\partial {z_0}}}}&{\frac{{\partial {\phi _6}}}{{\partial {v_{{y_0}}}}}}&{\frac{{\partial {\phi _6}}}{{\partial \tau }}} \end{array}} \right]_{n\left| {{t_0} + \tau } \right.}^{ - 1}{\left[ {\begin{array}{*{20}{c}} {{\phi _2}}\\ {{\phi _4}}\\ {{\phi _6}} \end{array}} \right]_{n\left| {{t_0} + \tau } \right.}}, $ | (11) |
其中,
| $ \begin{array}{*{20}{c}} \begin{array}{l} \frac{{\partial {\phi _2}}}{{\partial {z_0}}} = \mathit{\Phi }\left( {2,3} \right),\\ \frac{{\partial {\phi _4}}}{{\partial {z_0}}} = \mathit{\Phi }\left( {4,3} \right),\\ \frac{{\partial {\phi _6}}}{{\partial {z_0}}} = \mathit{\Phi }\left( {6,3} \right), \end{array}&\begin{array}{l} \frac{{\partial {\phi _2}}}{{\partial {v_{{y_0}}}}} = \mathit{\Phi }\left( {2,5} \right),\\ \frac{{\partial {\phi _4}}}{{\partial {v_{{y_0}}}}} = \mathit{\Phi }\left( {4,5} \right),\\ \frac{{\partial {\phi _6}}}{{\partial {v_{{y_0}}}}} = \mathit{\Phi }\left( {6,5} \right), \end{array}&\begin{array}{l} \frac{{\partial {\phi _2}}}{{\partial \tau }} = {v_y},\\ \frac{{\partial {\phi _4}}}{{\partial \tau }} = 2{v_y} + \frac{{\partial U}}{{\partial x}},\\ \frac{{\partial {\phi _6}}}{{\partial \tau }} = \frac{{\partial U}}{{\partial z}}, \end{array} \end{array} $ | (12) |
其中,Φ为状态转移矩阵[11] (关于状态转移的定义和推导见附录)。当n为0时,[z0, vy0, τ]T 0为t0时刻的初始值,经过一次微分改正后,得到一个新的初始值[z0, vy0, τ]T 1,继续迭代(n足够大)会得到满足精度要求的初始值[z0, vy0, τ]nT。对于L1点用上述方法可以得到一条三维晕轨道,而对于L2点,用这种方法只能得到平面上的Lyapunov轨道,因为z0总是收敛到0。为了得到三维的晕轨道,需要用前面得到的平面Lyapunov轨道作为初始条件。固定z0,使x0, vy0,τ为变量,那么(10)式有3个未知数,采用微分改正法求x0,vy0,τ,(10)式化为
| $ {\left[ {\begin{array}{*{20}{c}} {{x_0}}\\ {{v_{{y_0}}}}\\ \tau \end{array}} \right]_{n + 1}} = {\left[ {\begin{array}{*{20}{c}} {{x_0}}\\ {{v_{{y_0}}}}\\ \tau \end{array}} \right]_n} - \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\phi _2}}}{{\partial {x_0}}}}&{\frac{{\partial {\phi _2}}}{{\partial {v_{{y_0}}}}}}&{\frac{{\partial {\phi _2}}}{{\partial \tau }}}\\ {\frac{{\partial {\phi _4}}}{{\partial {x_0}}}}&{\frac{{\partial {\phi _4}}}{{\partial {v_{{y_0}}}}}}&{\frac{{\partial {\phi _4}}}{{\partial \tau }}}\\ {\frac{{\partial {\phi _6}}}{{\partial {x_0}}}}&{\frac{{\partial {\phi _6}}}{{\partial {v_{{y_0}}}}}}&{\frac{{\partial {\phi _6}}}{{\partial \tau }}} \end{array}} \right]_{n\left| {{t_0} + \tau } \right.}^{ - 1}{\left[ {\begin{array}{*{20}{c}} {{\phi _2}}\\ {{\phi _4}}\\ {{\phi _6}} \end{array}} \right]_{n\left| {{t_0} + \tau } \right.}}, $ | (13) |
其中,
| $ \begin{array}{*{20}{c}} \begin{array}{l} \frac{{\partial {\phi _2}}}{{\partial {x_0}}} = \mathit{\Phi }\left( {2,1} \right),\\ \frac{{\partial {\phi _4}}}{{\partial {x_0}}} = \mathit{\Phi }\left( {4,1} \right),\\ \frac{{\partial {\phi _6}}}{{\partial {x_0}}} = \mathit{\Phi }\left( {6,1} \right), \end{array}&\begin{array}{l} \frac{{\partial {\phi _2}}}{{\partial {v_{{y_0}}}}} = \mathit{\Phi }\left( {2,5} \right),\\ \frac{{\partial {\phi _4}}}{{\partial {v_{{y_0}}}}} = \mathit{\Phi }\left( {4,5} \right),\\ \frac{{\partial {\phi _6}}}{{\partial {v_{{y_0}}}}} = \mathit{\Phi }\left( {6,5} \right), \end{array}&\begin{array}{l} \frac{{\partial {\phi _2}}}{{\partial \tau }} = {v_y},\\ \frac{{\partial {\phi _4}}}{{\partial \tau }} = 2{v_y} + \frac{{\partial U}}{{\partial x}},\\ \frac{{\partial {\phi _6}}}{{\partial \tau }} = \frac{{\partial U}}{{\partial z}}, \end{array} \end{array} $ | (14) |
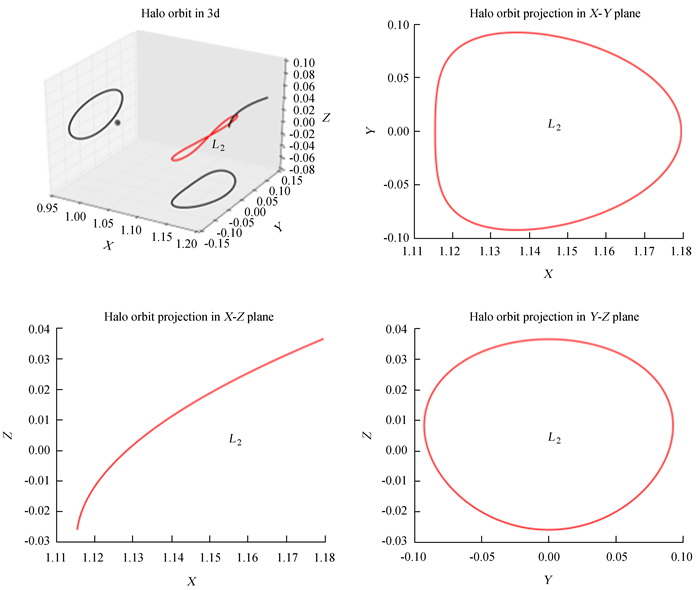
以L2为坐标原点,设定初始位置为(74 524.0, 0, -2 000.0) km,初始速度为(0, -2 763.0, 0) km/day,初始半周期为6.30天。通过(1)式和(2)式对初始状态量进行无量纲化后,积分运动方程和状态转移矩阵,求解微分改正方程(11),最后得到满足一个平面Lyapunov轨道的初始条件(1.181 714 308 650 075 9, 0, 3.593 303 527 781 356 3 × 10-22, 0, -0.161 707 122 057 949 57, 0)。该轨道周期为14.848 551 178 5天,位置偏量为1.578 016 320 24 × 10-11,Jacobian积分常数为3.150 560 441 73,状态转移矩阵的模为1.000 000 000 18 (接近于1),说明该轨道满足周期轨道条件。将平面Lyapunov轨道的初始条件做一个微小的改动,例如将z0改动到1.5 × 10-10,其他不变。积分运动方程和状态转移矩阵,求解微分改正方程(13),得到一个稍微远离平面的晕轨道。继续对z0做微小改动积分运动方程和状态转移矩阵,求解微分改正方程(13),不断重复。最后得到一条轨道周期为14.784 302 058 6天,初始条件为(1.179 549 767 505 286, 0, 0.036 621 093 75, 0, -0.163 192 959 324 161 45, 0)的晕轨道(见图 1和图 2)。该轨道的位置偏量为1.555 631 275 59 × 10-11,Jacobian积分常数为3.146 353 680 89,状态转移矩阵的模为0.999 999 999 964 (接近于1),说明满足周期轨道条件。
|
| 图 1 地月系L2点的晕轨道三维轨迹图及其在3个平面的投影。图中的尺度单位为地月距离,即384 402 km, 月球大小和晕轨道尺度为等比例画出,原点位于地月系质心 Fig. 1 Three-dimensional trajectory of Earth-Moon halo orbits around L2 and its projection on three orthogonal planes. The length scale is the distance between the Earth and the Moon, namely 384 402 km; the size of the Moon and halo orbit are plotted in equal proportion, and the origin is located at the mass center of the Earth-Moon system |
|
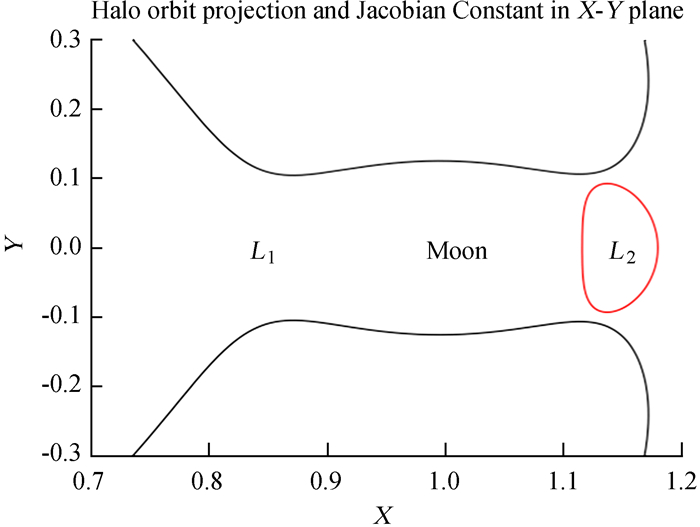
| 图 2 地月系L2点的晕轨道在X-Y平面的投影和零速度曲线 Fig. 2 Projection of the Earth-Moon halo orbit around L2 and its zero velocity curve in X-Y Plane |
从晕轨道在YZ平面的投影可知,晕轨道距离月球的最小角距离约为1.24 °,而月球的角半径约为0.26 °,因此满月时月球的光背景可能对中继星激光测距产生一定影响。从文[6]的计算可知,当晕轨道的振幅不小于4 000 km时即可实现月球无遮挡,本文中晕轨道的最小振幅为11 916 km,因此月球对该晕轨道没有遮挡。在确认满月对中继星激光测距的影响后,下面对中继星的测距成功率展开建模与分析。
2 测距成功率模型测距成功率指的是单光子探测器能够探测到至少一个光电子的概率。由于探测器探测光电子的概率服从泊松分布[12],即
| $ P\left( {k;\lambda } \right) = {e^{ - \lambda }}\frac{{{\lambda ^k}}}{{k!}}, $ | (15) |
测距成功率可以表示为
| $ \zeta = 1 - P\left( {0;N} \right) = 1 - {e^{ - N}}, $ | (16) |
其中,N为探测器产生的平均光电子数。光电子数越多信号越强,反之光电子数越少信号越弱。计算测距成功率的关键是计算探测器产生的平均光电子数,下文主要围绕如何计算探测器产生的平均光电子数展开讨论。
在不考虑望远镜抖动、大气抖动和中继星偏离预报轨道的理想情况下,望远镜发射的激光光斑中心理论上应该对准中继星,此时激光光斑的能量密度服从高斯分布(Gaussian Distribution),即
| $ \varepsilon \left( \rho \right) = \frac{{2{E_0}}}{{{\rm{ \mathsf{ π} }}\rho _{\rm{e}}^2}}\exp \left( { - \frac{{2{\rho ^2}}}{{\rho _{\rm{e}}^2}}} \right), $ | (17) |
其中,E0为光斑的总能量;ρ为光斑上任意一点到光斑中心的距离;ρe为光斑的特征半径并满足:
| $ \varepsilon \left( {{\rho _{\rm{e}}}} \right) = \frac{{\varepsilon \left( 0 \right)}}{{{{\rm{e}}^2}}}. $ | (18) |
取光斑的半径为1.5倍特征半径时,光斑内的能量占总能量的98.89%。光斑半径r与激光发散角θ、望远镜到中继星的距离R、望远镜有效口径D之间的关系为
| $ r = \frac{1}{2}\left( {R\theta + D} \right). $ | (19) |
当考虑望远镜抖动、大气抖动[13]以及中继星的轨道偏离时,光斑的平均能量密度分布可以表示为
| $ \bar \varepsilon = \int {\int_\Omega {\varepsilon * \left( {{g_{\rm{a}}} * {g_{\rm{t}}}} \right){g_{\rm{s}}}{\rm{d}}x{\rm{d}}y} } , $ | (20) |
其中,望远镜抖动gt(x, y)~
| $ \bar \varepsilon = \frac{{{E_0}}}{{2{\rm{ \mathsf{ π} }}\left( {\sigma _{\rm{t}}^2 + \sigma _{\rm{a}}^2 + \sigma _{\rm{s}}^2 + \frac{{\rho _{\rm{e}}^2}}{4}} \right)}}. $ | (21) |
大气抖动引起光斑中心漂移的均方差σa2表示为[15]
| $ \sigma _{\rm{a}}^2 = \frac{{10.22{R^2}}}{{{k^2}{r_0}^{\frac{5}{3}}{D^{\frac{1}{3}}}}}, $ | (22) |
其中,r0为大气相干长度;
| $ N = \bar \varepsilon {\eta _{\rm{e}}}T_{\rm{a}}^2T_{\rm{c}}^2S{\rho _{{\rm{reflection}}}}{\left( {{\mathit{\Omega }_{{\rm{reflection}}}}{R^2}} \right)^{ - 1}}{\rm{ \mathsf{ π} }}{\left( {\frac{D}{2}} \right)^2}{\eta _{\rm{r}}}{\eta _{\rm{q}}}\frac{\lambda }{{hc}}, $ | (23) |
其中,ηe 为望远镜发射系统的光学效率;Ta为大气透过率;Tc为卷云透过率①;S为中继星的有效反射面积;ρreflection为反射器的反射率;Ωreflection为反射立体角,ηr为望远镜接收系统的光学效率;ηq为探测器的量子效率;h为普朗克常数;c为真空中的光速。反射立体角Ωreflection与反射发散角θreflection的关系为
| $ {\mathit{\Omega }_{{\rm{reflection}}}} = 2{\rm{ \mathsf{ π} }}\left( {1 - \cos \frac{{{\theta _{{\rm{reflection}}}}}}{2}} \right). $ | (24) |
① Stephenson P C. Satellite laser ranging photon-budget calculations for a single satellite cornercube retroreflector: attitude control tolerance
3 结果与分析取激光脉冲的能量E0为3 000 mJ,测站到中继星的平均距离R取测站到L2点的距离,即442 548 km,望远镜的抖动标准差σt为0.1″ (乘以R换算成长度单位),大气的相干长度r0为10 cm,激光发射的发散角θ为2″,中继星的有效反射面积S为0.022 7 m2,反射器的反射率ρreflection为0.6,反射器的发散角θreflection为2″,大气透过率Ta为0.6,卷云透过率Tc为0.1,望远镜发射系统的光学效率ηe为0.4,接收系统的光学效率ηr为0.2,探测器的量子效率ηq为0.6,望远镜的有效口径D为1.06 m,激光的波长λ为532 nm[17]。通过前面计算的晕轨道可知,测站到中继星的最近距离和最远距离分别为427 287 km和451 889 km,保持其他参数不变,预报轨道横向标准差σs取0~5 km时探测器产生的光电子数和测距成功率见图 3。

|
| 图 3 光电子数(虚线)和测距成功率(实线)随预报轨道横向标准差的变化图,从上到下分别对应测站到中继星的平均距离、最远距离、最近距离的情况 Fig. 3 Variations of the photoelectron numbers (dotted line) and the laser ranging success probability (solid line) with the transverse standard deviation of the predicted orbit, From top to bottom, are corresponding to the average distance, the longest distance, and the closest distance from the station to the relay satellite |
从图 3可看出,光电子数和测距成功率随着中继星轨道横向标准差的增大而迅速减小,尤其是横向标准差位于1~2 km时下降最快,超过2 km后下降变缓。对于平均距离而言,当中继星没有偏离预报时,探测器产生的光电子数为0.151,成功率为14.07%,偏离2 km时,光电子数降为0.035,成功率降为3.46%,此时光电子数和成功率分别衰减了76.8%和75.4%;对于最近距离而言,当中继星没有偏离预报时,探测器产生的光电子数为0.174,成功率为16.01%,偏离2 km时,光电子数降为0.038,成功率降为3.77%,此时光电子数和成功率分别衰减了78.2%和76.4%;对于最远距离而言,当中继星没有偏离预报时,探测器产生的光电子数为0.139,成功率为13.02%,偏离2 km时,光电子数降为0.033,成功率降为3.29%,此时光电子数和成功率分别衰减了76.2%和74.7%。通过对比最近距离与最远距离的情况,探测器产生的光电子数从0.174降为0.139,成功率从16.01%降为13.02%。
4 结语本文针对位于地月系L2点的中继星“鹊桥”进行了晕轨道的模拟和计算,从数值上给出了一条轨道周期为14.78天,X方向的振幅为12 493 km,Y方向为34 596 km,Z方向为11 916 km的轨道。运行在该轨道上的中继星与月球的最小角距离约为1.24 °,而月球的角半径约为0.26 °,因此月球的光背景对中继星测距可能产生一定的影响。另一方面,由于轨道的最小振幅远大于月球遮挡的临界振幅4 000 km,所以月球对中继星不存在遮挡问题。中继星在V波段的视星等暗于17等,已经超出了1.2 m望远镜的极限星等,况且满月时望远镜受月光的影响,更增加了中继星可见的难度。在综合考虑大气抖动、望远镜抖动和中继星横向偏离预报轨道的情况下,建立了一个估算回波光电子数和测距成功率的模型。根据云南天文台的激光测距系统对中继星进行了回波光电子数和测距成功率分析,结果表明,光电子数和测距成功率随着中继星轨道横向标准差的增大而迅速减小,尤其是横向标准差位于1~2 km时下降最快,超过2 km后下降变缓。对于中继星到测站的平均距离而言,当中继星没有横向偏离时,探测器产生的光电子数为0.151,成功率为17.07%;横向偏离2 km时,光电子数降为0.035,成功率降为3.46%。对比最近距离与最远距离的情况,无横向偏移的情况下,探测器产生的光电子数从0.174降为0.139,成功率从16.01%降为13.02%。尽管最远距离与最近距离相差24 602 km,但探测器产生的光电子数没有明显的改变,这是由于轨道的振幅相对于整个地月距离而言较小的缘故。
附录 1 状态转移矩阵的定义和推导给定一个动力学系统
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {t,{t_0}} \right) = \frac{{\partial \mathit{\boldsymbol{X}}\left( t \right)}}{{\partial \mathit{\boldsymbol{X}}\left( {{t_0}} \right)}}, $ |
|
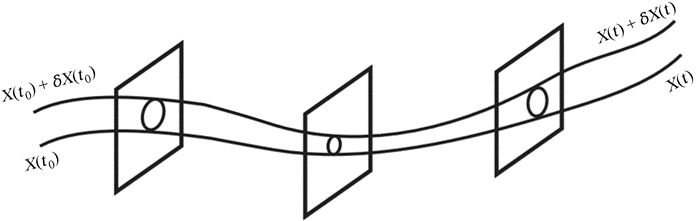
| 图 4 微小扰动随时间的演化示意图 Fig. 4 Schematic diagram of the evolution of small disturbances over time |
状态转移矩阵实际上是微分方程
由
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{X}}\left( t \right)}}{{{\rm{d}}t}} = \mathit{\boldsymbol{F}}\left[ {\mathit{\boldsymbol{X}}\left( t \right)} \right], $ |
可得
| $ \frac{{{\rm{d}}\left( {\mathit{\boldsymbol{X}}\left( t \right) + \delta \mathit{\boldsymbol{X}}\left( t \right)} \right)}}{{{\rm{d}}t}} = \mathit{\boldsymbol{F}}\left[ {\mathit{\boldsymbol{X}}\left( t \right) + \delta \mathit{\boldsymbol{X}}\left( t \right)} \right], $ |
一阶展开后,得到
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{X}}\left( t \right)}}{{{\rm{d}}t}} + \frac{{{\rm{d}}\left[ {\delta \mathit{\boldsymbol{X}}\left( t \right)} \right]}}{{{\rm{d}}t}} = \mathit{\boldsymbol{F}}\left[ {\mathit{\boldsymbol{X}}\left( t \right)} \right] + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \mathit{\boldsymbol{X}}}}\delta \mathit{\boldsymbol{X}}\left( t \right) + {\cal O}\left[ {\delta \mathit{\boldsymbol{X}}\left( t \right)} \right], $ |
略去高阶项得
| $ \frac{{{\rm{d}}\left[ {\delta \mathit{\boldsymbol{X}}\left( t \right)} \right]}}{{{\rm{d}}t}} = \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \mathit{\boldsymbol{X}}}}\delta \mathit{\boldsymbol{X}}\left( t \right). $ |
由于
| $ \delta \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {t,{t_0}} \right)\delta \mathit{\boldsymbol{X}}\left( {{t_0}} \right), $ |
将其代入上面的方程可得
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {t,{t_0}} \right)}}{{{\rm{d}}t}}\delta \mathit{\boldsymbol{X}}\left( {{t_0}} \right) = \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \mathit{\boldsymbol{X}}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {t,{t_0}} \right)\delta \mathit{\boldsymbol{X}}\left( {{t_0}} \right), $ |
最后化简得到
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {t,{t_0}} \right)}}{{{\rm{d}}t}} = \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \mathit{\boldsymbol{X}}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {t,{t_0}} \right). $ |
由定义可知t0时刻的状态转移矩阵Φ (t0, t0)= I,其中I为单位矩阵。对于周期轨道有Φ(t0 + 2τ, t0)= I,其中τ为半周期。
2 中继星V波段视星等的估算把太阳视为表面温度为5 778 K的黑体,那么单位面积、单位波长的太阳辐射功率满足普朗克辐射定律:
| $ {M_\lambda }\left( T \right) = \frac{{2{\rm{ \mathsf{ π} }}h{c^2}}}{{{\lambda ^5}\left( {{{\rm{e}}^{hc/\left( {\lambda kT} \right)}} - 1} \right)}}, $ |
其中,T为太阳表面温度;λ为波长;h为普朗克常数;c为光速。因为V波段的光谱范围为507~595 nm,中心波长为551 nm,因此在V波段对Mλ(T)积分可得到太阳表面单位面积的辐射功率:
| $ {F_{\rm{S}}} = \int_{\lambda 1}^{\lambda 2} {{M_\lambda }\left( T \right){\rm{d}}\lambda } , $ |
其中,λ1和λ2为V波段的下限波长和上限波长。中继星接收到的太阳辐射功率可表示为
| $ {F_{\rm{R}}} = {F_{\rm{S}}}{\left( {\frac{{{R_{\rm{S}}}}}{{{R_{\rm{E}}}}}} \right)^2}A, $ |
其中,RS为太阳的半径;RE为太阳到地月质心的距离;A为太阳帆的展开面积,此处取值为10 m2。由太阳帆反射到达测站单位面积上的太阳辐射功率为
| $ F = \rho \frac{{{F_{\rm{R}}}}}{{{\rm{ \mathsf{ π} }}{R^2}}}, $ |
其中,ρ为太阳帆的反射率,一般取值为
| $ {F_0} = \int_{{v_1}}^{{v_2}} {{F_{v,0}}{\rm{d}}v} = - \int_{{\lambda_1}}^{{\lambda_2}} {{F_{v,0}}\frac{c}{{{\lambda ^2}}}{\rm{d}}\lambda } , $ |
其中,v1和v2表示V波段的下限频率和上限频率;Fv, 0为单位面积单位频率的功率,取值为3 640 Jy。最后根据星等计算公式
| $ m = 2.5\log \left( {\frac{{{F_0}}}{F}} \right) $ |
求得中继星在V波段的视星等为17.2。
3 计算晕轨道的Python代码本文涉及的Python代码均可在smellysheep.com下载,主要包括:计算地月系5个平动点的位置,计算Jacobian积分常数,积分运动方程和状态转移矩阵,求解微分改正方程,寻求L2点的平面Lyapunov轨道和三维晕轨道。
| [1] | ABBOTT B P, ABBOT R, ABBOT T D, et al. GW170817:observation of gravitational waves from a binary neutron star inspiral[J]. Physical Review Letters, 2017, 119(16): 161101(16pp). |
| [2] | LUO J, CHEN L S, DUAN H Z, et al. TianQin:a space-borne gravitational wave detector[J]. Classical & Quantum Gravity, 2015, 33(3): 035010(32pp). |
| [3] | IRION R. Stellar pair whirls in a 5-minute dash[J]. Science, 2002, 295(5562): 1997. DOI: 10.1126/science.295.5562.1997 |
| [4] | 吴伟仁, 王琼, 唐玉华, 等. "嫦娥4号"月球背面软着陆任务设计[J]. 深空探测学报, 2017, 4(2): 111–117 |
| [5] | 高珊, 周文艳, 梁伟光, 等. 地月拉格朗日L2点中继星轨道分析与设计[J]. 深空探测学报, 2017, 4(2): 122–129 |
| [6] | 孙超, 唐玉华, 李翔宇, 等. 地-月L2点中继星月球近旁转移轨道设计[J]. 深空探测学报, 2017, 4(3): 264–269 |
| [7] | 何芸, 刘祺, 田伟, 等. 地月第二拉格朗日点卫星激光测距技术研究[J]. 深空探测学报, 2017, 4(2): 130–137 |
| [8] | HOWELL K C. Three-dimensional, periodic, 'halo' orbits[J]. Celestial Mechanics, 1984, 32(1): 53–71. |
| [9] | 孙义燧, 周济林. 现代天体力学导论[M]. 北京: 高等教育出版社, 2008. |
| [10] | PARKER J S, ANDERSON R L. Low-energy lunar trajectory design[M].[S. l.]: John Wiley & Sons, 2014. |
| [11] | TAPLEY B D, SCHUTZ B E, BORN G H. Statistical orbit determination[M].[S. l.]: Academic Press, 2004. |
| [12] | HENRIKSSON M. Detection probabilities for photon-counting avalanche photodiodes applied to a laser radar system[J]. Applied Optics, 2005, 44(24): 5140–5147. DOI: 10.1364/AO.44.005140 |
| [13] | 翟东升, 汤儒峰, 李春晓, 等. 实测中激光测距方程的完善[J]. 天文研究与技术, 2017, 14(1): 25–31 |
| [14] | BROMILEY P A. Products and Convolutions of Gaussian Probability Density functions[R]//Tina Memo. 2014. |
| [15] | YURA H T. Short-term average optical-beam spread in a turbulent medium[J]. Journal of the Optical Society of America, 1973, 63(5): 567–572. DOI: 10.1364/JOSA.63.000567 |
| [16] | 叶叔华, 黄珹. 天文地球动力学[M]. 济南: 山东科学技术出版社, 2000. |
| [17] | 李祝莲, 熊耀恒, 何妙婵, 等. 云南天文台人造卫星激光测距系统原理[J]. 天文研究与技术——国家天文台台刊, 2008, 5(3): 248–252 |


