全球卫星导航系统(Global Navigation Satellite System, GNSS)发展迅猛, 从前美国全球定位系统(Global Positioning System, GPS)一家独大的局面已被打破, 随着俄罗斯格洛纳斯(GLONASS)系统、欧洲伽俐略(Galileo)系统和中国北斗卫星导航系统(BeiDou Navigation Satellite System, BDS)先后崛起, 四大卫星导航系统并立共存的格局已基本形成。多系统组合导航已成为今后的主要发展趋势, 为用户提供更为精确可靠的定位、导航和授时服务[1-2]。现今, 即使是低成本的接收机都可以同时接收多个全球卫星导航系统的信号, 但是过多的冗余信息在增大定位解算计算量的同时增大功耗, 严重影响接收机定位的实时性[3]。因此, 选星步骤对于平衡接收机定位精度和计算复杂度, 起着至关重要的作用。
选星是选取最优的可见卫星组合的过程, 通常利用几何精度因子(Geometric Dilution of Precision, GDOP)作为结果优劣的判断标准, 其中的关键步骤是确定选星数目和设计选星方法[4]。多卫星导航系统选星算法是在原有的单系统选星算法的基础上发展起来的, 例如基于卫星几何构型的最大凸多面体体积法[5]和基于高度角和方位角的选星算法[4, 6]等。文[7]提出了一种适用于典型的城市障碍环境的选星算法, 通过单系统选星构成初始集合, 然后逐步扩大选星范围获得有最小几何精度因子值的选星结果。文[8]通过计算每颗卫星对几何精度因子的贡献, 然后剔除贡献最小的卫星达到选星目的。进化算法和机器学习也被大量运用到选星过程中, 包括粒子群算法[9]、模拟退火算法[10]、神经网络算法[11]、遗传算法[12-14]、支持向量机算法[15]等。其中, 文[9]认为由于神经网络算法需要大量的训练过程, 进化算法在处理选星问题时的速度更快。文[14]通过比较一系列选星方法, 结果表明基于支持向量机和遗传算法的选星性能更优。
上述的选星方法大多是在先验性的确定选星数目的条件下, 选择几何精度因子最优的可见卫星组合, 因此都是单目标优化方法。而在运用多系统导航的今天, 任意地点的平均可见导航卫星数目将超过40颗, 选多少颗星用于接收机的定位解算, 也成为了愈加重要的考量因素。在这方面, 以往的选星算法不能依据卫星几何布局的优劣, 机动地确定选星数目, 有着固有的局限性。当选星数目过少时, 几何精度因子值增加从而影响定位精度, 而选星数目过多时, 几何精度因子值减小, 但是大大增加接收机的计算负荷和功耗, 几何精度因子和选星数目是两个改善方向相互制约的目标, 其中一个目标的优化必然致使另一个目标的性能降低。因此, 选星问题可以转化为多目标优化问题求解。这样可以减少以往选星算法中, 先验性的确定选星数目所带来的主观影响, 同时不再拘泥于固定选星数带来的对几何精度因子极值的约束, 提高了选星的机动性。这种多目标选星方式, 能够得到几何精度因子和选星数目这两个目标权衡之后的最优选星方案, 可以更好地满足接收机定位解算的精度和实时性需求。
本文开创性地将多卫星导航系统选星问题作为有约束条件的多目标优化问题进行研究, 并给出了数学描述。进一步提出了一种基于非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ, NSGA-Ⅱ)的快速选星方法, 能同时优化几何精度因子和选星数目这两个目标, 并在各种全球卫星导航系统组合条件下进行仿真和分析, 结果验证了该方法解决多系统选星问题的有效性和实用性。
1 多目标选星问题的数学描述多目标选星问题是选择最优的卫星组合的过程, 目的是同时得到最小的选星数目和几何精度因子数值。为了能将选星问题转化为数学问题, 以便采用合适的算法求解, 同时降低选星求解的运算量, 本文根据选星问题的实际特性, 将数学模型表述为
| $ \left\{ \begin{array}{l} {\rm{Minimize}}\;\;\;{f_1}\left( x \right) = GDOP\left( {{x_1}, {x_2}, {x_3}, \ldots, {x_n}} \right)\\ {\rm{Minimize}}\;\;{f_2}\left( x \right) = \sum\limits_{j = 1}^n {{x_j}} \;\\ {\rm{Subject}}\;{\rm{to}}\;{g_1}\left( x \right) = k + 3-{f_2}\left( x \right) \le 0\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{g_2}\left( x \right) = {f_2}\left( x \right)-{m_{{\rm{max}}}} \le 0\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_j} = 0\;{\rm{or}}\;1, j = 1, 2, 3, \ldots, n. \end{array} \right.. $ | (1) |
决策向量X=(x1x2x3...xn)T代表不同的选星方案, 所在的空间为决策空间, n为可见导航卫星的总数。其中, xj代表第j颗可见卫星, xj=1表示卫星被选入, xj=0表示卫星未入选, 这样的设计可以方便地对选星方案进行二进制编码。两个目标函数f1(x)和f2(x)所在的空间为目标空间, 分别代表选星方案X的几何精度因子值和选星数目。gi(x)表示约束条件, 确定了解的可行域。对于k个卫星导航系统而言, 定位求解时需要k + 3颗可见卫星, 考虑到接收机自主完好性监测还有故障检测和排除的要求, 则需要选择更多的卫星。通常情况下, 定位时选用的卫星越多, 定位精度越高, 然而, 考虑到接收机的解算能力, 需要设置选星数目的上限mmax。因此, 选星问题可以作为有约束条件的多目标优化问题求解。
多系统定位需要考虑系统间的不一致性。在目前所能达到的测量精度水平下, 系统间坐标参考框架的偏差可以忽略不计, 所以需要重点考虑系统间的时间偏差。对于用户而言, 时间偏差可以并入接收机钟差, 每增加一个系统, 就增加一个钟差参数, 观测矩阵H也需要进行相应的扩展。因此, 多系统的几何精度因子和测量矩阵H可以表示为[15]
| $ GDOP = \sqrt {{\rm{trace}}[{{(H_n^T{H_n})}^{-1}}]}, $ | (2) |
| $ {H_n} = \left[{\begin{array}{*{20}{l}} {{H_A}}&{{1_A}}&{{0_A}}&{{0_A}}& \ldots \\ {{H_B}}&{{0_B}}&{{1_B}}&{{0_B}}& \ldots \\ {{H_C}}&{{0_C}}&{{0_C}}&{{1_C}}& \ldots \\ \ldots&\ldots&\ldots&\ldots&\ldots \end{array}} \right]. $ | (3) |
其中, 下标γ=A, B, C …表示不同的导航系统, 例如GPS、GLONASS、Galileo和BDS。用于定位解算的卫星数量n=nA+ nB + nC +…。在观测矩阵Hn中, Hγ是一个nγ × 3维的方向余弦矩阵, 1γ, 0γ分别为nγ维列向量, 用于解算系统钟差。
2 快速选星方法多目标优化旨在获得一组多目标函数折衷解的集合, 称为Pareto最优解集或者非支配解集, 然后通过一定的决策规则找到其中最满意的方案[16]。遗传算法(Genetic Algorithms, GA)作为一种模拟自然选择的启发式随机搜索算法, 被广泛运用于多目标优化领域。在现有的多目标遗传算法中, NSGA-Ⅱ算法求解多系统选星问题最为合适, 该算法运用了精英保留机制、快速非支配排序方法和计算拥挤距离的多样性保持策略[17]。NSGA-Ⅱ算法的基本思想为首先产生一个规模为N的初始种群; 然后在每一代的进化中, 父代种群Pt通过遗传的选择、交叉和变异3个基本操作, 得到子代种群Qt; 将父代种群和子代种群合并Pt∪Qt之后, 进行快速非支配排序, 再通过拥挤度计算确定个体虚拟的适应度; 最后选择最好的N个个体生成新的种群Pt+1; 依次循环, 直到满足结束条件。
由此可知, NSGA-Ⅱ算法的主要优点是快速非支配排序方法能降低计算的复杂度, 并且不用外部种群储存非支配个体, 因此初始种群的规模极大地影响算法的性能, 需要进行重点分析[18]。同时, NSGA-Ⅱ算法中使用的遗传算子, 包括模拟二进制交叉算子(Simulated Binary Crossover)和多项式变异算子(Polynomial Mutation), 并不适用于二进制编码的选星问题, 因而需要设计更为合适的遗传算子。此外, 获得Pareto最优解集只是解决多目标优化问题的第1步, 之后同样重要的步骤是通过一定的决策规则从Pareto最优解集中选择一个满意解。因此, 依据NSGA-Ⅱ算法的上述特性, 本文提出了一种改进的基于NSGA-Ⅱ算法的多目标选星方法, 整体思路沿用NSGA-Ⅱ算法, 但是在生成初始种群时, 利用了选星问题的序贯性, 改进了处理约束方法, 同时选取合适的遗传算子, 并设计最后决策时使用的效用函数。
2.1 初始化种群多目标选星问题可以方便地采用二进制编码方式。假设某时刻的可见卫星总数为n, 按照顺序编排之后, 将每颗卫星都设为一个基因, 入选时记为1, 未入选时记为0。编码后的所有可见卫星组成一个长度为n的二进制字符串, 称为一条染色体。每条染色体代表一个可能的选星方案。通常情况下, 初始种群由一组随机生成的染色体组成。
连续选星问题可以看作是一个序贯决策(Sequential Decision-Making)过程, 需要在动态环境下, 序贯性地在每个时刻, 根据所处的状态和以前的记录, 从一组可行方案中做出最优决策。文[19]进行过详尽的分析, 证实了每一个时刻的最优选星组合同样也是一定时间间隔范围内的最优选星组合, 当时间间隔设置为1 min时, 95%的时间内可以满足这个规律。图 1对比展示了一个全球定位系统和北斗导航系统组合在相邻的前后两个时刻的最优选星方案, 仰角门限为5 °, 选星数目为7。由图 1可知, 在这个时间跨度内, 最优选星方案中有5颗可见卫星依然匹配, 有2颗发生了变化。发生变化是因为随着时间的推移, 有卫星出现或者消失在视野范围内, 这种情况也仅仅发生在5%的时间内。结果证明, 可以利用上一时刻的选星结果生成下一时刻的选星方案。
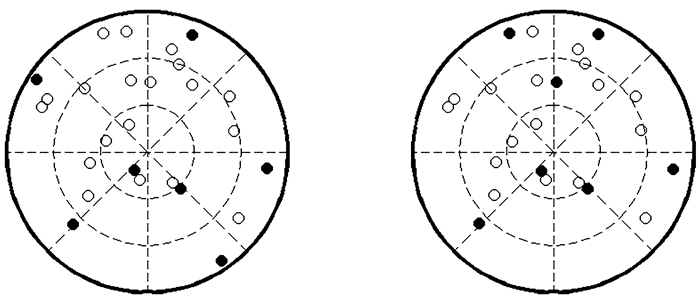
|
| 图 1 全球定位系统和北斗导航系统前后两个时刻的最优选星方案对比 Figure 1 Comparison of the GPS/BDS optimal satellite subsetsat two time points |
基于选星问题的序贯性, 前一时刻的Pareto最优解集和下一时刻的最优解集, 应该相同或者具有极大的相似性。因此可以将前一时刻的Pareto最优解集译码后, 获得最优的选星结果, 然后去掉其中下一时刻不可见的卫星, 生成新的种群, 作为下一时刻的初始种群P0。这样就可以利用前一刻的Pareto最优解集, 生成下一时刻的初始种群, 具体过程如图 2。
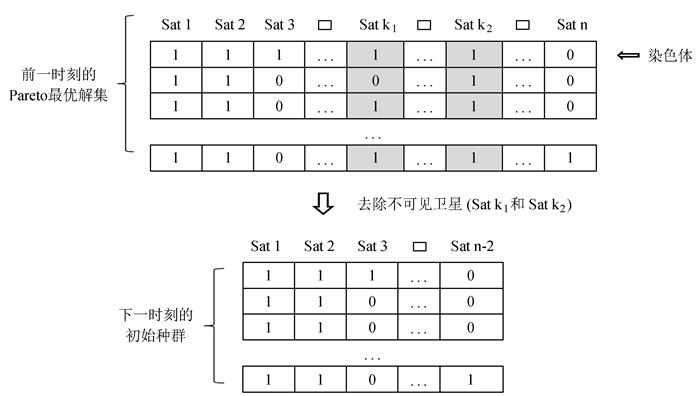
|
| 图 2 二进制编码和基于序贯性生成初始种群 Figure 2 Binary encoding and Population initialization with sequential decision method |
基于上述设置, 初始种群已经接近最优解集, 于是利用较小的种群规模, 经过较少的进化代数, 就可以得到满意的选星结果。这将大大减小计算的复杂度, 并且能提高连续选星的效率, 这样的改进方式也可以广泛运用于其他的选星方法中。
2.2 约束处理有约束条件的多目标优化算法的收敛性和分布性的优劣, 取决于约束处理技术和多样性维护策略, 现有的约束处理技术包括惩罚函数法、随机排序法、可行性准则法和混合算法等[20]。其中惩罚函数法需要设置合适的惩罚系数, 不然就会早熟或者停滞。随机排序法稳定性较差, 而基于解之间的约束支配关系, 可行性准则认为[21]:(1)可行解支配不可行解; (2)可行解之间适应度高的解支配适应度低的解; (3)不可行解之间约束违反度小的解支配约束违反度大的解。该算法由于过分强调了可行解优于不可行解, 容易陷入局部最优。
而选星问题的最优解往往存在于约束边界, 为了保持解的多样性, 约束违反度较小的不可行解也需要在种群中得到一定的保留。为此, 本文提出了一个保持一定比例不可行解的新的选择算子ρ, 代表种群中不可行解所占比例的阈值, ρ是个单调递减函数, 其表达式为
| $ \rho = \left\{ \begin{array}{l} b\left( {a-\frac{t}{{{G_{{\rm{max}}}}}}} \right), \frac{t}{{{G_{{\rm{max}}}}}} \le a\\ \;\;\;\;\;\;\;\;\;0, {\rm{otherwise}} \end{array} \right., $ | (4) |
其中, t为进化代数; Gmax为最大进化代数; a和b均为[0, 1]范围内的可调参数, 在选星问题中可以设置为a=0.5, b=0.2。在设定上述阈值的基础上, 生成新种群Pt+1的选择操作如下:
(1) 合并规模为N的父代和子代种群, 生成规模为2N的Rt=Pt∪Qt; 设置新种群Pt+1=∅, i=1。
(2) 如果Rt中不可行解的个数Ninfeasible<int(ρN), 选择所有的不可行解xinfeasible; 如果Ninfeasible≥int(ρN), 则利用公式
(3) 对Rt中的可行解进行快速非支配排序, 并标记非支配等级Fi, i=1, 2, 3…当Pt+1 + Fi < N时, 按照非支配等级高低依次选择个体Pt+1=Pt+1∪Fi, i=i + 1;然后依据拥挤度排序, 在非支配等级Fi中选择分布性较好的可行解填充, Pt+1= Pt+1∪Fi[1:N-Pt+1]。
改进的约束处理方式通过保留一定数量的不可行解, 增强了在可行域边缘的搜索能力, 一定程度上维护了种群的多样性, 避免了早熟现象的发生。
2.3 遗传算子遗传算子包括选择算子、交叉算子和变异算子。变异操作指以一定的概率改变个体编码串中的某个或者某些基因位置的过程。对于选星问题可以采用基本位变异方法, 依据变异概率指定变异点, 然后对指定的变异点上的基因值做取反运算即可。交叉算子的选用一般与编码方式有关, 二进制编码常用的交叉操作主要有单点交叉、多点交叉、均匀交叉、循环交叉和部分匹配交叉等。为了有效保留优秀的基因, 本文选用异或交叉算子, 采用轮盘法则, 随机选择父代进行交叉操作, 操作方式如图 3。

|
| 图 3 异或交叉算子 Figure 3 XOR crossover |
多目标进化算法通常分为优化和决策两个步骤, 所采用的技术一般分为3类:先验决策方法(决策→优化)、后验决策方法(优化→决策)和交互决策方法(优化←→决策) [22]。本文采用后验决策方法, 在利用改进的NSGA-Ⅱ算法获得选星问题的Pareto最优解集之后, 用一个更高层次的效用函数选择一个偏好解。针对双目标优化的选星问题, 设计的效用函数表示为
| $ \begin{array}{l} U\left( {{x_j}} \right) = {w_1} \times \frac{{{f_1}\left( {{x_j}} \right)-{f_1}^{{\rm{min}}}}}{{{f_1}^{{\rm{max}}}-{f_1}^{{\rm{min}}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{w_2} \times \frac{{{f_2}\left( {{x_j}} \right)-{f_2}^{{\rm{min}}}}}{{{f_2}^{{\rm{max}}}-{f_2}^{{\rm{min}}}}}, \end{array} $ | (5) |
其中, xj为Pareto最优解集中第j个选星方案; 两个目标函数fi(x)的最大值和最小值分别为fimax和fimin; w1和w2为设计的权值。利用效用函数计算得到Pareto最优解集中每个选星方案的适应值后, 适应值最小的选星方案最优, 即为选星结果。经过解码后, 可利用选星结果进行定位解算。
这种后验决策方法能够有效地控制决策者的喜好带来的主观影响, 并且能够很好地利用遗传算法的特性, 并行处理各个目标, 在具备全局最优搜索性的条件下, 快速高效地优中选优, 最终得到满意的选星结果。
根据上述分析和改进方案, 基于NSGA-Ⅱ算法的多目标快速选星方法的流程图如图 4。
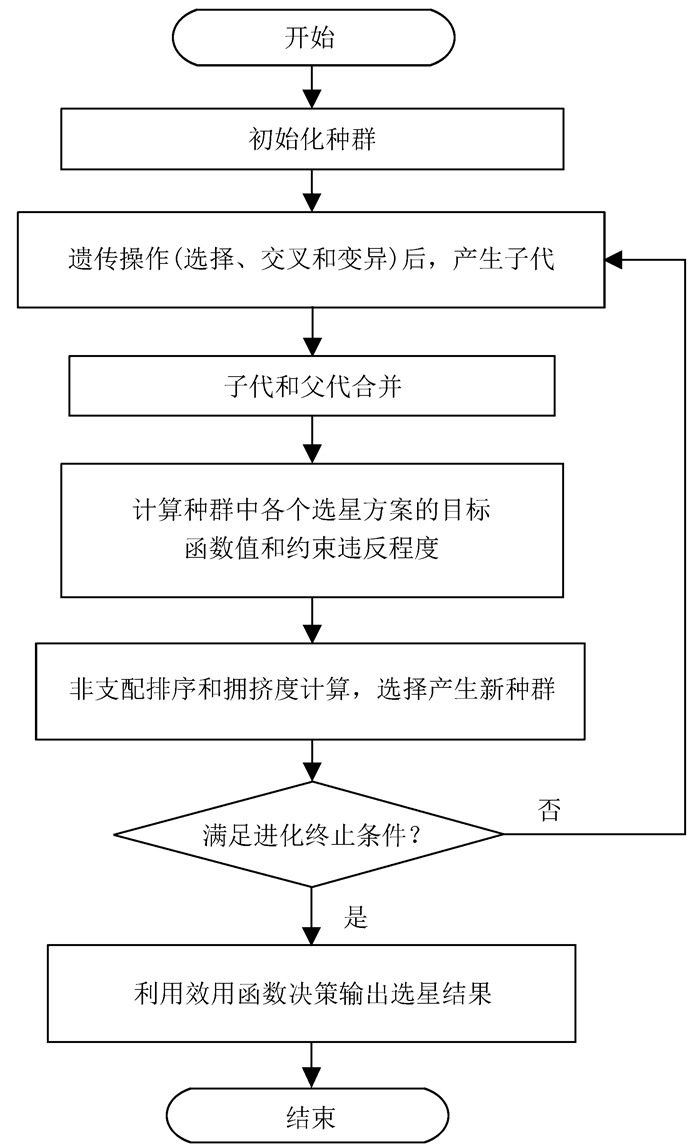
|
| 图 4 基于NSGA-Ⅱ算法的多目标快速选星方法的流程图 Figure 4 Flow chart of fast satellite selection method based on NSGA-Ⅱ |
为了测试基于NSGA-Ⅱ算法的多目标快速选星方法的性能, 本文用自编软件进行了仿真分析。仿真环境为各个卫星导航系统全面运行时的情况。其中, 全球定位系统和GLONASS由于已经部署完成, 于是根据实际情况, 采用了真实的星历。对于中国北斗系统按照35颗卫星进行仿真, 其中包括5颗地球同步轨道卫星、3颗倾斜地球同步轨道卫星和27颗中地球轨道卫星。依据普遍性, 采用了两种组合方案:GPS + BDS和GPS + BDS + GLO。
图 5为某时刻GPS + BDS组合系统在选星前, 全球范围内的可见卫星数和几何精度因子, 分辨率为5 ° × 5 °, 高度截止角设为5 °。图 6是该时刻的选星数目和选星后的几何精度因子, 设选星数目的最大值mmax=15。选星前后的具体结果见表 1。由此可知, 在该时刻全球的平均可见卫星数约为23颗, 如果从中选取7颗, 将有C237=245 157种组合方式, 而可用的卫星数目更多时, 选星的组合方式将成几何级数增长, 这对于遍历法将是沉重的计算负荷, 几乎不能实现。而经过本文提出的选星过程, 选择的卫星数目均值为10.595 3, 为选星前的46.7%, 使用的卫星数目减少, 定位解算时运算量可以减少60%, 接收解算的效率得到显著提高。

|
| 图 5 GPS + BDS选星前可见卫星数目和几何精度因子 Figure 5 (a) The number of visible satellites of GPS + BDS and (b) GDOP prior to the selection process |

|
| 图 6 GPS + BDS选星数目和选星后的几何精度因子 Figure 6 (a) The number of selected satellites of GPS + BDS and (b) GDOP following the selection process |
| 选星数目/颗 | 几何精度因子 | ||||||
| 最小值 | 最大值 | 均值 | 最小值 | 最大值 | 均值 | ||
| 选星前 | 15 | 32 | 22.702 7 | 0.965 2 | 1.950 3 | 1.316 8 | |
| 选星后 | 6 | 15 | 10.595 3 | 1.241 1 | 2.166 2 | 1.568 2 | |
在选星前几何精度因子的最小值为0.965 2, 当几何精度因子大于1时, 是定位误差放大因子, 当几何精度因子小于1时, 说明卫星的几何布局较好, 于是具有了定位误差缩小的功能。在选星后的几何精度因子最大值不超过3, 依然可用性良好, 而且选星后的几何精度因子均值为1.568 2, 仅比选星前的均值增大了0.2左右, 说明选星方法能够很好地保持接收机的定位精度。
在GPS + BDS + GLO系统组合导航的情况下, 分别对选星问题进行仿真, 使用Intel Core i7-5500U (2.4 GHz/L3 4 M)处理器。可以代表仿真时间为24 h, 采样间隔为60 s, 用户位于P点(39.9 °N, 116.3 °E, 0), 选星数目的最大值mmax设为该时刻可见卫星数目的60%。高度角的设置主要是为了控制接收机接收卫星的数目, 通常情况下, 由于树木或者高楼的遮挡, 以及多路径效应影响, 高度角小的卫星信号受到的干扰比较大, 定位解算的结果不准确, 所以接收机需要尽量不使用高度角小的卫星。在实际测量中, 需要根据周围环境的开阔程度调整高度截止角的设置, 环境越开阔, 高度截止角可以设置的越小。所以在本文的仿真实验中, 高度截止角分别设置为5 °、15 °和30 °, 结果见表 2及图 7。
| 高度截止角 | 选星数目/颗 | 几何精度因子 | ||||||
| 最小值 | 最大值 | 均值 | 最小值 | 最大值 | 均值 | |||
| 5° | 选星前 | 30 | 38 | 33.383 1 | 0.981 3 | 1.583 3 | 1.206 4 | |
| 选星后 | 7 | 21 | 13.551 7 | 1.133 7 | 1.684 3 | 1.460 3 | ||
| 15° | 选星前 | 24 | 31 | 27.652 3 | 1.330 8 | 2.084 7 | 1.646 9 | |
| 选星后 | 7 | 18 | 11.510 8 | 1.564 5 | 2.380 5 | 1.848 6 | ||
| 30° | 选星前 | 15 | 22 | 18.732 1 | 2.330 8 | 4.958 5 | 3.220 9 | |
| 选星后 | 6 | 12 | 9.190 8 | 2.528 4 | 4.880 7 | 3.348 4 | ||
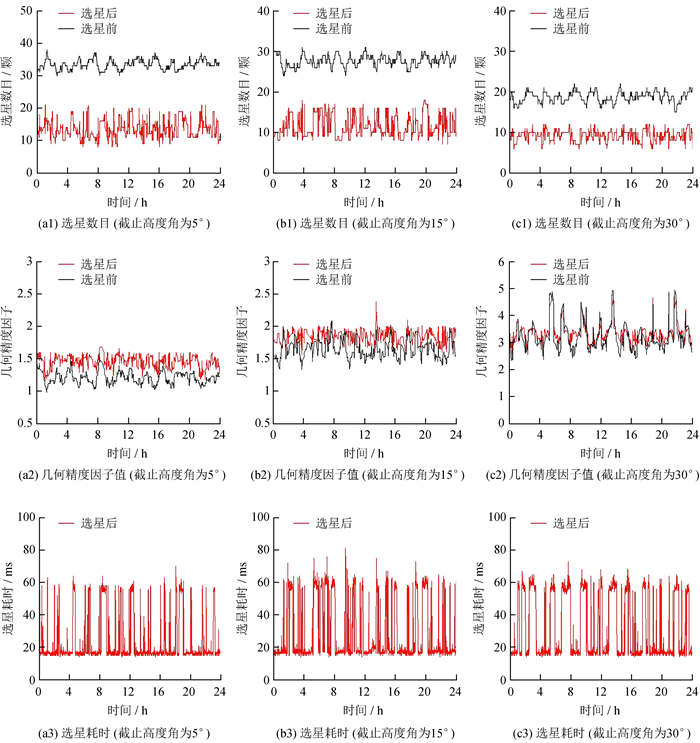
|
| 图 7 GPS + BDS + GLO不同截止高度角的选星结果比较 Figure 7 Comparison of GPS + BDS + GLO satellite selection results at elevation mask angles 5 °, 15 °and 30 °. (a1-3) number of satellites selected; (b1-3) GDOP values; (c1-3) computing time |
当高度截止角为5 °时, 选星数目均值为选星前卫星数目的40%, 选星后几何精度因子的最大值小于1.7, 与选星前的最大值相当, 同时选星后的几何精度因子的平均值相比于选星前只增加了0.26。选星后的几何精度因子在仿真时段内与选星前差别不大, 保持了良好的可用性。当高度截止角为15 °时, 有一部分时间段内, 选星后的几何精度因子值比选星前的还要小, 这说明在定位解算的时候确实有许多冗余信息, 需要经过选星过程剔除, 同时说明本文设计的选星方法性能优良, 能有效地寻找合适的选星方案。这种优越性在高度截止角为30 °时表现更为突出, 在30%的时间段内, 选星后的几何精度因子优于选星前, 这也说明了选星的必要性。由图 7可知选星耗时分布在10 ms至70 ms之间, 均值约为30 ms, 证明了算法的实时性。
由于本文提出的选星方法为全局搜索算法, 不依赖于卫星之间的几何分布, 所以没有适用条件的限制, 特别适用于有遮挡或者障碍的复杂情况。同时, 可以调整算法中的主要参数和关键步骤, 例如种群规模、进化代数、约束处理方法、效用函数和终止条件等, 提高选星算法的性能, 满足用户定位的精度或者实时性需求。
4 结论随着全球卫星导航系统的飞速发展, 可见的导航卫星数目日益增多, 接收机的性能日益增强, 选星数目也成为选星问题中重要的考量因素。本文将多系统选星问题作为有约束条件的多目标优化问题进行研究, 并给出了多目标选星问题的数学描述。这种多目标选星方式可以同时优化几何精度因子和选星数目这两个目标, 这样可以同时满足接收机定位解算的精度和实时性需求, 与传统固定数目的选星方法相比, 减小了先验性需求, 具有更好的灵活性和机动性。
在此基础上, 本文提出了基于NSGA-Ⅱ算法的多目标选星方法。利用选星问题的序贯性, 使用上一时刻的选星结果生成下一时刻的初始解集, 大大减少计算的复杂度, 提高了选星的效率, 这样的改进方式也可以运用于其他的选星方法中。同时改进了约束处理方式, 通过保留一定的不可行解保持种群的多样性, 防止局部收敛, 提高了算法的边缘搜索能力。进一步结合选星问题的特征, 选择了合适的遗传算子和用来决策的效用函数, 保证了算法的可用性。通过仿真证实了方法的实时性和有效性, 能够在降低接收机负担的同时获得良好的定位精度, 而且选星过程不依赖卫星的几何位置分布, 特别适用于有障碍或者遮挡的复杂情况。
| [1] | Li X X, Zhang X H, Ren X D, et al. Precise positioning with current multi-constellation global navigation satellite systems:GPS, GLONASS, Galileo and BeiDou[J]. Scientific Reports, 2015, 5: 1–14. DOI: 10.9734/JSRR |
| [2] | 谢钢. 全球导航卫星系统原理—GPS、格洛纳斯和伽利略系统[M]. 北京: 电子工业出版社, 2013. |
| [3] | Pesyna Jr K M, Heath Jr R W, Humphreys T E. Precision limits of low-energy GNSS receivers[C]//Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation. 2013. |
| [4] | Zhang M, Zhang J. A fast satellite selection algorithm:beyond four satellites[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(5): 740–747. DOI: 10.1109/JSTSP.2009.2028381 |
| [5] | Blanco-Delgado N, Nunes F D. Satellite selection method for multi-constellation GNSS using convex geometry[J]. IEEE Transactions on Vehicular Technology, 2010, 59(9): 4289–4297. DOI: 10.1109/TVT.2010.2072939 |
| [6] | Meng F, Wang S, Zhu B. Research of fast satellite selection algorithm for multi-constellation[J]. Chinese Journal of Electronics, 2016, 25(6): 1172–1178. DOI: 10.1049/cje.2016.10.009 |
| [7] | Peng A, Ou G, Li G M. Fast satellite selection method for multi-constellation Global Navigation Satellite System under obstacle environments[J]. IET Radar, Sonar & Navigation, 2014, 8(9): 1051–1058. |
| [8] | Li G Y, Xu C D, Zhang P F, et al. A modified satellite selection algorithm based on satellite contribution for GDOP in GNSS[M]. Berlin: Springer-Verlag, 2012: 415-421. |
| [9] | Mosavi M R, Shiroie M. Efficient evolutionary algorithms for GPS satellites classification[J]. Arabian Journal for Science and Engineering, 2012: 1–13. |
| [10] | Ranjbar M, Mosavi M R. Simulated annealing clustering for optimum GPS satellite selection[J]. International Journal of Computer Science Issues, 2012, 9: 100–104. |
| [11] | Azami H, Sanei S. GPS GDOP classification via improved neural network trainings and principal component analysis[J]. International Journal of Electronics, 2014, 101(9): 1300–1313. DOI: 10.1080/00207217.2013.832390 |
| [12] |
霍航宇, 张晓林. 组合卫星导航系统的快速选星方法[J]. 北京航空航天大学学报, 2015, 41(2): 273–282 Huo Hangyu, Zhang Xiaolin. Fast satellite selection method for integrated navigation systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 273–282. |
| [13] |
宋丹, 许承东, 胡春生, 等. 基于遗传算法的多星座选星方法[J]. 宇航学报, 2015, 36(3): 300–308 Song Dan, Xu Chengdong, Hu Chunshang, et al. Satellite selection with genetic algorithm under multi-constellation[J]. Journal of Astronautics, 2015, 36(3): 300–308. |
| [14] | Wu C H, Su W H, Ho Y W. A study on GPS GDOP approximation using support-vector machines[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(1): 137–145. DOI: 10.1109/TIM.2010.2049228 |
| [15] | Teng Y, Wang J. New characteristics of geometric dilution of precision (GDOP) for multi-GNSS constellations[J]. Journal of Navigation, 2014, 67(6): 1018–1028. DOI: 10.1017/S037346331400040X |
| [16] | Deb K, Sindhya K, Hakanen J. Multi-objective optimization[M]. Boca Raton: CRC Press, 2016: 145-184. |
| [17] | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197. DOI: 10.1109/4235.996017 |
| [18] | Konak A, Coit D W, Smith A E. Multi-objective optimization using genetic algorithms:a tutorial[J]. Reliability Engineering & System Safety, 2006, 91(9): 992–1007. |
| [19] | Swaszek P F, Hartnett R J, Seals K C, et al. A temporal algorithm for satellite subset selection in multi-constellation GNSS[C]//Proceedings of the 2017 International Technical Meeting of the Institute of Navigation. 2017: 1147-1159. |
| [20] | Coello Coello C A. Constraint-handling techniques used with evolutionary algorithms[C]//Proceedings of the 2016 on Genetic and Evolutionary Computation Conference Companion. 2016: 563-587. |
| [21] | Deb K. An efficient constraint handling method for genetic algorithms[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 186(2): 311–338. |
| [22] | Tan K C. Advances in evolutionary multi-objective optimization[M]. Berlin: Springer-Verlag, 2013: 7-8. |



