2. 中国科学院国家天文台, 北京 100012
2. National Astronomical Observatories, Chinese Academy of Science, Beijing 100012, China
国际GNSS服务中心(International GNSS Service, IGS)提供的精密星历通常用于全球定位系统精密单点定位等数据处理中,但国际GNSS服务中心发布的精密星历采样间隔是15 min,而在全球定位系统精密定位中接收机的采样率一般远小于这个值,因此,需要对精密星历进行高精度的插值。另一方面,由于国际GNSS服务中心精密星历仅提供当天00:00:00~23:45:00时间段的星历数据,若想仅用当天的数据得到23:45:00~24:00:00时间段的星历数据,还需要进行外推以获得任意时刻的卫星坐标。
要使插值定位结果平滑、稳定,要求插值多项式及其导数连续平滑,较为常见的插值方法有切比雪夫多项式插值法、牛顿多项式插值法和拉格朗日插值法等[1-3]。在目前的数据处理中,拉格朗日插值应用较广,文[4]指出拉格朗日插值法在本质上与内维尔插值法相同;文[5]将拉格朗日插值法改进,利用滑动式拉格朗日插值法获得全球定位系统精密星历;文[6]对比了拉格朗日和牛顿插值法的内插效果,对插值结果进行了总结分析。上述研究中,多种插值方法在一定时段内需要进行高低阶组合才能达到最优效果,且外推效果普遍不很理想。由于广义延拓逼近法构造的插值函数在所有同阶插值函数中具有最小平方逼近误差,为此,本文基于广义延拓原理对全球定位系统精密星历进行插值外推,利用求得的逼近函数解算任意时刻的全球定位系统卫星的精密坐标。
1 广义延拓内插及外推模型广义延拓逼近法在分片边界点上满足插值条件,使分片间变化协调,并充分利用分片插值区域的周围结点信息,实现分片区域内部的最佳拟合,结合插值法和拟合法的优点,在数据处理时实现了高精度的逼近[7-9]。
首先在整域内进行剖分处理,以便在单元域内寻找逼近函数及基函数,将定义域W剖分成n个互不重叠的子域Wi(i=1, 2, ..., n):
| $ W = \bigcup\nolimits_{i = 1}^n {{W_i}} , $ | (1) |
单元域Wi有r个结点,对应结点坐标为xe(e=1, 2, ..., r),结点坐标xe(e=1, 2, ..., r)满足定义域xe-1 < xi < xe。现将单元域Wi延拓至W′i,W′i成为延拓域,结点坐标xe(e=1, 2, ..., r),满足延拓域为x′e-1 < xi < x′e,如图 1。
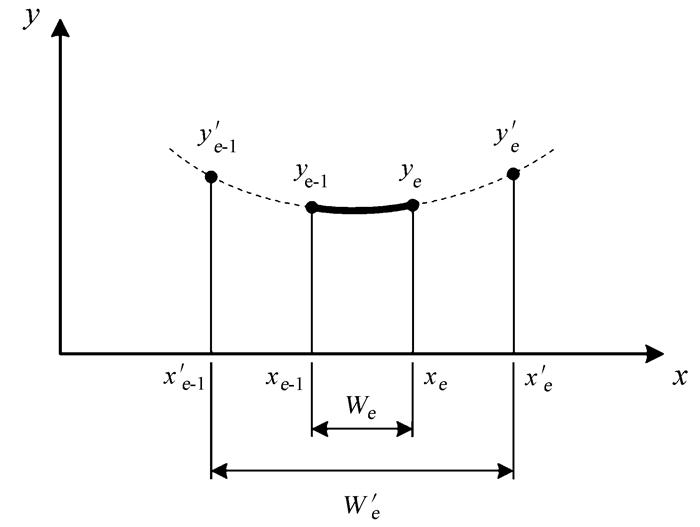
|
| 图 1 延拓域及相应函数值 Figure 1 Extension domains and their correspondingfunction values |
设延拓域W′i内有s个结点(s > r),利用含有较多结点的延拓域构造单元域内逼近函数ye(x):
| $ {y^e}\left( x \right) = \sum\limits_{j = 1}^v {{a_j}{g_j}\left( x \right)} ,\;\;\;\;x \in \left[ {{x_{e - 1}},{x_e}} \right], $ | (2) |
其中,gj(x)(j=1, 2, ..., v)为Wi上的一组基函数;aj(j=1, 2, ..., v)为待定系数;v为逼近函数项数,且r < v < s。在求解函数的待定系数时,将x的适用范围由单元域Wi扩大至延拓域W′i。则在延拓域建立如(3)式的广义延拓逼近内插模型,(xi, yi)为先验信息采样点,I(a1, a2, ..., aj)为逼近函数与先验值的误差:
| $ \left\{ {\begin{array}{*{20}{c}} {\min I\left( {{a_1},{a_2}, \cdots ,{a_j}} \right) = \min \sum\limits_{i = 0}^s {{{\left[ {{a_j}{g_j}\left( {{x_i}} \right) - {y_i}} \right]}^2}} }\\ {s.t.\left\{ {\begin{array}{*{20}{c}} {{a_j}{g_j}\left( {{x_{e - 1}}} \right) = {y_{e - 1}}}\\ {{a_j}{g_j}\left( {{x_e}} \right) = {y_e}} \end{array}} \right.} \end{array}} \right.. $ | (3) |
广义延拓逼近法将单元域嵌套在延拓域中,吸收单元域外延拓域中的结点信息构造单元域内的拟合逼近函数,同时约束单元域边界结点,实现相邻单元逼近函数的协调和连续,从而达到单元域内逼近函数的最佳拟合效果。利用广义延拓构造的逼近函数即可对目标变量进行插值处理。
广义延拓插值模型不但可以用作内插模型,也可以作为外推模型用于外延应用的场合。对一组不断增长的数据序列(x1, t1), (x2, t2), ..., (xi, ti), ..., (xn, tn),i=1, 2, ..., n,已知tn以前的数据值,根据先验数据的变化规律和趋势,欲求tn+1时刻的xn+1值,数据外推示意图如图 2。

|
| 图 2 数据外推示意图 Figure 2 Data extrapolation intent |
按照广义延拓插值外推的设计理念,令tn为最新时刻,采用外推算法可得下一时刻的值xn+1。建立广义延拓外推模型:
| $ \left\{ {\begin{array}{*{20}{c}} {\min I\left( {{a_1},{a_2}, \cdots ,{a_j}} \right) = \min \sum\limits_{i = 0}^s {{{\left[ {{a_j}{g_j}\left( {{x_i}} \right) - {y_i}} \right]}^2}} }\\ {s.t.\;\;\;{a_j}{g_j}\left( {{x_e}} \right) = {y_e}} \end{array}} \right.. $ | (4) |
在上述模型中,由于插值点为最新采样点的值,为了克服这一点数值突变带来的误差,考虑建立改进的广义延拓模型:
| $ \left\{ {\begin{array}{*{20}{c}} {\min I\left( {{a_1},{a_2}, \cdots ,{a_j}} \right) = \min \sum\limits_{i = 0}^s {{{\left[ {{a_j}{g_j}\left( {{x_i}} \right) - {y_i}} \right]}^2}} }\\ {s.t.\;\;\;{a_j}{g_j}\left( {{x_e}} \right) = \frac{1}{p}\left( {\sum\limits_{e = s - p + 1}^s {{y_e}} } \right)} \end{array}} \right.. $ | (5) |
即选择最新的p个采样点的平均值作为约束,改进模型的解法与原模型的解法基本一致,但数据的平稳性更好,插值拟合曲线更平滑,外推精度更高。
2 全球定位系统精密星历的内插和外推方法 2.1 全球定位系统精密星历的解算方法考虑卫星的实际运行轨道会偏离无摄运行轨道,因此全球定位系统的星历参数通常采用一套扩展后的开普勒轨道参数,由16个参数组成,包括6个开普勒根数(
由文[10]提供的解算算法,可将卫星定位计算过程简要描述如下:
| $ \left[ {\begin{array}{*{20}{c}} {{X_i}}\\ {{Y_i}}\\ {{Z_i}} \end{array}} \right] = F\left( {\sqrt a ,e,\Omega ,\omega ,{i_0},{M_0},\Delta n,i,\dot \Omega ,{C_{{\rm{uc}}}},{C_{{\rm{rc}}}},{C_{{\rm{ic}}}},{C_{{\rm{us}}}},{C_{{\rm{rs}}}},{C_{{\rm{is}}}}} \right), $ | (6) |
其中,Xi,Yi,Zi为每个历元待求的卫星坐标。经过坐标变换和摄动校正,最终得到t时刻该卫星在WGS-84地心地固坐标系中的坐标计算矩阵:
| $ \left[ {\begin{array}{*{20}{c}} {{x_t}}\\ {{y_t}}\\ {{z_t}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{x'}_t}}&{ - {{y'}_t}}\\ {{{y'}_t}}&{{{y'}_t}}\\ 0&{{{y'}_t}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos {\Omega _t}}&{\sin {\Omega _t}}&0\\ {\sin {\Omega _t}\cos {i_t}}&{\cos {i_t}\cos {\Omega _t}}&{\sin {i_t}} \end{array}} \right], $ | (7) |
其中,x′t,y′t为信号发射时刻卫星在轨道平面的位置坐标;Ωt为信号发射时刻的升交点赤经;it为轨道倾角,均可由星历参数计算求得。
由以上求解过程可知,利用星历参数计算全球定位系统卫星在某一时刻的空间位置必须提供准确的星历数据,每定位一次需要的计算量也挺大。
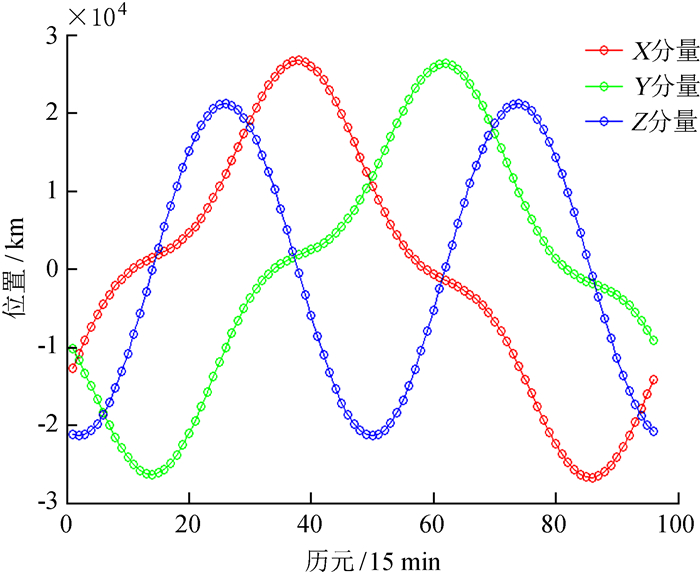
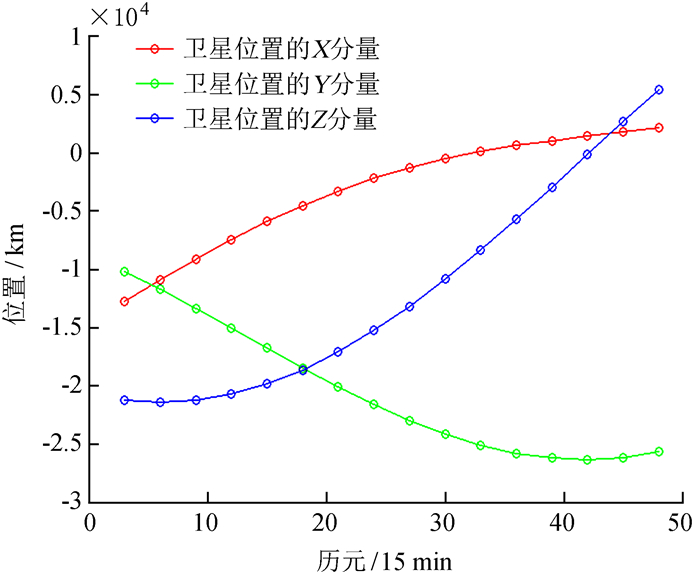
2.2 全球定位系统精密星历的插值可行性分析图 3中的3条曲线分别是某颗卫星的位置在WGS-84地心地固坐标系中的X, Y和Z分量随时间的变化情况,历元间隔为15 min,可见卫星的轨道位置呈周期性变化。如图 4,卫星位置的各分量在短时间内变化平滑,几乎呈线性变化。
|
| 图 3 长时间内卫星的空间位置 Figure 3 Space position of satellite over a long period of time |
|
| 图 4 短时间内卫星的空间位置 Figure 4 Space position of satellite in short time |
因此,卫星的一段轨道可以用一个以时间域的插值多项式表达[11],如果此逼近函数构造得当,那么这种插值方法不会引入很大的卫星位置误差,可避免2.1节所述的复杂计算方法,使计算量大幅度减少。
2.3 基于广义延拓的全球定位系统精密星历内插和外推方法利用广义延拓插值原理,对卫星位置与速度在WGS-84地心地固坐标系中的X,Y,Z分量分别分段建立广义延拓模型,在tk到tn这段时间内,以卫星位置在X方向上的分量为例,若在区间内取两端点作为先验点进行约束,则广义延拓插值模型为
| $ \left\{ \begin{array}{l} \min I\left( {{a_1},{a_2},{a_3}} \right) = \sum\limits_{k = 1}^n {{{\left[ {{a_1} + {a_2}{t_k} + {a_3}t_k^2 - {x_k}} \right]}^2}} \\ s.t.\left\{ \begin{array}{l} {a_1} + {a_2}{t_k} + {a_3}t_k^2 = {x_k}\\ {a_1} + {a_2}{t_n} + {a_3}t_n^2 = {x_n} \end{array} \right. \end{array} \right., $ | (8) |
其中,xk表示在插值区间左端点tk时刻卫星位置在WGS-84地心地固坐标系中X方向上的分量;xn表示在插值区间右端点tn时刻卫星位置在WGS-84地心地固坐标系中X方向上的分量;a1, a2, a3为待求系数;tk, tn是精密星历更新的时间点。
对上述模型展开求解,即由
| $ \left\{ {\begin{array}{*{20}{c}} {\frac{{\partial I}}{{\partial {a_1}}} = 0}&{\frac{{\partial I}}{{\partial {a_2}}} = 0}&{\frac{{\partial I}}{{\partial {a_3}}} = 0}&{\frac{{\partial I}}{{\partial {\lambda _1}}} = 0}&{\frac{{\partial I}}{{\partial {\lambda _2}}} = 0} \end{array}} \right., $ | (9) |
得到法方程CY=F,(9)式中,λ1, λ2为拉格朗日乘子,其中
| $ C = \left\{ {\begin{array}{*{20}{c}} {2\sum\limits_{k = 1}^n 1 }&{2\sum\limits_{k = 1}^n {{t_k}} }&{2\sum\limits_{k = 1}^n {{{\left( {{t_k}} \right)}^2}} }&1&1\\ {2\sum\limits_{k = 1}^n {{t_k}} }&{2\sum\limits_{k = 1}^n {{{\left( {{t_k}} \right)}^2}} }&{2\sum\limits_{k = 1}^n {{{\left( {{t_k}} \right)}^3}} }&{{t_1}}&{{t_n}}\\ {2\sum\limits_{k = 1}^n {{{\left( {{t_k}} \right)}^2}} }&{2\sum\limits_{k = 1}^n {{{\left( {{t_k}} \right)}^3}} }&{2\sum\limits_{k = 1}^n {{{\left( {{t_k}} \right)}^4}} }&{t_1^2}&{t_n^2}\\ 1&{{t_1}}&{t_1^2}&0&0\\ 1&{{t_2}}&{t_2^2}&0&0 \end{array}} \right\}, $ | (10) |
且Y={a1 a2 a3 λ1 λ2}T,F={
接着,由(5)式构造广义延拓外推模型:
| $ \left\{ \begin{array}{l} \min I\left( {{a_1},{a_2},{a_3}} \right) = \sum\limits_{k = 1}^n {{{\left[ {{a_1} + {a_2}{t_k} + {a_3}t_k^2 - {x_k}} \right]}^2}} \\ s.t.\;{a_1} + {a_2}{t_k} + {a_3}t_k^2 = \frac{1}{p}\left( {\sum\limits_{j = n - p + 1}^n {{x_j}} } \right) \end{array} \right., $ | (11) |
其中,变量含义见(8)式,p表示选用了最新p个卫星位置的X分量,取平均值作为外推模型约束。对此模型的解法如下:
| $ \left\{ \begin{array}{l} {a_1} = \frac{1}{m}\left( {\sum\limits_{j = n - p + 1}^n {{x_j}} } \right) - {a_2}{t_n} - {a_3}t_n^2\\ \frac{{\partial I\left( {{a_2},{a_3}} \right)}}{{\partial {a_2}}} = 0\\ \frac{{\partial I\left( {{a_2},{a_3}} \right)}}{{\partial {a_3}}} = 0 \end{array} \right., $ | (12) |
可得系数求解矩阵:
| $ \left[ {\begin{array}{*{20}{c}} {{a_2}}\\ {{a_3}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}\\ {{c_{21}}}&{{c_{22}}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{b_2}}\\ {{b_3}} \end{array}} \right], $ | (13) |
其中:
| $ \begin{array}{l} {c_{11}} = \sum\limits_{i = 1}^{n - 1} {\left( {t_i^2 - 2{t_i}{t_n} - t_n^2} \right)} ,\\ {c_{12}} = {c_{21}} = \sum\limits_{i = 1}^{n - 1} {\left( {t_i^3 - t_i^2{t_n} - {t_i}t_n^2 + t_n^3} \right)} ,\\ {c_{22}} = \sum\limits_{i = 1}^{n - 1} {\left( {t_i^4 - 2t_i^2t_n^2 + t_n^4} \right)} ,\\ {b_2} = \sum\limits_{i = 1}^{n - 1} {\left[ {{t_i}{x_i} - {t_i}\frac{1}{m}\left( {\sum\limits_{j = n - m + 1}^n {{x_j}} } \right) - {t_n}{x_i} + {t_n}\frac{1}{m}\left( {\sum\limits_{j = n - m + 1}^n {{x_j}} } \right)} \right]} ,\\ {b_3} = \sum\limits_{i = 1}^{n - 1} {\left[ {t_i^2{x_i} - t_i^2\frac{1}{m}\left( {\sum\limits_{j = n - m + 1}^n {{x_j}} } \right) - t_n^2{x_i} + t_n^2\frac{1}{m}\left( {\sum\limits_{j = n - m + 1}^n {{x_j}} } \right)} \right]} . \end{array} $ | (14) |
解得待求系数后,便可得到外推公式:
| $ {x_j} = {a_1} + {a_2}{t_j} + {a_3}t_j^2,j = n + 1,n + 2, \cdots $ | (15) |
同理可得卫星位置在其余各分量上的外推公式。
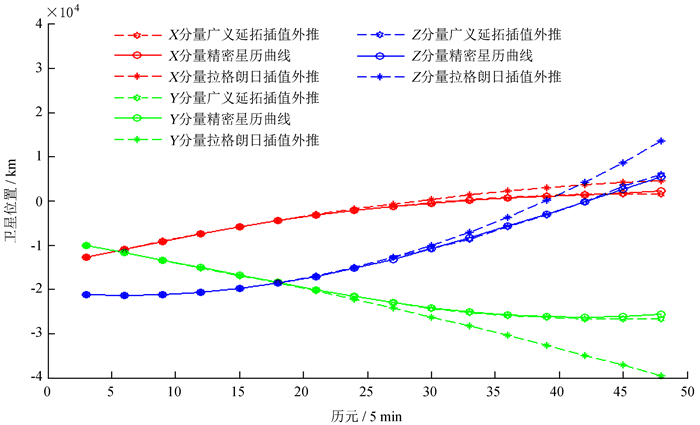
3 算例分析现验证广义延拓插值外推模型的推算效果,采用国际GNSS服务中心提供的2017年6月6日(即GPS 1952周)采样时间间隔为15 min的精密星历数据,选用的卫星为PRN15号。选取前4个采样数据作为先验采样点,以拉格朗日插值法作为参照,并与精密星历数据拟合的标准曲线对比,得到两种精密星历插值法的逼近效果如图 5。
|
| 图 5 两种精密星历插值法的插值外推效果对比 Figure 5 Comparison of interpolation and extrapolation effects of two precise ephemeris interpolation methods |
由图 5可见,当以1小时的精密星历作为先验点进行拟合逼近函数时,在1.5小时的时段内,拉格朗日插值法和广义延拓法构造的逼近函数与精密星历的拟合曲线基本吻合,而在1.5小时以后,广义延拓法的外推效果明显优于拉格朗日插值法。为了更直观地观察广义延拓法构造的模型精度,将X,Y,Z各分量的误差整合为位置误差e,
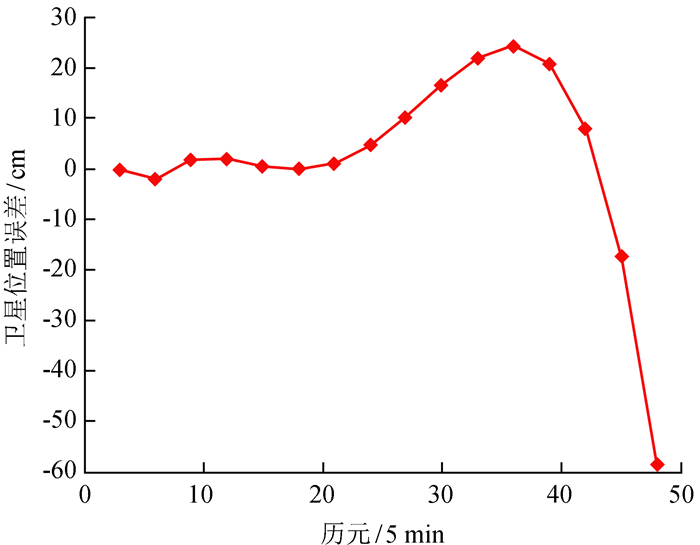
|
| 图 6 卫星位置随时间变化图 Figure 6 Chart of satellite position versus time |
由图 6可知,前4个比对点拟合的曲线为广义延拓内插效果,其插值的卫星位置误差小于5 cm,自第5个比对点开始为广义延拓的外推效果,可见广义延拓外推1小时左右的卫星位置误差小于10 cm,外推2小时的卫星位置误差小于20 cm,而在外推2小时以后,卫星位置误差开始迅速变大。
由于国际GNSS服务中心提供的精密星历误差精度为5 cm,因此,利用广义延拓法对全球定位系统精密星历的内插能够满足精度要求,而在利用广义延拓外推时,在30 min内能维持精度,在较长时间内也不会引入很大的位置误差。
4 结论采用广义延拓法对全球定位系统精密星历进行卫星位置内插时效果较好,可以将卫星的一段轨道用一个以时间为坐标的模型表达,使得计算卫星位置时在不损失精度的情况下,不再进行复杂冗长的步骤,极大地减少了计算量。此外,通过实例分析,广义延拓外推法能够保证外推1小时的精度满足要求,广义延拓内插法可获得全球定位系统任一时刻的精密星历数据。
| [1] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005. |
| [2] |
孙腾科. 基于拉格朗日与切比雪夫的精密星历插值研究[J]. 测绘与空间地理信息, 2014, 37(2): 33–37 Sun Tengke. The research of GPS precise interpolation methods based on Lagrange and Chebyshev[J]. Geomatics & Spatial Information Technology, 2014, 37(2): 33–37. |
| [3] |
汪威, 陈明剑, 闫建巧, 等. 北斗三类卫星精密星历内插方法比较分析[J]. 全球定位系统, 2016, 41(2): 60–65 Wang Wei, Chen Mingjian, Yan Jianqiao, et al. Three kinds of compass satellite precise ephemeris interpolation method analysis comparative[J]. GNSS World of China, 2016, 41(2): 60–65. |
| [4] |
王超, 郭际明, 周命端, 等. 高精度GPS数据处理中GAMIT批处理方法与实现[J]. 测绘信息与工程, 2012, 37(2): 10–12 Wang Chao, Guo Jiming, Zhou mingduan, et al. A method of GAMIT batch processing and its implementation in high precise GPS data processing[J]. Journal of Geomatics, 2012, 37(2): 10–12. |
| [5] |
雷雨, 赵丹宁, 高玉萍. 基于滑动式Lagrange插值方法的GPS精密星历内插分析[J]. 测绘工程, 2013, 22(2): 34–36 Lei Yu, Zhao Danning, Gao Yuping. Analysis of interpolation for GPS precise ephemeris using sleek Lagrange interpolation[J]. Engineering of Surveying and Mapping, 2013, 22(2): 34–36. |
| [6] |
柳笛, 逢淑涛, 董绪荣. IGS精密星历文件的读取及内插方法研究[J]. 全球定位系统, 2011, 36(5): 46–48 Liu Di, Pang Shutao, Dong Xurong. Read of precise ephemeris file and research on methods of interpolation[J]. GNSS World of China, 2011, 36(5): 46–48. |
| [7] | 施浒立, 颜毅华, 徐国华, 等. 工程科学中的广义延拓逼近发[M]. 北京: 科学出版社, 2005. |
| [8] |
魏彦飞, 耿建平, 施浒立, 等. 一种新的数据融合方法-广义融合法[J]. 天文研究与技术, 2016, 13(3): 318–325 Wei Yanfei, Geng Jianping, Shi Huli, et al. A new method of data fusion-the generalized fusion method[J]. Astronomical Research & Technology, 2016, 13(3): 318–325. |
| [9] |
耿建平, 衣伟, 刘成, 等. 基于广义延拓外推的单频周跳检测与修复方法[J]. 天文研究与技术, 2015, 12(2): 174–182 Geng Jianping, Yi Wei, Liu Cheng, et al. A new method for detection and correction of single-frequency cycle slips using data extrapolation based on the method of generalized extended interpolation[J]. Astronomical Research & Technology, 2015, 12(2): 174–182. |
| [10] | Jiang R B, Liu X Q. Using fourier series to fit the GPS precise ephemeris[C]//2010 International Conference on Computer Application and System Modeling (ICCASM 2010). 2010: 96-99. |
| [11] | Liu W P, Hao J M. A new interpolation method based on satellite physical character in using IGS precise ephemeris[J]. Geodesy and Geodynamics, 2014, 5(3): 29–33. DOI: 10.3724/SP.J.1246.2014.03029 |


