Chirp信号是一种频率随时间有规律连续变化的信号,它占用一段连续的频谱,相比于单频信号,具有更好的自相关性。早在20世纪50年代,贝尔实验室在改进雷达技术中利用Chirp信号优良的自相关特性实现脉冲压缩技术,提高了测距精度和接收信号的信噪比,从而提高了雷达分辨率和灵敏度,降低了发射功率[1-3]。从此,Chirp信号作为无线电应用中提高测量精度和信噪比的一种关键技术,在雷达、导航定位、空间探测、频谱测量和扩频通信等领域得到了广泛的应用[4]。
在天文研究中, 原子、分子和离子的辐射和吸收谱线特性中包含物质成分及其所处的环境信息,频谱测量成为一种重要的观测研究手段。行星大气的辐射和吸收频谱为红外波段,红外波段也称为太赫兹波段,高于常规电子设备的微波射频波段,低于光学设备的可见光波段,受器件性能的局限,行星大气的红外谱测量设备难以同时满足宽带和高精度频谱的实时测量,限制了行星大气科学的红外谱观测研究。根据光谱形态学的原理和大气模型,通过测量行星大气的辐射或吸收谱线的精确形状,可获得行星大气的成分、比例、密度、温度和压力等参数信息[5-7]。对红外谱线观测,通常采用外差接收的方法,将红外波段光谱信号通过红外前端设备变频到满足带宽要求的中频波段,使用高性能的后端处理设备获取宽带和高精度的谱形状,为实现此测量要求,曾研发了一些红外谱后端处理频谱仪,如自相关频谱仪(Autocorrelation Spectrometer)、声光频谱仪(Acousto Optical)、滤波器组频谱仪(Filter Bank)、快速傅里叶变换频谱仪等。但这些设备无法同时兼顾高精度和宽带实时测量的要求,或者存在工作不稳定和难以校准的缺点[5]。
20世纪60年代,文[1]从理论上提出了基于Chirp信号的脉冲压缩可用于实现傅里叶变换的数学原理,其将频谱测量转换为信号与Chirp信号的相乘和卷积运算。文[3, 5]使用电子器件实现了这一频谱测量设备,称之为Chirp变换频谱仪(Chirp Transform Spectrometer, CTS)。20世纪80年代,得益于声表面波滤波器(Surface Acoustic Wave, SAW)在信号处理中的应用,利用声表面波滤波器件实现了宽带线性Chirp信号生成与卷积运算。德国马普天文台运用声表面波滤波器件和Chirp信号测量频谱的原理,解决了传统的大气红外谱实时观测设备无法同时满足带宽和频谱精度要求的问题,首次研制成功了用于地球大气、行星大气和彗星大气的Chirp变换频谱仪。其接收采用超外差的方式,观测频率为几十GHz至几THz,带宽为几百MHz,重量、体积、功耗和稳定性等参数优良,特别适合安装在空间飞行器上使用。随后Chirp变换频谱仪的性能不断提升,已成功应用于毫米波大气探测(Millimeter wave Atmospheric Sounder, MAS),Rosetta探测器微波遥感设备(Microwave Instrument for Rosetta Orbiter, MIRO),德国太赫兹大气探测接收机(German REceiver for Astronomy at Terahertz frequency, GREAT)等项目[5-9]。
Chirp变换频谱仪采用声表面波滤波器实现了宽带Chirp信号的生成和卷积运算, 相比于其他的红外后端频谱测量设备,具有结构简单、测量带宽宽、测量精度高、功耗小和可靠性高等优点[5, 10]。但是声表面波滤波器件在插入损耗、色散效应、带宽和频率灵活性方面的问题,限制了基于声表面波滤波器件的Chirp变换频谱仪性能的进一步提高[5]。随着数字电子技术的发展, 马普天文台利用直接频率合成(Direct Digital Synthesis, DDS)芯片生成线性Chirp信号, 改善了Chirp变换频谱仪的性能。使用直接频率合成芯片可以生成与器件失真后相匹配的预失真线性Chirp信号,校正模拟电路部分的色散效应,并且直接频率合成芯片可灵活地改变Chirp信号的带宽和频点。基于高性能的直接频率合成芯片可以生成带宽为1GHz的线性Chirp信号,从而实现215MHz带宽的实时频谱测量[6, 9, 11]。还有研究人员使用矢量信号发生器生成了一种1GHz带宽的线性Chirp信号,用于高精度的分子光谱测量[12]。
在我国Chirp变换频谱仪早期也被称为“声表面波频谱仪”,“声表面波线性调频变换功率谱仪”[13-18]。中国科学院声学研究所曾为马普天文台的Chirp变换频谱仪研制了Chirp信号带宽为400MHz、600MHz、800MHz的专用表面波滤波器件[19-20]。20世纪90年代我国探讨了Chirp变换频谱仪在射电天文中观测分子谱线的可行性,论证了在云南天文台和紫金山天文台毫米波射电望远镜后端信号处理中应用Chirp变换频谱仪[13-14]。Chirp变换频谱仪也应用于我国乌鲁木齐25m射电望远镜开展水脉泽观测研究[21-22]。
本文综述基于Chirp信号和脉冲压缩技术的Chirp变换频谱仪,首先介绍Chirp信号和基于Chirp信号的脉冲压缩技术,给出基于Chirp信号和脉冲压缩技术实现频谱测量的数学原理,进而描述了Chirp变换频谱仪的原理,然后介绍了Chirp变换频谱仪基于声表面波滤波器实现的方法,Chirp变换频谱仪在行星大气和彗星红外谱测量中的具体应用,以及Chirp变换频谱仪的发展历程和改进方向。
1 Chirp信号与脉冲压缩 1.1 Chirp信号介绍Chirp信号的特征是频率随时间连续变化。频率随时间线性增加或减小的信号称为线性Chirp信号,频率随时间指数变化的信号称为指数Chirp信号①。Chirp信号在大自然中广泛存在,如多普勒效应、引力波以及其英文本意所指的鸟鸣等。
①http://en.wikipedia.org/wiki/Chrip
线性Chirp信号在天文观测的电子设备中较常使用,其频率随时间线性变化,频率表达式为
| $ f\left( t \right) = {f_0} + kt, $ | (1) |
其中,
| $ \phi \left( t \right) = {\phi _0} + 2\pi \left( {{f_0}t + \frac{k}{2}{t^2}} \right), $ | (2) |
相位ϕ(t)是时间t的二次函数,线性Chirp也常称为二项式相位信号。
在一个频率变化周期内,线性Chirp信号的时域表达式为
| $ s\left( t \right) = {\rm{exp}}\left\{ {- {\rm{j}}\left[{{\phi _0} + 2\pi \left( {{f_0}t + {\rm{ }}\frac{k}{2}{t^2}} \right)} \right]} \right\}, $ | (3) |
信号的时域波形和频率随时间变化的波形如图 1。从图 1可以看出,线性Chirp信号随时间呈周期递减的震荡变化,波形随时间逐渐变密,频率由低到高呈线性增加,周期性扫频。因此,线性Chirp信号也常作为电子设备的扫频信号。
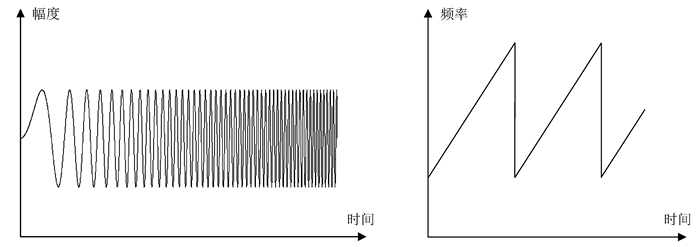
|
| 图 1 线性Chirp信号及其频率随时间的变化 Figure 1 A linear Chirp signal and it′s spectrogram |
指数Chirp信号的频率与时间的关系可以表示为
| $ f\left( t \right) = {f_0}{k^t}, $ | (4) |
其中,f0为初始频率;k为决定频率呈指数变化率的底数。指数Chirp信号的相位为
| $ \phi \left( t \right) = {\phi _0} + 2\pi {f_0}\left( {\frac{{{k^t}-1}}{{{\rm{ln}}k}}} \right). $ | (5) |
在一个频率变化周期内,指数Chirp信号的时域表达式为
| $ s\left( t \right) = {\rm{exp}}\left\{ {- {\rm{j}}\left[{{\phi _0} + 2\pi {f_0}\left( {\frac{{{k^t}-1}}{{{\rm{ln}}k}}} \right)} \right]} \right\}. $ | (6) |
图 2给出了指数Chirp信号的时域波形和频率随时间变化的曲线。从图 2可以看出,指数Chirp信号的频率由低到高呈指数增加,且周期性重复,频率变化速度比线性Chirp更快。
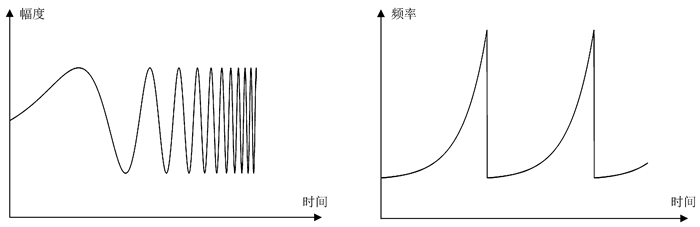
|
| 图 2 指数Chirp信号及其频率随时间变化 Figure 2 An exponential Chirp signal and it′s spectrogram |
脉冲压缩的原理是在信号处理中将一个特征信号调制到发射信号上,在接收端用相同的特征信号做相关以检测发射信号,调制特征信号增加了信号的自相关性,使信号更易于被检测和测量。脉冲压缩常应用于雷达、声呐和回波检测中,用于增加测距精度和提高检测信噪比[4]。
例如在雷达中检测矩形脉冲信号的回波,如果脉冲宽度为T,则相关函数是宽度为2T的三角函数,如图 3。如果两个回波的间隔小于T,则两个相关函数将混叠在一起无法区分。

|
| 图 3 基于矩形脉冲的回波检测 Figure 3 Echo detection using rectangular pulse signal |
若采用脉冲压缩技术,在发射信号上调制一个带宽为Δf的线性Chirp信号,在接收端用相同的Chirp信号做检测。Chirp信号的自相关函数可表示为
| $ \left\langle {{S_c}, {S_c}} \right\rangle \left( t \right) = T\Lambda \left( {\frac{t}{T}} \right){\rm{sinc}}\left[{{\rm{\pi }}\Delta ft\Lambda \left( {\frac{t}{T}} \right)} \right]{\rm{ }}{e^{{\rm{j}}2{\rm{\pi }}{f_0}t}}, $ | (7) |
它是一个sinc函数,主瓣宽度为
|
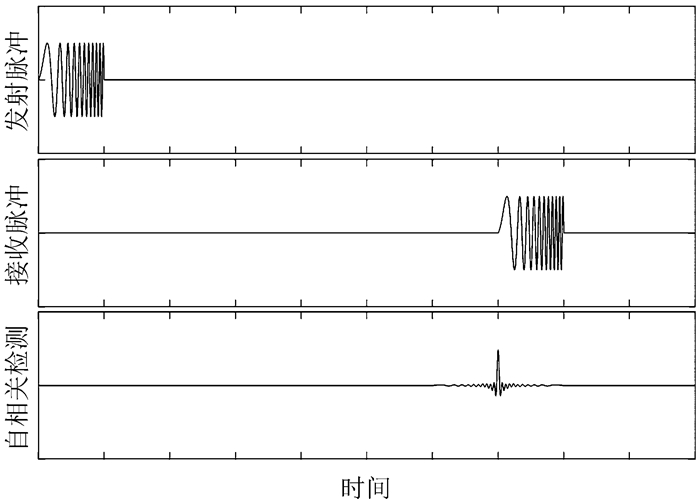
| 图 4 基于Chirp信号的脉冲压缩的回波检测 Figure 4 Echo detection by pulse compression using Chirp signal |
相比矩形脉冲信号的回波检测,图 4中使用Chirp信号脉冲压缩技术的自相关检测信号的信噪比和分辨率更高。脉冲的宽带与Chirp信号的频率范围成反比关系,即单位时间内Chirp信号频率范围越宽,相关峰越尖锐,测量精度越高。
2 Chirp变换频谱仪 2.1 基于Chirp信号实现频谱测量原理使用Chirp信号测量频谱的原理可以由傅里叶变换导出。傅里叶变换可表示为
| $ F\left( \omega \right) = \int_{-\infty }^{ + \infty } {s\left( t \right){e^{-{\rm{j}}\omega t}}{\rm{d}}t}, \omega = 2\pi f, $ | (8) |
其中,s(t)为时域信号;f为信号频率;ω为信号角频率。采用线性Chirp信号,假设f=μτ,μ为频率随时间的变化率;τ为频率变化的时间,则傅里叶变换可表示为
| $ F\left( \omega \right) = \int_{-\infty }^{ + \infty } {s\left( t \right){e^{-{\rm{j}}2{\rm{\pi }}\mu \tau t}}{\rm{d}}t}, $ | (9) |
其中,2τt可以分解为
| $ 2\tau t = {t^2} + {\tau ^2}-{\left( {t-\tau } \right)^2}, $ | (10) |
将(10) 式代入(9) 式,傅里叶变换可以表示为
| $ F\left( \omega \right) = {e^{-{\rm{j\pi }}\mu {\tau ^2}}}\int_{-\infty }^{ + \infty } {s\left( t \right){e^{-{\rm{j\pi }}\mu {t^2}}}{e^{{\rm{j\pi }}\mu \left( {t - \tau } \right)2}}dt} . $ | (11) |
假设
| $ F\left( \omega \right) = {e^{- {\rm{j\pi }}\mu {\tau ^2}}}\cdot{\rm{ }}\left[{\left( {s\left( t \right)\cdot{e^{-{\rm{j\pi }}\mu {t^2}}}} \right) * h\left( t \right)} \right]. $ | (12) |
即除去相位差
使用上述原理,应用线性Chirp信号的相乘和卷积运算可以实现傅里叶变换,计算信号的频谱。
2.2 Chirp变换频谱仪的原理基于线性Chirp信号的脉冲压缩实现频谱测量设备原理如图 5[5-7]。
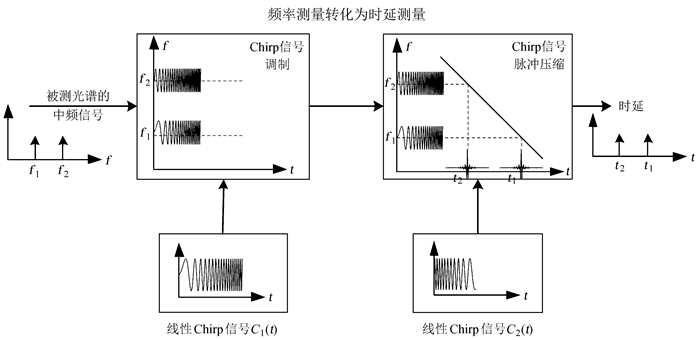
|
| 图 5 Chirp变换频谱仪的原理 Figure 5 The principle of CTS |
图 5中输入信号为红外光谱信号下变频后的中频信号,带宽为f2-f1。根据Chirp信号实现傅里叶变换的原理,将生成的线性Chirp信号C1(t)调制到该中频信号上,将Chirp调制后的信号与一个频率变化率相反的Chirp信号C2(t)做卷积,以实现基于Chirp信号的脉冲压缩检测。在这个过程中,中频信号的频率改变了Chirp信号的相关峰出现的时间偏差,相应的相关峰时延对应被测中频信号的频率。对于一个线性系统,信号可分解为各频率分量的线性相加,测量时延信号形状,即可实时测量出对应的红外谱形状。Chirp变换频谱仪将信号频率的测量转换为时延信号的测量。
根据图 5的原理,一种Chirp变换频谱仪的实现框图如图 6[9]。图 6中Chirp信号发生器产生线性Chirp信号,经过倍频、滤波和放大后,经过混频器与被测中频信号调制,得到有频率偏移的Chirp信号。通过声表面波滤波器实现Chirp信号的卷积运算,输出带时间偏差的线性Chirp信号相关峰信号,通过数据采集存储和信号分析,测量相关峰信号的时延,从而计算出对应的被测信号频谱。

|
| 图 6 Chirp变换频谱仪的实现框图 Figure 6 A block diagram of CTS |
从20世纪80年代首次研制并应用开始,Chirp变换频谱仪已装备于地基、机载和星载观测设备中,对地球大气、行星大气、彗星和星际介质分子开展了红外谱线测量。
Chirp变换频谱仪最早应用于地基大气探测,测量地球中层大气中臭氧、水蒸气和二氧化碳等分子辐射谱线,得到其分子密度大气剖面,研究在大气中的运动和传输。在挪威的Arctic Lidar中层大气观测台(Arctic Lidar Observatory for Middle Atmosphere Research, ALOMAR)使用Chirp变换频谱仪对地球中层大气中水蒸气分子光谱观测已进行了一个太阳周的常规观测(1996~2006),研究了地球中层大气的季节变化以及与太阳活动的相关性,并为完善地球大气模型和大气辐射谱形状理论积累了数据[23-24]。
同温层红外天文台(Stratospheric Observatory For Infrared Astronomy, SOFIA)使用2.5m红外反射式望远镜,搭载多个波段的红外观测设备,用于研究行星表面和大气组成、彗星组成、演化和结构、星际物质的特征和化学性质以及恒星和其他天体的组成。同温层红外天文台使用一架波音747SP飞机,运行于15km高空,可以避开地球大气的水蒸气对红外谱的吸收干扰,具有更高的灵敏度,能探测更多的分子谱线,且可以对观测天体开展连续观测。同温层红外天文台上运行的德国太赫兹大气探测接收机基于Chirp变换频谱仪实现,用于对1.6~1.9THz、2.6THz和4.7THz 3个频段的碳离子、氘氢分子和氧原子等谱线观测。应用于同温层红外天文台的Chirp变换频谱仪对Chirp信号发生器部分做改进,使用直接频率合成数字芯片生成预失真的宽带线性Chirp信号,用于修正模拟电路部分的色散效应,提高了测量性能[8-9]。
欧洲空间局的Rosetta彗星探测器是首次成功实现环绕彗星并登陆彗星的深空探测器,用于探索彗星结构、太阳系形成和早期信息以及地球上水的来源与彗星的关联。Rosetta于2004年3月发射,2014年8月进入67P/Churyumov-Gerasimenko彗星轨道,2016年9月结束探测任务。Rosetta搭载的MIRO观测设备基于Chirp变换频谱仪实现,用于测量慧尾和彗星蒸发气体中水、氨气和二氧化碳等气体分子辐射的红外谱线形状,从而得到其成分、密度、风速、温度、气压等信息。MIRO也是首个用于深空探测的亚毫米波外差测量设备[25]。
我国在射电天文观测中应用Chirp变换频谱仪开展了射电天文星际分子谱线观测研究。乌鲁木齐25m射电望远镜基于Chirp变换频谱仪的分子谱线观测系统对水脉泽的观测已发现十几个可能的水脉泽源[21-22]。Chirp变换频谱仪也应用在紫金山天文台青海站13.7m射电天文望远镜的毫米波测量系统中,对22GHz水分子脉泽源开展观测,其中心频率为529MHz,实时带宽为39.9MHz,分辨率≤40kHz[15]。
2.4 Chirp变换频谱仪的发展趋势Chirp变换频谱仪从20世纪80年代初开始研制,到80年代中期实际应用,根据不同的项目应用需求,在1983~2004实现的Chirp变换频谱仪的参数指标如表 1[5-7]。
| 参数 | 1983 | 1984 | 1985 | 1987 | 1991 | 1992 | 1996 | 2004 |
| 中频频率/MHz | 180 | 300 | 1350 | 300 | 300 | 1350 | 1350 | 2100 |
| 测量带宽/MHz | 25 | 22 | 40 | 40 | 40 | 40 | 178 | 215 |
| 谱测量精度/kHz | 500 | 150 | 50 | 50 | 22 | 50 | 43 | 41.7 |
| 动态范围/dB | 18 | 27 | 26 | 15 | 30 | 30 | 29 | 30 |
| 线性范围/kHz | 20 | 8 | 1 | 1 | 1 | 1 | 2 | 7 |
| 功耗/W | 420 | 520 | 530 | 430 | 50 | 30 | 14 | 32 |
| 质量/kg | 22 | 20 | 20 | 25 | 10 | 10 | 2.3 | 14 |
从表 1指标数据可以看出,随着时间的推移,Chirp变换频谱仪的中频频率、测量带宽、频谱测量精度、信号测量动态范围均有提高,功耗和质量也得到显著改善。这是由于声表面波滤波器件、射频器件和数字处理器件性能的提高,中频频率和测量带宽的提高也得益于信号采样率和数据处理速度的提高。进入20世纪90年代,Chirp变换频谱仪的功耗和质量得到1~2个量级的显著改善。1996年以后研制的Chirp变换频谱仪,相比之前,在测量带宽上有了4倍以上的提升。深空探测对Chirp变换频谱仪的功耗和质量提出了更为严格的要求。搭载于Rosetta深空探测器的MIRO-CTS,质量2.3kg、功耗14W。2004年搭载于同温层红外天文台的德国太赫兹大气探测接收机,最高测量频率为4.7THz,直接频率合成的应用使得Chirp变换频谱仪的频谱测量带宽为215MHz,精度为41.7kHz,保证了行星大气和彗星大气的红外波段谱线形状测量的效率和精度,为大气模型提供了丰富准确的数据。
近年来,信息化潮流促进了电子技术的普及应用,尤其是数字处理相关技术的发展日新月异。Chirp变换频谱仪第一次采用直接频率合成生成宽带Chirp信号以来,十几年过去了,我们相信把性能更好的声表面波滤波器件和其它新型数字处理技术引入Chirp变换频谱仪中,一定能够进一步提升Chirp变换频谱仪的性能,满足更宽频带和更高精度的红外谱线实时观测需求,并实现设备的低功耗和高稳定性,为我国的行星大气、彗星、星际介质研究提供更好的观测手段。如基于现场可编程门阵列实现快速傅里叶变换可与Chirp变换频谱仪测量频谱结合使用,射频信号的数字采集回放技术和软件无线电技术[26-28],静磁表面波滤波器技术等都可尝试应用于Chirp变换频谱仪[29]。特别是随着微电子技术的进步,可以制造出高速率低功耗的数字自相关器,数字器件相比声表面波滤波器等模拟器件有更好的灵活性和性能,采用数字自相关器实现的红外谱后端测量设备可能逐步替代基于声表面波滤波器件的Chirp变换频谱仪。需要指出的是,对于稳定性和功耗要求严格的机载和星载应用,基于声表面波滤波器实现的Chirp变换频谱仪仍然是一种有效的测量手段。
3 结语Chirp信号具有良好的自相关特性,基于Chirp信号和脉冲压缩测量频谱原理实现的Chirp变换频谱仪用于测量红外波段分子谱线形状,为获取行星和彗星大气的成分、比例、密度、温度和压力等参数提供了测量手段。Chirp变换频谱仪使用声表面波滤波器件实现Chirp信号的生成和卷积运算,得益于声表面波滤波器件的优良性能,Chirp变换频谱仪相比于自相关频谱仪、声光频谱仪、滤波器组频谱仪、快速傅里叶变换频谱仪等频谱测量设备,具有体积小、功耗小和可靠性高等优点。直接频率合成器件的应用使得Chirp变换频谱仪的性能进一步提高。Chirp变换频谱仪已装备于地基、机载和星载探测设备中,用于测量地球大气、行星大气、彗星以及星际介质分子的谱线形状。
随着电子技术的发展,可以将直接频率合成、现场可编程门阵列等高性能数字器件引入Chirp变换频谱仪中,用于生成带宽更宽的Chirp信号,修正系统非线性误差,以提高测量性能。射频信号的数字采集回放技术和软件无线电技术,静磁表面波滤波器件等技术,也可以尝试应用到Chirp变换频谱仪中。基于数字芯片实现的快速傅里叶变换频谱仪在带宽和频谱精度性能上也不断提高,可与Chirp变换频谱仪结合使用。
基于最新的数字器件和声表面波滤波器件,我国可以研制新型的Chirp变换频谱仪,实现实时、更宽频段和更高精度的红外谱线测量指标,为我国的地球大气、行星大气、彗星和星际介质研究提供更好的观测手段,也为我国未来的深空探测和机载红外天文观测项目提供技术储备。
| [1] | Klauder J R, Price A C, Darlington S, et al. The theory and design of chirp radars[J]. The Bell System Technical Journal, 1960, 39(4): 745–808. DOI: 10.1002/bltj.1960.39.issue-4 |
| [2] | Cook C E. Pulse compression, key to more efficient radar transmission[C]//Proceedings of the IRE. 1960, 48(3):310-316. |
| [3] | Darlington S. Demodulation of wide band low power FM signals[J]. The Bell System Technical Journal, 1964, 43(1): 339–374. DOI: 10.1002/bltj.1964.43.issue-1 |
| [4] | Djuric P M, Kay S M. Parameter estimation of chirp signals[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1990, 38(12): 2118–2126. DOI: 10.1109/29.61538 |
| [5] | Hartogh P. Present and future chirp transform spectrometers for microwave remote sensing[C]//Proceedings of the SPIE. 1997:328-339. |
| [6] | Villanueva G L. The high resolution spectrometer for SOFIA-GREAT:instrumentation, atmospheric modeling and observations[D]. Germany:Freiburg University, 2004. http://adsabs.harvard.edu/abs/2003EAEJA.....2522V |
| [7] | Lucas Paganini. Power spectral density accuracy in chirp transform spectrometers[D]. Germany:Freiburg University, 2008. http://pubman.mpdl.mpg.de/pubman/faces/viewItemOverviewPage.jsp?itemId=escidoc:1898501 |
| [8] | Villanueva G, Hartogh P. The high resolution chirp transform spectrometer for the SOFIA-GREAT instrument[J]. Experimental Astronomy, 2004, 18: 77–91. DOI: 10.1007/s10686-005-9004-3 |
| [9] | Villanueva G L, Hartogh P, Reindl L. A digital dispersive matching network for SAW devices in Chirp Transform Spectrometers[J]. IEEE Transactions on Microwave Theory and Techniques, 2006, 54(4): 1415–1424. DOI: 10.1109/TMTT.2006.871244 |
| [10] | Hartogh P, Hartmann G. A high-resolution chirp transform spectrometer for microwave measurements[J]. Measurement Science & Technology, 1990, 1(1): 592–595. |
| [11] | Güsten R, Huebers H W, Graf U U, et at. GREAT-the first generation German heterodyne receiver for SOFIA[C]//Proceedings of SPIE. 2003:23-30. |
| [12] | Mani D, Bhat V, Vinoy K J, et al. Towards a broadband chirped pulse Fourier transform microwave spectrometer[J]. Indian Journal of Physics, 2012, 86(3): 225–235. DOI: 10.1007/s12648-012-0043-0 |
| [13] |
杜鸿, 苏步美. 云台射电频谱仪预研[J]. 云南天文台台刊, 1993(1): 25–31 Du Hong, Su Bumei. Investigation of radio spectrographs for the Yunnan Observatory[J]. Publications of Yunnan Observatory, 1993(1): 25–31. |
| [14] |
徐之材. 紫金山天文台新建的毫米波射电望远镜[J]. 电波科学学报, 1991(Z1): 22–25 Xu Zhicai. The new millimeter wave radio telescope built by Purple Mountain Observatory[J]. Chinese Journal of Radio Science, 1991(Z1): 22–25. |
| [15] |
陈东培, 宫俊杰, 周献文, 等. 一种新型射电天文频谱仪——声表面波频谱仪[J]. 天体物理学报, 1993, 13(1): 85–91 Chen Dongpei, Gong Junjie, Zhou Xianwen, et al. A new type of radio astronomical spectrometer——SAW spectrometer[J]. Acta Astrophysica Sinica, 1993, 13(1): 85–91. |
| [16] |
陈东培, 宫俊杰, 周献文, 等. 实用声表面波线性调频变换功率谱仪设计与分析的一些问题[J]. 声学学报, 1991, 16(2): 81–90 Chen Dongpei, Gong Junjie, Zhou Xianwen, et al. Problems in design and analysis of practical SAW CZT spectrometer[J]. Acta Acustica, 1991, 16(2): 81–90. |
| [17] |
陈东培, 宫俊杰, 周献文, 等. 实用宽带高分辨率声表面波线性调频变换功率谱仪[J]. 声学学报, 1991, 16(1): 37–46 Chen Dongpei, Gong Junjie, Zhou Xianwen, et al. A practical spectrometer based on SAW chirp z transform[J]. Acta Acustica, 1991, 16(1): 37–46. |
| [18] |
陈东培, 宫俊杰. SAW线性调频变换实时功率谱分析技术中测频温度特性分析[J]. 声学学报, 1990, 15(2): 121–129 Chen Dongpei, Gong Junjie. Analysis on dependence of frequency determination upon temperature in SAW-based real time chirp z transformation processor[J]. Acta Acustica, 1990, 15(2): 121–129. |
| [19] | Zhang Yuxing, Gong Junjie, Zhou Xianwen, et al. High-resolution spectrometer systems based on SAW chirp filter[C]//Ultrasonics Symposium, IEEE Xplore. 1997:89-92. |
| [20] | Gong Junjie, Zhang Yuxing, Zhou Xianwen, et al. Wide bandwidth SAW chirp filters with improved magnitude response[C]//Proceedings of the IEEE Ultrasonics Symposium. 2006:1895-1898. |
| [21] |
郑兴武, 加尔肯, 周建军. 乌鲁木齐25m射电望远镜首次水脉泽观测[J]. 中国科学(A辑), 2001, 31(3): 267–271 Zheng Xingwu, Jerken Esimbek, Zhou Jianjun. The first observation of water maser at Urumchi Astronomical Observatory[J]. Science in China (Series A), 2001, 31(3): 267–271. |
| [22] | 张晋, 王娜, 艾力·伊, 等.乌鲁木齐25m射电望远镜的单天线观测研究[J].天文学进展, 2000, 18(4):271-282. Zhang Jin, Wang Na, Esamdin Ali, et al. Single dish astrophysics observations at Urumchi Astronomical Observatory[J]. Progress in Astronomy, 2000, 18(4):271-282. |
| [23] | Hartogh P, Sonnemann G, Grygalashvyly M, et al. Water vapor measurements at ALOMAR over a solar cycle compared with model calculations by LIMA[J]. Journal of Geophysical Research Atmospheres, 2010, 115(D1): 736–744. |
| [24] | Hartogh P, Jarchow C. Millimeter wave detection of mesospheric ozone using a high resolution Chirp Transform Spectrometer backend[C]//Surface and Atmospheric Remote Sensing:Technologies, Data Analysis and Interpretation. 1994:3-5. |
| [25] | Ulkisl S, Frerkingl M, Crovisier J, et al. MIRO:Microwave Instrument for Rosetta Orbiter[J]. Space Science Reviews, 2007, 128(1): 561–597. |
| [26] |
吴亚军, 刘庆会, 李娟, 等. 上海天文台65m射电望远镜谱线观测及数据校准[J]. 天文研究与技术, 2017, 14(1): 1–7 Wu Yajun, Liu Qinghui, Li Juan, et al. Spectral line observation and data calibration of Tianma 65m Radio Telescope[J]. Astronomical Research & Technology, 2017, 14(1): 1–7. |
| [27] |
印琪骏, 朱亮, 何乐生, 等. 基于高性能芯片的射电天文厘米-分米波谱线观测方法[J]. 天文研究与技术, 2017, 14(1): 103–109 Yin Qijun, Zhu Liang, He Lesheng, et al. A new method to observe radio astronomy signal:centimeter-decimeter spectral line——based on highperformance integrated circuit[J]. Astronomical Research & Technology, 2017, 14(1): 103–109. |
| [28] |
托乎提努尔, 张海龙, 王杰. 基于CUDA的射电天文多相滤波器组设计[J]. 天文研究与技术, 2017, 14(1): 117–123 Tohtonur, Zhang Hailong, Wang Jie. A design of polyphase filter bank for radio astronomy based on CUDA[J]. Astronomical Research & Technology, 2017, 14(1): 117–123. |
| [29] | Manuilova S A, Forsb R, Khartsevc S I, et al. Pulsed laser deposited Y3Fe5O12 films for magnetostatic wave band pass filters[J]. Solid State Phenomena, 2009, 152-153: 377–380. DOI: 10.4028/www.scientific.net/SSP.152-153 |


