2. 中国科学院月球与深空探测重点实验室, 北京 100012;
3. 中国科学院大学, 北京 100049;
4. 杭州电子科技大学, 浙江杭州 310018
2. Key Laboratory of Lunar and Deep Space Exploration, Chinese Academy of Sciences, Beijing 100012, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. University of Electronic Science and Technology of Hangzhou, Hangzhou 310018, China
如今射电望远镜朝着大口径、高频段的方向发展,其指向精度的要求变得越来越严格。指向精度是衡量射电望远镜性能的重要指标之一,一般要求指向偏差小于天线半功率宽度(HPBW)的10%[1]。指向精度主要受重力变形、温度、风载、轨道变形等因素的影响,除了天线刚建好时的硬件校准外,最常用的精度修准方法是用软件对其进行误差补偿。目前天线的修正大多采用线性指向模型(Linear-PM),即通过对选定射电源的观测得到指向偏差实验样本,从方位、俯仰坐标及方位、俯仰偏差数据出发,求出观测数据的最佳拟合曲面,得到天线指向的误差修正函数表达式[2, 3]。
线性指向模型只考虑了一般线性偏差,而忽略了诸如风载、轨道变形等因素引起的非线性偏差对天线指向的影响,忽略了各分量之间的耦合关系,因此对望远镜指向精度的提高有一定的限制,需要经常对望远镜进行指向校准实验。对此,文[4]提出将测量得到的误差数据直接存入天线控制计算机,经差值进行实时改正,由于测量点在天空中分布比较稀疏,几何逼近性不很理想;文[5]提出考虑非线性方位轴倾斜误差的望远镜指向修正模型,通过数学方法用一阶傅里叶函数模拟方位轴倾斜与方位的函数关系,但数学模拟的方法与实际情况不能完全吻合;文[6]提出基于最小二乘支持向量机的天线指向偏差模型,该模型在核函数和控制参数选择、综合环境影响因素的实验验证方面需进一步研究。综合上述方法的局限和不足,本文针对大型轮轨式射电望远镜,结合轨道水平测量实验,提出一种考虑由轨道不平度引起的方位轴非线性倾斜偏差的指向修正方法。
1 指向误差修正模型 1.1 线性修正方法目前,国内外大型射电望远镜指向修正数学模型大多采用线性指向模型,其修正公式为[7, 8, 9]
| $\left\{ \begin{array}{l} \delta A = {C_1} - {C_3}\cos A\tan E - {C_4}\sin A\tan E + {C_5}\tan E - {C_6}{\mathop{\rm secE}\nolimits} \\ \delta E = {C_2} + {C_3}\sin A - {C_4}\cos A + {C_7}\cos E - {C_8}\cot E \end{array} \right.$ | (1) |
其中,δA、δE为对指定射电源观测分别得到方位、俯仰偏差数据;A、E为天线方位、俯仰坐标;C1为方位零点差; C2为俯仰零点差;C3为方位轴倾斜东西误差;C4为方位轴倾斜南北误差;C5为俯仰轴与方位轴不正交误差;C6为天线电轴与俯仰轴不正交误差;C7为天线重力变形误差;C8为大气折射残余误差[8, 9]。
1.2 考虑轨道不平度非线性误差的修正方法天线的轨道不平度引起方位轴的摇摆,导致倾斜误差系数C3、C4随方位A的变化而变化[5]。图 1反映了考虑轨道不平度的射电望远镜指向修正过程:通过实验测得天线全轨水平度,用有限元方法仿真并拟合C3、C4与方位A的函数关系C3(A)、C4(A),进而得到方位、俯仰非线性偏差dA1、dE1;同时,记录天线俯仰轴角测量单元因轨道的变形而产生的测量偏差dE2。应用天线指向实验测量的指向初始偏差δA、δE减去dA1、dE1+ dE2为考虑轨道非线性误差后的方位、俯仰修正误差样本,然后用该误差样本进行望远镜指向修正,得到指向辨识参数和校准后的指向残差均方差。

|
| 图 1 考虑轨道不平度的射电望远镜指向修正流程图 Fig. 1 A flowchart of calibration of radio-telescope pointing by including correction for roughness of the telescope rail |

|
| 图 2 密云50 m射电望远镜轨道结构 Fig. 2 A picture of a part of the rail track of the Miyun 50m radio telescope |
国家天文台50 m射电望远镜是我国探月工程中负责科学数据接收和探测器VLBI精密测轨任务的重要设备,坐落于北京市密云水库北岸,2007年建成使用,天线采用轮轨式方位旋转结构,轨道直径32.5 m,单轨水平度≤0.25 mm,全轨水平度要求≤0.8 mm,轨道基础3年不均匀沉降小于1 mm,天线指向精度不超过19″(RMS)。
2.1 轨道不平度的测量50 m天线的轨道不平度测量实验采用徕卡NI007型高精度水准仪测量设备。测量方法如图 3[10],将水准尺支架通过磁性作用吸附在滚轮轴承支架上,水准尺位于一组滚轮的对称线上,利用水准仪提供的水平视线,借助带有分划的水准尺,记录水准尺上测得的高度,特制水准尺随着滚轮绕中心枢轴转动,测量时每转动一个角度,测量一次,直到完成全轨的测量,轨道的全轨不平度随之测得。实验测量过程中选取每3°一个测量点,共测量全轨120个点的水平高度值。

|
| 图 3 轨道不平度测量过程 Fig. 3 A picture showing our measuring of the roughness of the rail track of the Miyun 50m radio telescope |
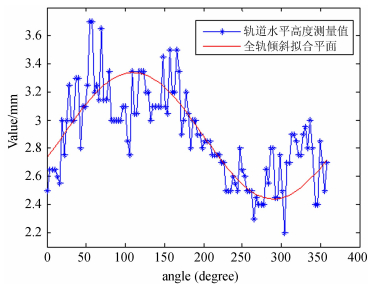
测量结果如图 4,其中实线部分为根据已知点和测得的高差,用最小二乘法进行平面拟合后的轨道水平值。由测量结果可知,全轨最低处出现在天线方位角303.9°处,为2.2 mm,全轨最高处出现在天线方位角54.9°处,为3.7 mm。全轨水平度为1.5 mm,超过0.8 mm的全轨水平度要求。
|
| 图 4 全轨水平测量值及线性拟合曲线 Fig. 4 Our measured track-elevation values along the entire rail track of the 50m telescope. The red curve is a linear-regression fit to the values |
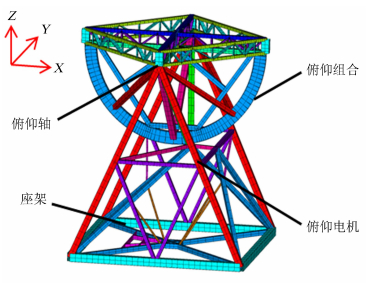
依据50 m天线模型应用ANSYS软件结构分析模块进行建模。需要建立的模型部分包括天线座架(含俯仰电机)、俯仰大齿轮与十字通轴组合(含俯仰轴),由于天线主反射体(包括主面及背架结构)、馈源支撑架及馈源仓对分析作用不大,为简便计算,可以等效为重力载荷均匀分布在俯仰组合上。各部分选用单元如表 1,图 5为所建立ANSYS模型图,该模型中Z轴为方位轴,指向天顶方向为正;Y轴为俯仰轴,收藏状态下向西为正;X轴根据Z轴、Y轴由右手定则确定[11, 12]。
| 天线构件 | Ansys选用单元 | 天线构件 | Ansys选用单元 |
| 座架 | BEAM 188 | 俯仰轴约束 | MPC 184 |
| 俯仰组合 | BEAM 188 | 俯仰电机约束 | COMBIN 14 |
| 注:(1)MPC184为多点约束单元,选择Revolute功能,可实现空间同一位置的两节点间抽象的链接,模拟轴孔间的旋转功能;(2)COMBIN14为弹簧-阻尼单元,俯仰电机位于座架上,通过小齿轮与俯仰大齿轮啮合,起固定和驱动反射体俯仰旋转功能,该分析中可用COMBIN14进行模拟计算。 | |||
|
| 图 5 50 m射电望远镜ANSYS有限元模型 Fig. 5 Our ANSYS finite-element model of the Miyun 50m radio telescope |
有限元模型边界条件的选取为:(1)座架滚轮处:Ux=Uy=ROTx=ROTy=ROTz=0,Uz取测量的轨道处水平差值;(2)方位中心枢轴:Ux=Uy=ROTx=ROTy=0;(3)俯仰轴处:采用销轴单元MPC184约束;(4)俯仰电机处:用弹簧-阻尼单元连接;(5)重力加速度载荷G,作用于模型整体;(6)主反射体及馈源部分等效重力载荷,作用于俯仰组合。其中,Ux、Uy、Uz分别是沿x、y、z方向的位移,ROTx、ROTy、ROTz分别是绕x、y、z方向的转角。
3.3 方位轴非线性倾斜偏差仿真分析天线的4组轮子之间互相间隔90°,在某一方位时4组轮子各处于不同水平高度的轨道面上。将测量的轨道水平度数据,按照测量方位每间隔90°依次选取4个(如方位角分别为0.9°、90.9°、180.9°、270.9°)数据为一组进行分组,共得到120组不同方位时天线4组滚轮的水平高度值。
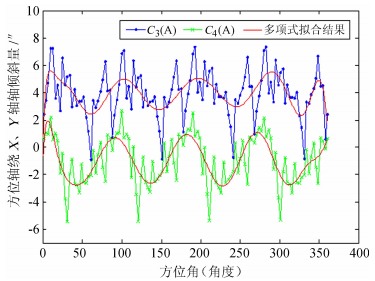
选取天线为收藏状态(即天线俯仰为90°),将每组水平值作为沿方位轴方向(Z向)的位移约束,依次代入模型座架底框正方向的4个顶点,进行ANSYS求解计算。仿真结果得到的天线方位轴绕X、Y轴的倾斜偏移量dA1、dE1随方位A的变化函数,如图 6。该函数关系显示,天线方位每旋转间隔90°,曲线总体上具有一个90°的周期,这正是由于每隔90° 4组滚轮又会到达同一组轨道位置处,因此其倾斜趋势相同。图示结果显示,方位轴绕X、Y轴倾斜偏差最大均超过7″。50 m天线对指向精度要求误差不超过19″,可见,轨道不平度引起的方位轴非线性倾斜已不容小觑。
|
| 图 6 方位轴绕X轴(上)、Y轴(下)倾斜偏差仿真结果 Fig. 6 Our simulation results of the deviations of the tilts of the azimuth axis of the antenna from the X and Y axes, respectively, for different azimuth values. In the plot, the results for the X axis are above those for the Y axis |
轨道不平度对天线的另一个影响是导致俯仰旋变产生测量误差。当天线沿着存在非均匀沉降和变形的轨道转动时,由于天线座架和俯仰反射体刚度不同,天线座架会出现不同程度的倾斜和微小变形,导致反射体部分与座架部分之间产生微小的相对转动,从而产生天线俯仰旋变测量误差。图 7显示了俯仰旋变误差的产生原理。

|
| 图 7 天线俯仰旋变测量器及其测量误差仿真模拟 Fig. 7 A picture of the instrument for measuring a pointing error of the azimuth axis of the antenna during antenna rotation (left-hand panel) and an illustration of measurement of the pointing error in our finite-element simulations (right-hand panel) |
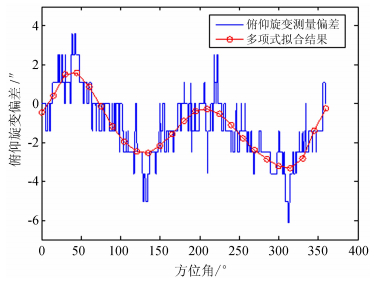
选择天线在非强烈日照且无风条件时,测量天线朝向天顶,方位旋转一周时的俯仰旋变偏差,测量结果如图 8,当天线方位角为45°、225°附近,即天线方位朝向西南及东北方向时,俯仰偏差较大,而方位朝向西北及东南方向时,俯仰偏差较小,最大值与最小值之差达到9″。
|
| 图 8 实测天线俯仰旋变偏差结果 Fig. 8 Our measured values of pointing errors of the azimuth axis of the antenna during antenna rotation |
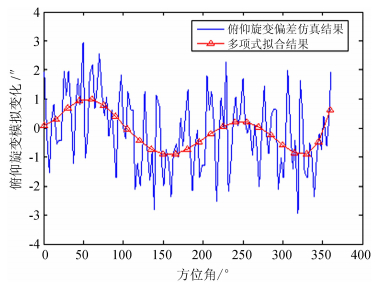
利用上一节中天线有限元模型仿真分析结果,可得到座架和反射体在位于俯仰轴同一位置处的不同两节点绕俯仰轴的旋转差ΔROTy,ΔROTy可以等效模拟为俯仰旋变定子和转子之间的相对转动,图 9为旋变偏差仿真结果。
|
| 图 9 仿真天线俯仰旋变偏差结果 Fig. 9 Our simulated values of pointing errors of the azimuth axis of the antenna during antenna rotation |
对比图 9与图 8发现,两者变化趋势相同,旋变偏差波谷和波峰出现的方位位置为同一位置,说明有限元仿真能比较真实地反映50 m天线的实际情况。天线旋转一周出现两个波峰、波谷说明座架的左右两个 “A” 字梁可能产生扭转。图 9的数据分布更为离散,且拟合平均值较小,可能是由于轨道水平值的测量误差以及有限元建模误差引起的,需进一步提高测量及模拟的精度。
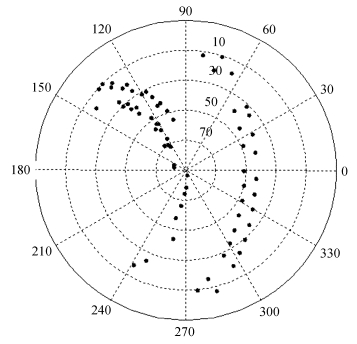
5 指向精度的误差校正 5.1 用扫描法获得指向校准实验数据在天线指向精度测量前,在X频段进行全天区指向观测和重新校准。所选射电源为3C273B、3C279、3C345、3C84和3C454.3等,射电源天区分布如图 10,测量的有效点数分别为方位66个,俯仰68个,运用天线控制软件引导天线跟上源、偏开方位、扫描、偏开俯仰、扫描,用扫描法进行方位及俯仰误差测量,获得有效数据样本。
|
| 图 10 指向校准天区分布 Fig. 10 The distribution of the sky directions pointed to by the antenna in our pointing-calibration experiment |
根据图 1修正流程图,一般的线性校正过程直接由实验测得的误差样本数据δA、δE进行系数C1~C8的辨识,然后再求得校正后的天线方位、俯仰残差分布;考虑轨道非线性误差的校正过程则先对原始误差样本进行非线性校正,然
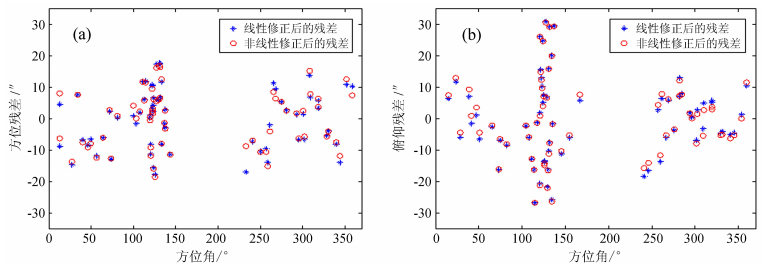
后再进行系数辨识及求残余误差均方差。两种指向校正后的天线指向剩余残差分布如图 11,由于轨道不平度较小,剩余残差变化不明显。
|
| 图 11 两种校正模型的残差分布对比. (a) 方位残差对比;(b) 俯仰残差对比 Fig. 11 Comparison of pointing-error residuals at various antenna azimuth angles resulting from the two pointing-calibration models. (a) Comparison for residuals in azimuths; (b) Comparison for residuals in altitudes |
两种模型的辨识系数结果如表 2,从表 2可以看出,考虑轨道不平度非线性误差修正模型C3、C4项分别比线性模型改变了3.776、-1.156 6,与图 6的模拟平均结果较为相似。两种校正方法最后的方位、俯仰、综合指向剩余残差均方差如表 3,其中A_ rms为方位指向误差均方差,H_ rms为俯仰
| 校正 模型 | 线性 模型 | 非线性 模型 | 校正 模型 | 线性 模型 | 非线性 模型 |
| C1 | 14.163 | 18.618 | C5 | 14.068 | 17.045 |
| C2 | 24.898 | 23.584 | C6 | 14.875 | 20.139 |
| C3 | -15.919 | -12.143 | C7 | 20.222 | 19.108 |
| C4 | -7.4661 | -8.6227 | C8 | -14.424 | -14.6 |
| 残差均 方差项 | 校正前 | 线性校 正模型 | 非线性校 正模型 | 结果 改善 |
| A_rms | 10.246 | 6.4910 | 5.5893 | 0.9017 |
| H_ rms | 28.685 | 12.8919 | 12.6781 | 0.2138 |
| AH_ rms | 30.46 | 14.4338 | 13.8555 | 0.5783 |
指向误差均方差,AH_ rms为综合指向误差均方差。对比线性校正模型结果,考虑轨道不平度非线性误差的指向校正方法将指向精度提高了0.578 3″,其中方位精度提高了0.901 7″,较为明显,俯仰精度提高了0.213 8″,对天线的指向精度有一定程度的改善。
6 结 论本文通过实验和有限元方法,探讨并提出了一种考虑轨道不平度的射电望远镜指向修正方法。通过对50 m天线进行相关研究,得出以下结论:
(1)测量了50 m天线的轨道不平度,轨道最高和最低处相差1.5 mm,已经超出全轨水平度不超过0.8 mm的要求;
(2)建立了50 m天线的有限元模型,通过有限元仿真计算了轨道不平度引起的方位轴非线性倾斜偏差,东西倾斜和南北倾斜最大均超过7″;
(3)仿真并实验测量了天线俯仰旋变测量偏差,仿真结果与测量结果具有一致性。天线旋转一周,俯仰旋变误差最大为±4″,旋变偏差直接影响天线的指向精度;
(4)对比线性修正模型,考虑轨道不平度的射电望远镜指向修正结果使得总的指向精度提高了约0.578 3″。
为进一步提高指向误差修正精度,还应努力提高水平度测量精度,增加测量点密度以更真实地反映实际轨道变形情况。同时应扩大观测射电源的样本容量,进行全天区的射电源观测。此外,影响天线指向精度非线性误差的因素多种多样,考虑除轨道不平度以外的其他因素对指向的影响,如温度、风载等,并建立相应的理论模型,也是今后研究的重点和探索方向。
| [1] | Levy R. Structural engineering of microwave antennas[M]. New York: IEEE Press, 1996. |
| [2] | Meeks M L, Ball J, Hull A, et al. The pointing calibration of the Haystack antenna[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(6): 746-751. |
| [3] | Vandenberg N R, Himwich W E. VLBI system documentation Mark IV field system[M]. America: NASA Goddard Space Flight Center, 1997. |
| [4] | Ott M, Witzel A, Quirenbach A, et al. An updated list of radio flux density calibrators[J]. Astronomy & Astrophysics, 1994, 284: 331-339. |
| [5] | Kong Deqing, Wang Songgen, Wang Jinqing, et al. A new calibration model for pointing a radio telescope that considers nonlinear errors in the azimuth axis[J]. Research in Astronomy and Astrophysics, 2014, 14(6): 733-740. |
| [6] | 张巨勇. 大型射电天线结构力学分析与误差研究[D]. 北京: 中国科学院国家天文台, 2006. |
| [7] | Zhang Xizhen, Zhu Xinying, et al. Measurements of Electronic Properties of the Miyun 50 m Radio Telescope[J]. Research in Astronomy and Astrophysics, 2009, 9(3): 367-376. |
| [8] | 高冠男, 汪敏, 施硕彪, 等. 云台40 m射电望远镜的指向误差校正[J]. 天文研究与技术——国家天文台台刊, 2007, 4(6): 188-194. Gao Guannan, Wang Min, Shi Shuobiao, et al. Pointing calibration for the 40m radio telescope in Yunnan Observatory[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2007, 4(6): 188-194. |
| [9] | 孔德庆, 施浒立, 张喜镇, 等. 射电望远镜指向误差的广义延拓插值修正方法[J]. 西安电子科技大学学报, 2008, 35(1): 157-161. Kong Deqing, Shi Huli, Zhang Xizhen, et al. Radio telescope pointing model based on the generalized extended interpolation correction method[J]. Journal of Xidian University, 2008, 35(1): 157-161. |
| [10] | 王松根. 大型射电天线轮轨接触分析与实验[D]. 杭州: 杭州电子科技大学, 2014. |
| [11] | 冯贞国, 郑元鹏. 50 m口径天线结构有限元模型的建立方法[J]. 无线电通讯技术, 2008, 34(3): 26-27. Feng Zhenguo, Zheng Yuanpeng. Establishment method of a finite element model of 50m antenna structure[J]. Radio Communications Technology, 2008, 34(3): 26-27. |
| [12] | 张亚林. 50 m口径射电望远镜天线结构静动力分析[J]. 电子机械工程, 2004, 20(6): 27-33. Zhang Yalin. The static and dynamic analysis of the 50m-diameter radio telescope antenna structure[J]. Electro-Mechanical Engineering, 2004, 20(6): 27-33. |



