相机在拍摄过程中通过感光芯片[1-2]来调节感光程度,因此当相机镜头正对光源而拍摄主体背对光源时,感光芯片感应到拍摄主体的反射光线较弱,感应到周围光源的反射光线较强[3]。成像后,图像的主体亮度较低,周围环境亮度较高。逆光条件得到的图像,主体部分较暗,且与周围环境形成强烈反差,因此难以获取该部分的有效信息,影响信息的提取。图 1中的四幅图片均在逆光环境下拍摄得到,观察发现逆光图像中的确存在高低对比明显的亮度差异,且主体亮度过低,会影响对其细节信息的有效快速识别。因此,恢复逆光图像很有必要。

|
图 1 逆光条件下拍摄图像 Figure 1 Photos taken in backlight condition |
恢复逆光图像应该有利于肉眼观测和计算机的快速准确识别。基于此,需要提升逆光图像低亮度区域的亮度,尽量保持高亮度区的亮度不变,整幅图片恢复后应该自然不失真。
在图像处理方面,已有很多研究者对改变图像亮度的方法进行了探究。文献[4]对交通图像进行了基于时间变化的自适应亮度调整,便于车辆检测和车牌识别;文献[5]对直方图与亮度的关系进行了探究,发现适于人眼观测的图像亮度直方图应该均匀分布;文献[6]通过直方图的均衡化来实现亮度调节;文献[7]和文献[8]对图像进行了亮度调节和小波变换融合,通过改变小波变化基来改变原图像的亮度,提升了图像的可读性;文献[9]对彩色图像进行了基于非线性Retinex反射模型的增强,改善了图像的局部对比度;文献[10]提出了一种基于同态滤波原理的井下光照不均图像的处理方法,抑制了低频分量,增强了高频分量;文献[11]对逆光图像的亮度进行了分段线性处理,并证明了在HSI空间处理亮度比直方图均衡法、同态滤波法和Retinex理论处理亮度都有效。在空间域对亮度进行处理的研究中,文献[12]采用对数函数的转换关系,在HSI空间模型下对图像的亮度进行调节,改善了图像画质;文献[13]利用自适应伽马校正模型对在HSI空间模型下的图像亮度进行调节,提高了对比度;文献[14]中分别采用了不同参数的幂函数形式在HSI空间模型中进行亮度调节,以降低光照不均对图片信息采集的影响。
从某种意义上讲,对逆光图像的恢复应该有利于肉眼观测和计算机的快速准确识别。为了能快速准确地处理逆光图像,本文借鉴文献[11-14]的思路,在空间域对亮度进行处理。
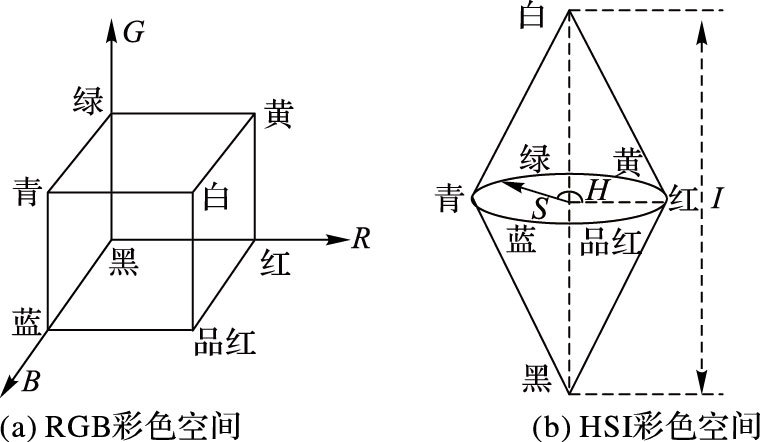
1 现有的亮度调节模型图像像素点的色彩可以用RGB彩色空间内的向量表示,如图 2(a);也可以用HSI彩色空间内的向量表示,如图 2(b)。HSI彩色空间的H代表色度(Hue),S代表饱和度(Saturation),I代表亮度(Intensity)。逆光情况对图像的亮度影响较大,而对图像的色度影响较小,而且在HSI模型中,亮度分量I与图像中彩色信息无关,可以单独处理,因此本文选择在HSI的模型中处理图像亮度。
|
图 2 彩色空间表示方式 Figure 2 Representations of color space |
图像中每个像素色彩从RGB到HSI模型转换公式[15]为:
| $H = \left\{ {\begin{array}{*{20}{r}} {\theta ,B \le G}\\ {360 - \theta ,B > G} \end{array}} \right.$ | (1) |
| $S = 1 - \frac{3}{{(R + G + B)}}[\min (R,G,B)]$ | (2) |
| $I = \frac{1}{3}(R + G + B)$ | (3) |
其中:假设R、G、B值已归一化到区间[0,1]内,则S、I的取值范围为[0,1],H的取值范围为[0,360) ,θ的取值如式(4) 。
| $\theta = \arccos \frac{{\frac{1}{2}[(R - G) + (R - B)]}}{{{{[{{(R - G)}^2} + (R - B)(G - B)]}^{\frac{1}{2}}}}}$ | (4) |
这种转换使得本文在后面的算法处理中可以单独对亮度分量I进行处理,大大简化了运算量。假设逆光图像中坐标为(x,y)处像素点归一化的亮度为fn(x,y),调节后的亮度为gn(x,y)。 fn(x,y)、gn(x,y)的取值范围都为[0,1](数值越大代表亮度越高),则逆光恢复处理过程可以看作将归一化后的图像亮度fn(x,y)经过一个变换函数Tr进行处理。即:
| ${g_n}\left( {x,y} \right) = Tr\left[ {{f_n}\left( {x,y} \right)} \right]$ | (5) |
为了方便叙述,在需要恢复的逆光图像中,本文将逆光条件下产生的亮度较低的区域称为逆光区域,光源较强的条件下产生的亮度较高的区域称为非逆光区域。对逆光图像进行恢复,需要提升逆光区域的亮度且尽量保证原始非逆光区域的亮度值。
1.1 分段线性调节| ${g_n}(x,y) = \left\{ \begin{array}{r} {k_1} \times {f_n}(x,y) + {b_1},{f_n}(x,y) \le \tau \\ {k_2} \times {f_n}(x,y) + {b_2},{f_n}(x,y) > \tau \end{array} \right.$ | (6) |
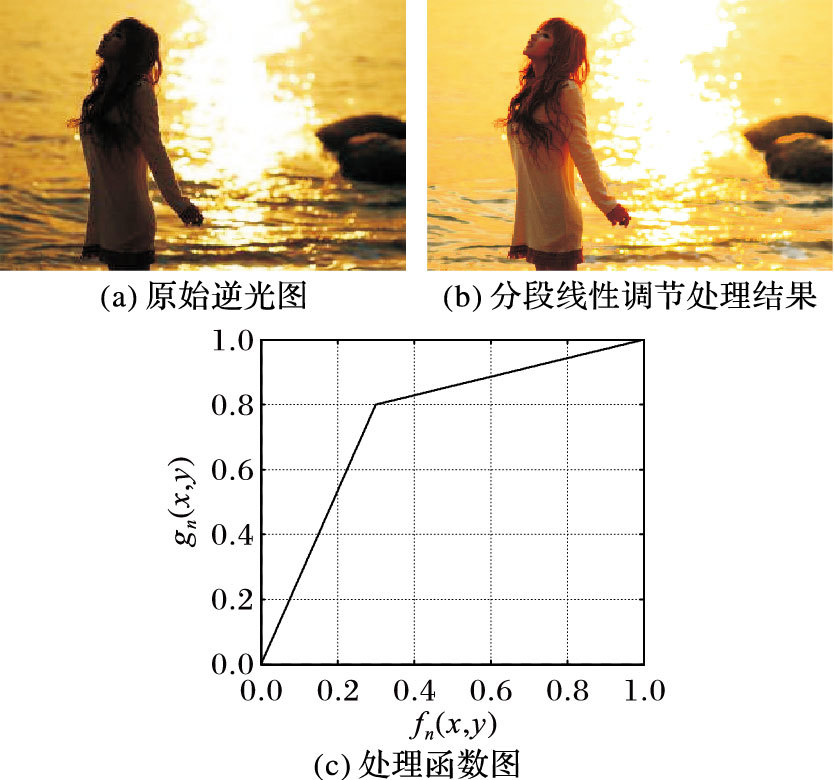
通过改变式(6) 中k1、k2、b1、b2和τ的值来改变亮度调节结果。当k1=8/3,k2=2/7,b1=0,b2=5/7,τ=0.3时,恢复结果如图 3所示。 由图 3可以看出,该分段模型虽然使逆光部分得到改善,但是处理效果不佳,且出现了明暗交接处失真的情况。失真情况是由函数分段处的不平滑造成的。若想在逆光部分得到较好的处理,非逆光部分的亮度就会提升得过高,这样也会造成失真。显然分段线性模型对逆光图像的处理并不能完全满足人们的需求。
|
图 3 分段线性调节结果对比 Figure 3 Results comparison of segmented linear adjustment |
文献[12]和文献[14]中分别采用了对数函数和不同参数的幂函数形式进行亮度调节。基于对逆光图像亮度处理的需求,选择对数函数[12]关系来改善对高亮度区的调节,公式为:
| ${g_n}(x,y) = C \times {\rm{lb}}[D \times {f_n}(x,y) + 1]$ | (7) |
为了方便叙述,称D为调节系数,用来改变变换函数的亮度提升性能。C的取值如下:
| $C = \frac{1}{{{\mathop{\rm l}\nolimits} {\rm{b}}(D + 1)}}$ | (8) |
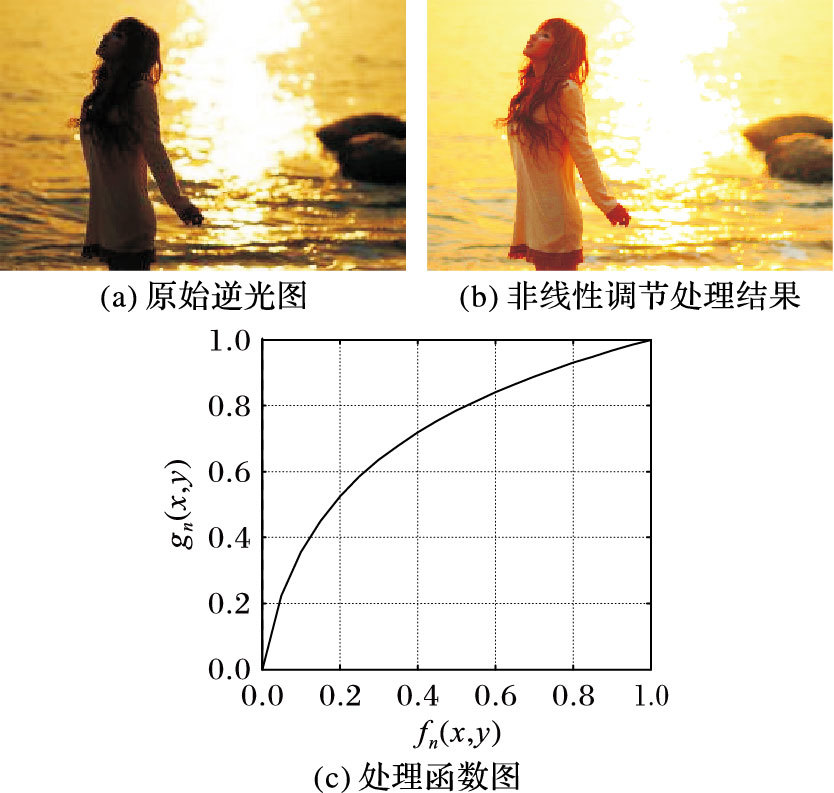
选择D=20,对图 1(a)进行逆光处理,结果如图 4所示,虽然处理效果比线性调节好了许多,但是高亮度区仍然存在失真情况。
|
图 4 非线性调节结果对比 Figure 4 Results comparison of nonlinear adjustment |
现有的对数亮度调节模型虽然都能够对逆光区域的亮度进行提升,但对非逆光区域的处理仍然不理想。因此本文提出一种改进方式,采取分段调节方式,对图像逆光区域进行自适应调节;对图像非逆光区域,在保证调节函数连续且逐渐收敛于直线gn(x,y)=fn(x,y)的情况下,选取合适的调节系数函数进行亮度调节。
2.1 分段阈值选取将图像的亮度区间分段为两段,分段阈值T∈[0,1]。令fn(x,y)≤T表示逆光区域,fn(x,y)>T表示非逆光区域。
T值的选取应该做到能有效区分逆光区域和非逆光区域,因此本文利用Otsu阈值分割方法[17]计算T,具体方法如下。设逆光图像大小为M×N像素,令{0,1/L,2/L,…,(L-1) /L}表示L个亮度级,ni表示亮度级为i的像素数,则图像像素总数MN=n0+n1+…+nL-1,令pi=ni/MN表示亮度级为i的像素占比,假设阈值T(0 <T<(L-1) /L)把图像亮度分为两类C1和C2(即逆光区域和非逆光区域),则阈值T为能够使类间方差σB2达到最大的值,即令下式达到最大值:
| $\sigma _B^2(T) = \frac{{{{[{m_I}{P_1}(T) - m(T)]}^2}}}{{{P_1}(T)[1 - {P_1}(T)]}}$ | (9) |
式中:P1(T)为像素被分到C1的概率,m(T)为直至T级的亮度累加均值,mI为整个图像的平均亮度。
| ${P_1}(T) = \sum\limits_{i = 0}^T {{p_i}} $ | (10) |
| $m(T) = \sum\limits_{i = 0}^T {i{p_i}} $ | (11) |
| ${m_I} = \sum\limits_{i = 0}^{L - 1} {i{p_i}} $ | (12) |
在用对数函数进行调节时,单纯地将D选取为某一正实数虽然能够对部分逆光图像得到较好的恢复效果,但是对整体较暗的图像恢复程度差;且当fn(x,y)较大时,仍然有较大的亮度提升,这是不希望得到的。因此本文选取分段函数作为变换函数:
| ${g_n}(x,y) = \left\{ \begin{array}{r} {C_1} \times {\mathop{\rm l}\nolimits} {\rm{b[}}{D_1} \times {f_n}(x,y) + 1],{f_n}(x,y) \le T\\ {C_2} \times {\mathop{\rm l}\nolimits} {\rm{b}}[{D_2} \times {f_n}(x,y) + 1],{f_n}(x,y) > T \end{array} \right.$ | (13) |
| ${C_i} = \frac{1}{{{\mathop{\rm l}\nolimits} {\rm{b}}({D_i} + 1)}};i = 1,2$ | (14) |
式中:分段阈值T由Otsu阈值分割方法计算得到。 Di(i=1,2) 为第i段的调节系数,当fn(x,y)≤T时,选择D1作为调节系数;当fn(x,y)>T时,选择D2作为调节系数。 本文希望得到这样的调节系数:Di是fn(x,y)的连续函数;当fn(x,y)≤T,D1值较大,当fn(x,y)≤T,D2值逐渐变小,且变换函数逐渐收敛于直线gn(x,y)=fn(x,y),即尽量维持高亮度区域的亮度原值。 基于以上要求,Di的选取采用如下公式:
| ${D_i} = \left\{ \begin{array}{r} A,{f_n}(x,y) \le T,i = 1\\ \frac{{T \times A - T}}{{(1 - T){f_n}(x,y)}} - \frac{{T \times A - 1}}{{1 - T}},{f_n}(x,y) > T,i = 2 \end{array} \right.$ | (15) |
其中:A为某一正实数,A越大,fn(x,y)≤T部分的亮度提升幅度越高。通过多次实验发现,A值并非越大越好,因为A值过大会导致逆光区域由于亮度过分提高而产生严重的图像失真。本文希望:当逆光区域面积较大而非逆光区域面积较小时,fn(x,y)≤T部分得到较高的亮度提升;而当逆光区域面积较小而非逆光区域面积较大时,fn(x,y)≤T部分得到较小的亮度提升。基于此,A的选取采用如下公式:
| $A = k \times \sqrt {\frac{{{n_{[{f_n}(x,y) \le T]}}}}{{MN - {n_{[{f_n}(x,y) \le T]}}}}} $ | (16) |
其中:k为某一正常数,取k=50;n[fn(x,y)≤T]表示fn(x,y)≤T的像素个数。
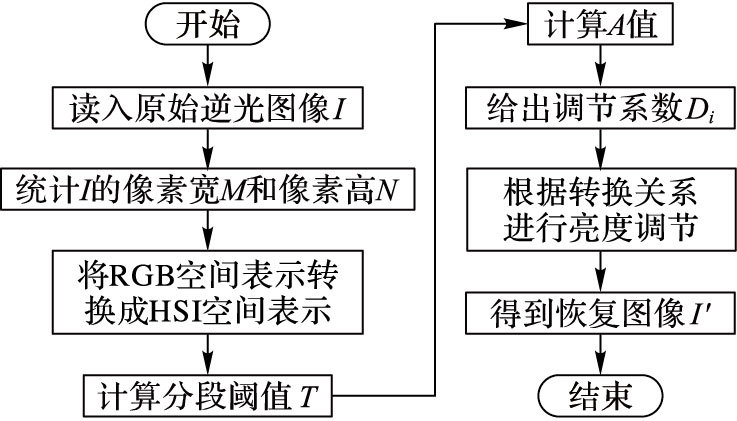
基于上述原理,图像恢复的过程如图 5所示。
|
图 5 本文算法流程 Figure 5 Flow of the proposed algorithm |
本文所提出的改进算法在内存为8 GB(型号为DDR RME510H38C6T- 400) 、CPU频率为3.2 GHz、操作系统为64位Windows 7的计算机上运行。图 6给出了原始逆光图像、本文改进算法所得处理结果和文献[12]的处理结果。

|
图 6 两种方法恢复结果对比 Figure 6 Comparison of recovery results by two methods |
利用本文的改进方法,可以有效恢复原始图像中亮度较低部分的细节,并且与文献[12]的传统非线性逆光处理方法相比,本文改进方法对原始图像的高亮度部分改动较小,没有产生失真。图像1中女生的头发和衣服由于逆光原因难以辨别,本文改进方法结果图中能够明显分辨出女生的头发和裙子颜色,与文献[12]的传统方法结果相比,本文方法能够保持原始图像中的高亮区域,而文献[12]方法的结果中由于海面亮度过高而产生了失真;图像2中弹琴女孩的肤色和耳环难以辨别,本文改进方法结果图中能够明显分辨出女孩的肤色和耳环,与文献[12]的传统方法结果相比,本文方法能够保持原始图像中的高亮区域,而文献[12]方法的结果中门外部分亮度由于过高而丢失了部分细节信息;图像3中三个人以及图片左半部分的门内的人物难以辨别,本文改进方法结果图中能够明显分辨出人物,与文献[12]的传统方法结果相比,本文方法能够保持原始图像中的高亮区域,而文献[12]方法的结果中右上角的亮度由于过高而丢失了树枝的细节;图像4中车头和树木由于逆光原因难以辨别,本文改进方法结果图中能够明显分辨出车头颜色和树木颜色等逆光部分的细节,与文献[12]的传统方法结果相比,本文方法能够保持原始图像中的高亮区域,而文献[12]方法的结果中天空的亮度由于过高而丢失了部分电线的信息;图像5中路灯和绿树由于逆光原因难以辨别,本文改进方法结果图中能够明显分辨出绿树颜色和路灯,与文献[12]的传统方法结果相比,本文方法能够恢复原始路灯和车辆颜色并保持原始图像中的高亮区域,而文献[12]方法的结果中由于提高了对比度导致失真。
3.2 恢复效果判断准则为了更好地对比逆光图像的非线性亮度调节方法,本文对调节时长和调节后的亮度比例进行了统计,并将本文改进方法和文献[12]的方法在时效性和处理效果上进行了对比,结果如表 1、2所示。从表中数据可以看出,虽然本文所提出的改进方法在处理时间上略长于文献[12]的方法,但本文所提出的改进方法对高亮度区域的像素改动较少,而文献[12]在提升亮度的同时,对高亮度区域的改动较大。因此可以说本文的改进方法时效性虽然一般,但处理效果较好。
从表 1还可以看出,处理的运行时间与图像的大小,即像素值(M×N)直接相关,M×N越大,处理时间越长。改进方法在处理速度上要慢于文献[12]的传统方法,这主要是由于改进的方法是对亮度进行分段非线性调节,而非整体非线性调节,但总的来说,运行效率较高,处理速度尚可,而这主要因为本文仅选择用HSI模型的I分量来进行逆光处理,而不是用RGB模型的三个颜色分量来处理。
| 表 1 两种方法处理时长统计 Table 1 Statistics of processing time for two methods |
从表 2中可以看出,在原逆光图像中有一个普遍存在的现象:背景和主体的亮度相差比较多,背景主要在高亮度(0.7~1) 范围内,而主体主要在低亮度(0~0.3) 范围内,0.3~0.7这个中间亮度范围内,基本上没有像素。逆光处理主要是将低亮度区域的像素通过非线性变换转移到中亮度区域,从处理过的数据中,本文也可以证实这一点。从表中可以看出,在0.7~1区间,改进方法结果图的像素所占比例比传统方法结果图的像素所占比例更接近原始图,改进的方法对图像像素亮度的调节主要是将0~0.3部分调节至0.3~0.7部分,而对高亮度区(0.7~1) 改动较少,而文献[12]的传统方法在高亮度区的改动较大。除此之外,亮度分布越均匀,范围越广,图片的质量理论上越好,这点从处理图的数据中也可以发现,本文的处理有利于更好地分辨细节。
| 表 2 两种方法处理前后亮度值域对比 Table 2 Comparison of bcenterness value before and after treatment |
为了改善逆光图像,使之能够更好地被肉眼观测和计算机识别,本文提出了一种对非线性亮度提升模型的改进方式。通过Otsu阈值分割方法得到分段阈值T,通过计算逆光区域像素占总像素的比值得到非逆光区域的亮度提升系数,通过分段的方式对逆光图像亮度进行处理。经过处理,恢复后的图像能够明显得到原逆光区域的细节信息。
| [1] | 甘波, 魏廷存, 郑然. CMOS图像传感器芯片的自动白平衡算法[J]. 液晶与显示, 2011, 26 (2) : 224-228. ( GAN B, WEI T C, ZHENG R. Automatic white balance algorithm for CMOS image sensor chip[J]. Chinese Journal of Liquid Crystals and Displays, 2011, 26 (2) : 224-228. doi: 10.3788/YJYXS ) |
| [2] | 郭惠楠.彩色数字相机成像系统的关键性技术研究[D].西安:西安光学精密机械研究所,2014:18-22. ( GUO H N. Research on the key technology of color digital camera imaging system[D]. Xi'an:Xi'an Institute of Optics and Fine Mechanics, 2014:18-22. ) |
| [3] | 陈参宁, 邓华秋, 王剑华. 基于光圈控制的自动曝光算法研究[J]. 传感器与微系统, 2011, 30 (11) : 46-48. ( CHEN C N, DENG H Q, WANG J H. Research on automatic exposure algorithm based on iris control[J]. Transducer and Microsystem Technologies, 2011, 30 (11) : 46-48. ) |
| [4] | 刘操, 郑宏, 黎曦. 基于自适应亮度基准漂移的十字路口交通图像增强处理研究[J]. 武汉大学学报(信息科学版), 2015, 40 (10) : 1381-1385. ( LIU C, ZHENG H, LI X. Traffic image enhancement processing based on adaptive luminance reference drift[J]. Geomatics and Information Science of Wuhan University, 2015, 40 (10) : 1381-1385. ) |
| [5] | GRAHAM D, SCHWARZ B, CHATTERJEE A, et al. Preference for luminance histogram regularities in natural scenes[J]. Vision Research, 2016, 120 : 11-21. doi: 10.1016/j.visres.2015.03.018 |
| [6] | SANTHI K, WAHIDA B R S D. Contrast enhancement using brightness preserving histogram plateau limit technique[J]. International Journal of Engineering and Technology, 2014, 6 (3) : 1447-1453. |
| [7] | 杨俊, 赵忠明. 基于IHS变换和亮度调节的遥感图像融合方法[J]. 计算机应用研究, 2007, 24 (4) : 195-197. ( YANG J, ZHAO Z M. Research on remote sensing image fusion method based on IHS transform and brightness adjustment[J]. Application Research of Computers, 2007, 24 (4) : 195-197. ) |
| [8] | ZHANG H. A novel enhancement algorithm for low-illumination images[C]//CISP 2013:Proceedings of the 6th International Congress on Image and Signal Processing. Piscataway, NJ:IEEE, 2013:240-244. |
| [9] | 张雪峰, 赵莉. 基于改进Retinex的图像增强算法[J]. 南京理工大学学报(自然科学版), 2016, 40 (1) : 24-28. ( ZHANG X F, ZHAO L. Image enhancement algorithm based on improved Retinex[J]. Journal of Nanjing University of Science and Technology, 2016, 40 (1) : 24-28. ) |
| [10] | 刘毅, 贾旭芬, 田子建. 一种基于同态滤波原理的井下光照不均图像处理方法[J]. 工矿自动化, 2013, 39 (1) : 9-12. ( LIU Y, JIA X F, TIAN Z J. A processing method for underground image of uneven illumination based on homomorphic filtering theory[J]. Industry and Mine Automation, 2013, 39 (1) : 9-12. ) |
| [11] | KANG G-Y, HUANG J-W, LI D-H, et al. A novel algorithm for uneven illumination image enhancement[C]//IMCCC 2012:Proceedings of the Second International Conference on Instrumentation, Measurement Computer Communication and Control. Washington, DC:IEEE Computer Society, 2012:831-833. |
| [12] | WANG S, ZHENG J, HU H-M. Naturalness preserved enhancement algorithm for nonuniform illumination images[J]. IEEE Transactions on Image Processing, 2013, 22 (9) : 3538-3548. doi: 10.1109/TIP.2013.2261309 |
| [13] | SHIN Y, JEONG S, LEE S. Efficient naturalness restoration for nonuniform illumination images[J]. IET Image Processing, 2015, 9 (8) : 662-671. doi: 10.1049/iet-ipr.2014.0437 |
| [14] | YUN H J, WU Z Y, WANG G J, et al. A novel enhancement algorithm combined with improved fuzzy set theory for low illumination images[J]. Mathematical Problems in Engineering, 2016 (8) : 1-9. |
| [15] | GONZALEZ R C. Digital Image Processing[M]. New Jersey: Pearson Prentice Hall, 2008 : 257 -262. |
| [16] | 高彦平.图像增强方法的研究与实现[D].武汉:华中科技大学,2008:12-28. ( GAO Y P. Research and implementation of image enhancement method[D]. Wuhan:Huazhong University of Science and Technology, 2008:12-28. ) |
| [17] | SUSRAMA I G, PURNAMA K E, PURNOMO M H. Automated analysis of human sperm number and concentration (oligospermia) using Otsu threshold method and labelling[J]. IOP Conference Series:Materials Science and Engineering, 2016, 105 (1) : 12038-12048. |




