扩展功能
文章信息
- 韦德智, 葛淼, 温国涛, 王聪霞
- WEI Dezhi, GE Miao, WEN Guotao, WANG Congxia
- 地理环境与健康人血尿素氮参考值的关系
- Relationship between geographic environment and blood urea nitrogen reference values of healthy people
- 吉林大学学报(医学版), 2017, 43(03): 600-606
- Journal of Jilin University (Medicine Edition), 2017, 43(03): 600-606
- 10.13481/j.1671-587x.20170326
-
文章历史
- 收稿日期: 2016-10-10
2. 地理学国家级实验教学示范中心(陕西师范大学), 陕西 西安 710119;
3. 西安交通大学医学院第二附属医院心内科, 陕西 西安 710004
2. National Demonstration Center for Experimental Geography Education(Shaanxi Normal University), Xi'an 710119, China;
3. Department of Cardiovascular Medicine, Second Affiliated Hospital, Medical School of Xi'an Jiaotong University, Xi'an 710004, China
尿素氮(urea nitrogen, UN)是血浆蛋白氮以外的含氮化合物的一种,为人体蛋白质代谢的主要终末产物。血尿素氮(blood urea nitrogen,BUN)是目前健康体检的必检项目之一,也是临床上最广泛应用于肾功能评估的血清标志物之一,其在心功能等方面的评估中也起一定作用。BUN水平在诊断肾脏疾病、判断药物性肾脏损伤、预测急性心力衰竭的心血管事件和评估急性心肌梗死患者预后效果等方面起重要的指示作用[1-2]。
目前,国内外尚无关于地理环境与BUN参考值关系的相关报道。国内外学者对医学参考值影响因素的研究多关注于年龄、性别和身高等方面而未考虑到地理环境对医学参考值的影响。为探讨健康人BUN参考值的地理分布规律,并为制订不同地理条件下健康人BUN参考值的标准提供科学依据,本研究观察健康人BUN参考值与地理环境之间的关系,根据二者关系建立了预测模型[3],并构建了中国健康人BUN参考值地理分布图。
1 资料与方法 1.1 BUN参考值资料检索中国期刊网全文数据库、超星数字图书馆、中国生物医学文献数据库、中国科学引文数据库、万方全文期刊数据库等相关网络数据库,获取中国403个省、市、县级医疗单位和相关科研机构测定的33 521名健康人BUN参考值,测定人群的年龄为18~89岁。样本点分布在中国23个省、4个直辖市、5个自治区,缺乏香港、澳门和台湾地区的资料,东部地区的资料多于西部地区(图 1)。所选取的BUN实测数据均来自健康人群,排除标准:原发性高血压疾病史患者、心肝肾等主要脏器功能障碍患者、严重(急、慢性)感染患者、6个月内有创伤或进行手术者和服用肾功能损伤药物患者等。所有受测者均在检查前禁食10 h,于次日早晨对血样标本进行采集,在采集后及时送检。检测仪器为日立全自动生化分析仪,检测方法为酶偶联速率法[4-5]。
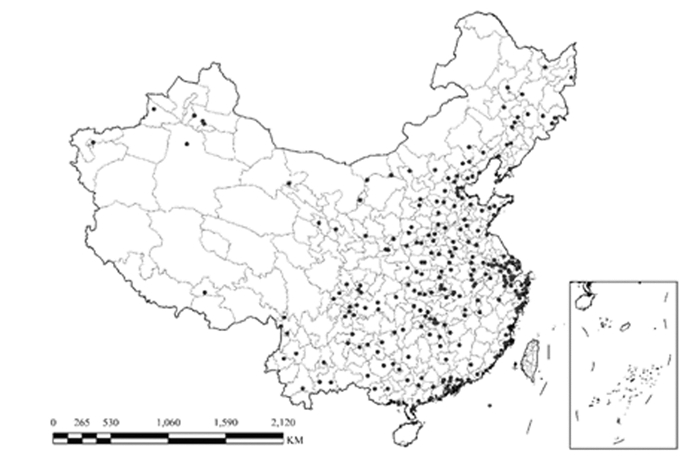
|
| 图 1 健康人BUN参考值样本点分布图 Figure 1 Sample distribution map of BUN reference values of healthy people |
|
|
选取4类与人体健康紧密相关的地理环境指标,分别为地理位置指标、地势指标、气候指标和土壤指标,前两者数据来自国家测绘局数据中心共享资料、后两者数据分别来自中国气象数据共享服务网和世界土壤数据库。地理位置指标主要包括经度(°, X1)和纬度(°, X2),地势指标主要为海拔(m, X3),气候指标包括年日照时数(h, X4)、年平均气温(℃, X5)、年平均相对湿度(%, X6)、年降水量(mm, X7)、气温年较差(℃, X8)和年平均风速(m·s-1, X9),土壤指标包括表土砂砾百分率(%, X10)、表土粉粒百分率(%, X11)、表土黏粒百分率(%, X12)、表土参考容量(kg·dm-3, X13)、表土容重(kg·dm-3, X14)、表土石砾含量(% vol, X15)、表土有机质含量(% wt, X16)、表土pH值(X17)、表土(粘土)阳离子交换量(cmol·kg-1, X18)、表土(粉土)阳离子交换量(cmol·kg-1, X19)、表土基本饱和度(%, X20)、表土总可交换量(cmol·kg-1, X21)、表土碱度(cmol·kg-1, X22)和表土盐分(ds·m-1, X23)。从数据库获取数据后,将各项指标与样本点进行匹配。
1.3 资料分析方法 1.3.1 空间自相关分析空间自相关是指同一个变量在不同空间位置上的相关性,是空间单元属性值聚集程度的一种度量[6]。为了检验所采集的样本数据是否存在空间相关性,采用ArcGIS 10.1软件将样本数据进行全局空间自相关检验,进而确定地理因素对健康人BUN参考值是否存在不可忽视的影响。
1.3.2 相关分析相关分析研究现象之间是否存在某种依存关系,并对具体有依存关系的现象探讨其相关方向以及相关程度,其是研究随机变量之间相关关系的一种统计方法[7]。采用SPSS 22.0统计软件建立数据库,通过双变量相关分析确定中国健康人BUN参考值与地理因素的相关性,并提取与中国健康人BUN参考值显著相关的地理因素。
1.3.3 线性回归分析线性回归分析是研究一个因变量与一个或多个自变量之间线性关系的统计方法[8]。采用SPSS 22.0统计软件对健康人BUN参考值与其相关性显著的地理因素进行线性回归分析,根据结果中的回归系数及膨胀系数确定运用普通最小二乘法的多元线性回归方程是否可靠,若可靠则采用该模型计算全国各地健康人BUN参考预测值,若不可靠则舍弃该模型。
1.3.4 主成分分析主成分分析是利用降维的思想将多个变量通过线性变化以选出较少个数重要变量的一种多元统计分析方法。其是将原本较多的具有一定相关性的变量重新组合成一组新的且互相无关的综合指标来代替原来的指标,可以很好地解决共线性问题[9]。地理环境是由多种要素共同组成的综合体,其各要素之间存在着复杂的关系,为了使地理因素的关系变得清晰,采用SPSS 22.0统计软件通过主成分分析得出一个回归模型并用该模型对全国各地区的健康人BUN参考值做出预测[10]。
1.3.5 岭回归分析岭回归分析是一种有偏估计回归方法,其目的是解决共线性数据问题,其可以克服回归自变量内部自身强的线性关系对回归系数的最小二乘估计量的影响[11]。采用SAS软件建立岭回归模型并利用该模型预测出全国各地的健康人BUN参考值。
1.3.6 配对样本t检验配对样本t检验过程可以检验两个相关的样本是否来自具有相同均值的总体[12]。采用SPSS 22.0统计软件对各模型预测值与实测值进行配对样本t检验,根据检验结果的t值与P值判定各模型预测值和实测值的拟合度以确定最优模型。
1.3.7 地统计分析地统计分析以区域化变量为基础,借助变异函数,是研究既有随机性又有结构性或空间相关性和依赖性的自然现象的一门科学。地统计分析的特点是既考虑到样本值的大小,又重视样本空间位置及样本间的距离,弥补了经典统计学忽略空间位置的缺陷[6]。地统计分析首先将样本数据进行Kolmogorov-Smirnov(K-S)正态分布概率检验法,验证数据正态性,根据数据的正态性,确定插值方法后对数据进行变异分析,进一步探讨空间相关性以及选择最适宜的插值模型[13],并采用该模型插值构建中国健康人BUN参考值的地理空间分布图,以便直观地反映出中国健康人BUN参考值的分布规律。
2 结果 2.1 空间自相关分析Moran’s I指数为正,且大于0,全局自相关系数Z值为18.173 644,大于0.01的置信水平值为2.58,P值为0.000 00,整个结果呈现出BUN参考值数据有很强的空间自相关性。见图 2(封三)。
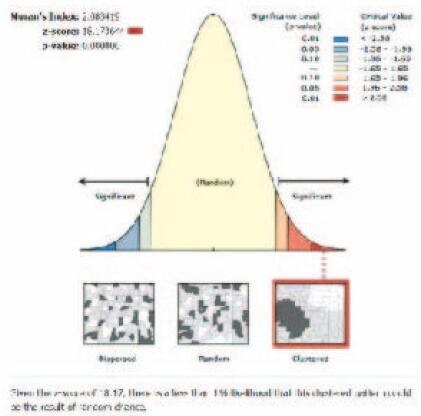
|
| 图 2 BUN参考值空间自相关分析图 Figure 2 Diagram of spatial autocorrelation analysis of BUN reference values |
|
|
以健康人BUN参考值作为因变量,23项地理因素数据作为自变量进行相关分析,可得到健康人BUN参考值与各项地理因素之间的单相关系数(r)和P值。
23项地理因素中有5项与健康人BUN参考值存在相关性,包括纬度(X2)、海拔(X3)、年平均气温(X5)、年平均相对湿度(X6)和年降水量(X7)。其中,纬度、海拔与健康人BUN参考值呈正相关关系,年平均气温、年平均相对湿度和年降水量与健康人BUN参考值呈负相关关系。见表 1。
| Geographic factor | r | P |
| Longitude(X1) | 0.019 | 0.719 |
| Latitude(X2) | 0.141 | 0.008 |
| Altitude(X3) | 0.144 | 0.007 |
| Annual sunshine duration(X4) | 0.087 | 0.102 |
| Annual mean temperature(X5) | -0.129 | 0.016 |
| Annual mean relative humidity(X6) | -0.157 | 0.003 |
| Annual precipitation(X7) | -0.132 | 0.013 |
| Annual temperature range(X8) | 0.089 | 0.095 |
| Annual mean wind speed(X9) | -0.022 | 0.686 |
| Percentage of topsoil gravel(X10) | 0.046 | 0.389 |
| Percentage of topsoil silt(X11) | 0.011 | 0.836 |
| Percentage of topsoil clay(X12) | -0.046 | 0.390 |
| Topsoil reference capacity(X13) | 0.060 | 0.261 |
| Topsoil capacity(X14) | 0.051 | 0.337 |
| Topsoil gravel content(X15) | -0.046 | 0.389 |
| Topsoil organic content(X16) | -0.075 | 0.158 |
| Topsoil PH(X17) | 0.017 | 0.755 |
| Topsoil(clay) cation exchange capacity(X18) | 0.101 | 0.059 |
| Topsoil(sit) cation exchange capacity(X19) | 0.034 | 0.526 |
| Topsoil basic saturation(X20) | 0.027 | 0.609 |
| Topsoil total exchange capacity(X21) | —0.011 | 0.832 |
| Topsoil alkalinity(X22) | 0.102 | 0.055 |
| Topsoil salinity(X23) | 0.001 | 0.989 |
以健康人BUN参考值为因变量,与之相关的5项地理因素为自变量建立多元线性回归方程。方程的F检验结果为:F=2.903,P=0.014,说明回归方程具有很强的显著性;在回归系数的显著性检验中,仅X3的显著性水平小于0.05,其余4项自变量的回归系数均大于0.05,这表明共线性问题可能存在于各变量之间,各变量膨胀系数(VIF)诊断结果显示:VIF2=21.66,VIF3=3.644, VIF5=14.04,VIF6=3.691,VIF7=6.150,其中有2个膨胀系数均大于10,即该5个自变量之间存在多重共线性问题,作为普通最小二乘法的多元线性回归模型可能会与事实情况不符,因此选择放弃该模型。
2.4 主成分分析 2.4.1 因子分析适用性判断在进行主成分分析之前需要对各变量进行因子分析。采用SPSS 22.0统计软件中的因子分析模块,可知5项与健康人BUN参考值呈显著相关的地理因素指标的KMO适度抽样值为0.611,Bartlett’s球形度检验Sig值为0.000(小于极显著水平0.01),因此拒绝原假设,可认为各变量之间存在相关关系,适合做因子分析,可以进行主成分提取。
2.4.2 主成分提取将与健康人BUN参考值呈显著相关的5项地理因素数据进行标准化处理,计算初始特征值、贡献率,按照一定的原则进行主成分提取。第1个主成分的初始特征值为3.608,累积贡献率为72.164%<80%,而第2个主成分的初始特征值为0.931, 较接近1, 其解释了5个原始变量总方差的18.617%, 因此选取前2个主成分代替原有的5个初始变量。见表 2。
| Component | Initial eigenvalue | Extraction sum of squared loadings | |||||
| Total | Percentage of variance(η/%) | Cumulative percentage(η/%) | Total | Percentage of variance(η/%) | Cumulative percentage(η/%) | ||
| 2 | 3.608 | 72.164 | 72.164 | 3.608 | 72.164 | 72.164 | |
| 3 | 0.931 | 18.617 | 90.781 | 0.931 | 18.617 | 90.781 | |
| 5 | 0.282 | 5.632 | 96.413 | ||||
| 6 | 0.153 | 3.057 | 99.470 | ||||
| 7 | 0.026 | 0.530 | 100.000 | ||||
根据主成分特征向量值,得到所提取的2个主成分的表达式:Z1=-0.482 2X2-0.233 2X3+0.494 3X5+0.472 7X6+0.494 3X7;Z2=-0.370 0X2+0.923 4X3+0.037 31X5-0.045 60X6+0.083 95X7。
以主成分Z1和Z2作为自变量,健康人BUN参考值作为因变量进行回归分析,得到以下回归方程:Ŷ=5.112-0.002 866Z1+0.00002977Z2+0.5310;将主成分Z1和Z2的表达式代入上述回归方程,可得到健康人BUN参考值与5项地理因素指标的线性回归方程:Ŷ=5.112-0.0001271X2+0.00009461X3-0.0001405X5-0.0001366X6-0.0001391X7±0.5311;其中,Ŷ是健康人BUN参考值, 0.5310是剩余标准差的值。
2.5 岭回归分析采用SAS软件,以健康人BUN参考值为因变量和与之相关的5项地理指标为自变量进行岭回归分析,建立岭迹图,其中横轴为岭参数K、纵轴为各项地理因素回归系数(图 3,见封三)。各地理因素在K=0.2时逐渐趋于稳定,因此考虑选取岭参数为0.2。根据SAS软件进行程序编程运算结果得到健康人BUN参考值与5项地理因素之间的回归方程Ŷ=4.885 1+0.006200X2+ 0.00009000X3-0.0044000X6-0.00003000X7 ±0.5323。其中,Ŷ是健康人BUN参考值,0.532 3是剩余标准差的值。
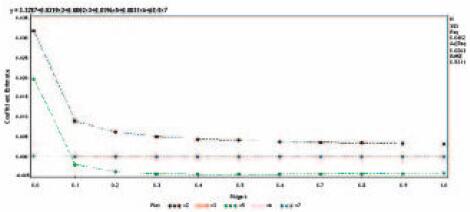
|
| 图 3 BUN参考值岭迹图 Figure 3 Ridge trace figure of BUN reference values |
|
|
根据主成分分析和岭回归分析所得到的2个预测模型,分别计算出样本点健康人BUN参考值的预测值,对预测值和实测值进行配对样本t检验,结果显示:2个预测模型的配对样本检验显著性均大于0.05,说明2个预测模型的预测值与实测值的拟合度比较理想,但2个预测模型不能相互替代。因此,本研究选取配对样本检验显著性更优的主成分分析预测模型为健康人BUN参考值的最优预测模型,其回归方程:Ŷ=5.112+ 0.0001271X2+ 0.00009461X3-0.0001405X5-0.0001368X6-0.000 139 1X7 ±0.5310;其中,Ŷ是健康人BUN参考值,0.531 0是剩余标准差的值。见表 3。
| Predicted model | Standard deviation | Average of standard error | t | P |
| Principal component | 0.529 | 0.028 | 0.023 | 0.982 |
| Ridge regression | 0.528 | 0.028 | -0.106 | 0.916 |
采用最优预测模型预测出全国2 322个市县地区的健康人BUN参考值,在SPSS 22.0统计软件中进行K-S检验(Z=29.38,P=0.000),说明预测数据不服从正态分布,因此空间插值方法选用析取克里金法。采用Arc GIS软件对预测数据进行趋势分析,可得到中国健康人BUN参考值空间变化趋势图(图 4,见封三),该图可见中国健康人BUN参考值在X轴和Y轴上的变化均不是简单线性的,而呈现的是二阶变化,因此在进行插值之前还需将数据进行二阶变换处理。
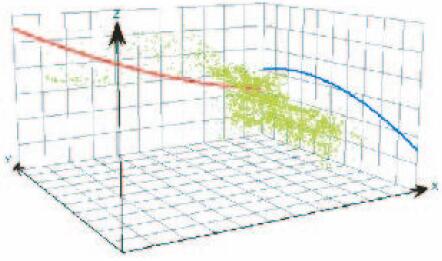
|
| 图 4 BUN参考值空间变化趋势图 Figure 4 Spatial trends diagram of BUN reference values |
|
|
在进行上述处理之后,采用Arc GIS软件中的地统计模块,选取析取克里金法进行插值,在已矢量化的地图上精准定位2 322个市县进行插值,最终输出中国健康人BUN参考值地理分布图(图 5,见封三)。图中不同颜色代表不同的BUN参考值,色调相近说明区域间BUN参考值相近,反之BUN参考值差异大。
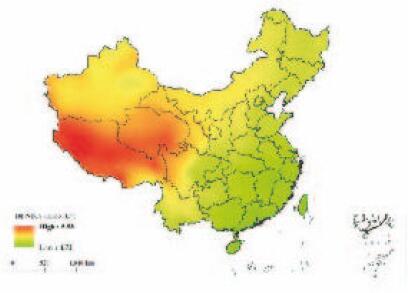
|
| 图 5 BUN预测参考值分布图 Figure 5 Distribution map of predicted values of BUN |
|
|
空间自相关分析结果显示:Moran指数为正,说明中国健康人BUN的分布与空间信息呈正相关关系,即空间分布聚集度大的地方,BUN参考值也相应大。空间自相关的显著性P值为0.000,说明地理环境与BUN参考值之间存在着很强的相关性,二者并不是相互独立的。中国健康人BUN参考值会随着空间属性的差异而不同,因此对地理环境与BUN参考值进行关系分析是可行的,空间自相关分析后的各处理流程均有意义。
相关分析结果显示:中国健康人BUN参考值与5项地理因素存在相关关系,其中与纬度、海拔、年平均相对湿度呈极显著相关关系,纬度与中国健康人BUN参考值呈正相关关系,这与空间自相关分析的结果呈现了良好的一致性。
在模型构建过程中,经过共线性诊断发现各地理因素存在多重共线性问题,说明BUN参考值与地理因素之间存在着复杂的非线性关系。在这种情况下多元线性回归模型不合理,而主成分分析和岭回归分析均能很好地解决共线性问题,避免了模型失效的问题[14]。经模型构建、最优模型选取、预测及插值出图后,中国健康人BUN参考值的空间分布规律为东部较低,西部较高,随海拔呈较有规律的波动,东南部沿海地区及东北平原地区BUN参考值相对较低,青海地区和西藏地区则相对较高。海拔作为最重要的相关因素,在预测值分布图上的体现非常明显。BUN预测参考值分布图显示:BUN参考值的分布基本贴合我国地形三大阶梯,随着海拔高度的升高,BUN参考值逐渐升高,这与相关分析中BUN参考值与海拔高度呈正相关关系的结果一致。
肾脏是人体极为重要的排泄器官,其在保持机体内环境的稳定、维持人体新陈代谢等方面起关键作用。当肾脏发生功能性障碍时,体内的代谢产物将不能正常排除,患者机体将会出现不同程度的紊乱。UN绝大部分来源于蛋白质的分解代谢,其主要经肾脏排泄[15]。因此,当肾脏实质受到损害时,UN在血液中的浓度也将受到影响。
影响中国健康人BUN参考值的主要地理因素为海拔高度,随着海拔的升高,空气变得稀薄,相应的氧气量也减少。人体肾组织由于结构和功能的复杂性,其自身对氧的需求量非常大。海拔越高,缺氧程度越严重,肾损伤也越严重。出现该现象的原因是低氧血症使交感神经-肾上腺髓质的活性增强,促使血管紧张性增加,进而导致肾小动脉收缩,血管阻力增加,肾血流量和肾血浆浆流流量将减少,肾小球滤过率因而会降低,最终导致UN排出减少,BUN水平升高[16]。长期生活在高原地区的正常居民并未产生肾脏功能障碍的原因为:高原人生活在低氧环境下,机体适应性对低氧低压环境作出反应以改善肾组织低氧,使得缺氧导致的肾脏损害不会超过肾脏的代偿程度[17]。
中国健康人BUN参考值与年平均相对湿度和年降水量均呈负相关关系,从我国内陆到沿海,水分条件逐渐变得优越,年降水量、年平均相对湿度逐渐变大。因此,相对于沿海地区,内陆地区气候干燥,空气湿度较小,人体内水分蒸发较快,血液黏度相对较高,肾小球滤过率和肾血流量相对较低,进而导致内陆地区居民体内BUN水平相对较高。
相关分析结果显示:中国健康人BUN参考值与纬度呈正相关关系,与年平均气温呈负相关关系。我国由南向北纬度逐渐增大,年平均气温逐渐降低,所以纬度和年平均气温与中国健康人BUN参考值的相关性相反。因为纬度会带来气温条件的变化,因此纬度是通过气温条件来影响我国健康人BUN参考值的。我国南方地区以亚热带和热带季风气候为主,相对于北方地区,南方地区年平均气温高、年降水量大及年平均相对湿度大,南方地区居民体内的BUN水平较北方地区居民低。
自然地理环境是人类产生、繁衍、生活和发展的地方,是向人类提供各种资源和能源的场所。不同地区有不同的气候特征和不同的土壤环境等。由于地理条件存在差异,人的生理活动与病变特点也有区别,因此不同地区人体体质存在差异、生理特征存在明显的地域性,肾功能指标也不例外[18]。我国最早的医学典籍《黄帝内经》中的《素问·异法方宜论》论述了不同地域“一病而治各不同”的因地制宜的思想,如“东方之域,其治宜砭石”、“西方者,其治宜毒药”等[19]。本研究对不同预测模型进行对比选取了最优模型预测了中国2 322个市县地区健康人BUN预测参考值,初步探索了健康人BUN参考值与地理因素的关系,这与《黄帝内经》中“因地制宜”的思想是一致的。若已知某地区的纬度、海拔高度、年平均气温、年平均相对湿度和年降水量,将这些地理数据代入本研究选取的最优预测模型回归方程即可计算出该地区健康人BUN参考值的范围。例如北京,其上述各地理数据分别为39.89°、31.30 m、12 ℃、50%和571.9 mm, 将数据代入方程,可得到北京市健康人BUN参考值为(5.03±0.53) mmol·L-1。
在搜集了大量健康人BUN参考值的基础之上,本研究通过空间自相关分析,利用Moran指数确定了中国健康人BUN参考值与地理环镜之间并不是相互孤立的,其存在着很强的相关性;通过相关分析确定了与中国健康人BUN参考值相关的地理因素,通过共线性诊断确定了各地理因素之间存在多重共线性问题,主成分分析和岭回归构建模型避免了模型解释失效的问题,通过地统计分析选取了恰当的插值方法,最终拟合出了中国健康人BUN参考值地理分布图。本研究运用地理学的思路构建了地理因素和中国健康成年人BUN参考值的模型,并结合医学理论进行了相关机制的探讨,初步明确了中国健康人BUN参考值与地理环境之间的关系。
将地理因素对人体健康的影响纳入医学参考值制订的考量之中,有助于因地制宜地制订出适用于各地的医学参考值范围。未来关于各影响因子作用机制的研究还有待深入。
| [1] | 陶瑾. 维持性血液透析患者微炎症状态的临床研究[J]. 中国现代医学杂志, 2014, 24(4): 84–87. |
| [2] | 谭汉全, 尹雪梅. PTH、BUN及Cr联合检测在肾功能损伤早期诊断中的临床价值[J]. 海南医学院学报, 2015, 21(2): 197–199. |
| [3] | 井静, 葛淼, 赵安周, 等. 老年前期女性左心房内径参考值与地理环境的主成分分析[J]. 吉林大学学报:医学版, 2011, 37(6): 1144–1148. |
| [4] | 李艳芳. 血清胱抑素C与多种血清学指标在慢性心力衰竭患者中的表达及相关性[J]. 中外医学研究, 2014, 12(36): 8–10. |
| [5] | 危正南, 李涛, 张庆红, 等. MIF、TLR4、TNF-α水平在糖尿病肾病患者中的变化及其临床意义[J]. 疑难病杂志, 2016, 15(2): 165–168. |
| [6] | 徐建华. 计量地理学[M]. 北京: 高等教育出版社,2006: 120-130. |
| [7] | 张文彤, 邝春伟. SPSS统计分析基础教程[M]. 北京: 高等教育出版社,2011. |
| [8] | Marill KA. Advanced statistics:linear regression, part Ⅱ:multiple linear regression[J]. Acad Emerg Med, 2004, 11(1): 94–102. DOI:10.1197/acem.2004.11.issue-1 |
| [9] | Abdi H, Williams LJ. Principal component analysis[J]. Wiley Interdiscip Rev:Comput Stat, 2010, 2(4): 433–459. DOI:10.1002/wics.v2:4 |
| [10] | 刘新蕾, 葛淼, 王聪霞, 等. 地理环境波离散度参考值影响分析[J]. 东北师范大学学报:自然科学版, 2015, 47(1): 135–140. |
| [11] | Marquardt DW, Snee RD. Ridge regression in practice[J]. Am Stat, 1975, 29(1): 3–20. |
| [12] | Sheffield L, Whitford H, Cressie NA. Use of paired sample t-test in the real world[J]. Pract Otol, 2009, 102(3): 201–205. DOI:10.5631/jibirin.102.201 |
| [13] | 汤国安, 杨昕. ArcGIS地理信息系统空间分析实验教程[M]. 北京: 科学出版社,2006: 50-203. |
| [14] | Malauaduli AEO, Aziz MA, Kojima T, et al. Fixing collinearity instability using principal component and ridge regression analyses in the relationship between body measurements and body weight in Japanese black cattle[J]. J Anim Vet Adv, 2012, 3(12): 856–863. |
| [15] | 李著华, 邹平. 人体血液流变学[M]. 北京: 科学出版社,2016. |
| [16] | 王琰, 努尔曼古丽, 王引虎, 等. 进驻不同海拔高原健康男青年肾功能的变化[J]. 西南国防医药, 2011, 21(1): 24–26. |
| [17] | Gonzales GF. Hemoglobin and testosterone:importance on high altitude acclimatization and adaptation[J]. Rev Peru Med Exp Salud Publica, 2011, 28(1): 92–100. DOI:10.1590/S1726-46342011000100015 |
| [18] | 杨林生, 王五一, 谭见安, 等. 环境地理与人类健康研究成果与展望[J]. 地理研究, 2010, 29(9): 1571–1583. |
| [19] | 郑佐桓, 鞠宝兆. 《黄帝内经》治疗原则研究[J]. 辽宁中医药大学学报, 2014, 16(1): 88–91. |
 2017, Vol. 43
2017, Vol. 43


