扩展功能
文章信息
- 滕蓉, 杨陆一, 夏小雪, 王守东, 宁磊, 牡琦丽
- TENG Rong, YANG Luyi, XIA Xiaoxue, WANG Shoudong, NING Lei, MU Qili
- 基于遗传算法的不同类型错
 患者矢状向颅面结构的关联性分析
患者矢状向颅面结构的关联性分析 - Analysis on correlation of sagittal craniofacial structures with different classes of malocclusion based on genetic algorithms method
- 吉林大学学报(医学版), 2017, 43(04): 800-804
- Journal of Jilin University (Medicine Edition), 2017, 43(04): 800-804
- 10.13481/j.1671-587x.20170426
-
文章历史
- 收稿日期: 2016-12-02
 患者矢状向颅面结构的关联性分析
患者矢状向颅面结构的关联性分析
 患者矢状向颅面结构关系方程的参数,探讨其是否具有规律性。方法:
选取均角型错
患者矢状向颅面结构关系方程的参数,探讨其是否具有规律性。方法:
选取均角型错 患者240例,年龄8~18岁,分为安氏Ⅰ类组79例,安氏Ⅱ类组76例,安氏Ⅲ类组85例。每组随机选取10例为检验样本,其余为实验样本,实验样本用于获得GAS优化方程,检验样本用于误差分析。对所有患者的头颅侧位片进行头影测量分析,对各组测量参数[全颅底深度(Ba-N)、面中部深度(Ba-A)、颅底深度(Ba-S)、上颌后部深度(S-Ptm)、上颌骨基骨长度(Ptm-A)、下颌关节相对于颅底的距离(Ba-Ar)、下颌升支长度(Ar-Go)、下颌骨体长度(Go-PoG)、下面部深度(Ba-PoG)及颅底角(N-S-Ar)]进行独立样本t检验、单因素方差分析和逐步回归分析,识别颅面结构的相关影响因子;采用GAS优化方程参数获得相关方程,将优化方程预测值和实测值进行比较。结果:
安氏Ⅰ类、Ⅱ类和Ⅲ类组内比较,不同性别间各参数差异无统计学意义(P > 0.05),将同一类型不同性别组合并进行比较,Ba-A、Ptm-A、Ar-Go和Ba-PoG差异有统计学意义(P < 0.05)。相关分析,安氏Ⅰ类组,Ba-A与Ba-N呈正相关关系(r=0.683),Ptm-A与Go-PoG呈正相关关系(r=0.738),Ar-Go与Ba-PoG呈正相关关系(r=0.833)、与Go-PoG呈负相关关系(r=-0.560),Ba-PoG与Go-PoG呈正相关关系(r=0.669);安氏Ⅱ类组,Ba-A与Ba-PoG和Ba-N呈正相关关系(r=0.884,r=0.883),Ptm-A与Ba-A呈正相关关系(r=0.742),Ar-Go与Ba-PoG呈正相关关系(r=0.401)、与Go-PoG呈负相关关系(r=-0.317),Ba-PoG与Ba-A和Go-PoG呈正相关关系(r=0.883,r=0.488);安氏Ⅲ类组,Ba-A与Ba-N和Ba-PoG呈正相关关系(r=0.891,r=0.829),Ptm-A与Ba-A呈正相关关系(r=0.807)、与Ba-S呈负相关关系(r=-0.404),Ar-Go与S-Ptm呈正相关关系(r=0.548),Ba-PoG与Ba-A呈正相关关系(r=0.829)。使用GAS建立了不同错
患者240例,年龄8~18岁,分为安氏Ⅰ类组79例,安氏Ⅱ类组76例,安氏Ⅲ类组85例。每组随机选取10例为检验样本,其余为实验样本,实验样本用于获得GAS优化方程,检验样本用于误差分析。对所有患者的头颅侧位片进行头影测量分析,对各组测量参数[全颅底深度(Ba-N)、面中部深度(Ba-A)、颅底深度(Ba-S)、上颌后部深度(S-Ptm)、上颌骨基骨长度(Ptm-A)、下颌关节相对于颅底的距离(Ba-Ar)、下颌升支长度(Ar-Go)、下颌骨体长度(Go-PoG)、下面部深度(Ba-PoG)及颅底角(N-S-Ar)]进行独立样本t检验、单因素方差分析和逐步回归分析,识别颅面结构的相关影响因子;采用GAS优化方程参数获得相关方程,将优化方程预测值和实测值进行比较。结果:
安氏Ⅰ类、Ⅱ类和Ⅲ类组内比较,不同性别间各参数差异无统计学意义(P > 0.05),将同一类型不同性别组合并进行比较,Ba-A、Ptm-A、Ar-Go和Ba-PoG差异有统计学意义(P < 0.05)。相关分析,安氏Ⅰ类组,Ba-A与Ba-N呈正相关关系(r=0.683),Ptm-A与Go-PoG呈正相关关系(r=0.738),Ar-Go与Ba-PoG呈正相关关系(r=0.833)、与Go-PoG呈负相关关系(r=-0.560),Ba-PoG与Go-PoG呈正相关关系(r=0.669);安氏Ⅱ类组,Ba-A与Ba-PoG和Ba-N呈正相关关系(r=0.884,r=0.883),Ptm-A与Ba-A呈正相关关系(r=0.742),Ar-Go与Ba-PoG呈正相关关系(r=0.401)、与Go-PoG呈负相关关系(r=-0.317),Ba-PoG与Ba-A和Go-PoG呈正相关关系(r=0.883,r=0.488);安氏Ⅲ类组,Ba-A与Ba-N和Ba-PoG呈正相关关系(r=0.891,r=0.829),Ptm-A与Ba-A呈正相关关系(r=0.807)、与Ba-S呈负相关关系(r=-0.404),Ar-Go与S-Ptm呈正相关关系(r=0.548),Ba-PoG与Ba-A呈正相关关系(r=0.829)。使用GAS建立了不同错 类型矢状向颅面结构的关系方程。安氏Ⅰ类,Ba-A(mm)=10.9639+0.8598×Ba-N,Ptm-A(mm)=6.8976+0.5570×Go-PoG,Ar-Go(mm)=-2.5482+0.5118×Ba-PoG-0.5272×Go-PoG,Ba-PoG(mm)=17.515 6+1.021 3×GO-POG;安氏Ⅱ类,Ba-A(mm)=-2.121 3+0.567 6×Ba-PoG+0.513 2×Ba-N,Ptm-A(mm)=13.788 7+0.349 4×Ba-A,Ar-Go(mm)=2.447 7+0.368 8×Ba-POG-0.427 9×Go-PoG,Ba-PoG(mm)=-7.140 2+0.751 3×Ba-A+0.295 4×Go-PoG;安氏Ⅲ类,Ba-A(mm)=3.281 0+0.545 3×Ba-N+0.394 4×Ba-PoG,Ptm-A(mm)=3.535 8+0.631×Ba-A-0.614 2×Ba-S,Ar-Go(mm)=-9.002 1+1.004 3×S-Ptm,Ba-PoG(mm)=-2.091 2+1.057 5×Ba-A。GAS建立的方程预测值与实测数据比较差异无统计学意义(P > 0.05)。结论:
采用GAS建立了矢状向错
类型矢状向颅面结构的关系方程。安氏Ⅰ类,Ba-A(mm)=10.9639+0.8598×Ba-N,Ptm-A(mm)=6.8976+0.5570×Go-PoG,Ar-Go(mm)=-2.5482+0.5118×Ba-PoG-0.5272×Go-PoG,Ba-PoG(mm)=17.515 6+1.021 3×GO-POG;安氏Ⅱ类,Ba-A(mm)=-2.121 3+0.567 6×Ba-PoG+0.513 2×Ba-N,Ptm-A(mm)=13.788 7+0.349 4×Ba-A,Ar-Go(mm)=2.447 7+0.368 8×Ba-POG-0.427 9×Go-PoG,Ba-PoG(mm)=-7.140 2+0.751 3×Ba-A+0.295 4×Go-PoG;安氏Ⅲ类,Ba-A(mm)=3.281 0+0.545 3×Ba-N+0.394 4×Ba-PoG,Ptm-A(mm)=3.535 8+0.631×Ba-A-0.614 2×Ba-S,Ar-Go(mm)=-9.002 1+1.004 3×S-Ptm,Ba-PoG(mm)=-2.091 2+1.057 5×Ba-A。GAS建立的方程预测值与实测数据比较差异无统计学意义(P > 0.05)。结论:
采用GAS建立了矢状向错 颅面结构的优化关系方程,且其定量具有规律性。
颅面结构的优化关系方程,且其定量具有规律性。 类型 矢状向颅面结构 相关关系分析 遗传算法
类型 矢状向颅面结构 相关关系分析 遗传算法 在颅面发育过程中,由于遗传、演化和环境因素的影响,可导致颅面及错牙合畸形的产生,影响正常的生长发育[1]。制订矫治计划时,明确错牙合发生的机制尤为重要,以往研究重点多放在上下颌关系上,对颅面内部结构之间的相关性报道较少,而如何定量识别颅面部各测量参数之间的相关关系,是该项研究的关键技术。遗传算法(genetic algorithms,GAS)由Holland[2]首先提出,是一类借鉴生物界自然选择和自然遗传机制的全局搜索算法,其典型的应用领域之一就是参数优化问题[3-5]。目前,GAS在医学领域也有一定的应用[6-7],但使用GAS建立矢状向错牙合颅面结构的优化关系方程国内外尚未见报道。本研究采用GAS建立不同错牙合类型矢状向颅面结构间的相关方程,直观地定量表达颅面内部结构间的相互关系,为临床工作及科研提供参考。
1 资料与方法 1.1 研究对象选择2012—2016年在吉林大学口腔医院正畸科就诊的初诊错牙合患者,按以下标准进行筛选:年龄8~18岁;为防止上下颌骨垂直向关系不谐调对颅面形态产生混杂因素的影响,同时要求22° < 下颌平面角(FH-MP) < 32°,29° < 下颌平面角(SN-MP) < 40°,62% < 后面高与前面高比值(S-Go/N-Me) < 68%;汉族,身体健康,上下颌骨发育正常,无影响口颌系统发育的疾病,无外伤史;未接受过正畸治疗,牙列完整(第三磨牙无要求),牙齿形态、数目无异常,无颞下颌关节疾病;X线片清晰。
1.2 分组筛选出符合标准的病例240例,根据Angle分类法将符合纳入标准的患者分为3组:安氏Ⅰ类组79例,男性44例,女性35例,平均年龄(13.73±3.03) 岁,双侧尖牙和磨牙为Ⅰ类关系,0°<上下齿槽座角(ANB)<5°;安氏Ⅱ类组76例,男性44例,女性32例,平均年龄(13.65±3.62) 岁,双侧尖牙和磨牙为Ⅱ类关系,ANB≥5°;安氏Ⅲ类组85例,男性42例,女性43例,平均年龄(13.64±4.33) 岁,双侧尖牙和磨牙为Ⅲ类关系,ANB≤0°。从3组中分别随机抽取10例患者为检验样本,其余为实验样本。检验样本用于误差分析,实验样本用于获得GAS优化方程。
1.3 方法所有患者均经同一名医师严格按照要求、由同一台设备拍摄头颅侧位片,存储于Winceph8.0头影测量软件的图像管理系统中(日本Rise公司)并进行测量分析(主要分析方法为Coben分析法)。由研究者在计算机上进行定点测量,每次测量间隔1周,共测3次,取平均值,记为最终结果。
1.4 GAS参数优化和方程建立GAS主要参数:种群规模80 000,选择率0.05,交叉率0.1,变异率0.2,进化代数30。需要优化的方程结构为:y=xx(1)+xx(2)×p(1, i),y=xx(1)+xx(2)×p(1, i) +xx(3)×p(2, i)。式中,xx(i)为需要优化的参数,p(1,i)和p(2,i)为影响因子。采用GAS按照上述方程结构根据影响因子个数建立不同错牙合类型矢状向颅面内部结构间的相关方程。
1.5 统计学分析采用SPSS22.0统计软件进行统计学分析。各测量参数[全颅底深度(Ba-N)、面中部深度(Ba-A)、颅底深度(Ba-S)、上颌后部深度(S-Ptm)、上颌骨基骨长度(Ptm-A)、下颌关节相对于颅底的距离(Ba-Ar)、下颌升支长度(Ar-Go)、下颌骨体长度(Go-PoG)、下面部深度(Ba-PoG)及颅底角(N-S-Ar)]均以x±s表示。同一类型不同性别组间各参数比较采用独立样本t检验,3组间不同参数比较采用单因素方差分析,组间两两比较采用SNK-q检验。采用逐步回归分析法,确定各参数的关键影响因子。采用独立样本t检验对检验样本进行GAS预测值与实测值比较即误差分析。以α=0.05为检验水准。
2 结果 2.1 安氏Ⅰ类、Ⅱ类和Ⅲ类组患者各测量参数对同一类型不同性别组患者Ba-N、Ba-A、Ba-S、S-Ptm、Ptm-A、Ba-Ar、Ar-Go、Go-PoG、Ba-PoG和N-S-Ar分别进行独立样本t检验,结果显示:不同性别患者间各参数比较差异均无统计学意义(P>0.05)。故将同一类型不同性别参数合并,并进行组间比较,Ba-A、Ptm-A、Ar-Go和Ba-PoG差异有统计学意义(P<0.05)。见表 1。
| (x±s) | |||||||||||
| Group | n | Ba-N(l/mm) | Ba-A(l/mm) | Ba-S(l/mm) | S-Ptm(l/mm) | Ptm-A(l/mm) | Ba-Ar(l/mm) | Ar-Go(l/mm) | Go-PoG(l/mm) | Ba-PoG(l/mm) | N-S-Ar(θ/°) |
| Angle ClassⅠ | 79 | 89.51±7.07 | 87.92±10.23△ | 28.39±5.37 | 17.41±2.96 | 42.55±5.17*△△ | 13.46±4.29 | 6.13±4.88△ | 64.00±7.62 | 82.88±9.92△ | 122.87±5.90 |
| Angle ClassⅡ | 76 | 90.19±7.02△△ | 91.14±7.11△△ | 28.97±4.68 | 17.54±2.52 | 45.63±3.35△△ | 12.43±4.41 | 4.88±3.29△△ | 63.25±5.23 | 79.96±6.59△△ | 123.14±4.87 |
| Angle ClassⅢ | 85 | 86.32±7.88 | 84.31±6.84 | 27.16±5.79 | 17.03±2.60 | 40.06±3.46 | 13.51±4.41 | 8.14±4.38 | 65.41±6.97 | 87.07±8.72 | 121.55±5.30 |
| P | 0.096 | 0.003 | 0.510 | 0.703 | 0.000 | 0.344 | 0.005 | 0.369 | 0.002 | 0.383 | |
| P < 0.01 vs Angle ClassⅡ group; △P < 0.05, △△P < 0.01 vs Angle Class Ⅲ group | |||||||||||
3组间比较,Ba-A、Ptm-A、Ar-Go和Ba-PoG差异均有统计学意义(P<0.05),其余指标差异无统计学意义(P>0.05)。Ba-A和Ptm-A:安氏Ⅱ类>安氏Ⅰ类>安氏Ⅲ类;Ar-Go和Ba-PoG:安氏Ⅲ类>安氏Ⅰ类>安氏Ⅱ类。3组间两两比较,与安氏Ⅱ类组比较,安氏Ⅰ类组患者Ba-N、Ba-PoG、Ba-Ar、S-Ptm、Go-PoG和Ba-PoG差异均无统计学意义(P>0.05),Ptm-A差异有统计学意义(P<0.01)。与安氏Ⅲ类组比较,安氏Ⅰ类组Ba-N、Ba-S、S-Ptm和Go-PoG差异无统计学意义(P>0.05),Ptm-A、Ar-Go和Ba-PoG差异有统计学意义(P<0.05或P<0.01);安氏Ⅱ类组患者Ba-N、Ba-A、Ptm-A、Ar-Go和Ba-PoG差异有统计学意义(P<0.01),Ba-S、S-Ptm、Go-PoG和Ba-Ar差异无统计学意义(P>0.05)。见表 1。
2.2 逐步回归分析法识别关键影响因子采用SPSS 22.0统计软件通过逐步回归分析法识别颅面结构关键因子。安氏Ⅰ类组:Ba-A与Ba-N呈正相关关系(r=0.683),Ptm-A与Go-PoG呈正相关关系(r=0.738),Ar-Go与Ba-PoG呈正相关关系(r=0.833)、与Go-PoG呈负相关关系(r=-0.560),Ba-PoG与Go-PoG呈正相关关系(r=0.669);安氏Ⅱ类组:Ba-A与Ba-PoG和Ba-N呈正相关关系(r=0.884,r=0.883),Ptm-A与Ba-A呈正相关关系(r=0.742),Ar-Go与Ba-PoG呈正相关关系(r=0.401)、与Go-PoG呈负相关关系(r=-0.317),Ba-PoG与Ba-A和Go-PoG呈正相关关系(r=0.883,r=0.488);安氏Ⅲ类组:Ba-A与Ba-N和Ba-PoG呈正相关关系(r=0.891,r=0.829),Ptm-A与Ba-A呈正相关关系(r=0.807)、与Ba-S呈负相关关系(r=-0.404),Ar-Go与S-Ptm呈正相关关系(r=0.548),Ba-PoG与Ba-A呈正相关关系(r=0.829)。
2.3 GAS参数优化相关方程采用GAS建立了不同错牙合类型Ba-A、Ptm-A、Ar-Go和Ba-PoG的优化关系方程。安氏Ⅰ类组:Ba-A(mm)=10.9639+0.8598×Ba-N,Ptm-A(mm)=6.8976+0.5570×Go-PoG,Ar-Go(mm)=-2.5482+0.5118×Ba-PoG-0.5272×Go-PoG,Ba-PoG(mm)=17.5156+1.0213× Go-PoG;安氏Ⅱ类组:Ba-A(mm)=-2.121 3+ 0.567 6×Ba-PoG+0.513 2×Ba-N, Ptm-A(mm)= 13.788 7+0.349 4×Ba-A, Ar-Go(mm)=2.447 7+0.368 8×Ba-PoG-0.4279×Go-PoG, Ba-PoG(mm)=-7.140 2+0.751 3×Ba-A+0.295 4×Go-PoG;安氏Ⅲ类组:Ba-A(mm)=3.281 0+0.545 3× Ba-N+0.394 4×Ba-PoG,Ptm-A(mm)=3.535 8+0.631 0×Ba-A-0.614 2×Ba-S,Ar-Go(mm) =-9.002 1+1.004 3×S-Ptm,Ba-PoG(mm)=-2.091 2+1.057 5×Ba-A。
2.4 误差分析GAS建立的方程预测值与实测数据比较差异均无统计学意义(P>0.05)。见表 2。
| (n=10, x±s) | |||||||||||||||
| Group | Angle ClassⅠ | Angle ClassⅡ | Angle ClassⅡ | Angle ClassⅢ | |||||||||||
| Ba-A | Ptm-A | Ar-Go | Ba-PoG | Ba-A | Ptm-A | Ar-Go | Ba-PoG | Ba-A | Ptm-A | Ar-Go | Ba-PoG | ||||
| Measured value | 87.68±5.28 | 44.82±5.33 | 4.78±3.71 | 84.59±7.36 | 87.07±5.38 | 16.38±1.61 | 3.95±1.41 | 75.80±4.57 | 86.77±4.29 | 41.57±4.81 | 8.20±4.56 | 92.62±8.21 | |||
| GAS | 87.52±5.55 | 45.12±4.77 | 4.49±2.60 | 87.61±8.76 | 87.18±4.36 | 17.31±1.66 | 4.32±1.35 | 76.63±4.40 | 85.84±3.17 | 40.81±3.99 | 7.87±3.88 | 89.67±6.66 | |||
| P | 0.870 | 0.614 | 0.171 | 0.432 | 0.535 | 0.249 | 0.264 | 0.884 | 0.447 | 0.888 | 0.244 | 0.600 | |||
在正畸、正颌的临床诊断和制订治疗计划时,正确评价上下颌骨的矢状位置关系具有重要的意义[8]。在以往的研究中,大多数学者将ANB角、AB平面角、Wits值和上下颌骨矢状不调指标(anterposterior dysplasia indicator, APDI)等作为评价上下颌矢状关系的标志[9-12]。本实验利用Coben分析法对不同类型错牙合畸形患者的头颅侧位片进行头影测量分析,更深入地了解颅面内部的相关性及补偿机制。
本研究结果显示:3组间Ba-N比较,安氏Ⅱ类>安氏Ⅰ类>安氏Ⅲ类,与陈红等[13-14]采用几何形态测量法得出的研究结果相同;3组间Ba-A和Ptm-A比较,安氏Ⅱ类>安氏Ⅰ类>安氏Ⅲ类,差异均有统计学意义,与不同错牙合类型上颌突度不同相一致;而3组间Ba-S和S-Ptm比较差异无统计学意义,说明后颅底和上颌后部对上颌骨矢状向的位置影响不大,造成错牙合的原因为上颌骨基骨长度不同,可能为机体代偿所导致的协调性变化;3组间Ar-Go和Ba-PoG比较,安氏Ⅲ类>安氏Ⅰ类>安氏Ⅱ类,差异均有统计学意义,与不同错牙合类型下颌突度不同相一致;而3组间Ba-Ar和Go-PoG比较差异虽无统计学意义,但从数据中看出安氏Ⅱ类下颌骨位置相对靠后,安氏Ⅲ类下颌骨位置相对靠前。本研究结果显示:不同错牙合类型患者颅底角并无明显差异,不能说明后颅底的形态差异能够影响上下颌骨的位置,表明3组患者后颅底结构相对稳定。这与Melsen[15]的研究结果相同,表明不同错牙合类型颅底角处于动态平衡中;Bhatia等[16]的纵向研究也证实了这种稳定性。
一般认为,7岁后后颅底的前部分及中央部分很少生长,其结构的变化主要是通过颅腔扩大和鼻骨区域的骨改建。Dhopatkar等[17]认为:后颅底对下颌的大小和位置有影响,而另有学者[18]则持相反观点。本研究结果显示:后颅底并不能影响下颌骨的位置,但后颅底长度和下颌骨长度互呈正相关关系。不同种错牙合类型,影响颅面内部各指标的因素均不同,本实验建立的方程可直观反映颅面内部矢状向各指标间的相互关系。以Ptm-A为例,安氏Ⅰ类中,与其呈正相关关系的指标为Go-PoG;安氏Ⅱ类中,与其呈正相关关系的指标为Ba-A;安氏Ⅲ类中,与其呈正相关关系的指标为Ba-A,与其呈负相关关系的指标为Ba-S。本实验采用逐步回归分析法识别关键影响因子,采用GAS对其进行参数优化,方程预测值与实测值比较差异无统计学意义,表明错牙合患者矢状向颅面结构的定量具有规律性,精度高,对临床及科研工作有指导意义。
颅面部是内部高度相关的复合体,只有熟悉不同错牙合类型发生的机制,了解颅面部各部分的关联性,才能更好地诊断和制订矫治计划。本研究以Coben分析法为基本方法、采用GAS建立相关方程,可更精确地了解颅面内部结构的相互关系,但尚缺乏对牙性问题的研究,还需进一步探讨。
| [1] | 陈扬熙. 口腔正畸学-基础、技术与临床[M]. 北京: 人民卫生出版社,2012. |
| [2] | Holland JH. Adaptation in natural and artificial systems:an introductory analysis with applications to biology, control, and artificial intelligence[M]. 2nd ed. Cambridge: MIT Press, 1992. |
| [3] | 秦华, 康朝红, 刘鑫淼, 等. 基于BTO多目标遗传算法的播种机性能优化设计[J]. 农机化研究, 2017, 39(6): 145–149. |
| [4] | 陈顺立. 农业机器人路径优化及轨迹跟踪研究-基于遗传算法[J]. 农机化研究, 2017, 39(8): 17–21. |
| [5] | 李鸿雁, 赵娟, 王玉新. 扩域搜索遗传算法优化马斯京根参数及其应用[J]. 吉林大学学报:地球科学版, 2011, 41(3): 861–865. |
| [6] |
董妍, 杨陆一, 朱惠芳, 等.
遗传算法预测不同错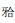 类型牙冠宽度[J]. 口腔医学研究, 2015, 31(7): 728–731. 类型牙冠宽度[J]. 口腔医学研究, 2015, 31(7): 728–731.
|
| [7] | 许良凤, 林辉, 罗珣, 等. 基于并行遗传算法的Otsu双阈值医学图像分割[J]. 工程图学学报, 2011, 32(2): 88–92. |
| [8] |
蔡颖, 唐小荣, 王翔.
骨性Ⅱ类错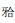 颌骨矢状关系评价指标的相关分析[J]. 南通大学学报:医学版, 2013, 33(5): 449–450. 颌骨矢状关系评价指标的相关分析[J]. 南通大学学报:医学版, 2013, 33(5): 449–450.
|
| [9] |
刘东旭, 张磊, 王春玲, 等.
安氏Ⅱ类1分类错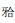 上下颌基骨前后关系诊断指标的可靠性评价[J]. 华西口腔医学杂志, 2006, 24(4): 323–327. 上下颌基骨前后关系诊断指标的可靠性评价[J]. 华西口腔医学杂志, 2006, 24(4): 323–327.
|
| [10] | Freeman RS. Adjusting ANB angles to reflect the effect of maxillary position[J]. Angle Orthod, 1981, 51(2): 161–171. |
| [11] | Sarhan OA. A new cephalometric parameter to aid in dental base relationship[J]. Angle Orthod, 1990, 60(1): 59–63. |
| [12] | Yang SD, Suhr CH. F-H to AB plane angle(FABA) for assessment of anteroposterior jaw relationship[J]. Angle Orthod, 1995, 65(3): 223–232. |
| [13] |
陈红, 丁寅, 郭涛, 等.
骨性Ⅱ类错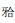 的颅底形态研究[J]. 口腔医学, 2006, 26(4): 298–300. 的颅底形态研究[J]. 口腔医学, 2006, 26(4): 298–300.
|
| [14] |
陈红, 丁寅.
骨性Ⅲ类错 的颅底形态研究[J]. 临床口腔医学杂志, 2006, 22(5): 281–283. 的颅底形态研究[J]. 临床口腔医学杂志, 2006, 22(5): 281–283.
|
| [15] | Melsen B. The cranial base:The postnatal development of the cranial base studied histologically on human autopsy material[J]. Acta Odontol Scand, 1974, 66(6): 689–691. |
| [16] | Bhatia SN, Leighton BC. A manual of facial growth[M]. Oxford: Oxford University Press, 1993. |
| [17] | Dhopatkar A, Bhatia S, Rock P. An investigation into the relationship between the cranial base angle and malocclusion[J]. Angle Orthod, 2002, 72(5): 456–463. |
| [18] | Rothstein T, Yoon-Tarlie C. Dental and facial skeletal characteristics and growth of males and females with class Ⅱ, division 1 malocclusion between the ages of 10 and 14(revisited)-part Ⅰ:characteristics of size, form, and position[J]. Am J Orthod Dentofacial Orthop, 2000, 117(3): 320–332. DOI:10.1016/S0889-5406(00)70237-X |
 2017, Vol. 43
2017, Vol. 43


