扩展功能
文章信息
- 陈庆生, 陈笑风, 单晔杰, 丁熙, 王慧明
- CHEN Qingsheng, CHEN Xiaofeng, SHAN Yejie, DING Xi, WANG Huiming
- 松质骨和皮质骨厚度对种植体周围应力分布的影响
- Influence of thickness of cancellous bone and cortical bone in stress distribution in vicinity of an implant
- 吉林大学学报(医学版), 2016, 42(02): 204-209
- Journal of Jilin University (Medicine Edition), 2016, 42(02): 204-209
- 10.13481/j.1671-587x.20160203
-
文章历史
- 收稿日期: 2015-07-27
2. 浙江大学应用力学研究所, 浙江杭州 310027;
3. 温州医科大学附属第一医院口腔科, 浙江温州 325035
2. Institute of Applied Mechanics, Zhejiang University, Hangzhou 310027, China;
3. Department of Stomatology, First Hospital, Wenzhou Medical University, Wenzhou 325035, China
近年来,种植义齿修复已广泛应用于牙列缺损及缺失患者。但是,临床上容易出现由于各种因素导致的种植失败,原因主要是种植体周围炎和种植体颈部发生的骨吸收。种植体颈部的皮质骨处容易出现应力集中,这种应力集中使得局部骨质的压应力过大而导致骨吸收[1],从而导致种植体的松动,进而影响种植体和义齿的使用效果。因此,临床进行种植修复时应尽可能地优化可控因素,以避免种植体颈部区域周围出现过大的应力集中。
影响种植区应力分布的因素主要包括材料因素、几何因素和载荷因素三类。材料因素主要包括骨组织和种植体的密度、弹性模量、泊松比等材料参数;几何因素主要包括松质骨和皮质骨的厚度、受种植区域的拓扑结构、种植体的形状等;载荷因素主要包括受力面、载荷的大小和方向等。其中载荷因素会受到材料因素和几何因素的影响。从临床修复的可控性来说,材料因素几乎是不可控的,几何因素是可控的,而载荷因素部分可通过几何因素来调控。已有研究[2, 3]表明:种植区的几何因素对种植体的植入效果有重要影响。对于不同的患者,有2个体现显著个体差异性的几何参数,即种植体周围松质骨和皮质骨的总厚度以及松质骨和皮质骨的厚度之比。这2个几何参数包含了种植体周围松质骨和皮质骨几何尺寸差异的所有情况,并且其在临床修复手术中均可以通过骨量增减来调节[4]。
既然几何因素是最明显的可控因素,那么有必要建立模型来研究几何因素是怎样对种植体及骨组织内的应力分布产生影响。采用有限元法研究种植体周围骨组织应力分布的研究已经取得了一些有意义的成果。Hansson[5]利用轴对称的有限元模型研究了种植体周围在水平向和垂直向载荷时的应力分布,指出了2个方向的载荷所导致的最大应力分布在空间的不同位置。Chun等[2]利用二维有限元方法探讨了不同的种植体形状对种植体周围应力分布的影响,提出了一种较优的种植体的形状,以尽量降低种植体周围的最大应力值。Kitamura等[6]建立了9种代表不同程度骨吸收的骨组织模型并使用三维有限元法来进行分析,指出一定程度的骨吸收可能是骨组织与应力在生物力学的相容性上的一种表现形式。有研究者[7, 8]对各种几何因素对种植体周围应力分布的影响进行了探讨,对种植体、骨组织、义齿、载荷条件等做了合理的简化,利用有限元法分析得出了许多重要结果,为临床实践和种植体设计提供了极具价值的指导。近年来,随着一系列技术的发展,结合CT扫描和有限元分析来研究种植体问题成了热点,研究者们[9, 10, 11, 12]使用这种技术也取得了许多成果。
虽然对各种情况下种植体周围应力分布的研究较多,但是迄今为止尚未见综合考虑种植体周围松质骨和皮质骨的比例及总厚度来研究应力分布变化情况的报道。本研究采用种植体周围松质骨和皮质骨的总厚度以及松质骨和皮质骨厚度之比来研究种植体周围的应力分布。本研究建立简化的种植体、骨组织和义齿模型,取松质骨和皮质骨的比值分别为3:1、2:1、1:1、1:2和1:3,两者的总厚度分别取0.5、1.0、2.0、3.0和4.0 mm,进行有限元分析。
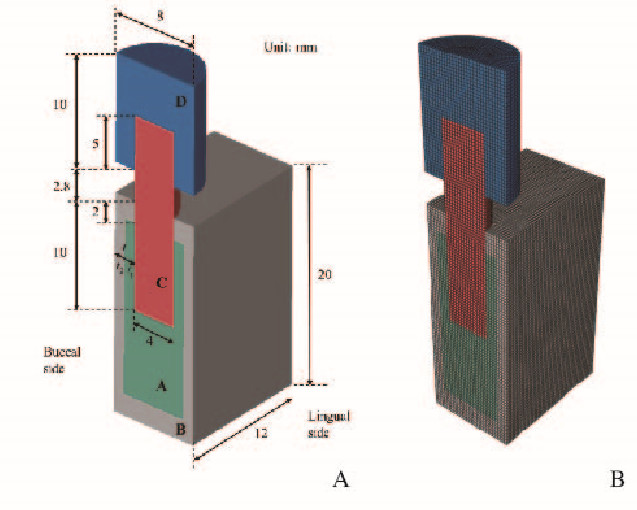
1 材料与方法 1.1 有限元模型使用有限元软件Abaqus建立简化的颌骨三维有限元模型,颌骨模型的建立均采用颊舌对称的形态。骨组织设计为外层是皮质骨,中间是松质骨的结构[6]。种植体设计为直径为4.0 mm的圆柱形植入体,其中植入下颌骨的长度为10.0 mm,具体形状和尺寸见图 1A(插页一)。本模型具有对称性,因此为了提高计算效率只需建立一半的模型,并合理地设定对称性边界条件,然后进行分析。
|
| A:a,Cancellous bone;b,Cortical bone;c,Implant;d: Crown. 图1 松质骨、皮质骨、种植体和牙冠的简化模型示意图(A)和模型的网络划分(B) Fig.1 Schematics of simplified model comprising cortical bone, cancellous bone,implant, and artificial teeth (A) and meshing of model(B) |
本研究中的皮质骨、松质骨、种植体和义齿均假设为各向同性、均质连续的线弹性材料,其材料力学参数见表 1。
| (x±s) | ||
| Material | Young’s modulus (P/GPa) | Poisson’s ratio |
| Titanium implant | 116.0 | 0.35 |
| Ceramic crown | 70.0 | 0.19 |
| Cortical bone | 13.4 | 0.30 |
| Cancellous bone | 1.5 | 0.30 |
皮质骨底面受到位移和转角的约束,避免刚体位移。骨界面与种植体是完全性骨性结合,各界面受力时未出现互相滑动,其连接方式为完全固定的绑定约束。陶瓷质牙冠和皮质骨、种植体的接触面均无相对滑动,其连接关系均为绑定约束。
1.4 加载条件陶瓷质牙冠受到的力可分解为水平和垂直2个分量。为了尽量模拟真实咀嚼时产生的作用力,本实验模拟假设陶瓷质牙齿的上表面同时受到2个力的作用,1个是向下的轴向压力, 1个是颊侧向舌侧的力的作用,如图 1A(插页一)所示,图 1A并未标注加载力的方向,力的大小均为100 N [10]。
1.5 网格划分本模型全部采用结构化六面体单元划分网格,如图 1B(插页一)所示。网格质量优秀,数量众多,能够保证计算的精确性。
1.6 研究分组如图 1A(插页一)所示:种植体外表面与骨皮质外侧的距离为t。令t=t1+t2,其中t1为松质骨的厚度,t2为皮质骨的厚度。对应于不同患者的生理情况,不仅t会有差异,松质骨和皮质骨的厚度比即t1和t2的厚度比也存在差异。本研究对t1:t2取5组不同的比值,即3:1、2:1、1:1、1:2和1:3,分别建立三维有限元模型观察总厚度(t)的大小对模型的最大应力值和应力分布的影响。t分别取为0.5、1.0、2.0、3.0和4.0 mm。
1.7 分析计算编写Python脚本程序,在服务器上应用Abaqus有限元软件分析不同松质骨和皮质骨总厚度及其比例下种植体骨颈部骨组织的von Mises应力分布。
2 结 果 2.1 皮质骨的应力分布皮质骨颈部的最大von Mises应力值随总厚度(t)的变化如图 2所示。图 2中的5条线分别对应t1:t2取5组不同的比值(3:1、2:1、1:1、1:2、1:3)。由图 2可见:各条曲线均在2.0 mm处取得极小值——当t小于2.0 mm时,S1随着t的减少而显著增加;而当t大于2.0 mm时,S1随着t的增加而平缓地增加。

|
| 图2 不同总厚度时皮质骨颈部的最大von Mises应力值 Fig.2 Maximum von Mises stress values at neck of cortical bone with different total thickness |
t1:t2=1:1 条件下皮质骨内应力分布随着t的变化规律如图 3和4(插页一)所示。随着骨皮质厚度的增加,应力分布总体上趋于均匀化,应力集中可能造成的皮质骨骨吸收的危险性也随之降低。当t较小时,皮质骨的底部也出现了红色区域的应力集中。上述结果提示当松质骨和皮质骨的总厚度较小时,皮质骨底部是否容易骨吸收也是值得研究的问题。

|
| 图3 不同总厚度时整个皮质骨的最大von Mises应力值 Fig.3 Maximum von Mises stress values of whole cortical bone with different total thickness |

|
| t:t2=1;A-E:t=0.5,1.0,2.0,3.0,and 4.0 mm. 图4 皮质骨上的应力分布 Fig.4 Stress distribution on cortical bone |
种植体内的最大von Mises应力值随总厚度t的变化如图 5所示。图 5中的5条线分别对应取5组不同的比值(3:1、2:1、1:1、1:2、1:3)。种植体上的各个最大应力随着松质骨和皮质骨的总厚度(t)的增大而单调递减,在0~2.0 mm减小速度较快,在2.0~4.0 mm减小速度较慢。因此,总厚度(t)的增大有利于减小种植体上的应力集中。图 6(插页一)是在t1:t2=1:1条件下种植体表面的应力分布图,可见随着总厚度的增大,种植体上的最大应力值减小,应力分布变得均匀。

|
| 图5 不同总厚度时种植体的最大von Mises应力值 Fig.5 Maximum von Mises stress values of implant with different total thickness |

|
| t:t2=1;A-E:t=0.5,1.0,2.0,3.0,and 4.0 mm. 图6 种植体上的应力分布 Fig.6 Stress distribution on implant |
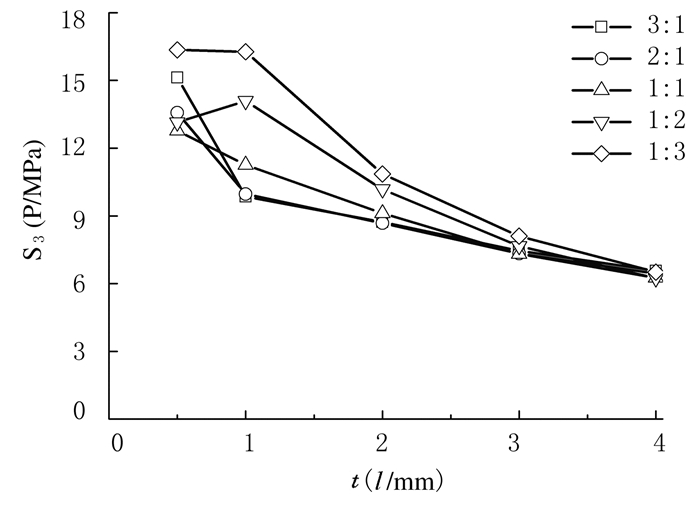
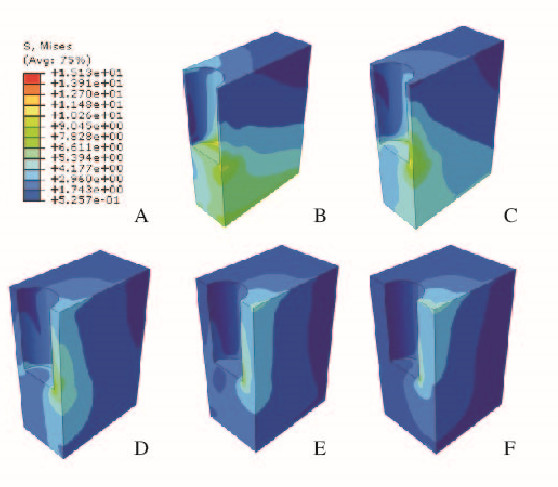
松质骨内的最大von Mises应力值S3 随厚度(t)的变化如图 7所示。图 7中的5条线分别对应t1:t2取5组不同的比值(3:1、2:1、1:1、1:2、1:3)。由图 7可见:松质骨内的最大应力随着松质骨和皮质骨的总厚度(t)的增大而单调递减,在0.5~2.0 mm区间减小较快,在2.0~4.0 mm区间减小较慢。因此一般而言,总厚度(t)的增大有利于减小松质骨上的应力集中。图 8(插页一)是在t1:t1=1:1 条件下松质骨表面的应力分布图,随着总厚度(t)的增大,松质骨上的最大应力值减小,应力分布变得均匀。
|
| 图7 不同总厚度时松质骨的最大von Mises应力值 Fig.7 Maximum von Mises stress of cancellous bone with different total thickness |
|
| t:t2=1;A-E:t=0.5,1.0,2.0,3.0,and 4.0 mm. 图8 松质骨上的应力分布 Fig.8 Stress distribution on cancellous bone |
本文作者采用三维有限元方法观察在侧向力和轴向力的加载条件下不同厚度和比例的松质骨和皮质骨对种植体周围的应力分布的影响。
本研究中图 3、4和8分析结果显示:皮质骨内的最大应力值较松质骨高一个量级。发生这种状况是由于皮质骨的弹性模量较松质骨高,在外力作用下会发生“应力屏蔽”效应,使得应力主要集中在种植体颈部的皮质骨区域[13]。另外,本文作者对图 3、4、6和8的分析发现:t1:t2值对皮质骨颈部、种植体、松质骨的最大应力值有重要影响。导致种植体失效的诸多因素中,种植体周围的皮质骨的骨吸收是主要因素,而皮质骨和种植体内的应力集中则是导致骨吸收的主要原因[12]。那么,是否存在一个最佳的松质骨和皮质骨之比,能够最大程度地降低在两者的总厚度(t)相同的条件下皮质骨和种植体内的最大应力值?如图 3和4所示,当t为0.5或1.0 mm时,皮质骨内的最大应力值随着松质骨厚度与皮质骨厚度比值的减小而减小(即皮质骨厚度所占总厚度的比例增大),直到t1:t2 时减小不再明显。当t≥2.0 mm时,皮质骨内的最大应力值与松质骨厚度与皮质骨厚度比值的关系不明显。如图 6所示:种植体中的最大应力值随着 t1与t2比值的减小而显著减小(即皮质骨厚度所占总厚度的比例增大),当t1:t2≤1:2时减小速率明显降低,表明提高皮质骨的厚度所占总厚度比例能有效降低皮质骨和种植体内的应力集中,所以种植手术中应尽量保证皮质骨的厚度达到松质骨厚度的2倍以上,以避免应力集中导致骨吸收,造成种植失败。
模拟结果表明:①皮质骨、种植体和松质骨内的最大应力值随着皮质骨和松质骨总厚度的增大而减小;②对于不同厚度比例的松质骨和皮质骨,种植体颈部皮质骨内的最大应力在松质骨和皮质骨的总厚度为2.0 mm时取得最小值,当总厚度小于2.0 mm时,种植体颈部皮质骨内的最大应力值随着总厚度的减小而快速升高,当总厚度大于2.0 mm时,种植体颈部皮质骨内的最大应力值随着总厚度的增大而缓慢升高;③皮质骨在总厚度较小的时候,最大应力主要分布在种植体颈部和根部对应的骨面上;④应尽量保证皮质骨的厚度达到松质骨厚度的2倍以上,以避免应力集中导致骨吸收,造成种植失败。
本研究建立模型时,颌骨模型的建立均采用颊舌对称的形态,从而简化建模过程。同时,种植体尺寸化为圆柱体;骨皮质和骨松质的厚度参考文献[6],具有科学上的准确性。因此,各模型建立具有真实性。同时,模型建立中也进行了一些简化,将冠修复简化为长方体,颌力分解为垂直和水平方向的载荷。这些简化虽然可能对计算结果有一定的影响,但就本研究所探讨的中心问题而言,各项定性指标的结果是合理可信的。研究者[15]分析上颌窦提升术时发现:有螺纹的种植体与无螺纹种植体对应力分布的影响无明显差别,再次证明简化模型可以合理地使用。Qian等[16]使用由松质骨和皮质骨组成无解剖特征的简化颌骨模型,分析了种植体直径、植入深度和颌力方向变化对应力应变的影响,为临床提供了有价值的指导。研究[17]表明:应用简化的有限元模型,同样可以定性地揭示问题的本质,能为进一步评价及研究种植体系统提供基础理论支持。
国外学者Bougherara等[18]研究了种植体在皮质骨双层、皮质骨单层、无皮质骨3种类型中种植体骨界面应力分布情况。但在临床实践中,多数是由松质骨及单层皮质骨共同支持的设计种植,很少应用皮质骨双层及无皮质骨支持的种植体设计。研究[11]证实:应力集中部位为种植体颈部,该部位的应力集中导致种植体颈部的皮质骨吸收。而种植体颈部的皮质骨吸收是引起种植体出现松动,进而导致种植修复失败的重要因素。这也证明了本研究采用有限元分析种植体颈部应力分布的合理性。本研究结果表明:总厚度增大后,种植体及其周围骨组织内的应力集中明显降低,这与Motoyoshi等[19]在临床试验中发现种植体使用寿命随着皮质骨厚度的增大而增加的观察是一致的。
另外,在种植体周围的力学系统中,骨组织的几何因素对种植体系统的应力分布有着重要的影响[2, 5, 6, 7, 8]。
综上所述,本研究建立了简化的颌骨种植体模型,采用三维有限元分析了松质骨和皮质骨的厚度及其厚度比例对种植体周围应力分布的影响。本研究结果表明:种植体手术中应优先保证松质骨和皮质骨的总厚度大于或等于2.0 mm,且总厚度的最佳值为2.0 mm。本研究采用的2个几何参数,即松质骨和皮质骨的总厚度及其厚度比例观察种植体区域的应力分布,对后续的对种植体系统的研究有重要的启示意义。
| [1] | Hasan I,Bourauel C,Mundt T,et al.Biomechanics and load resistance of short dental implants:a review of the literature[J].ISRN Dent,2013,2013:1-5. |
| [2] | Chun HJ,Cheong SY,Han JH,et al.Evaluation of design parameters of osseo integrated dental implants using finite element analysis[J].J Oral Rehabil,2002,29(6):565-574. |
| [3] | 王煜婷,张少锋,董岩,等.All-on-4种植体参数对周围骨应力影响的三维有限元分析[J].实用口腔医学杂志,2014,30(2):193-197. |
| [4] | Alberius P,Gordh M,Lindberg L,et al.Influence of surrounding soft tissues on onlay bone graft incorporation[J].Oral SurgOral MedOral PatholOral RadiolEndod,1996,82(1):22-33. |
| [5] | Hansson S.A conical implant-abutment interface at the level of the marginal bone improves the distribution of stresses in the supporting bone.An axisymmetric finite element analysis[J].Clin Oral Implants Res,2003,14(3):286-293. |
| [6] | Kitamura E,Stegaroiu R,Nomura S,et al.Biomechanical aspects of marginal bone resorption around osseointegrated implants:considerations based on a three-dimensional finite element analysis[J].Clin Oral Implants Res,2004,15(4):401-412. |
| [7] | 姜琴,邓锋,王超,等.微种植体舌侧内收上前牙力系三维有限元非线性模型的建立[J].第三军医大学学报,2015,37(16):1652-1656. |
| [8] | 李英,鲍萍萍,孙雯,等.下颌第一磨牙种植冠减径后的三维有限元分析[J].现代口腔医学杂志,2015,29(4):205-208. |
| [9] | 赵刚,魏佳佳,张晓平,等.两种颌间牵引对下颌骨微种植体及周围影响的三维有限元分析[J].中国组织工程研究,2013,17(24):4444-4450. |
| [10] | Hasan I,Heinemann F,Reimann S,et al.Finite element investigation of implant-supported fixed partial prosthesis in the premaxilla in immediately loaded and osseointegrated states[J].Comput Methods Biomech Biomed Engin,2011,14(11):979-985. |
| [11] | 马莉莎,唐亮,潘燕环.双端种植固定桥修复前后种植体-骨界面的动力学研究[J].中华口腔医学杂志,2012,47(7):435-438. |
| [12] | 蔡留意,林久祥,张月兰,等.个体化舌侧矫治器微种植体支抗滑动法内收上前牙的三维有限元模型的构建[J].中华口腔正畸学杂志,2014,21(1):14-18. |
| [13] | Huang HL,Hsu JT,Fuh LJ,et al.Biomechanical simulation of various surface roughnesses and geometric designs on an immediately loaded dental implant[J].Comput Biol Med,2010,40(5):525-532. |
| [14] | Bashutski JD,D'Silva NJ,Wang HL.Implant compression necrosis:current understanding and case report[J].J Periodontol,2009,80(4):700-704. |
| [15] | Schuller-Götzburg P,Entacher K,Petutschnigg A,et al.Sinus elevation with a cortical bone graft block:a patient-specific three-dimensional finite element study[J].Int J Oral Maxillofac Implants,2011,27(2):359-368. |
| [16] | Qian L,Todo M,Matsushita Y,et al.Effects of implant diameter,insertion depth,and loading angle on stress/strain fields in implant/jawbone systems:finite element analysis[J].Int J Oral Maxillofac Implants,2008,24(5):877-886. |
| [17] | Clelland NL,Lee JK,Bimbenet OC,et al.A three-dimensional finite element stress analysis of angled abutments for an implant placed in the anterior maxilla[J].J Prosthodont,1995,4(2):95-100. |
| [18] | Bougherara H,Rahim E,Shah S,et al.A preliminary biomechanical assessment of a polymer composite hip implant using an infrared thermography technique validated by strain gage measurements[J].J Biomech Eng,2011,133(7):689-698. |
| [19] | Motoyoshi M,Inaba M,Ono A,et al.The effect of cortical bone thickness on the stability of orthodontic mini-implants and on the stress distribution in surrounding bone[J].Int J Oral Maxillofac Surg,2009,38(1):13-18. |
 2016, Vol. 42
2016, Vol. 42


