扩展功能
文章信息
- 王志坚, 李彦旭, 韩青, 尚晓峰, 王金成
- WANG Zhijian, LI Yanxu, HAN Qing, SHANG Xiaofeng, WANG Jincheng
- 髋关节置换术中2种不同髋关节假体的有限元分析:应力集中和位移变化比较
- Finite element analysis of two different hip prostheses in hip arthroplasty: Comparison of stress concentration and displacement
- 吉林大学学报(医学版), 2019, 45(02): 347-352
- Journal of Jilin University (Medicine Edition), 2019, 45(02): 347-352
- 10.13481/j.1671-587x.20190223
-
文章历史
- 收稿日期: 2018-06-24
2. 吉林大学第二医院骨科, 吉林 长春 130041
2. Department of Orthopaedics, Second Hospital, Jilin University, Changchun 130041, China
全髋关节置换术可以使髋关节疼痛、股骨头坏死导致的髋关节功能障碍和行动不便等症状得到缓解,现已广泛应用于骨科手术中。全世界每年已有50万例患者因髋关节障碍接受全髋关节置换术[1]。鉴于人体内部髋关节结构较复杂,导致在人体内进行生物力学实验不具备安全性和准确性,因此运用有限元方法对人体生物力学进行分析以解决上述难题。1958年有限元方法的概念首次被提出[2],目前这种技术已被普遍应用于骨科生物力学中[3]。1972年BREKELMANS等[4]和RYBICKI等[5]采用有限元方法对临床骨科工作进行模拟,为后续骨科工作奠定了基础。BELYTSCHKO等[6]和STOIK等[7]通过有限元分析方法模拟了全髋关节置换术下的4种骨水泥型植入物在正常循环步态和爬楼梯荷载过程中的机械损伤情况。LAVERNIA等[8]采用不同直径的股骨头3D模型对步态下人体单腿负载时的应力情况进行分析,通过绑定的接触方式得出最大主应力与头部直径的关系。
本研究通过对非均质材料属性的赋值,使现有研究方式中有限元软件上无法轻易做出非均质股骨柄分析结果的难题得以解决,从而使模拟情况更符合实际,计算结果更具有参考性。且现有研究中在设置不同表面的接触情况时往往进行简单的绑定操作,本研究通过面与面之间进行了相应的摩擦系数的设置,使得结果中的位移更具有参考价值,以期为临床中术前的规划、术中的假体选择和术后的随访复检及调治提供可靠的理论依据。
1 资料与方法 1.1 一般资料选用1名年龄54岁的健康男性志愿者,身高175cm,体质量70kg,采用CT机扫描成像技术进行扫描,CT数据出自吉林大学第二医院,取志愿者股骨髋关节处扫描数据,CT机扫描参数:扫描速度26mm·s-1,倾角0.842°,层厚1mm, 扫描电压120kV, 扫描电流340 mA, 扫描方式为螺旋扫描。
本研究模拟解剖型假体全髋关节置换,比较2种不同解剖型假体来对比分析置换后的应力和下沉位移情况。目前临床手术中普遍使用Corail与Synergy porous解剖型钛合金(Ti6Al4V)假体,这2种假体适用性较好,但术前为患者选取假体时无可靠理论依据,因此本研究通过有限元模拟对2种假体置换后的应力分布与相对位移下沉进行分析,以期为临床手术的术前规划提供可靠的理论参数。
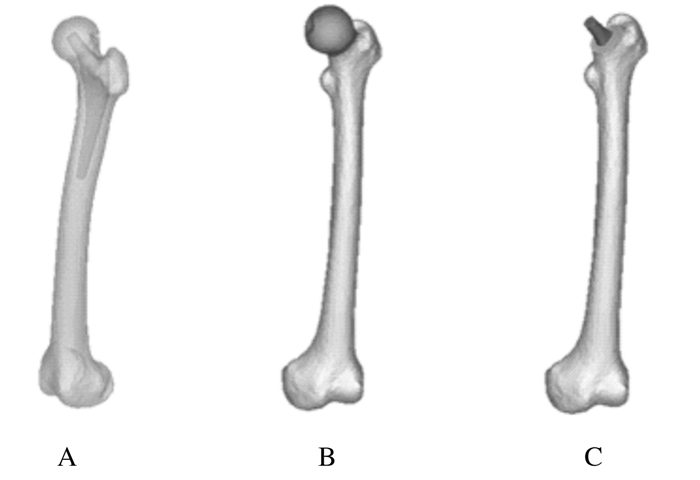
1.2 实体模型的建立对上述志愿者股骨中上段采用CT扫描,将扫描的CT图像进行阈值分割、等级设定和区域增长等图像处理操作,通过分离技术将志愿者股骨图像分离生成三维模型,将生成模型与植入假体模型进行布尔运算,模拟临床手术中器械扩髓过程和假体植入情况,根据临床及现有的研究方法[9]将股骨头切除露出假体便于与球头和髋臼配合。见图 1。
|
| A:Boolean operation; B:Split femur; C:Matching diagram. 图 1 股骨与假体压配示意图 Fig. 1 Schematic diagram of femoral and prosthetic compression |
|
|
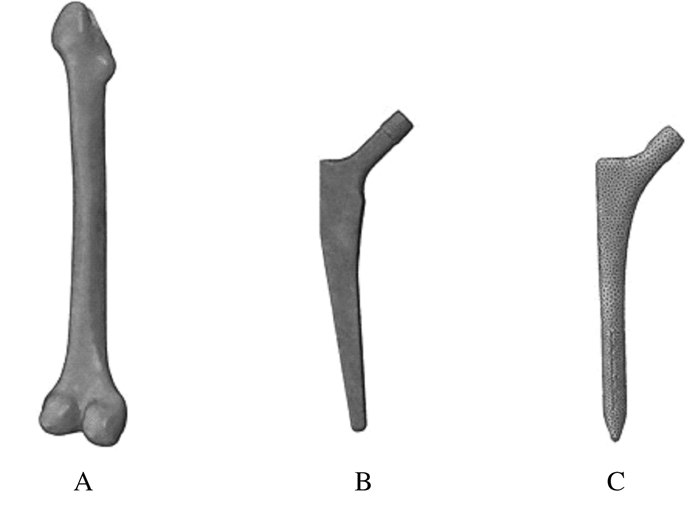
通过Hypermesh软件对股骨与假体模型进行3D单元网格划分,股骨模型由2 373 113个C3D4型四面体单元构成,Corail型假体由95 518个C3D4型四面体网格构成,Synergy porous型假体模型由109 472个C3D4型四面体单元构成。见图 2。
|
| A:Femoral mesh; B:Corail stem mesh; C:Synergy porous stem mesh. 图 2 置换网格模型 Fig. 2 Displacement mesh model |
|
|
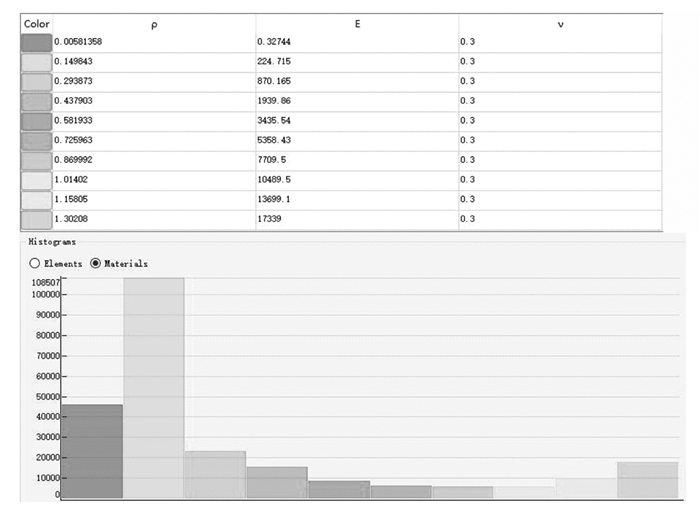
采用Mimics软件进行材料的非均质赋值,其原理是运用CT图像的阈值分割及区域增长等算法计算出灰度值(Hounsfield unit,HU),通过得到的HU值以及公式1可以将股骨三维模型中任意位置的密度及弹性模量等参数与不同的HU值一一对应,达到股骨模型非均质属性的建立,赋值情况见图 3。将假体柄在ABAQUS软件中进行均质属性赋值,取各向同性弹性体,弹性模量取110Gpa,泊松比(μ)为0.3[10]。公式1:ρ=0.04+0.0008×HU, E=10200 ρ2.01, μ=0.3;式中ρ为骨骼的密度,E为弹性模量。
|
| 图 3 非均质股骨材料参数 Fig. 3 Heterogeneous femur material parameters |
|
|
将股骨实体模型与假体模型分别导入ABAQUS软件中进行装配创建接触条件,由于假体与骨髓腔之间的配合较为复杂且在Mimics中已进行布尔运算,因此股骨与假体间为面与面接触合理性更高,在分析过程中比较全面。假体外表面与骨髓腔间设置摩擦系数为0.3,以贴合实际情况。
1.4 边界条件的建立股骨与假体配合的边界条件对有限元分析的精度有很大影响,因此对边界条件的设定应模拟真实情况,但边界条件的影响因素有很多,完全按照真实情况模拟几乎不可能,因此要适当地进行理想化处理。分析过程中将股骨远端完全固定,约束其全部6个自由度。
载荷的加载与边界条件同理,理想化模拟人体股骨的载荷情况,对假体上段加载人体以站立姿态静止时股骨所承受的集中力[11],空间力的大小可以简化为XYZ轴3个方向的轴向力,其大小分别为Fx=497N, Fy=-118N, Fz=-1575N。见图 4。

|
| 图 4 配合模型载荷示意图 Fig. 4 Diagram of matching model loading |
|
|
分析中根据股骨与假体的贴合情况,站立静止时可将髋关节处看作受到一个恒定的压力,因此在分析步中设定静力通用类型。由于实验模型较大,运算增量步数少易产生不收敛现象导致分析失败,故设置分析最大增量步数为1 000,使分析更全面化。完成前处理工作,分析计算。
2 结果 2.1 假体柄模拟Corail型假体的应力分布较Synergy porous型假体更为均匀且无过多的高应力集中点,2种假体与股骨接触拐角处及其远端1/3处为最大应力集中区,Corail型假体最大应力为31.82 MPa,Synergy porous型假体最大应力为38.95 MPa。假体柄Von Mises云图见图 5。

|
| A:Corail stem; B:Synergy porous stem. 图 5 假体柄Von Mises云图 Fig. 5 Von Mises cloud images of prosthesis stem |
|
|
2种模型下的股骨应力集中位置均为股骨远端1/3处与假体股骨接触位置,且Corail型假体股骨最大应力为31.82 MPa,Synergy porous型假体股骨最大应力较大, 为55.05 MPa。股骨Von Mises云图见图 6。

|
| A:Corail model femur; B:Synergy porous model femur. 图 6 股骨Von Mises云图 Fig. 6 Von Mises cloud images of femur |
|
|
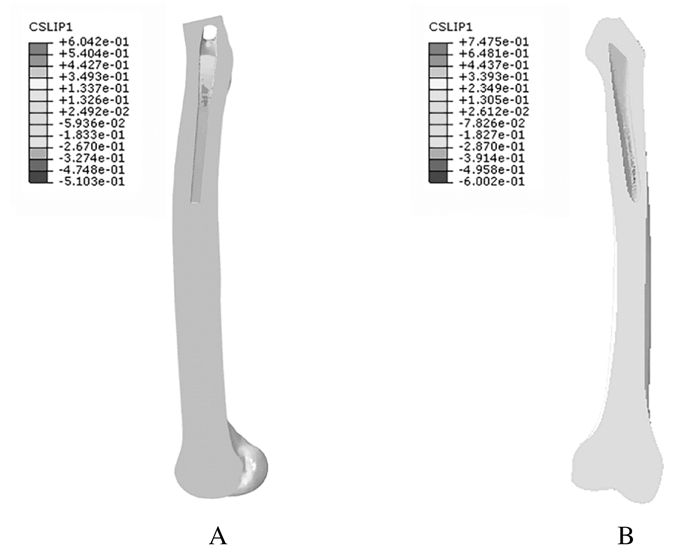
通过模型Cslip云图可得Corail型假体最大相对位移为0.604 mm,Synergy porous型假体最大相对位移为0.747 mm。2种模型间股骨内髓腔与假体外表面的相对位移大小见图 7。
|
| A:Corail model femur; B:Synergy porous model femur. 图 7 模型Cslip云图 Fig. 7 Cslip cloud images of model |
|
|
根据Dorr分型标准[12],本研究选用的股骨为标准B型股骨。在进行全髋关节置换术后假体柄与股骨髓腔内壁之间会产生一定范围的应力分布[13],并且假体柄在术后有下沉趋势[14]。在本研究中对周围骨质的分析,采用各向异性的非均质赋值,相对于将皮质骨与松质骨简化为各向同性的赋值更贴合实际[15],同时对于下沉趋势的分析,在髓腔与假体表面设置摩擦属性的面与面接触代替简单的绑定接触来分析下沉距离,使分析更全面可靠。应力的分布均匀与否体现了假体与股骨的受力是否均匀,应力的大小表明了在压配过程中假体柄对股骨的影响幅度,高应力集中点是影响局部骨裂和骨缺损的重要因素,过大会产生骨裂甚至骨折,过小会产生应力遮挡从而影响骨长入的情况[16],因此合理的应力分布是影响压配结果的重要因素。
从股骨应力方面考虑,骨骼材料屈服强度约为138MPa[17],2种假体模型下股骨应力均符合置换要求。在股骨应力分布中MATSUYAMA等[18]认为股骨远端1/3处应力分布最为明显,且高应力集中点较多。这些结果表明基于有限元方法这种应力分布可能更有助于在应力遮挡的影响下股骨的骨增长与长入。本研究中2种模型的股骨应力集中区均为股骨假体接触处与股骨远端1/3处,与临床术后结果相贴合,适宜骨长入,但术后由于股骨底端受力较多可能会对膝关节有一定损伤,因此要随访观察膝关节的术后情况。对于应力大小而言,Corail型假体股骨最大应力较Synergy porous型假体股骨更小,虽然2种假体均有防悬功能,但Corail型假体在轴向上有一定弯曲角度更易贴合骨髓腔,因此应力较小更适合置换,且二次伤害和翻修的概率更小,使用年限更长。
在假体柄应力的研究中,MOULGADA等[19]采用有限元方法对比分析2种假体Ceraver-Osteal与Charnley在不同载荷下的应力分布情况,结果表明:改良的Ceraver-Osteal假体相对于Charnley假体在骨髓腔内的剪切应力更小,使用年限更长。本研究中Corail型假体较Synergy porous型假体其应力分布更均匀,应力集中区较少,且2种假体与股骨接触拐角处及其远端1/3处为最大应力集中区,会产生假体发热以及磨损,最后导致假体与股骨配合不紧密发生错位。同时Corail型假体最大应力较Synergy porous型假体更小更易满足屈服要求,对股骨内髓腔的伤害较小,不易产生裂隙甚至断裂等情况,更满足全髋关节置换术的术后要求。
全髋关节置换后,由于人体轴向负载作用下,假体会产生一定的下沉现象,MANN等[20]运用有限元方法和生物力学实验分析人体上下楼时植入体与骨髓腔贴合处的间隙大小对迁移的影响,发现2种模型在相对位移<1 mm内,均不会产生术后股骨干松动等现象。AMIROUCHE等[1]利用有限元骨骼-肌肉模型分析在步态条件下股骨假体微动情况与股骨下沉位移的关联,表明无其他条件干扰下股骨偏移在2 mm之内,骨植入物微动和应力峰值无改变。本研究中通过Cslip云图可以看出2种假体相对位移大小分别为0.604和0.747 mm,均满足置换要求,植入假体后不会产生过大的晃动,但Corail型假体最大相对位移更小,可能由于Corail型假体轴向有一定锥度,与骨髓腔配合会产生一定的支持导致置换后假体下沉位移更小,因此较Synergy porous型假体更不易产生松动、晃动和磨损等现象,对股骨伤害更小、翻修概率更小。
在临床中对于标准型的股骨,Corail型假体与Synergy porous型假体相比,不论是应力分布、应力大小和相对位移Corail型假体均具有一定优势,通过有限元方法分析假体置换装配过程得到的应力分布结果和下沉位移分析可为临床骨科手术医生提供合理的理论参考依据,为临床医生手术制定提供准确的参数。
综上所述,本研究采用非均质有限元股骨模型与假体柄进行摩擦属性下的压配建模,更符合实际情况。从应力方面考虑,Corail型假体与股骨最大应力较Synergy porous型更小,在满足应力遮挡的条件下,Corail型假体与股骨应力分布更平均,高应力集中区较少,更符合全髋关节置换的条件。从相对位移方面考虑,Corail型假体最大相对位移较Synergy porous型假体更小,置换后假体下沉位移更小,不易产生松动、下沉和磨损等现象。因此在临床手术中对于标准B型股骨,不同类型假体的有限元分析可为髋关节置换术的预后效果评价提供重要参考。
| [1] | AMIROUCHE F, SOLITRO G, WALIA A. No effect of femoral offset on bone implant micromotion in an experimental model[J]. Orthopaed Traumatol Surg Res, 2016, 102(3): 379–385. |
| [2] | ANDRESS H J, KAHL S, KRANZ C, et al. Clinical and finite element analysis of a modular femoral prosthesis consisting of a head and stem component in the treatment of pertrochanteric fractures[J]. J Orthopaed Trauma, 2000, 14(8): 533–546. |
| [3] | HUISKES R, CHAO E Y. A survey of finite element analysis in orthopedic biomechanics:the first decade[J]. J Biomech, 1983, 16(6): 385–409. |
| [4] | BREKELMANS W A M, POORT H W, SLOOFF T J J H. A new method to analyse the mechanical behaviour of skeletal parts[J]. Acta Orthop Scand, 1972, 43(5): 301–317. |
| [5] | RYBICKI E F, SIMONENF A, WEIS E B Jr. On the mathematical analysis of stress in the human femur[J]. J Biomechanics, 1972, 5(2): 203–215. |
| [6] | BELYSCHKO T, KULAK R F, SCHULTZ A B, et al. Finite element stress analysis of an intervertebral disc[J]. J Biomech, 1974, 7(3): 277–285. |
| [7] | STOLK J, JANSSEN D, HUIKES R, et al. Finite element-based preclinical testing of cemented total hip implants[J]. Clin Orthop Relat Res, 2007, 456: 138–147. |
| [8] | LAVERNIA C J, LACOBELLI D A, VILLA J M, et al. Trunnion-head stresses in THA:Are big heads trouble?[J]. J Arthroplasty, 2015, 30(6): 1085–1088. |
| [9] | PENG J Q, CHEN HY, HU Y, et al. Finite Element Analysis of porously punched prosthetic short stem virtually designed for simulative uncemented hip arthroplasty[J]. BMC Musculoskelet Dis, 2017, 18(1): 295. |
| [10] | TANG F, ZHOU Y, ZHANG W, et al. All-polyethylene tibial components in distal femur limb-salvage surgery:a finite element analysis based on promising clinical outcomes[J]. J Orthop Surg Res, 2017, 12(1): 57. |
| [11] | CELIK T, MUTLU I, OZKAN A, et al. Comparison of the lag screw placements for the treatment of dtable and unstable intertrochanteric femoral fractures regarding trabecular bone failure[J]. J Med Eng, 2016, 2016(9): 5470798. |
| [12] | KENDOFF D O, CITAK M, EGIDY C C, et al. Eleven-year results of the anatomic coated CFP stem in primary total hip arthroplasty[J]. J Arthroplasty, 2013, 28(6): 1047–1051. |
| [13] | OH Y, FUJITA K, WAKABAYASHI Y, et al. Location of atypical femoral fracture can be determined by tensile stress distribution influenced by femoral bowing and neck-shaft angle:a CT-based nonlinear finite element analysis model for the assessment of femoral shaft loading stress[J]. J Injury-Int Care Injured, 2017, 48(2): 2736–2743. |
| [14] | LAURENCE M. Computer methods in biomechanics and biomedical engineering[J]. J Bone Joint Surg, 1998, 13(4): 1–3. |
| [15] | PÉTURSSON P, EDMUNDS K J, GÍSLASON M K, et al. Bone mineral density and fracture risk assessment to optimize prosthesis selection in total hip replacement[J]. Computat Math Methods Med, 2015, 2015: 162481. |
| [16] | FAISAL T R, LUO Y H. Study of stress variations in single-stance and sideways fall using image-based finite element analysis[J]. Biomed Mater Eng, 2016, 27(1): 1–14. |
| [17] | 王以进. 骨科生物力学[M]. 北京: 人民军医出版社,1989. |
| [18] | MATSUYAMA K, ISHIDOU Y, GUO Y M, et al. Finite element analysis of cementless femoral stems based on mid-and long-term radiological evaluation[J]. BMC Musculoskelet Disord, 2016, 17(1): 397. |
| [19] | MOULGADA A, BOUZIANE M M, BOUIADJRA B B, et al. Finite element simulation of stress distribution in the different components of Ceraver-Osteal hip prosthesis:Static and dynamic analysis[J]. Mechanika, 2014, 20(5). DOI:10.5755/jol.mech.20.5.5372 |
| [20] | MANN K A, DAMRON L A, MILLER M A, et al. Stem-cement porosity may explain early loosening of cemented femoral hip components:experimental-computational in vitro study[J]. J Orthop Res, 2007, 25(3): 340–350. |
 2019, Vol. 45
2019, Vol. 45


