扩展功能
文章信息
- 贾一凡, 胡敏
- JIA Yifan, HU Min
- “2×4”矫治系统中前倾弯弓丝弯折位置变化对其力学行为影响的三维有限元分析
- Effect of variation of bending location of tip-forward bending arch wires on its mechanical behavior in "2×4" appliance system: A three-dimensional finite element analysis
- 吉林大学学报(医学版), 2018, 44(06): 1249-1255
- Journal of Jilin University (Medicine Edition), 2018, 44(06): 1249-1255
- 10.13481/j.1671-587x.20180624
-
文章历史
- 收稿日期: 2018-04-08
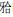 的纠正。结论:
三维空间"2×4"矫治系统中,前倾弯弓丝弯折位置的变化将影响整个力学系统的表达;磨牙前倾弯弓丝对矫治前牙开
的纠正。结论:
三维空间"2×4"矫治系统中,前倾弯弓丝弯折位置的变化将影响整个力学系统的表达;磨牙前倾弯弓丝对矫治前牙开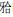 不利,临床使用时要结合辅助措施。
不利,临床使用时要结合辅助措施。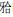 前倾弯 有限元分析 生物力学
前倾弯 有限元分析 生物力学 前牙开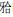
Burstone等[4]证实了二维空间内两托槽系统中,V形曲位置变化能够改变整个力学系统。可以设想,三维空间内V形曲(前倾弯或后倾弯)位置的改变也会影响三维空间内的力学系统。但先前的研究多关注两颗牙齿在垂直方向上的受力情况,该受力系统既与临床中多颗牙力学系统有所不同,又欠缺对其他方向上牙齿的受力和力矩的分析,也有临床医师[5]认为三维空间内V形曲力学系统与二维空间内的研究结果不同。目前对三维空间内弓丝弯折位置变化如何影响其力学作用的研究很少,这给临床应用前倾弯矫治前牙开
选取1例减数双侧上颌第一前磨牙的成年女性患者,其牙体和牙周组织健康,无全身系统性疾病或颌骨外伤史,充分排齐整平上颌牙列后,行锥形束CT(CBCT)扫描(患者知情同意),以DICOM格式保存,导入Mimics软件,在相应的灰度阈值下,建立上颌骨和上颌牙齿的masks层,Erase命令去除下颌骨、部分上颌骨及头颅固定支架等干扰信息,采用Draw命令对颌骨以及牙列的空隙区域进行填充,得到所需要的上颌骨及上颌牙列的断层图。运用Calculate 3D命令生成包含上颌骨以及上颌牙列的初步三维模型,导入逆向工程软件Geomagic Studio,采用网格医生命令进行表面的精修细化。使用Offset指令将上颌牙齿外表面向外围均匀扩展0.20 mm,得到牙周膜的前体模型,采用布尔运算得出牙周膜模型。使用偏移命令将牙槽骨内移1.5 mm,并保留原先的牙槽骨,再采用减操作,得到厚度为1.5 mm的皮质骨,内部则认为是松质骨,使用曲面功能获得曲面模型。
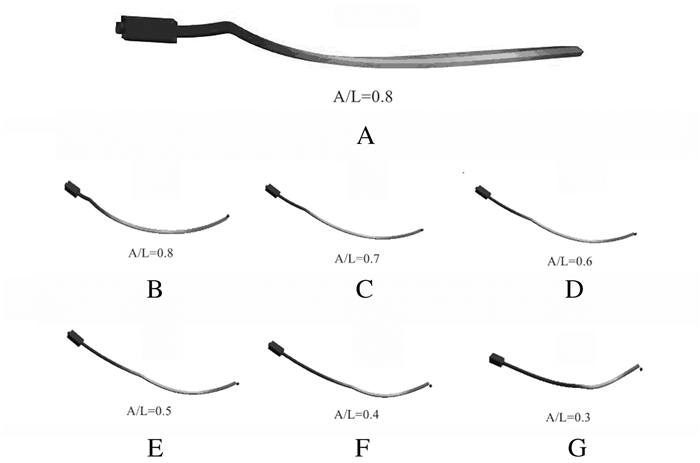
参考中切牙、侧切牙和第一磨牙的MBT托槽数据,利用三维机械制图软件UG绘制托槽的草图,布尔命令得到托槽的实体模型。根据临床冠中心位置初步定位托槽位置,移动托槽模型使之与牙齿保持临床中实际关系,采用曲线命令建立从一侧第一磨牙至对侧第一磨牙的路径,绘制出弓丝截面的曲线草图,尺寸为0.017英寸×0.025英寸(0.43 mm×0.64 mm),材质为β钛,结合OPA-K弓形做细微调整,得到平直弓丝的模型。参考平直弓丝的形态,绘制前倾弯弓丝,弓丝弯折高度统一设定为弯折点至弓丝平面的距离5 mm。定义L为一侧第一磨牙颊管中心点至中切牙托槽中心点的弓丝长度,A为弓丝弯折点至中切牙托槽中心点的弓丝长度,结合临床实际,共有6种不同的前倾弯弓丝形态及相应的三维模型,A/L分别为0.8、0.7、0.6、0.5、0.4和0.3。见图 1。
|
| A: Lateral view of 0.8 location; B-G: Lateral-superior views of 0.8, 0.7, 0.6, 0.5, 0.4, and 0.3 locations (right-half of archwires). 图 1 前倾弯弓丝模型 Figure 1 Tip-forward bend archwire models |
|
|
将构建好的上颌骨、上颌牙列、牙周膜、托槽和不同前倾弯弓丝的三维模型均导入至UG软件中进行组装和精细调整,并设置坐标系,以上颌第二磨牙舌尖连线中点为原点,设定X、Y和Z坐标轴方向,分别代表水平向、矢状向垂直向,其中患者的左侧定义为X轴正方向,患者的后方定义为Y轴正方向,患者的上方定义为Z轴正方向,从而建立包含上颌牙列和直丝弓托槽(MBT托槽)的“2×4”矫治系统的三维实体模型。见图 2(插页五)。

|
| 图 2 包含上颌牙列和托槽的“2×4”矫治系统的三维实体模型(面观) Figure 2 Stereo-model of "2×4" appliance system including maxillary dentition and brackets (occlusal view) |
|
|
将上述实体模型导入有限元分析专用软件Ansys workbench 15中,并对该模型进行边界约束、接触类型定义、材料属性赋予、网格划分,得到包含上颌牙列和MBT托槽的“2×4”矫治系统的三维有限元模型。
1.2 边界约束和接触定义在上颌骨的周围实行固定约束,设定X、Y和Z三个方向上的位移和旋转均为0,保证在施加矫治力时上颌骨不发生变形。定义弓丝在受力状态下为非线性几何大变形,其余材料在受力状态下为线性刚性小变形。托槽和牙齿、牙齿和牙周膜、牙周膜和皮质骨、皮质骨和松质骨的接触关系为bonded类型。牙齿和托槽无相对运动,托槽的槽沟和弓丝的接触关系为no separation类型,允许弓丝在托槽槽沟内滑动,但是垂直向上不发生分离,摩擦系数为0.15。
1.3 材料属性和网格划分根据材料不同的属性,模型主要包括皮质骨、松质骨、牙周膜、牙齿、弓丝和托槽6种材料属性。为简化实验,减小计算量,6种材料均设定为均质的、各向同性的线弹性体。各材料的具体力学参数参考相关文献[9-10],见表 1。模型的网格划分采用四面体十节点单元,节点数为172 338,网格数为92 704,见图 3(插页五)。
| Material | Young’s Modulus (P/MPa) |
Poisson’s ratio |
| Cortical bone | 13 700 | 0.30 |
| Cancellous bone | 1 370 | 0.30 |
| Tooth | 19 600 | 0.30 |
| Bracket | 200 000 | 0.30 |
| Periodontal ligament | 0.13 | 0.45 |
| TMA wire | 69 000 | 0.30 |

|
| A:HBsAg; B: HBeAg; C: HBcAg. 图 3 包含上颌牙列和托槽的“2×4”矫治系统的三维有限元模型(面观) Figure 3 Three-dimensional finite element model of "2×4" appliance system including maxillary dentition and brackets (occlusal view) |
|
|
根据不同的前倾弯弓丝形态,设计6种不同的工况,工况1~6的A/L分别为0.8、0.7、0.6、0.5、0.4和0.3。由于弓丝、托槽、牙列和颌骨左右基本对称,为简化实验和降低计算量,虽然两侧同时加力,但只对右侧进行分析。基于梁理论,使用Ansys workbench 15软件计算不同工况下弓丝对中切牙、侧切牙和第一磨牙托槽的作用力和力矩,并进行载荷的加载。
2 结果 2.1 中切牙、侧切牙和第一磨牙的受力情况表 2中Total一栏代表牙齿所受力或力矩的数值大小,不含方向。切牙、侧切牙和第一磨牙所受力和力矩见表 2。
| Code | Axis | Central incisor | Lateral incisor | First molar | |||||
| Force(N) | Moment(N·mm) | Force(N) | Moment(N·mm) | Force(N) | Moment(N·mm) | ||||
| 1 | X | 9.462 178 176 e-011 | -7.495 446 566 | 2.506 478 271 e-010 | -5.001 571 474 | -0.168 922 916 8 | 19.958 938 7 | ||
| Y | -1.302 607 452 e-009 | 1.486 597 913 | -3.450 532 346 e-009 | 2.701 458 502 | 0.178 853 234 9 | 11.942 144 46 | |||
| Z | -0.325 896 887 1 | -8.118 171 149 e009 | -0.863 282 146 6 | -1.224 988 178 e-008 | 1.178 607 449 | 3.350 032 993 | |||
| Total | 0.325 896 887 1 | 7.641 445 712 | 0.863 282 146 6 | 5.684 504 837 | 1.204 009 531 | 23.498 867 41 | |||
| 2 | X | 2.135 240 023 e-010 | -4.851 283 256 | 8.479 859 74 e-011 | -1.811 232 984 | 4.813 709 547 e-002 | 10.304 958 33 | ||
| Y | -2.215 936 101 e-009 | 0.944 778 326 6 | -8.800 329 215 e-010 | 0.927 390 755 7 | 0.130 860 944 9 | 7.084 838 349 | |||
| Z | -0.408 634 709 3 | -7.658 268 408 e009 | -0.162 284 470 1 | -5.975 460 488 e-009 | 0.552 405 407 | -0.878 777 649 | |||
| Total | 0.408 634 709 3 | 4.942 424 032 | 0.162 284 470 1 | 2.034 850 986 | 0.569 731 077 3 | 12.536 321 26 | |||
| 3 | X | 7.043 810 448 e-010 | -4.831 968 271 | -4.478 601 708 e-010 | -0.263 20 4679 7 | 2.598 840 655 e-002 | 6.189 836 006 | ||
| Y | -6.450 975 365 e-009 | 0.942 084 165 7 | 4.101 664 675 e-009 | 0.133 916 817 5 | 7.698 315 766 e-002 | 4.835 027 925 | |||
| Z | -0.908 511 830 4 | -1.043 564 632 e008 | 0.577 650 798 1 | -1.154 955 152 e-009 | 0.303 301 214 3 | -0.529 308 673 2 | |||
| Total | 0.908 511 830 4 | 4.922 950 33 | 0.577 650 798 1 | 0.295 314 099 6 | 0.313 995 908 4 | 7.872 212 68 | |||
| 4 | X | 1.765 859 934 e-009 | -4.983 157 038 | -1.552 188 454 e-009 | 0.830 217 983 4 | -4.065 551 766 e-004 | 3.437 095 036 | ||
| Y | -1.737 897 215 e-009 | 0.974 384 148 7 | 1.527 609 372 e-009 | -0.417 310 442 4 | 3.371 412 087 e-002 | 3.439 613 22 | |||
| Z | -1.325 379 417 | -7.916 930 583 e009 | 1.165 006 717 | 1.653 331 375 e-009 | 0.138 820 510 9 | -0.168 833 253 3 | |||
| Total | 1.325 379 417 | 5.077 526 813 | 1.165 006 717 | 0.929 198 528 4 | 0.142 856 366 6 | 4.865 497 514 | |||
| 5 | X | -2.206 601 256 e-010 | -5.645 099 182 | 2.218 357 859 e-010 | 2.180 027 209 | -3.925 388 343 e-002 | 0.742 151 7062 | ||
| Y | -1.170 674 12 e-008 | 1.103 008 584 | 1.176 911 524 e-008 | -1.061 490 325 | -3.066 440 339 e-003 | 2.311 022 268 | |||
| Z | -1.984 862 156 | -5.877 984 03 e009 | 1.995 437 555 | 6.018 326 032 e-009 | -3.362 991 205 e-002 | 0.380 166 052 1 | |||
| Total | 1.984 862 156 | 5.751 849 504 | 1.995 437 555 | 2.424 722 735 | 5.178 070 495 e-002 | 2.456 855 572 | |||
| 6 | X | 2.979 566 836 e-009 | -6.610 463 883 | -3.207 068 923 e-009 | 4.536 851 071 | -0.151 980 923 2 | -3.121 535 755 | ||
| Y | 4.841 570 977 e-009 | 1.249 316 956 | -5.211 244 658 e-009 | -1.986 965 658 | -1.024 623 049 e-003 | 0.903 894 527 2 | |||
| Z | -3.261 387 873 | -4.184 617 951 e009 | 3.510 408 153 | 1.195 140 185 e-009 | -0.310 214 800 9 | 1.987 346 731 | |||
| Total | 3.261 387 873 | 6.727 482 858 | 3.510 408 153 | 4.952 883 015 | 0.345 445 326 | 3.809 272 61 | |||
分析中切牙、侧切牙及第一磨牙在Z轴方向上的受力,以及X轴方向上所受力矩,将不同工况下中切牙、侧切牙及第一磨牙所受的FZ及MX制成点线图,见图 4和5。

|
| 图 4 Z轴方向上各牙齿所受力 Figure 4 Forces of teeth on Z ax |
|
|

|
| 图 5 X轴方向各牙齿所受力矩 Figure 5 Moments of teeth on X axis |
|
|
在前倾弯的各工况下,随着弯折部位自靠近第一磨牙的位置向靠近侧切牙的位置逐渐移动可见:①第一磨牙由A/L为0.8位置的压低力逐渐减小,至约0.41位置降为0N,进而变为伸长力并逐渐增大;力矩由A/L为0.8位置的前倾力矩逐渐减小,至约A/L为0.38位置降为0 N·mm,进而变为后倾力矩并逐渐增大;②侧切牙由A/L为0.8位置的伸长力逐渐减小,至约A/L为0.68位置降为0N,进而变为压低力并逐渐增大;力矩由A/L为0.8位置的舌倾力矩逐渐减小,至约A/L为0.59位置降为0 N·mm,进而变为唇倾力矩并逐渐增大;③中切牙始终受伸长力,由A/L为0.8位置至A/L为0.3位置逐渐增大;力矩始终为舌倾力矩,由A/L为0.8位置逐渐减小,至约A/L为0.6位置,又开始缓慢增大;④2颗切牙所受合力由A/L为0.8位置的伸长力逐渐减小,至约A/L为0.41的位置降为0N,进而变为压低力并逐渐增大,整个过程与第一磨牙垂直方向上受力基本平衡;合力矩始终为舌倾力矩,由A/L为0.8位置至A/L为0.3位置逐渐减小。
2.3 中切牙、侧切牙和第一磨牙其他方向上的受力和受力矩情况在前倾弯的各工况下,受力和受力矩有以下特点:①右侧中切牙从A/L为0.8位置到A/L为0.3位置,在X轴、Y轴方向上,受力很小,在Z轴方向上受力矩很小;在Y轴方向上,所受力矩为顺时针方向(患者正面观);②右侧侧切牙从A/L为0.8位置到A/L为0.3位置,在X和Y轴方向上,受力很小,在Z轴方向上受力矩很小;在Y轴方向上,所受力矩从A/L为0.8位置时的顺时针(患者正面观),逐渐减小,到A/L为0.5位置已变为逆时针(患者正面观),随后大小逐渐增大;③右侧第一磨牙从A/L为0.8位置到A/L为0.3位置,在Y轴方向上所受力矩始终为逆时针方向(患者正面观),并逐渐减小。
2.4 中切牙、侧切牙和第一磨牙位移趋势以中切牙、侧切牙切缘中点,第一磨牙近颊尖、近舌尖、远颊尖和远舌尖4个牙尖顶点为牙冠参考点,以中切牙、侧切牙根尖点,第一磨牙近颊根、远颊根和腭侧根3个根尖点为牙根参考点,X轴代表近远中向(近中为正),Y轴代表颊舌向(舌侧为正),Z轴代表垂直向(上方为正),描述前倾弯位于A/L为0.8位置(工况1)时,中切牙、侧切牙和第一磨牙的牙冠位移趋势。见表 3和4。
| (1×10-2mm) | ||||||
| Axis | Central incisormidpoint of incisor edge | Lateral incisormidpoint of incisor edge | First molar | |||
| Mesial-buccal cuspid | Mesial-lingual cuspid | Distal-buccal cuspid | Distal-lingual cuspid | |||
| X | -1.911 024 239 | -6.606 320 577 | 23.776 991 360 | 22.205 595 670 | 22.803 957 410 | 22.413 313 530 |
| Y | 30.369 605 340 | 25.729 464 140 | -6.979 539 730 | -7.578 732 706 | -4.390 352 990 | -4.928 100 351 |
| Z | -6.333 166 309 | -4.500 035 100 | 6.385 126 999 | 10.333 926 960 | -4.019 027 181 | -1.334 811 950 |
| Total | 31.081 729 970 | 26.942 514 960 | 25.589 629 530 | 25.638 169 100 | 23.567 949 690 | 22.987 486 150 |
| (1×10-2mm) | |||||
| Axis | Central incisorroot apex | Lateral incisor root apex | First molar | ||
| Palatal root apex | Mesial-buccalroot apex | Distal-buccalroot apex | |||
| X | 0.618 361 025 1 | 2.306 081 230 | -10.660 435 770 | -10.583 258 820 | -9.695 561 478 |
| Y | -14.601 442 3500 | -13.421 232 310 | 1.904 671 237 | -0.186 540 412 | 1.603 988 042 |
| Z | -2.499 437 3640 | -1.102 391 175 | -2.406 879 813 | 6.598 794 990 | -1.928 575 365 |
| Total | 31.081 729 9700 | 13.662 457 820 | 11.093 499 620 | 12.473 341 970 | 10.014 793 710 |
二维空间内弓丝对托槽的力学行为可以从两个方面来描述:①2个非共线托槽与平直弓丝组成的力学系统受两槽沟成角大小的影响,其中槽沟与平直弓丝成角较大的托槽主导力学系统的方向;②2个共线托槽与V形曲弓丝组成的力学系统受弯折位置变化的影响,其中距离V形曲较近的托槽主导力学系统的方向。Burstone等[4]测定了V形曲位置变化过程中2个托槽受力与受力矩的变化,当V形曲位于2个托槽中点(A/L=0.5)时,2个托槽均不受力(托槽槽沟近远中边缘受到1对大小相等、方向相反的力,即力偶),只受到大小相等、方向相反的力矩作用,这点亦被称作“中性点”;当V型曲位于三分点(A/L=0.33、0.67)时,距离V形曲较远的托槽只受到力的作用,受力矩为0,并随着V形曲继续远离发生力矩反转,即力矩方向与距离V形曲较近的托槽一致。但二维空间内弓丝力学行为的研究只能描述2个托槽在单一平面内的受力和受力矩情况,对临床应用的指导意义有限。
三维空间内2颗第一磨牙托槽和2颗中切牙托槽组成的“2×2”矫治系统,可以近似看作两托槽系统在三维空间的对应。Isaacson等[11]通过构建三维空间内的“2×2”矫治系统有限元模型发现:该力学系统中力的中性点变为V形曲距离第一磨牙的弓丝长度占弓丝长度的约45%(A/L=0.55)时,力矩反转点为V形曲距离第一磨牙的弓丝长度占弓丝长度的约14%(A/L=0.86)和63%(A/L=0.37),均与二维空间内两托槽系统不同。胡敏等[12]采用离体牙进行CT扫描,通过建立类似“2×2”矫治系统的有限元模型,分析了前倾弯对第一磨牙和中切牙牙周膜应力的作用,对临床应用作出了指导。
但上述对三维空间内矫治力学系统的研究存在以下局限性:首先,建模方法多采用磨片切片法、三维测量法或CT扫描图像处理法。磨片切片法采用破坏性建模,过程不可逆,方法复杂,主观性大,费时费力,且因切口损耗、工具定位和截面图像处理等因素造成误差较大;三维测量法需专用设备进行数据采集,数据转换后才能用于建模,且只能得到表面数据,无法得到内在的组织结构,不能反映组织本身材料性质;CT图像处理法需要将CT原始数据转换为图文,易造成数据的流失和失真,需要按扫描次序和层厚在每张图片中自行定义三维坐标轴,降低了精度。随着三维有限元建模方法的发展,逆向工程建模法因直接读取CT输出的原始数据,免除了繁琐的数据采集和处理,建模速度快,减少了数据多次转换后造成的信息丢失,可信度较高,且模型可以重复使用,成为了目前主流的建模方法。其次,既往研究的关注点仅为2颗牙齿在垂直方向上的受力和前后方向的力矩,对其他方向上的受力和受力矩并未进行探讨。临床上常运用的是由2颗第一磨牙和4颗切牙粘接托槽组成的“2×4”系统,因左右两侧各有3个托槽同时参与力学系统的构成,其受力和力矩更加复杂,且与三维“2×2”系统有所不同。本实验结合临床实际设置前倾弯弓丝弯折位置,分析中切牙、侧切牙与第一磨牙3颗牙齿在垂直方向上的受力和前后方向的力矩,结果显示:对于3颗牙齿来说,不存在1个力的中性点,让所有牙齿的受力同时为0N,但在0.41位置,第一磨牙垂直方向受力为0N,中切牙和侧切牙所受合力为0N。同时,并非所有牙齿均发生力和力矩反转,中切牙作为距离弯折处最远的牙,在整个过程中一直受伸长力作用,未发生力矩反转,而侧切牙的力矩反转点在A/L为0.59位置,第一磨牙的力矩反转点在A/L为0.38位置。三维空间内“2×4”系统受力与受力矩情况与二维空间两托槽系统、三维空间“2×2”系统不同的原因包括:三维空间内前倾弯不只造成弓丝弯折的形变,还有前牙段弓丝入槽时发生的扭矩形变;牙齿不仅沿受力方向平动,还将发生扭转等其他平面上的运动;侧切牙距离弯折处更近,分担了中切牙的部分力和力矩。对于前牙牙性开
对于典型的磨牙前倾弯弓丝,弯折位置在A/L约为0.8位置,此时中切牙和侧切牙受到伸长力和舌倾力矩,垂直方向上的位移趋势为伸长;第一磨牙虽然受压低力,但受到的前倾力矩较大,位移趋势提示,虽然近中颊尖、近中舌尖压低,但牙冠近中倾斜、舌倾,远中颊尖、舌尖伸长,同时牙弓宽度扩宽。该力学系统中,第一磨牙的前倾不利于近中倾斜牙轴的纠正,临床上应利用片段弓,将前磨牙纳入支抗单位,减小其不利作用。
综上所述,本实验利用逆向工程法建立包含上颌牙列和直丝弓托槽的“2×4”矫治系统的三维有限元模型,对前倾弯弓丝弯折位置变化时其力学行为的变化进行了系统研究,分析了磨牙前倾弯作用下各牙齿位移趋势,以期为临床应用前倾弯弓丝起到指导作用。
| [1] | Ramos-Jorge J, Motta T, Marques LS, et al. Association between anterior open bite and impact on quality of life of preschool children[J]. Braz Oral Res, 2015, 29: 46. |
| [2] | Perazzo MF, Gomes MC, Neves T, et al. Oral problems and quality of life of preschool children:self-reports of children and perception of parents/caregivers[J]. Eur J Oral Sci, 2017, 125(4): 272–279. DOI:10.1111/eos.2017.125.issue-4 |
| [3] | Guilherme Janson FV. Open-bite malocclusion:treatment and stability[M]. Iowa: Wiley Blackwell Publishing, 2014: 129-141. |
| [4] | Burstone CJ, Koenig HA. Creative wire bending——the force system from step and V bends[J]. Am J Orthod Dentofacial Orthop, 1988, 93(1): 59–67. DOI:10.1016/0889-5406(88)90194-1 |
| [5] | Nasiopoulos AT, Taft L, Greenberg SN. A cephalometric study of Class Ⅱ, division 1 treatment using differential torque mechanics[J]. Am J Orthod Dentofacial Orthop, 1992, 101(3): 276–280. DOI:10.1016/0889-5406(92)70097-T |
| [6] | Ryu WK, Park JH, Tai K, et al. Prediction of optimal bending angles of a running loop to achieve bodily protraction of a molar using the finite element method[J]. Korean J Orthod, 2018, 48(1): 3–10. DOI:10.4041/kjod.2018.48.1.3 |
| [7] | Heidary Z, Mojra A, Shirazi M, et al. A novel approach for early evaluation of orthodontic process by a numerical thermomechanical analysis[J]. Int J Numer Method Biomed Eng, 2018, 34(1). |
| [8] | 王芳, 胡敏, 李洪, 等. 种植体支抗辅助快速扩大上颌的三维有限元分析[J]. 吉林大学学报:医学版, 2010, 36(4): 745–748. |
| [9] | Kojima Y, Fukui H. Numerical simulations of canine retraction with T-loop springs based on the updated moment-to-force ratio[J]. Eur J Orthod, 2012, 34(1): 10–18. DOI:10.1093/ejo/cjq164 |
| [10] | Magesh V, Harikrishnan P, Kingsly Jeba Singh D. Finite element analysis of slot wall deformation in stainless steel and titanium orthodontic brackets during simulated palatal root torque[J]. Am J Orthod Dentofacial Orthop, 2018, 153(4): 481–488. DOI:10.1016/j.ajodo.2017.08.011 |
| [11] | Isacson RJ, Lindauer SJ, Conley P. Responses of 3-dimensional arch wires to vertical v-bends:comparisons with existing 2-dimensional data in the lateral view[J]. Semin Orthod, 1995, 1(1): 57–63. DOI:10.1016/S1073-8746(95)80090-5 |
| [12] |
胡敏, 刘磊.
应用前倾弯弓丝治疗开 畸形的生物力学研究[J]. 中华口腔医学杂志, 2004, 39(3): 233–235.
DOI:10.3760/j.issn:1002-0098.2004.03.017 畸形的生物力学研究[J]. 中华口腔医学杂志, 2004, 39(3): 233–235.
DOI:10.3760/j.issn:1002-0098.2004.03.017 |
| [13] |
胡敏, 张丽雯.
摇椅形弓丝配合前牙区垂直牵引矫治开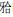 时牙齿应力分布与位移趋势的研究[J]. 实用口腔医学杂志, 2008, 24(1): 45–48.
DOI:10.3969/j.issn.1001-3733.2008.01.011 时牙齿应力分布与位移趋势的研究[J]. 实用口腔医学杂志, 2008, 24(1): 45–48.
DOI:10.3969/j.issn.1001-3733.2008.01.011 |
| [14] | Janson G, Rizzo M, Laranjeira V, et al. Posterior teeth angulation in non-extraction and extraction treatment of anterior open-bite patients[J]. Prog Orthod, 2017, 18(1): 13. DOI:10.1186/s40510-017-0167-z |
| [15] | Buschang PH, Carrillo R, Rossouw PE. Orthopedic correction of growing hyperdivergent, retrognathic patients with miniscrew implants[J]. J Oral Maxillofac Surg, 2011, 69(3): 754–762. DOI:10.1016/j.joms.2010.11.013 |
| [16] | Xun C, Zeng X, Wang X. Microscrew anchorage in skeletal anterior open-bite treatment[J]. Angle Orthod, 2007, 77(1): 47–56. DOI:10.2319/010906-14R.1 |
| [17] | Alsafadi AS, Alabdullah MM, Saltaji H, et al. Effect of molar intrusion with temporary anchorage devices in patients with anterior open bite:a systematic review[J]. Prog Orthod, 2016, 17: 9. DOI:10.1186/s40510-016-0122-4 |
| [18] | Marzouk ES, Kassem HE. Long-term stability of soft tissue changes in anterior open bite adults treated with zygomatic miniplate-anchored maxillary posterior intrusion[J]. Angle Orthod, 2018, 88(2): 163–170. DOI:10.2319/072317-490.1 |
| [19] | Baek MS, Choi YJ, Yu HS, et al. Long-term stability of anterior open-bite treatment by intrusion of maxillary posterior teeth[J]. Am J Orthod Dentofacial Orthop, 2010, 138(4): 391–396. |
| [20] | Choi YJ, Kim DJ, Nam J, et al. Cephalometric configuration of the occlusal plane in patients with anterior open bite[J]. Am J Orthod Dentofacial Orthop, 2016, 149(3): 391–400. DOI:10.1016/j.ajodo.2015.08.020 |
| [21] | Janson G, Laranjeira V, Rizzo M, et al. Posterior tooth angulations in patients with anterior open bite and normal occlusion[J]. Am J Orthod Dentofacial Orthop, 2016, 150(1): 71–77. DOI:10.1016/j.ajodo.2015.12.016 |
| [22] | 胡敏, 刘磊, 张丽雯, 等. 多曲方丝弓配合前牙区垂直牵引下颌牙齿移动趋势的光弹性研究[J]. 华西口腔医学杂志, 2007(5): 493–496. DOI:10.3321/j.issn:1000-1182.2007.05.022 |
| [23] | Freitas BV, Abas FMC, Dias L, et al. Nonsurgical correction of a severe anterior open bite with mandibular molar intrusion using mini-implants and the multiloop edgewise archwire technique[J]. Am J Orthod Dentofacial Orthop, 2018, 153(4): 577–587. DOI:10.1016/j.ajodo.2016.12.032 |
| [24] | 林娟颖, 刘晓颖, 吕建成, 等. 上颌第二磨牙生物力学有限元分析[J]. 中国医学物理学杂志, 2017, 34(8): 832–836. DOI:10.3969/j.issn.1005-202X.2017.08.016 |
 2018, Vol. 44
2018, Vol. 44


