2. 中国石油大学(华东)地球科学与技术学院, 山东 青岛 266580
2. School of Geosciences, China University of Petroleum, Qingdao 266580, Shandong, China
0 引言
阵列感应测井作为一种重要的电阻率测井方法,其优点是分辨率高、对侵入现象反映明显、探测深度深、测量信息丰富,对地层及储层流体评价具有重要的作用[1-4]。阵列感应测井响应与仪器线圈系结构和地层的电阻率直接相关,相同地层条件下不同结构的线圈系测井响应不同,地层电阻率同样影响测井响应。地层电阻率不仅与地层岩性有关,还与地层孔隙度、渗透率、地下水矿化度及地层温度等因素有关;温度又决定了地下水的矿化浓度,所以地层温度是影响地层电阻率的重要参数。温度升高使地下水密度和黏滞性减小,溶解能力增强,水矿化度随之增高,离子活性增加,从而电阻率降低[5]。
稠油是世界经济发展的重要资源,我国对稠油油藏的研究、开发和加工已日趋成熟,并已形成相当大的开采规模。开采稠油通常采用的是注热法,其中以注蒸汽法应用最为广泛[6]。高温媒介的注入使得地层温度升高,热量在地层中传导影响了地层的电阻率,也影响了阵列感应测井的响应。众多学者利用多种方法[7-8]对地层中的热传导进行了研究,主要包括有限差分法、有限体积法和有限元法;其中有限元法具有网格剖分和边界条件上的优势,因此该方法被广泛应用到多种物理场的仿真中。近年来,多名学者利用有限元数值模拟方法[9]对阵列感应测井进行了数值模拟研究,分析了多种地层条件和影响因素下的测井响应[10-16];但对于热采过程地层温度对阵列感应测井响应的影响研究较少。
本文通过有限元法模拟阵列感应测井在不同井下地层温度的响应,研究温度对阵列感应测井响应直接的影响,以阐释稠油热采地层阵列感应测井出现的异常现象。
1 热采地层模型与数值模拟方法利用二维轴对称的有限元法模拟阵列感应测井在不同地层温度条件下的响应。首先需要分别建立均质地层模型与热采地层模型,热采地层模型由目的层和上、下围岩三层组成,又可称为三层阶跃地层。图 1a为均质地层模型,在模拟过程中地层外侧温度变化,井眼温度为常温,地层的原始电阻率为定值;图 1b为热采过程的基本地层模型,即三层阶跃地层模型,井眼温度为常温,目的层温度变化,研究目的层温度升高对阵列感应测井响应的影响。地层中的热传递主要表现为多孔介质中的热传导和孔隙流体的热对流[17],根据能量守恒定律,多孔介质的热传导微分控制方程表示为:
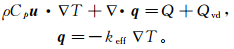 (1)
(1)

|
| a.均质地层模型;b.三层阶跃地层模型。 图 1 地层模型示意图 Figure 1 Stratigraphic model |
|
|
式中:ρ为密度(kg/m3);Cp为恒压下的比热容(J/kg·K);u速度矢量(m/s);∇为矢量微分运算符;T为固体温度(K);q为导电热通量(W/m2);Q为单位体积产生的热(W/m3);Qvd为热黏性消散(W/m3);-keff为有效导热系数(W/(m·K))。
边值条件如下:在地层远端满足第一类边界条件,
 (2)
(2) 在热绝缘处满足第二类边界条件,
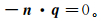 (3)
(3) 式中,n边界处的法向矢量。给定目的层边界的温度:
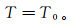 (4)
(4) 地层电阻率与地层温度密切相关。本文通过有限元数值模拟方法模拟地层的热传导,确定地层中温度场的分布,进而确定地层电阻率。前苏联科学家Γ.Α.切列缅斯基早在20世纪70年代就通过大量的实验总结出岩层电阻率与岩层温度之间的关系[5]:
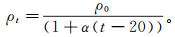 (5)
(5) 式中:ρ0为岩层温度为20 ℃时的电阻率,可以近似认为是岩层的基本电阻率;ρt为岩层温度为t(℃)时的电阻率,是勘察测量得到的电阻率;α为岩石温度系数。一般情况下,α=0.02,t=T-273.15。本文根据公式(5)将温度的模拟与地层电阻率结合,通过有限元方法模拟阵列感应测井响应,不对温度场响应进行具体的研究。采用的仪器为Baker Atlas公司的高分辨率感应测井仪器HDIL,其线圈半径近似为0.03 m,远小于波长和线圈间距,可以将发射电流源等效为磁偶极子源[18]。HDIL仪器有8个工作频率,7个子阵列,从子阵列1到子阵列7的线圈系长度逐渐增大[19],本文研究仪器频率为20 kHz时仪器各子阵列的测井响应。
在柱坐标系中,电磁场A(r, z)满足偏微分方程:
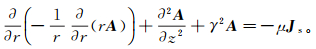 (6)
(6) 式中:γ为传播系数;Js为集中在发射线圈内的电流密度(A/m2);μ为磁导率(H/m);A为磁矢势(Wb/m)。
边值条件如下:在地层远端满足第一类边界条件,
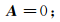 (7)
(7) 在磁绝缘处满足第二类边界条件,
 (8)
(8) 均质地层模型是研究稠油热采过程阵列感应测井响应的基础。均质地层模型中考虑地层电阻率随温度发生变化,设置井眼,但井眼中泥浆电阻率始终与地层电阻率相同,即不考虑泥浆电阻率对阵列感应测井视电阻率响应的影响,在该模型中阵列感应测井响应仅受到温度的影响。
建立如图 1a所示的均质地层模型,模拟井眼半径为0.1 m,地层半径为30 m,地层厚度为60 m,原始地层电阻率Rt分别为1, 5, 10, 20, 50, 100 Ω·m,地层温度为300~600 K的测井响应。模拟结果如图 2所示。
|
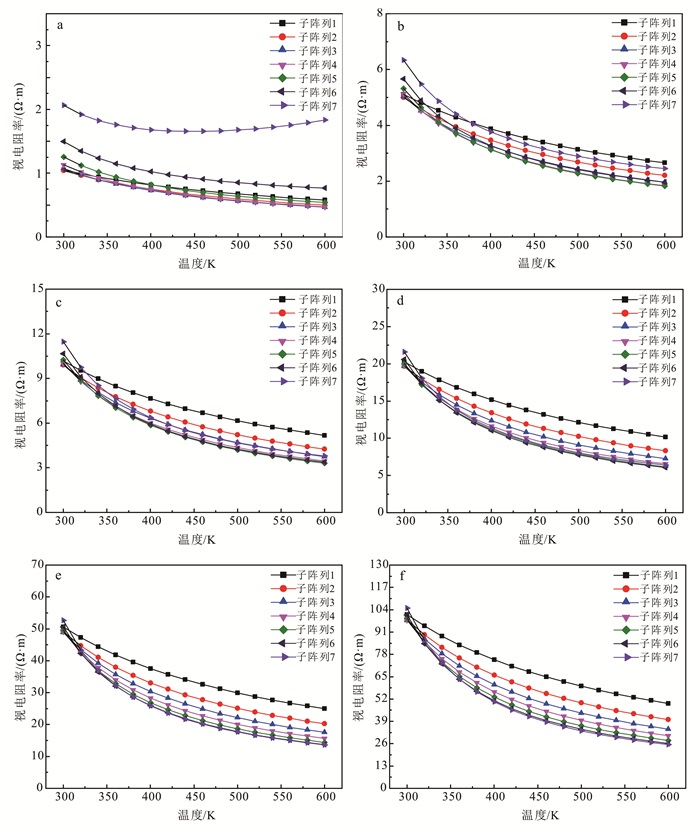
| a.Rt=1 Ω·m;b.Rt=5 Ω·m;c.Rt=10 Ω·m;d.Rt=20 Ω·m;e.Rt=50 Ω·m;f.Rt=100 Ω·m。 图 2 均质地层中温度变化视电阻率响应 Figure 2 Apparent resistivity response of temperature changes in homogeneous formation |
|
|
由图 2可得到以下结论:
1) 图 2a中子阵列7的视电阻率在温度达到400 K时出现了上升趋势,并不是因为地层电阻率随地层温度的升高而增大了,而是由于子阵列7的线圈系结构过长,电流的趋肤效应严重,导致其在低电阻率条件下会发生失真的情况;因此,子阵列7不能正确测量低阻地层的视电阻率。
2) 阵列感应测井各个子阵列视电阻率随温度的升高而下降,且不同阵列的下降速度不同,从子阵列7到子阵列1下降速度依次减小。
3) 视电阻率随温度下降的趋势逐渐减缓,在300~400 K内下降速度较快,400 K之后下降速度逐渐减慢。
3 三层阶跃地层模型温度影响分析多层阶跃地层是阵列感应测井过程中遇到的主要地层,而在稠油热采的过程中,三层阶跃地层是其基本单位,因此研究稠油热采地层中三层阶跃地层模型的温度影响是进一步研究复杂地层的基础[18]。下面对三层阶跃地层模型中温度影响阵列感应测井常见的3种情况进行讨论:目的层及围岩电阻率变化、目的层温度变化及目的层厚度变化。
三层阶跃地层模型主要模拟热采过程中目的层温度上升导致测井响应的异常。高温媒介使得目的层的温度升高,建立如图 1b所示模型,地层模型宽度为30 m,高度为50 m,井眼半径为0.1 m,阵列感应测井仪器在井眼中移动,测量地层的视电阻率。
3.1 目的层及围岩电阻率的影响地层电阻率是影响阵列感应测井响应的直接因素。令目的层温度T=400 K,目的层厚度H=4 m,围岩电阻率Rs=5, 10 Ω·m,Rt=10, 20, 30 Ω·m,研究目的层及围岩电阻率对阵列感应测井响应的影响,模拟结果见图 3。

|
| a.Rt=10 Ω·m,Rs=5 Ω·m;b.Rt=10 Ω·m,Rs=10 Ω·m;c.Rt=20 Ω·m,Rs=5 Ω·m;d.Rt=20 Ω·m,Rs=10 Ω·m;e.Rt=30 Ω·m,Rs=5 Ω·m;f.Rt=30 Ω·m,Rs=10 Ω·m。 图 3 目的层及围岩电阻率变化视电阻率响应 Figure 3 Apparent resistivity response of target and surrounding formation resistivity changes |
|
|
由图 3可得到以下结论:
1) 视电阻率曲线的最低点总是出现在目的层的两侧或目的层中点位置。当目的层视电阻率大于围岩视电阻率时,视电阻率曲线最低点出现在围岩两侧;当目的层视电阻率等于围岩电阻率时,视电阻率曲线最低点出现在目的层中点位置。
2) 目的层电阻率增大,其各子阵列的目的层视电阻率增大,且长阵列的视电阻率逐渐小于短阵列的视电阻率;围岩电阻率增大,其各子阵列的围岩视电阻率增大,长阵列的视电阻率逐渐小于短阵列的视电阻率。
3) 从目的层边界处到围岩地层较远处,阵列感应测井子阵列视电阻率逐渐增大,并且短阵列与长阵列的视电阻率差值逐渐减小。
3.2 目的层温度的影响目的层温度变化会影响目层的电阻率,同时也会影响阵列感应测井的响应。令H=4 m,Rs=5 Ω·m,Rt=20 Ω·m,T=300, 400, 500, 600 K,研究三层阶跃地层模型目的层温度对阵列感应测井响应的影响,模拟结果如图 4所示。

|
| a.T=300 K;b.T=400 K;c.T=500 K;d.T=600 K。 图 4 目的层温度变化视电阻率响应 Figure 4 Apparent resistivity response of target formation temperature |
|
|
由图 4可得到结论:
1) 目的层温度升高对视电阻率减小的影响程度逐渐减弱,温度由300 K升高为400 K时,其视电阻率变化程度较大。
2) 目的层为300 K(近似于常温)时,短阵列视电阻率值大于长阵列视电阻率值;随着目的层温度的升高,短阵列的视电阻率值相比于长阵列逐渐减小;当地层温度达到600 K时,短阵列视电阻率值小于长阵列视电阻率值。
3) 目的层温度升高,围岩视电阻率曲线分离程度增大,从目的层到围岩远处视电阻率增大的趋势变大。
3.3 目的层厚度的影响目的层厚度的变化可以使围岩及不同子阵列的测井响应发生变化,令T=400 K,Rs=5 Ω·m,Rt=20 Ω·m,H分别为4, 3, 2, 1 m,研究在相同温度下目的层厚度对阵列感应测井响应的影响,其模拟结果如图 5所示。
|
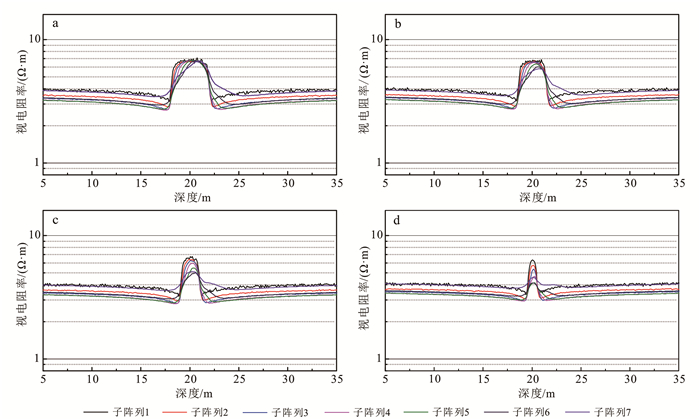
| a.H=4 m;b.H=3 m;c.H=2 m;d.H=1 m。 图 5 目的层厚度变化视电阻率响应 Figure 5 Apparent resistivity response of target formation thickness changes |
|
|
由图 5可以得到结论:
1) HDIL阵列感应测井仪器子阵列1到子阵列7探测深度逐渐增加,围岩对相应子阵列的影响程度也就越大,因此长阵列对目的层厚度变化更为敏感,短阵列对目的层厚度的变化敏感性相对较差。由于围岩电阻率小于目的层电阻率,当目的层厚度减小时,长阵列视电阻率减小的速度与幅度较大,在一定范围内厚度的变化甚至对短阵列没有影响,当目的层厚度小于1 m时所有阵列视电阻率下降。
2) 随着目的层厚度的减小,围岩视电导率曲线更加平直,由目的层到围岩远处视电阻率增大的趋势减缓。
3) 子阵列1视电阻率最低点均出现在目的层边界处,因此可以利用子阵列1视电阻率曲线的两个低值点所在位置确定目的层厚度。
通过以上对三层阶跃模型不同影响因素进行模拟得出的规律,可以利用阵列感应测井的视电阻率曲线判断目的层是否存在异常高温的现象,判断目的层的厚度,估算地层的电阻率,并对消除温度的影响提供一定的指导。
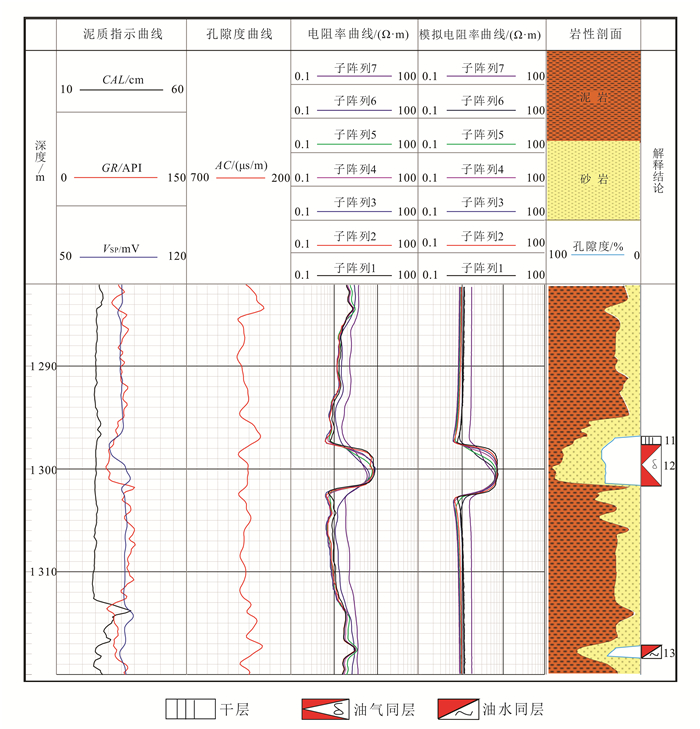
4 热采地层实例为了验证本文的研究方法对热采地层解释及识别的有效性,对G1井实际地层进行分析。利用本文模拟结果分析热采地层参数并建立相应模型,对比模拟结果与实际测井曲线。G1井为稠油热采区调整井,其钻探目的是为了完善某区蒸汽驱注采井网,增加储量动用程度;因此在测井时已通过井网注入高温蒸汽,目的层与蒸汽具有相近的温度。其阵列感应测井为其裸眼井阶段进行,测井解释成果图如图 6所示。
|
| CAL.井径;GR.自然伽马;VSP.自然电位;AC.声波时差。 图 6 G1井测井解释成果图 Figure 6 Log interpretation graph of well G1 |
|
|
井中1 297.5~1 302.3 m为稠油层,该井井网中注入蒸汽温度为623 K。通过不同子阵列的电阻率曲线可知围岩电阻率为2 Ω·m;根据图 5得出的结论,由电阻率曲线最低点位置判断地层厚度为4.9 m;通过目的层中点位置的视电阻率值及图 1结论,利用差值的方法确定地层电阻率为55 Ω·m。根据以上参数建立地层模型,利用有限元方法模拟热采地层的测井响应,模拟结果见图 6第四道。
对比模拟结果与实际测井曲线,模拟视电阻率曲线能够较好地吻合实际测井曲线;但由于实际地层复杂且在纵向上存在非均质性,模拟的视电阻率曲线很难与实际测井曲线完全一致。该方法能够较好地判断热采地层受温度影响后视电阻率的变化,可以判断地层电阻率和目的层厚度等,对实际解释现场测井异常特征、提供现场指导具有一定的意义。
5 结论1) 部分子阵列在低阻地层高温条件下出现失真的现象,不能有效测量地层地电阻率,这与子阵列的线圈系结构有关。
2) 温度影响各子阵列的视电阻率响应,随着温度升高各子阵列的视电阻率值降低,其中300~400 K温度范围内视电阻率下降速度较快,通过视电阻率下降的规律可判断地层原始电阻率。
3) 三层阶跃地层中,当目的层厚度减小时,长阵列视电阻率减小的速度与幅度较大,在一定厚度范围内对短阵列没有影响,因此可以通过短阵列视电阻率曲线最低点的位置确地层厚度。
4) 在三层阶跃地层中,视电阻率曲线的最低点总是出现在目的层边界或者目的层中点位置处,且由最低电阻率点向围岩地层较远处逐渐增大,其增大的趋势主要与目的层的温度与厚度有关:目的层温度升高,围岩视电阻率曲线分离程度增大,从目的层边界到围岩远处视电阻率增大的趋势变大;目的层温度减小,围岩视电导率曲线更加平直,由目的层到围岩远处视电阻率增大的趋势减小,且各子阵列的视电阻率差值逐渐减小。通过该规律可判断地层的异常高温影响。
5) 分析实际地层的测井响应,利用本文研究内容可以直接判断地层的厚度及地层原始电阻率。通过对实际地层进行模拟比对,验证了该模拟结果的准确性以及实用性,可对热采现场测井解释确定地层电阻率及地层厚度等参数提供一定的指导。
| [1] |
刘丹. 高分辨率阵列感应测井在苏里格致密砂岩储层评价中的应用[D]. 长春: 吉林大学, 2016.
Liu Dan. Application of HDIL in the Evaluation of Tight Sandstone Reservoirs in Sulige Area[D]. Changchun: Jilin University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10183-1016091778.htm |
| [2] |
李萌. 用阵列感应测井评价地层压力[D]. 荆州: 长江大学, 2016.
Li Meng. Research on Prediction Method of Formation Pressure from Array Induction Logs[D]. Jingzhou: Yangtze University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10489-1016237062.htm |
| [3] |
周峰, 孟庆鑫, 胡祥云, 等. 利用阵列感应测井进行储层渗透率评价[J].
地球物理学报, 2016, 59(11): 4360-4371.
Zhou Feng, Meng Qingxin, Hu Xiangyun, et al. Evaluation of Reservoir Permeability Using Array Induction Logging[J]. Chinese Journal of Geophysics, 2016, 59(11): 4360-4371. DOI:10.6038/cjg20161135 |
| [4] |
李波. 应用阵列感应资料识别油水层[J].
当代化工研究, 2017, 26(3): 34-35.
Li Bo. Application of Multi-Array Induction Data in the Recognition of Oil-Water Layer[J]. Modern Chemical Research, 2017, 26(3): 34-35. |
| [5] |
杜炳锐. 电法在深部地热勘查中的应用研究[D]. 成都: 成都理工大学, 2011.
Du Bingrui. The Study of Electrical Prospecting in the Deep Geothermal Investigation[D]. Chengdu: Chengdu University of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10616-1011235616.htm |
| [6] |
耿娜娜. 稠油热采井高温防砂技术研究[D]. 青岛: 中国石油大学(华东), 2007.
Geng Nana. The Technique of Sand Control for Heavy Oil Well at High Temperature[D]. Qingdao: China University of Petroleum. 2007. http://cdmd.cnki.com.cn/Article/CDMD-10425-2007226689.htm |
| [7] |
郭宽良.
数值计算传热学[M]. 合肥: 安徽科学技术出版社, 1987.
Guo Kuanliang. Numerical Computation Heat Transfer[M]. Hefei: Anhui Science and Technology Publishing House, 1987. |
| [8] |
施天谟.
计算传热学[M]. 北京: 科学出版社, 1987.
Shi Tianmo. Calculate Heat Transfer[M]. Beijing: Science Press, 1987. |
| [9] |
李大潜.
有限元素法在电法测井中的应用[M]. 北京: 石油工业出版社, 1980.
Li Daqian. Application of Finite Element Method in Electrical Logging[M]. Beijing: Petroleum Industry Press, 1980. |
| [10] |
邓少贵, 李智强, 范宜仁, 等. 斜井泥浆侵入仿真及其阵列侧向测井响应数值模拟[J].
地球物理学报, 2010, 53(4): 994-1000.
Deng Shaogui, Li Zhiqiang, Fan Yiren, et al. Numerical Simulation of Mud Invasion and Its Array Laterolog Response in Deviated Wells[J]. Chinese Journal of Geophys, 2010, 53(4): 994-1000. |
| [11] |
邓少贵, 莫宣学, 卢春利, 等. 缝-洞型地层缝洞的双侧向测井响应数值模拟[J].
石油勘探与开发, 2012, 39(6): 706-712.
Deng Shaogui, Mo Xuanxue, Lu Chunli, et al. Numerical Simulation of the Dual Laterolog Response to Fractures and Caves in Fractured Cavernous Formation[J]. Petroleum Exploration and Development, 2012, 39(6): 706-712. |
| [12] |
仵杰, 李宇腾, 付晨东, 等. 钻遇断层水平井地层模型的阵列感应测井响应特性数值模拟[J].
测井技术, 2017, 41(3): 266-271.
Wu Jie, Li Yuteng, Fu Chendong, et al. Numerical Simulation of Response Characteristics to the Array Indication Logging in the Horizontal Well Penetrating Faults[J]. Well Logging Technology, 2017, 41(3): 266-271. |
| [13] |
仵杰, 史盼盼, 陈延军, 等. 阵列感应测井在斜井和水平井中的响应特性[J].
测井技术, 2016, 40(2): 152-160.
Wu Jie, Shi Panpan, Chen Yanjun, et al. Response Characteristics of Array Induction Logging in Deviated and Horizontal Well[J]. Well Logging Technology, 2016, 40(2): 152-160. |
| [14] |
王昌学, 储昭坦, 肖承文, 等. 井环境对阵列感应测井响应的影响分析[J].
地球物理学报, 2013, 56(4): 1392-1403.
Wang Changxue, Chu Zhaotan, Xiao Chengwen, et al. The Analysis of Effect of the Borehole Environment on Response of Array Induction Logging[J]. Chinese Journal of Geophys, 2013, 56(4): 1392-1403. DOI:10.6038/cjg20130433 |
| [15] |
王钰楠, 关静. 阵列感应测井在直井和斜井中的对比[J].
计算机时代, 2017(2): 55-56.
Wang Yunan, Guan Jing. Comparison of Array Induction Logging in Vertical Well and Deviated Well[J]. Computer Era, 2017(2): 55-56. |
| [16] |
姜艳娇, 孙建孟, 高建申, 等. 低孔渗储层井周油藏侵入模拟及阵列感应电阻率校正方法[J].
吉林大学学报(地球科学版), 2017, 47(1): 265-278.
Jiang Yanjiao, Sun Jianmeng, Gao Jianshen, et al. Numerical Simulation of Mud Invasion Around the Borehole in Low Permeability Reservoir and a Method for Array Induction Log Resistivity Correction[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(1): 265-278. |
| [17] |
陈刚. 碳酸盐岩储层温度特征及温度测井资料应用研究[D]. 长春: 吉林大学, 2013.
Chen Gang. The Research of Temperature Characteristics in Carbonate Reservoirs and Temperature Logging Data Application[D]. Changchun: Jilin University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10183-1013193920.htm |
| [18] |
周新刚. 基于有限元法的水平井阵列感应测井响应数值计算研究[D]. 西安: 西安石油大学, 2012.
Zhou Xingang. Numerical Simulation of Responses of Array Induction Loggong in Horizontal Wells Based on the FEM[D]. Xi'an: Xi'an Shiyou University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10705-1013156639.htm |
| [19] |
张建华, 刘振华, 仵杰.
电法测井原理与应用[M]. 西安: 西北大学出版社, 2002.
Zhang Jianhua, Liu Zhenhua, Wu Jie. Principle and Application of Electrical Well Logging[M]. Xi'an: Northwest University Press, 2002. |


