2. 中国石化石油工程技术研究院, 北京 100101
2. Sinopec Research Institute of Petroleum Engineering, Beijing 100101, China
0 引言
地层压裂过程中通常有两种破裂类型,一种是张破裂,另一种是剪破裂[1-3]。张破裂是在地层存在裂缝或微裂缝的情况下,当外加应力超过地层临界应力强度因子时所产生的破裂;而剪破裂主要与地层的内摩擦角、内聚强度和地层应力相关。目前地层破裂模型主要指地层的张破裂;剪破裂是地层压裂过程中出现的一种重要破裂类型,但该破裂类型难以用微地震监测方法检测,而且利用测井资料研究剪破裂的文献和研究内容都较少。
谢海峰等[4]采用剪切盒物理模拟实验方法研究了脆性岩石的高温剪切性能,实验表明:胶结物材料和岩石内部微裂纹两种因素共同影响着岩石的性质和剪破裂,前者占主导地位;岩石断口面上具有多而密的平行线条纹和较多的岩屑等典型剪切破坏特征,表明岩石破坏为剪切断裂。李守定等[5]利用分形理论和数值模拟方法研究了岩石拉剪-压剪全区破裂准则以及剪切速率对岩石拉剪破裂强度的影响,研究结果表明岩石的微观断裂形式是拉伸破坏和剪切破坏的结合,剪破裂首先发生,剪切速率与剪切强度呈非线性负相关关系。吴子科[6]通过对地应力下Lyapunov指数的分析,认为破裂裂纹尖端破裂状态是混沌的,并利用Kolmogorov熵定量地评价了破裂裂纹尖端的混沌程度。牛虎林等[7]利用成像测井和地震资料相结合的统计分析方法,综合预测了裂缝发育带,有效评价了钻井诱导缝的方位和数量。周祥[8]对泥质体积分数分别为4%、15%、24%、31%的4组砂岩进行了三轴压缩试验,结果表明内摩擦角和黏聚力随含泥量的增加而逐渐减小。
本文利用电成像、偶极子声波和伽马等测井资料建立地层发生剪破裂的临界剪应力模型,当地层中的剪应力大于该临界剪应力时将发生剪破裂。此方法有利于判断地层压裂过程中出现剪破裂的条件和难易程度,估计剪破裂裂缝,优化压裂施工参数,降低地层的勘探开发成本,提高油气层的开发效率。
1 FMI测井资料识别剪切裂缝FMI(地层微电阻率扫描成像)测井是评价复杂矿物、地层构造和裂缝分布的一种常用方法[9]。它根据电阻率图像的纵向和横向变化,反映井壁周围的岩性、物性及井壁结构(裂缝、节理、层理、井壁破损、结核和断层等)等变化情况。钻井过程中,在钻头的正前方会产生张破裂缝,而在井眼周围由于受地应力作用和泥浆重力及钻具的作用力而产生钻井诱导缝。根据库仑破裂准则,该钻井诱导缝为剪破裂缝,利用FMI资料能有效识别地层在钻井过程中形成的诱导缝。
FMI测井在识别地层天然微裂缝和钻井诱导缝方面发挥了重要的作用[10-11]。FMI测井通过测量异常电流的变化情况识别地层可能存在的微裂缝,不同的裂缝宽度将导致不同的电导率异常面积,利用异常面积与地层电阻率和泥浆电阻率的关系可以进行裂缝宽度的定量评价[12-14]。利用FMI测井能有效识别层理缝和诱导缝(图 1)。层理缝通常是在沉积过程中产生的,大部分呈水平层理方向。由于受到地层中地应力各向异性和钻井泥浆的影响,在钻井过程中易产生一组与之相关的诱导缝;诱导缝在垂直井FMI图上应为一组平行且呈180°对称的高角度裂缝或雁列式裂缝。井壁崩落在FMI图像上表现为两条180°对称的垂直长条暗带或暗块。
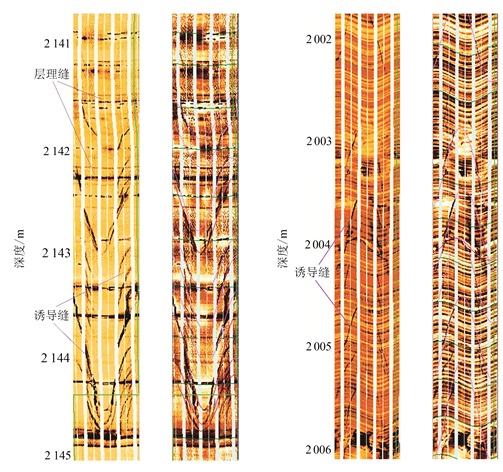
|
| 图 1 利用FMI测井资料识别层理缝和诱导缝 Figure 1 Identification bedding fractures and induced fractures using FMI logging data |
|
|
钻井诱导缝大部分是在钻铤震动和钻井液柱压力与地应力不平衡等条件下产生的,该裂缝满足库仑破裂准则。根据库仑准则给出的假设条件,地层在正应力σ的作用下,产生一定的剪应力τ,并满足
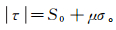 (1)
(1) 式中:S0为地层的内聚强度;μ是地层的内摩擦系数,μ=tan φ,φ是地层的内摩擦角。
从公式(1)发现,钻井过程中地层产生剪切力的大小取决于3个变量:钻井的正应力、地层的内聚强度和内摩擦系数。地层的内聚强度和内摩擦系数与岩石性质有关;钻井的正应力包含钻杆的重力、泥浆滤液的重力和钻井过程中的作用力之和,该正应力越大,则地层产生的剪切力越大。
地层存在水平方向的最大、最小地应力。钻井过程中,当钻井方向的正应力足够大,大于地层的破裂压力时会产生剪破裂,表现在最大水平地应力方向出现诱导裂缝。当钻井方向的正应力比较小,小于地层的坍塌压力时会出现坍塌,井壁地层坍塌的方位为最小水平地应力方向。
在地层二维条件下,正应力和剪应力表示为
在地层二维条件下,正应力和剪应力表示为
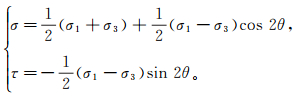 (2)
(2) 式中:σ1、σ3为子午面中的最大、最小水平地应力;θ为剪破裂面与σ3方向的夹角。
结合公式(1)和(2),得到地层内聚强度与应力之间的关系:
 (3)
(3) 为了获得地层发生剪破裂的临界条件,对公式(3)求极值,即
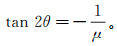 (4)
(4) S0是地层固有的性质,在钻井过程中出现诱导缝由三应力大小决定,因此利用钻井诱导缝可以确定地层的内聚强度S0。把公式(4)代入(3),得到在当前地应力时地层发生剪破裂的理论内聚强度为
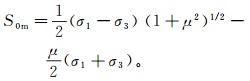 (5)
(5) 进一步整理公式(5),可以得到地层发生剪破裂的条件:
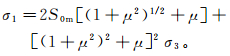 (6)
(6) 将公式(6)代入公式(2)中,得出在当前地应力时地层剪破裂时的理论临界剪应力
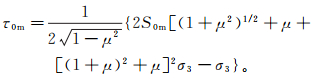 (7)
(7) 地层静态应力条件下的剪应力τ通常小于临界剪应力τ0m。当钻井过程中产生的剪应力大于τ0m时,地层将会出现剪切破裂,利用FMI测井能拾取到钻井诱导缝。
3 地层剪破裂影响因素分析张破裂的主要影响因素包含脆性指数、岩石力学参数和微裂缝等[15];剪破裂的主要影响因素包含地层的内摩擦系数、内聚强度和最大、最小水平地应力。由于地层矿物含量与内摩擦系数性质及脆性指数、地应力与岩石力学参数之间相互影响,所以需要分析地层岩石性质、矿物含量、地应力、脆性指数和岩石力学参数对剪破裂的影响。以下利用焦石坝区块龙马溪组4口井的测井数据,分析地层出现剪破裂的主要影响因素。
3.1 地层岩石性质地层的岩石性质包含地层的内聚强度和内摩擦角。根据公式(7)可以看出,地层的内聚强度和内摩擦角越大,则地层破裂所需要的剪应力就越大,即地层发生剪破裂就越难。
成像测井能直观有效地识别出钻井诱导裂缝的方位角,这个方位角是剪切裂缝与最大水平地应力方向的夹角,即图 2中的π-2θ。剪破裂面的方位可以由莫尔圆求出。根据图 2,得到地层岩石的内摩擦角与破裂面的方位角之间满足如下关系:
 (8)
(8)

|
| 图 2 库仑破裂准则示意图 Figure 2 Schematic diagram of Coulomb rupture criterion |
|
|
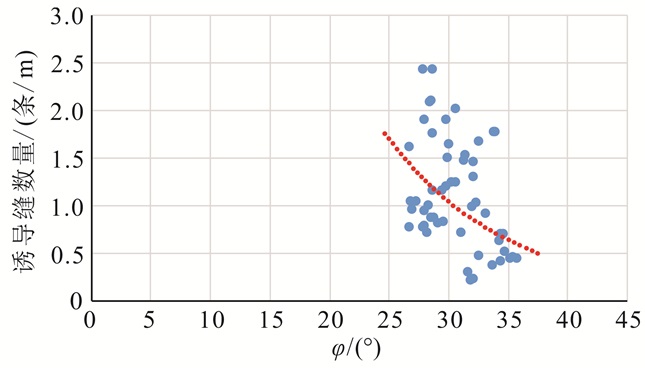
即利用成像测井拾取的裂缝方位角来计算地层的内摩擦角。理论分析发现,内摩擦角的大小与发生破裂的难易程度成反比。实际成像测井资料拾取的地层内摩擦角与每米井段中的诱导缝数量之间呈反比关系(图 3),即地层内摩擦角越小,地层诱导缝数量越大,越容易发生剪破裂;相反,地层内摩擦角越大,地层出现的诱导缝数量越少,越难发生剪破裂。
|
| 图 3 诱导缝数量与内摩擦角之间的关系 Figure 3 Diagram of the relationship between the number of induced fracture and the internal friction angle |
|
|
不同的矿物在不同的状态下具有不同的内摩擦系数。内摩擦系数一般由试验确定,根据前人的研究结果[16],发现石英质砂岩的内摩擦系数变化范围为0.35~0.50,铁质石英岩为0.35~0.45,石灰岩为0.25~0.35,花岗岩为0.30~0.40,泥灰岩为0.20~0.30,黏土为0.11~0.29。可以看出,黏土的内摩擦系数较低,石英的内摩擦系数较高,如果石英之间充满了黏土(蒙脱石、蛭石和伊利石),内摩擦系数将会急剧减小,使摩擦滑动变得十分容易。
地层中矿物的类型和含量对地层的综合内摩擦系数有很大的影响,不同的矿物组合使地层的内摩擦系数不同。内摩擦系数越大,则地层发生剪破裂的可能性就越小;相反地,内摩擦系数越小,则地层发生剪破裂的可能性就越大。利用FMI测井拾取的钻井诱导缝数量,分析诱导缝数量与地层黏土含量之间关系,发现地层中黏土含量越高,地层出现诱导缝数量越大(图 4)。图 4中地层为页岩地层,该页岩地层中,砂岩中间夹有一定量的泥岩,泥岩的存在使页岩地层的内摩擦系数减小,泥岩体积分数越高造成内摩擦系数越小,页岩地层发生剪破裂越容易。利用实际成像资料拾取钻井诱导缝数量,表明地层中存在一定量的泥岩时会产生剪切破裂,并随着泥质体积分数的增高,钻井诱导缝数量逐渐增多。但当泥质体积分数大于0.6时,基本上没有出现钻井诱导缝;可能的原因是泥质体积分数很高之后,地层逐渐变成塑性地层。因此地层中矿物含量对地层剪破裂有较大的影响,当泥质体积分数为0.25~0.65时,泥质体积分数越高,地层越容易发生剪破裂。
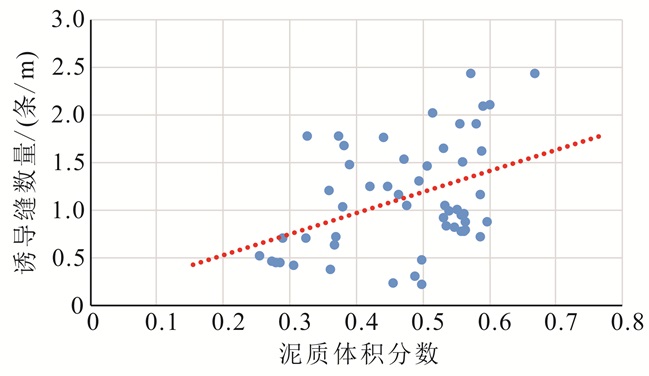
|
| 图 4 诱导缝数量与泥质体积分数之间的关系 Figure 4 Diagram of the relationship between the number of induced fracture and the shale content |
|
|
利用XMAC(偶极子声波)测井资料等能计算出地层的最大、最小水平地应力的大小及方向。根据地层地应力计算模型知道,地应力大小由上覆岩层的压力、孔隙压力和构造应力决定,同一深度上覆岩层压力和孔隙压力是各向同性的、数值相同的物理量,所以主要是构造应力不同导致地应力存在各向异性。地层在沉积、构造运动变化过程中具有一定的方向性,在地层构造运动方向存在最大作用力,而在其他的某一方向存在最小作用力,因此地层在现今应力场就出现了最大、最小构造应力系数和最大、最小构造应力。
根据公式(6)知道地层是否发生剪破裂还跟最大水平地应力有关:最大水平地应力越大,则地层发生剪破裂的难度越大;相反地,最大水平地应力越小,则地层发生剪破裂越容易。地层剪破裂的方向为最大水平地应力方向。将FMI测井资料拾取的某页岩地层中裂缝数量与XMAC成像测井资料评价的地层地应力大小进行比较(图 5):最大水平地应力与钻井诱导缝数量之间有一定的关系,表现为最大水平地应力越大,诱导缝数量较小。如图 6所示,最小水平地应力与钻井诱导缝数量相关性弱,主要原因是钻井过程中地层发生剪破裂的方向接近最大水平地应力方向,当地层剪应力大于临界剪应力时产生剪破裂,与地层的最小水平地应力基本无关。因此,最大水平地应力是决定地层是否发生剪破裂的重要影响因素之一。
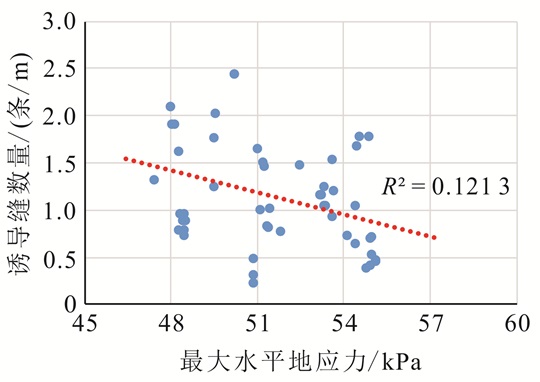
|
| R.相关系数。 图 5 诱导缝数量与最大水平地应力之间的关系 Figure 5 Diagram of the relationship between the number of induced fracture and horizontal maximum stress |
|
|

|
| 图 6 诱导缝数量与最小水平地应力之间的关系 Figure 6 Diagram of the relationship between the number of induced fracture and horizontal minimum stress |
|
|
地层脆性大小表示其变形能力大小,根据应变变形大小就可以定义地层的弹塑性质。岩石在一定条件下可视为弹性体,在长期的重力和应力作用下会发生变形,岩石的变形性质称为岩石的本构关系,分别是脆性、延性和脆性-延性过渡[16]。Evans等[17]把变形程度小于1%定义为脆性,大于5%定义为延性,其他为脆性-延性过渡。地层脆性指数通常用试验方法来确定,也可以用测井资料来评价。用测井资料评价地层脆性指数方面,有学者提出了用归一化的弹性模量和泊松比的方法[18];由于矿物存在脆性矿物和塑性矿物,也有人直接用矿物体积分数表达脆性指数模型[19-21]。如图 7所示,用脆性矿物体积分数来表示地层脆性指数,地层分为富含有机质和不含有机质地层,与FMI测井资料拾取的钻井诱导缝数量进行比较,发现不含有机质地层出现诱导缝数量随脆性指数增高而减小,但是富含有机质地层两者之间没有明显的关系。通常地,把硅质类和灰质类矿物看成脆性矿物,泥质类矿物看成延性矿物。因此,当脆性指数高时,泥质类矿物含量较低,导致地层的内摩擦系数较大,所以地层更难发生剪破裂,FMI测井拾取的钻井诱导缝数量越少;但是地层富含有机质时,地层剪破裂的随机性可能会更大。脆性指数也是影响地层剪破裂的因素之一,其本质仍然是不同的矿物具有不同的内摩擦系数,不同矿物组合时满足不同的剪破裂条件。

|
| 图 7 诱导缝数量与脆性指数之间的关系 Figure 7 Diagram of the relationship between the number of induced fracture and brittleness index |
|
|
杨氏模量、泊松比等力学参数用于计算地层的地应力,分析岩石力学参数对地层剪破裂的影响,有利于全面了解地层发生剪破裂的影响因素。通过声波测井资料获得地层岩石力学参数,与FMI测井拾取的钻井诱导缝数量进行比较,如图 8和图 9所示,图中为垂直井钻井过程中剪破裂产生的诱导缝数量,诱导缝延伸方向主要为垂直方向。从图 8和图 9可以看出,垂直方向的杨氏模量和泊松比与钻井诱导缝数量没有明显的变化关系。
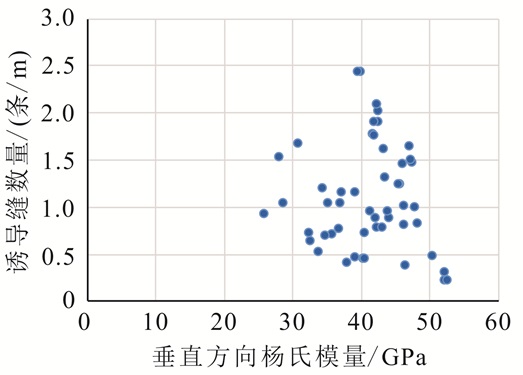
|
| 图 8 诱导缝数量与垂直方向杨氏模量之间的关系 Figure 8 Diagram of the relationship between the number of induced fracture and vertical Young's modulus |
|
|
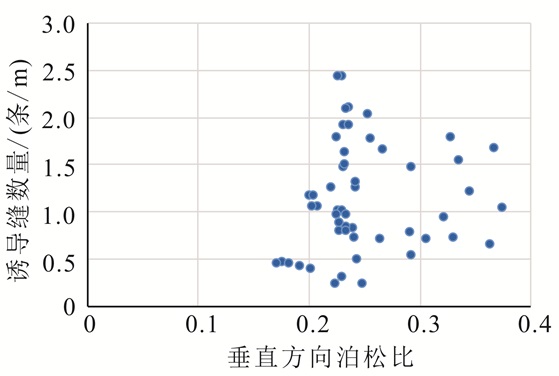
|
| 图 9 诱导缝数量与垂直方向泊松比之间的关系 Figure 9 Diagram of the relationship between the number of induced fracture and vertical Poisson's ratio |
|
|
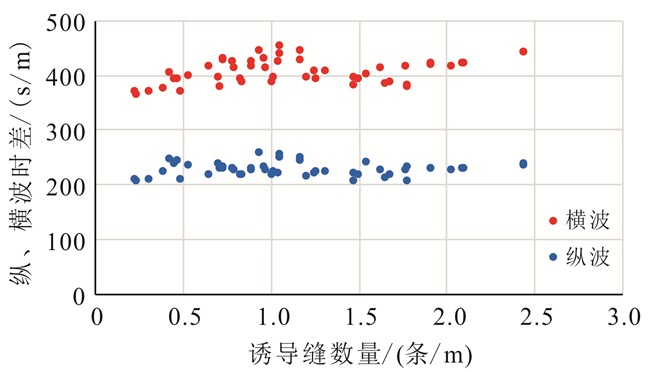
地层的纵、横波时差反映了地层中矿物、流体、孔隙结构和地应力等性质,所以地层的纵、横波时差在一定程度上间接地反映了地层是否出现剪破裂的特性。图 10为地层纵、横波时差与钻井诱导缝数量对比关系图,从图中看出,地层中出现的钻井诱导缝数量与地层的纵、横波时差没有明显的变化关系。
|
| 图 10 纵、横波时差与诱导缝数量之间的关系 Figure 10 Diagram of the relationship between longitudinal, transverse wave time difference and the number of induced fracture |
|
|
钻井过程中地层是否发生剪破裂,主要取决于剪应力大小是否满足库仑破裂条件。根据地层剪破裂模型公式(7)可知,地层发生剪破裂主要与内摩擦系数和地应力大小相关。FMI测井资料能得到地层的内摩擦系数,而且地层中内摩擦系数低的矿物含量越高,则地层的内摩擦系数越低。因此,假设不同矿物含量下的内摩擦系数模型为
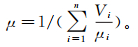 (9)
(9) 式中:Vi为第i种矿物的体积分数;μi为第i种矿物的内摩擦系数;n为矿物种类数目。
模型(9)中,内摩擦系数越小的矿物体积分数越高,则地层的内摩擦系数下降越快,与先验的认识是一致的。
4.2 模型的建立地层剪破裂难易程度主要由内摩擦系数决定,内摩擦系数越大越难发生破裂,内摩擦系数越小越易发生破裂。在复杂矿物地层中,黏土矿物的内摩擦系数是最小的,即泥质体积分数越大,则地层内摩擦系数越小。通过分析实测井内摩擦角与泥质矿物含量之间的关系,发现泥质体积分数与内摩擦角相关性很强(图 11),两者的相关系数达到0.81;说明利用泥质体积分数能有效表征内摩擦角和内摩擦系数。

|
| 图 11 内摩擦角与泥质体积分数之间的关系 Figure 11 Diagram of the relationship between the internal friction angle and the content of mud |
|
|
用测井资料中的自然伽马或伽马能谱能有效地计算出泥质体积分数,然后利用泥质体积分数计算出地层的内摩擦角和内摩擦系数:
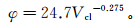 (10)
(10) 式中,Vcl为泥质体积分数。
将式(10)和地层实际的内聚强度代入式(7),得到地层出现剪破裂的模型:
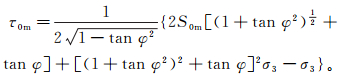 (11)
(11) 式中,S0m由钻井时出现诱导缝的地应力确定。
钻井过程中,当地层的实际剪应力大于模型(11)中的临界剪切应力时,地层将会出现钻井诱导缝。该模型避免了求地层的复杂矿物含量,而且每种矿物的内摩擦系数变化范围较大,用相关系数最高的泥质体积分数建立的内摩擦角估算模型有利于减少内摩擦系数的计算误差。
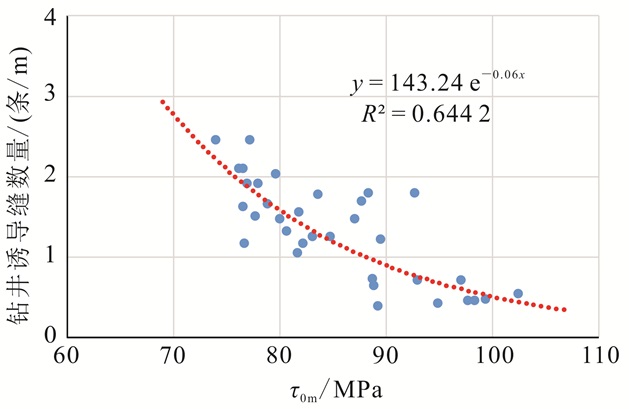
5 地层剪破裂模型的检验利用偶极子声波测井资料确定出最大、最小水平地应力[22];利用自然伽马测井资料计算出地层泥质体积分数,采用式(10)和式(11)计算地层剪破裂临界剪应力。利用FMI测井资料能识别钻井过程中出现的钻井诱导缝,通过比较钻井诱导缝数量与所计算剪破裂临界剪应力值之间的关系,验证模型的准确性。从图 12看出,τ0m与钻井诱导缝数量呈负相关关系,R2为0.644 2,说明两者的相关性较好。同时,τ0m越高,地层出现剪破裂越难,出现剪切诱导缝的数量越少;反之亦然。
|
| 图 12 利用测井资料计算钻井诱导缝数量与地层临界剪应力关系图 Figure 12 Calculation of the number of induced fractures and critical shear fracture stress of formation using logging data |
|
|
1) FMI测井资料能有效地确定钻井诱导缝方位和裂缝发育的线密度,钻井诱导缝反映了地层的剪破裂性质。
2) 通过对地层剪破裂的影响因素分析,发现地层的内摩擦角是最重要的影响因素,可用地层的泥质体积分数来表征其内摩擦角。
3) 利用内摩擦角与泥质体积分数的回归公式和地应力大小,建立起地层发生剪破裂的临界剪应力模型,模型计算的临界剪应力结果与钻井诱导缝数量之间呈反比关系。
| [1] |
赵金洲, 任岚, 胡永全, 等. 裂缝性地层射孔井破裂压力计算模型[J].
石油学报, 2012, 33(5): 841-845.
Zhao Jinzhou, Ren Lan, Hu Yongquan, et al. A Calculation Model of Breakdown Pressure for Perforated Wells in Fractured Formations[J]. Acta Petrolei Sinica, 2012, 33(5): 841-845. DOI:10.7623/syxb201205014 |
| [2] |
金衍, 陈勉, 张旭东. 天然裂缝地层斜井水力裂缝起裂压力模型研究[J].
石油学报, 2006, 27(5): 124-126.
Jin Yan, Chen Mian, Zhang Xudong. Hydraulic Fracturing Pressure Models for Vertical Wells in Naturally Fractured Formation[J]. Acta Petrolei Sinica, 2006, 27(5): 124-126. DOI:10.7623/syxb200605026 |
| [3] |
金衍, 张旭东, 陈勉. 天然裂缝地层中垂直井水力裂缝起裂压力模型研究[J].
石油学报, 2005, 26(7): 113-118.
Jin Yan, Zhang Xudong, Chen Mian. Initiation Pressure Models for Hydraulic Fracturing of Directional Wells in Naturally Fractured Formation[J]. Acta Petrolei Sinica, 2005, 26(7): 113-118. |
| [4] |
谢海峰, 饶秋华, 谢强, 等. 脆性岩石高温剪切(Ⅱ型)断裂的微观机理[J].
中国有色金属学报, 2008, 18(8): 16-20.
Xie Haifeng, Rao Qiuhua, Xie Qiang, et al. Plane Shear (Model Ⅱ) Fracture Experiment Analysis of Brittle Rock at High Temperature[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(8): 16-20. |
| [5] |
李守定, 李晓, 郭静芸, 等. 岩石拉伸剪破裂试验研究[J].
工程地质学报, 2014, 22(4): 655-666.
Li Shouding, Li Xiao, Guo Jingyun, et al. Research of Rock Failure Testing Under Combined Shear and Tension[J]. Journal of Engineering Geology, 2014, 22(4): 655-666. |
| [6] |
吴子科. 脆性岩石裂纹尖端扩展状态的混沌动力学分析[D]. 青岛: 山东科技大学, 2007.
Wu Zhike. Chaotic Analysis on Extended State of Crack in Brittle Rock[D]. Qingdao: Shandong University of Science and Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10424-2008013831.htm |
| [7] |
牛虎林, 胡欣, 徐志强, 等. 基岩油气藏裂缝性储层的成像测井评价及裂缝预测[J].
石油学报, 2010, 31(2): 264-269.
Niu Hulin, Hu Xin, Xu Zhiqiang, et al. Evaluation of Imaging Logging and Fracture Prediction in Fractured Basement Reservoirs[J]. Acta Petrolei Sinica, 2010, 31(2): 264-269. DOI:10.7623/syxb201002014 |
| [8] |
周祥. 不同泥质含量砂岩三轴渗透试验研究[J].
水文地质工程地质, 2017, 44(1): 84-90.
Zhou Xiang. An Experimental Study on Permeability of Sandstone with Different Shale Contents Under 3-D Stress Conditions[J]. Hydrogeology & Engineering Geology, 2017, 44(1): 84-90. |
| [9] |
丁文龙, 漆立新, 吕海涛, 等. 利用FMI资料分析塔河油田南部中-下奥陶统储层构造应力场[J].
现代地质, 2009, 23(5): 852-859.
Ding Wenlong, Qi Lixin, Lü Haitao, et al. Analysis of the Lower-Middle Ordovician Reservoir Tectonic Stress Field Using FMI Data in the South of Tahe Oilfield[J]. Geoscience, 2009, 23(5): 852-859. |
| [10] |
秦军. 利用成像测井技术识别钻井诱导缝[J].
内蒙古石油化工, 2006, 32(10): 116-117.
Qin Jun. Using Imaging Logging to Recognize Drilling Induced Fractures[J]. Inner Mongolia Petrochemical Industry, 2006, 32(10): 116-117. DOI:10.3969/j.issn.1006-7981.2006.10.054 |
| [11] |
谢冰, 文龙, 李梅. 川东北部飞仙关组裂缝发育状况分析[J].
天然气勘探与开发, 2007, 30(1): 38-44.
Xie Bing, Wen Long, Li Mei. Analysis of Fracture Development in Feixianguan Formation, North of East Sichuan[J]. Natural Gas Exploration and Development, 2007, 30(1): 38-44. |
| [12] |
宋鹏. 王府断陷火石岭组火山岩储层裂缝特征与分布规律[J].
世界地质, 2015, 23(3): 716-725.
Song Peng. Fracture Characteristics and Distribution of Volcanic Reservoir of Huoshiling Formation in Wangfu Fault Depression[J]. Global Geology, 2015, 23(3): 716-725. |
| [13] |
王振宇, 刘超, 张云峰, 等. 库车坳陷K区块冲断带深层白垩系致密砂岩裂缝发育规律、控制因素与属性建模研究[J].
岩石学报, 2016, 32(3): 865-876.
Wang Zhenyu, Liu Chao, Zhang Yunfeng, et al. A Study of Fracture Development, Controlling Factor and Property Modeling of Deep-Lying Tight Sandstone in Cretaceous Thrust Belt K Region of Kuqa Depression[J]. Acta Petrologica Sinica, 2016, 32(3): 865-876. |
| [14] |
王玉华. 电成像测井在大庆火成岩储层解释中的应用[J].
大庆石油地质与开发, 2008, 27(6): 128-130.
Wang Yuhua. Application of Electrical Imaging Logging in the Well Logging Interpretation of Igneous Rock Reservoir in Daqing[J]. Petroleum Geology & Oilfield Development in Daqing, 2008, 27(6): 128-130. |
| [15] |
廖东良, 肖立志, 张元春. 基于矿物组分与断裂韧度的页岩地层脆性指数评价模型[J].
石油钻探技术, 2014, 42(4): 37-41.
Liao Dongliang, Xiao Lizhi, Zhang Yuanchun. Evaluation Model for Shale Brittleness Index Based on Mineral Content and Fracture Toughness[J]. Petroleum Drilling Techniques, 2014, 42(4): 37-41. |
| [16] |
陈颙, 黄庭芳, 刘恩儒.
岩石物理学[M]. 合肥: 中国科技大学出版社, 2009.
Chen Yong, Huang Tingfang, Liu Enru. Petrophysics[M]. Hefei: University of Science and Technology of China Press, 2009. |
| [17] | Evans B, Fredrich J, Wong T F. The Brittle-Ductile Transition in Rocks:Recent Experiment and Theoretical Progress[J]. America Goephys Union, 1990, 56: 1-20. |
| [18] | Rickman R, Mullen M, Petre E, et al. A Practical Use of Shale Petrophysics for Stimulation Design Optimization: All Shale Plays are not Clones of the Barnett Shale[C]//SPE Annual Technical Conference and Exhibition. Denver: SPE, 2008: 21-24. |
| [19] | Jarvie D M, Hill R J, Ruble H J, et al. Uncon-ventional Shale-Gas Systems:The Mississippian Barnett Shale of North-Central Texas as One Model for Thermogenic Shale-Gas Assessment[J]. AAPG Bulletin, 2007, 91(4): 475-499. DOI:10.1306/12190606068 |
| [20] | Dan B, Simon H, Jennifer M, et al. Preophysical Evaluation for Enhancing Hydraulic Stimulation in Horizontal Shale Gas Wells[C]//SPE Annual Technical Conference and Exhibition. Florence: SPE, 2010: 19-22. |
| [21] |
王冠民, 熊周海, 张婕. 岩性差异对泥页岩可压裂性的影响分析[J].
吉林大学学报(地球科学版), 2016, 46(4): 1080-1089.
Wang Guanmin, Xiong Zhouhai, Zhang Jie. The Impact of Lithology Differences to Shale Fracturing[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(4): 1080-1089. |
| [22] |
王晓杰, 彭仕宓, 吕本勋, 等. 用正交偶极阵列声波测井研究地层地应力场[J].
中国石油大学学报(自然科学版), 2008, 32(4): 42-46.
Wang Xiaojie, Peng Shimi, Lü Benxun, et al. Researching Earth Stress Field Using Cross-Dipole Acoustic Logging Technology[J]. Journal of China University of Petroleum, 2008, 32(4): 42-46. |


