0 引言
地震数据在采集过程中总是表现出空间不连续性:一方面是由于实际勘探环境非常复杂,如村庄、河流等障碍物的存在造成观测系统的改变;另一方面是由于经济因素的制约,造成检波器和炮点不可能连续布置,使地震数据缺失。但是完整的地震数据是许多重要处理方法的前提,如表层相关多次波消除、波动方程偏移和时移地震等。常规的地震数据插值方法往往对地震数据的平稳性要求较高,如地震同相轴为平稳平面波假设,但地震数据本质上是非平稳的,开发能够有效解决非平稳复杂波场的缺失数据重建问题具有重要意义。
预测滤波器在地震数据处理和分析中具有重要的作用,例如在地震数据反褶积[1]和压制随机噪声[2-3]等方面。预测滤波器可以有效地表征地震数据能量谱[4-5],为解决地球物理反演问题提供了一种有效的近似估计方法,也为恢复缺失的地震信息指明了方向。地球物理学者对预测滤波器的研究取得了一定的进展。预测滤波器的本质是信号自回归,在时间-空间域和频率-空间域都具有适用性,而时间-空间域的滤波能够避免出现假频现象[6]。可以利用预测误差滤波器(由预测滤波系数构成)的尺度缩放不变性计算反空间假频地震倾角模式,对缺失的地震数据进行反假频插值[7]。
随着勘探区域地下介质复杂性的增加,地震信号的非平稳性往往也愈加明显,如何将传统的平稳预测滤波处理方法应用到非平稳数据是一个重要的研究方向。常规的解决方式将数据进行重叠时窗处理,或者假设数据是局部平稳[8-9]。Fomel[10]提出了基于整形正则化算子的非平稳自回归方法,并用于解决地球物理反演问题,其扩展可应用于时频分析和非平稳多项式拟合。Liu等[11]提出应用非因果正则化非平稳自回归(NRNA)进行频率-空间域的随机噪声压制,在二维地震数据中取得了理想的效果,继而将滤波系数在空间方向进行扩展,开发了三维非平稳自回归对地震数据的随机噪声压制方法。Liu等[12]利用整形正则化条件约束预测误差滤波系数,对带有空间假频的地震数据进行了有效的重建。但是这些方法在解决滤波器系数的时空变化属性表征问题时都增加了额外的计算成本。流预测滤波器[13]可以使滤波系数随着数据的变化同时更新,运算形式仅仅表现为信号的褶积,并且不需多次迭代,在提高运算效率的同时降低了内存成本。流预测滤波器对非平稳数据具有预测逆运算的特点,可以快速地完成缺失数据重建。但是,缺失的地震道对滤波器系数的准确估计有较大影响,很难保证准确的插值效果。
近年来,很多地球物理学家从不同的角度对多次波的问题进行探讨和尝试,并不局限于视其为噪声从地震数据中去除,而是如何更好地利用多次波中所包含的地下反射信息。多次波在偏移成像[14]和联合反演[15]中都得到了一定的应用。构建准一次波的插值方法[16-17]以及直接利用含有多次波的地震数据构建拟地震数据的插值方法[18],主要是利用地震数据的动力学可预测特性,将多次波中蕴含的有效信息提取出来。利用多次波的信息形成虚拟一次波,能够为基于流预测滤波的插值方法提供滤波器系数估计的数据来源。
本文针对流预测滤波器具有较准确非平稳波场能量谱估计和较高运算效率的特征,通过虚拟一次波为缺失数据提供合理的滤波估计,利用自回归预测理论对缺失数据进行重建,以解决复杂叠前地震波场的数据缺失问题。
1 理论基础 1.1 预测滤波插值方法预测滤波器基于自回归理论,利用预测滤波器进行地震数据的重建可以表述为两步求解反问题的过程。第一步,利用最小二乘方法求解反问题,估计滤波系数。例如,给定一组数据d(其中可能包含缺失数据),利用预测滤波器估计滤波系数,当dn+1已知时,基于预测误差近似为零的自回归表达公式为
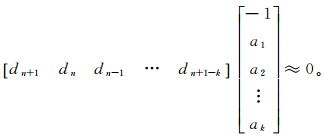 (1)
(1) 式中:ak为预测滤波系数;n、k为自然数。其矩阵表达形式为
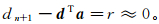 (2)
(2) 式中:r为残差;d为数据的矩阵形式;a为预测滤波系数的矩阵形式。
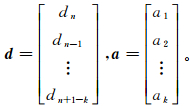
利用最小二乘反演估计滤波系数,表达式为
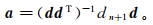 (3)
(3) 第二步,利用求得的滤波系数对缺失的地震数据进行恢复。当dn+1为缺失数据时,通过自回归方程再次求解公式(2),并利用第一步估计出的预测滤波系数可以完成对缺失数据的重建,其计算表达式为
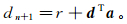 (4)
(4) 由于传统的预测滤波方法很难表征复杂的非平稳地震数据,直接利用传统的预测滤波器进行数据插值会引起较大的误差;而自适应预测滤波器[13]的结构造成计算资源占用率过高,很难满足实际生产的需求。因此,利用改进的流预测滤波方法进行滤波器系数的非迭代计算。
1.2 流预测滤波器估计流预测滤波器(streaming PF)基于非平稳数据的局部平稳假设,滤波器系数为局部相似。假设滤波器系数随着每一个新增数据dn+1而更新,并且新的滤波系数a与前一组滤波系数a近似,将此作为滤波系数计算的约束条件。可以将其与公式(2)组合成一个线性方程组,表达式为
 (5)
(5) 式中:I为单位矩阵;λ为近似参数,表示滤波系数a与相邻滤波系数a的线性相似度。
在求解方程组的过程中,采用Sherman-Morrison公式[19]进行解析表达式推导,滤波系数估计的表达式为
 (6)
(6) 新的滤波器系数通过加上一个按一定尺度缩放的数据而不断更新,实现自适应变化。这个尺度与前一个滤波器系数和残差存在比例关系(残差由前一个滤波器系数和数据点积(dTa)求得),公式(6)得到的更新滤波器系数只进行代数运算(向量的点积)而没有迭代的需求,此时预测滤波器的非平稳数据表征问题得到解决。但是在数据重建过程中,公式(2)中d所包含的缺失数据会造成预测滤波器系数的较大偏差,进而导致插值精度的降低,直接利用缺失数据的滤波系数估计可以转换为利用近似数据的滤波估计,只要近似数据具有与原始数据相似的预测特征即可。
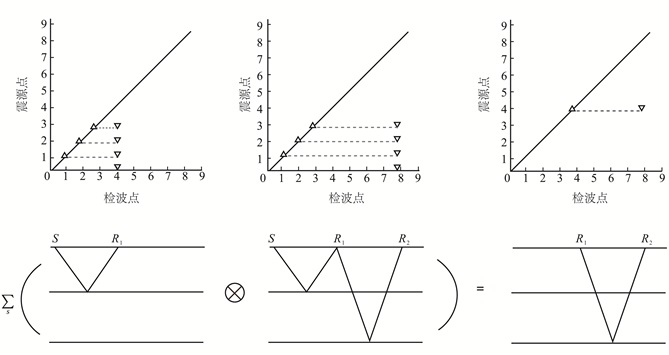
1.3 基于虚拟一次波的预测滤波估计多次波可以通过地震数据本身的褶积预测出来,将一次波“升阶”为多次波。反之,可以利用互相关代替褶积,将多次波“降阶”,利用地震数据本身的多次波提取出有效的一次波信息,称为虚拟一次波。构建虚拟一次波的具体实现算法是,对同一个炮集的原始记录和多次波记录进行互相关,一次波的接收点则成为虚拟一次波的震源点,对同一震源进行叠加,可以提高虚拟一次波的信噪比,继而得到完整的道集记录。图 1给出了构建“虚拟一次波”的示意图。虚拟一次波具有与原始一次波相似的动力学特征,由于其利用观测系统的坐标关系进行叠加计算,因此不受缺失数据的影响,可以代替缺失数据进行预测滤波器的系数估算。
|
| 图 1 虚拟一次波射线轨迹示意图 Figure 1 Raypaths of the pseudoprimaries |
|
|
在二维观测系统中(图 1),利用SR1的一次波数据与SR2的多次波数据进行互相关运算,可以得到R1R2的虚拟一次数据,其与原始数据中以R1为震源点在R2接收的一次波有着相似的动力学特征,表达式为
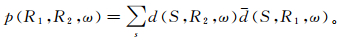 (7)
(7) 式中:p(R1, R2, ω)表示构建的虚拟一次波频率域数据;ω为频率;d(S, R2, ω)表示以S为震源、在R2接收的频率域多次波数据;d(S, R1, ω)表示以S为震源、在R1接收的频率域一次波数据的共轭形式。
虚拟一次波虽然不能完全与原始数据相匹配,在振幅、相位、子波等方面存在误差,但不影响预测滤波器的估计。将虚拟一次波作为初始数据,利用公式(6)估计滤波系数,并将其代入公式(4)求解插值表达式
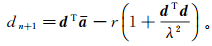 (8)
(8) 假设预测滤波残差r为零,则数据重建结果表达式为
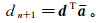 (9)
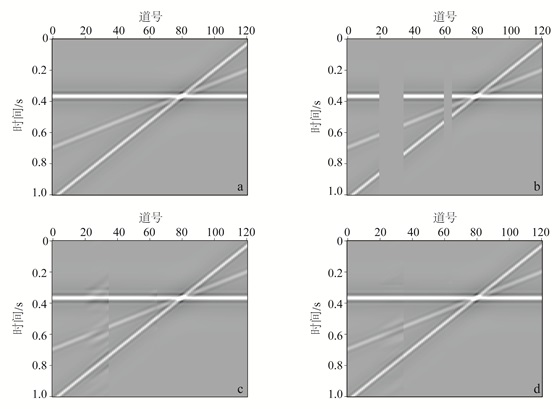
(9) 首先选取Abma等[20]提出的平面波模型数据进行测试,如图 2所示。该模型提供了两个数据体,分别为标准数据和偏差数据(即振幅、相位与标准数据不匹配)。这里利用该模型验证本文方法的有效性。图 2a为标准数据,时间长度为1 s,共计120道。图 2b为缺失数据,在第20道的位置出现较严重的缺失(15道),在第60道位置出现较小的缺失(5道)。图 2c为直接使用图 2b进行流预测滤波器系数估计、再对缺失位置进行数据重建的结果,可见在缺失较严重的位置并不能得到理想的重建结果。图 2d为利用偏差数据进行滤波系数估计、再对缺失数据进行重建的结果,图中同相轴的连续性和能量得到了比较准确的恢复。
|
| a.标准数据;b.缺失数据;c.使用缺失数据滤波系数的重建结果;d.使用偏差数据滤波系数的重建结果。 图 2 Abma模型测试 Figure 2 Abma model test |
|
|
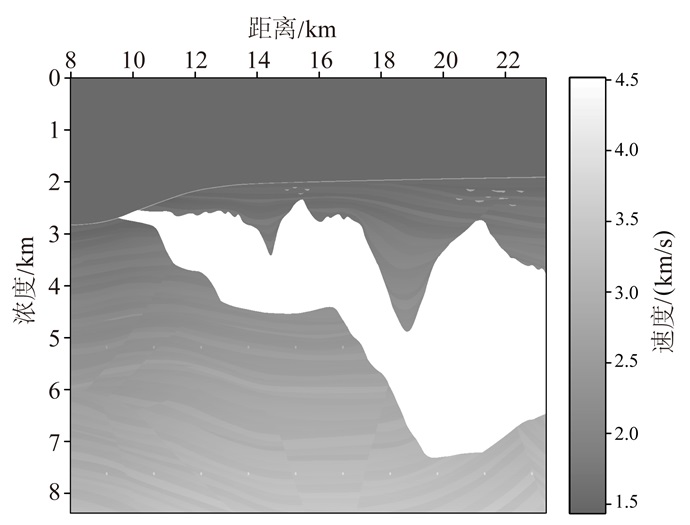
为了验证本文方法对复杂地震数据的有效性,接下来测试Sigsbee 2B模型,利用有限差分正演叠前地震数据。模型中包含一个不规则的盐丘体反射层,使得正演数据体现出复杂的地震波场特征。图 3为Sigsbee 2B的速度模型,正演数据时间采样间隔为8 ms,共计1 000个采样点;由于空气、水和盐丘体存在较大的波阻抗差,所以多次波发育明显,为虚拟一次波的构建提供了数据保证。图 4a为去除20%地震道的正演记录,图 4b为利用图 4a构建的虚拟一次波数据,其与原始数据(图 4a)具有相似的动力学特征。
|
| 图 3 Sigsbee 2B速度模型 Figure 3 Velocity of Sigsbee2B model |
|
|
|
| 图 4 原始缺失数据(a)和虚拟一次波数据(b) Figure 4 The missing data (a) and the pseudoprimaries data of Sigsbee2B model(b) |
|
|
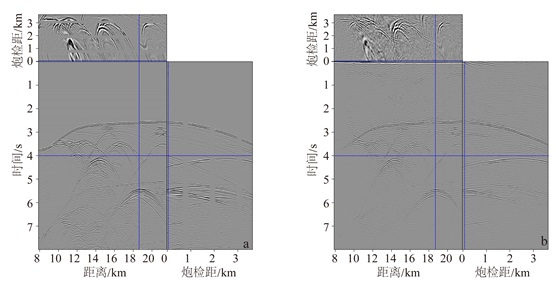
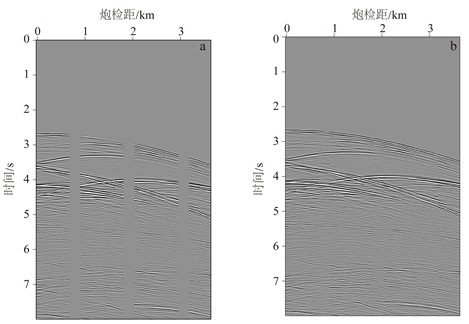
选取测线坐标为14 km的完整单炮数据(图 5a)测试插值效果,缺失数据中有3个较大的数据缺口。利用流预测滤波器对虚拟一次波数据进行滤波估计,该方法只需要两个向量的褶积而不需迭代,大大降低了运算成本,根据公式(9)可以高效地完成缺失数据的重建。滤波器的尺寸为20(时间)×5(空间),近似系数为1.22。图 5b为插值结果,结果表明本文的方法在处理复杂地震数据时,可以快速和准确地对缺失地震道完成重建工作。
|
| a.缺失数据单炮记录;b.本文方法数据重建结果。 图 5 Sigsbee2B模型数据重建结果 Figure 5 Result of the reconstruction of Sigsbee2B model |
|
|
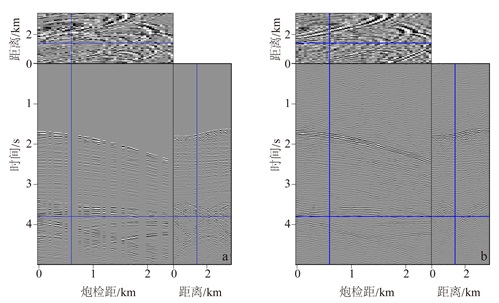
选取墨西哥湾某地区的三维地震数据进一步测试本文方法的稳定性。图 6a为随机缺失40%的炮集数据体,上部为3.8 s的时间切片,左下部为距离位置在1.7 km的单炮记录,右下部为0.5 km的共炮检距剖面。炮间距为0.05 km,共计80炮。实际地震资料中多次波和散射波都有明显的体现,在数据缺失较严重的位置很难判断同相轴的走向。
|
| 图 6 随机缺失40%的地震数据(a)和构建的虚拟一次波(b) Figure 6 Data with 40%randomly missing traces (a) and the pseudoprimaries data (b) |
|
|
在实际资料的处理中,利用Radon变换[21]或者在逆数据域下[22]有效地分离一次波和多次波,再通过多次波与一次波的互相关(公式(7))构建虚拟一次波(图 6b)。结果虽然出现了一定的随机噪声,但主要的同相轴信息得到了恢复,可以为本文的插值方法提供合理的滤波估计。
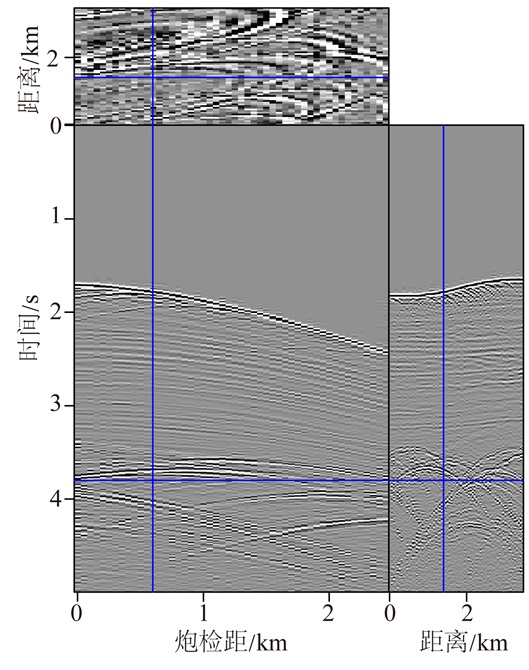
利用本文方法对三维地震缺失道进行数据重建。应用流预测滤波器对构建的虚拟一次波进行滤波估计,滤波器尺寸参数为25(时间)×5(空间)×10(空间),通过计算公式(9)对缺失数据进行重建,结果如图 7所示。浅层的海底反射以及非平稳的同相轴信息都得到了合理恢复,随机噪声并没有对重建结果产生明显的影响,在图中难以区分插值数据与原始数据的位置,说明插值结果具有较好的合理性。
|
| 图 7 本文方法数据重建结果 Figure 7 Result of the data reconstruction |
|
|
1) 本文提出基于流预测滤波器结合虚拟一次波的技术方案对缺失地震数据进行重建。在应用流预测滤波器估计滤波系数的过程中,将相邻滤波器系数具有比例相似性作为约束条件可快速有效地完成滤波估计,并利用数据本身多次波所蕴含的动力学信息预测缺失的地震数据,在数据插值过程中更合理地为滤波估计提供数据分析基础。
2) 理论模型测试结果表明,在缺失较严重的数据中,改进的流预测滤波插值方法可以获得更加理想的数据重建效果;实际地震数据处理结果表明,该方法可以有效地针对复杂非平稳地震波场的缺失问题进行求解。
| [1] | Robinson E A, Osman O M. Deconvolution 2[M]. Tulsa: Society of Exploration Geophysicists, 1996. |
| [2] | Canales L. Random Noise Reduction[J]. SEG Tech-nical Program Expanded Abstracts, 1984, 3(1): 525-527. |
| [3] | Liu G, Chen X, Du J, et al. Random Noise Attenu-ation Using f-x Regularized Nonstationary Autoregression[J]. Geophysics, 2012, 77(2): 61-68. DOI:10.1190/geo2011-0117.1 |
| [4] | Spitz S. Seismic Trace Interpolation in the F-X Domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [5] | Crawley S. Seismic Trace Interpolation with Nonsta-tionary Prediction-Error Filters[D]. Palo Alto: Stanford University, 2001. |
| [6] | Abma R. Least-Squares Separation of Signal and Noise with Multidimensional Filters[D]. Palo Alto: Stanford University, 1995. |
| [7] |
刘财, 李鹏, 刘洋, 等. 基于seislet变换的反假频迭代数据插值方法[J].
地球物理学报, 2013, 56(5): 1619-1627.
Liu Cai, Li Peng, Liu Yang, et al. Iterative Data Interpolation Beyond Aliasing Using Seislet Transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1619-1627. DOI:10.6038/cjg20130519 |
| [8] | Crawley S, Claerbout J. Interpolation With Smoothly Nonstationary Prediction-Error Filters[J]. SEG Technical Program Expanded Abstracts, 1999, 18: 181-196. |
| [9] | Curry W. Interpolation of Irregularly-Sampled Data with Nonstationary Multi-Scale Prediction-Error Filters[J]. SEG Technical Program Expanded Abstracts, 2003, 22(1): 1913-1917. |
| [10] | Fomel S. Shaping Regularization in Geophysical-Estimation Problems[J]. Geophysics, 2007, 24(1): R29-R36. |
| [11] | Liu G, Chen X. Noncausal f-x-y Regularized Nonsnu-tationary Prediction Filtering for Random Noise Attenuation on 3D Seismic Data[J]. Journal of Applied Geophysics, 2013, 93(2): 60-66. |
| [12] | Liu Y, Fomel S. Seismic Data Interpolation Beyond Aliasing Using Regularized Nonstationary Autoregression[J]. Geophysics, 2011, 76(5): V69-V77. DOI:10.1190/geo2010-0231.1 |
| [13] | Fomel S, Claerbout J. Streaming Prediction-Error Filters[C]//SEG Technical Program Expanded. [S. l. ]: SEG, 2016: 4787-4791. |
| [14] | Muijs R, Robertsson A J O, Holliger K. Prestack Depth Migration of Primary and Surface-Related Multiple Reflections:Part Ⅰ:Imaging[J]. Geophysics, 2007, 72(2): 3953-3957. |
| [15] | Brown M. Least-Squares Joint Imaging of Multiples and Primaries[J]. Geophysics, 2004, 70(5): 89-107. |
| [16] | Shan G, Guitton A. Migration of Surface-Related Multiples: Tests on Sigsbee 2B Datasets[C]//SEG Technical Program Expanded Abstracts. [S. l. ]: SEG, 2004: 153-162. |
| [17] | Curry W, Shan G. Interpolation of Near Offsets Using Multiples and Prediction-Error Filters[J]. Geophysics, 2010, 75(6): 225-226. |
| [18] | Guo S J, Li Z C, Tong Z Q, et al. Interpolation of Near Offset Using Surface-Related Multiples[J]. Applied Geophysics, 2011, 8(3): 225-232. DOI:10.1007/s11770-011-0284-2 |
| [19] | Hager W W. Updating the Inverse of a Matrix[J]. Siam Review, 1989, 31(2): 221-239. DOI:10.1137/1031049 |
| [20] | Abma R, Kabir N, Matson K H, et al. Comparisons of Adaptive Subtraction Methods for Multiple Attenuation[J]. SEG Technical Program Expanded Abstracts, 2002, 21(1): 277-280. |
| [21] | Foster D J, Mosher C C. Suppression of Multiple Reflections Using the Radon Transform[J]. Geophysics, 1992, 57(3): 386-395. DOI:10.1190/1.1443253 |
| [22] |
石颖, 刘洪, 历玉英. 逆数据域表面多次波压制方法[J].
吉林大学学报(地球科学版), 2011, 41(1): 271-276.
Shi Ying, Liu Hong, Li Yuying. Surface-Related Multiple Attenuation Method Investigation in Inverse Data Domin[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(1): 271-276. |



