2. 中海油研究总院有限责任公司, 北京 100027;
3. 海洋地质国家重点实验室(同济大学), 上海 200092
2. CNOOC Research Institute Co. Ltd, Beijing 100027, China;
3. State Key Laboratory of Marine Geology(Tongji University), Shanghai 200092, China
0 引言
波阻抗反演是储层预测的基础,其精度依赖于背景或低频速度模型的精度。因此,如何求取低频速度模型这一问题一直受到众多地球物理学家的关注[1-6]。到目前为止,已经提出了井控插值法、协克里金法、序贯高斯模拟法、速度谱转化法、多次迭代滤波法等多种方法[6-16]。其中:井控插值法需要钻井数量较多,且模型可靠程度受井间距离影响严重[3];基于地质统计学建模的方法(协克里金法和序贯高斯模拟法)虽然精度较高,但需要有较多样本点时统计结果才更可靠,并不适用于勘探早期阶段研究[4];常规地震资料处理过程中速度谱的精度较低,无法反映复杂储层的横向变化特征。
我国南海深水区普遍面临着勘探程度低、钻井数量有限、地层埋深跨度大、储层横向非均质性变化剧烈、断裂特征复杂的难题,在此地区上述模型构建方法的缺点体现得尤为突出,使储层及油气预测的成功率较低。因此,本文针对我国南海深水区勘探现状及已有低频模型构建方法的缺点,提出了一种基于立体层析反演技术的低频模型构建方法。该方法利用立体层析反演技术可以获得高精度速度模型的优势,结合有限的钻井信息对该速度模型进行标定,然后构建出符合深水区地震反演需求的低频模型,以期解决我国深水区少井、无井条件下地震储层反演过程中低频模型构建难的问题,提升深水储层预测的成功率。
1 立体层析反演理论“立体层析”的原词是stereo-tomography,最原始的“立体”表达的含义是Billiette等[17]所说的:由于将射线参数和射线出射坐标都引入了数据空间,相比仅仅使用旅行时的传统层析方法,其数据空间更为丰富和全面,故将这种方法命名为“立体层析”。立体层析是一种基于射线扰动理论的层析成像方法,除了旅行时之外,它将共炮道集和共检波点道集内局部同相轴的斜率(即慢度矢量水平分量)、炮点坐标、检波点坐标也纳入到数据空间。与此相对应,反演的模型分量也不仅限于速度,还包括反射点位置、反射层的局部倾角以及射线对的张角。其优势在于,数据的提取只依赖于局部相干同相轴的运动学信息,计算更为方便,可以同时反演速度、反射点位置与反射层局部形态[18-20]。它有两种实现方式:数据域立体层析和成像域立体层析。本文综合了数据域立体层析与成像域立体层析的优势,获得大大超出常规地震叠加速度谱精度的宏观速度模型。
1.1 数据域立体层析反演立体层析成像属于数据拟合类反演方法,即找到一个模型矢量,使正演得到的数据与拾取数据的误差达到最小。以常用的二范数衡量拟合误差作为目标泛函,则立体层析反演归结为如下泛函的求极值问题:
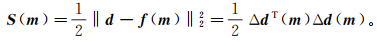 (1)
(1) 式中:m为模型空间;d为数据空间;f为反演过程中使用的正演算子;Δd(m)=d-f(m)。对上述二范数泛函S(m)求梯度即可获得最小平方意义下的线性方程组:
 (2)
(2) 式中,F为Frechet导数矩阵,可以通过射线扰动理论[21-22]求得。考虑到实际应用中噪音的存在,以及射线的覆盖密度不一定均匀,矩阵F一般是病态的,施加规则化后的泛函可写为如下新的误差泛函:
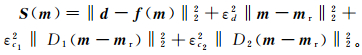 (3)
(3) 式中:εd2、εc12、εc22为选定的权因子;mr为参考模型;D1和D2分别是对模型空间更新量在横向和纵向上的一阶差分算子;εd2‖m-mr‖22为阻尼项,控制每次迭代的模型更新量较小,保证收敛过程总体的稳健;εc12‖D1(m-mr)‖22和εc22‖D2(m-mr)‖22分别为约束速度模型在横向和纵向上的光滑程度。这种正则化不仅可以保证反演结果比较光滑,也可以保证反演结果与参考模型比较接近。
施加正则化之后需要求解的线性方程组为
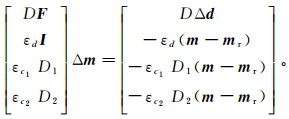 (4)
(4) 式中,I为单位矩阵。利用最小二乘方法(LSQR)可以在最小二乘意义下高效地求解大规模稀疏矩阵方程组(4),完成数据域立体层析成像。这些正则化因子依据不同的实际数据,需要通过测试得到。在本文的实际数据中,这些权因子分别为εd=0.001;εc1=0.02;εc2=0.02。
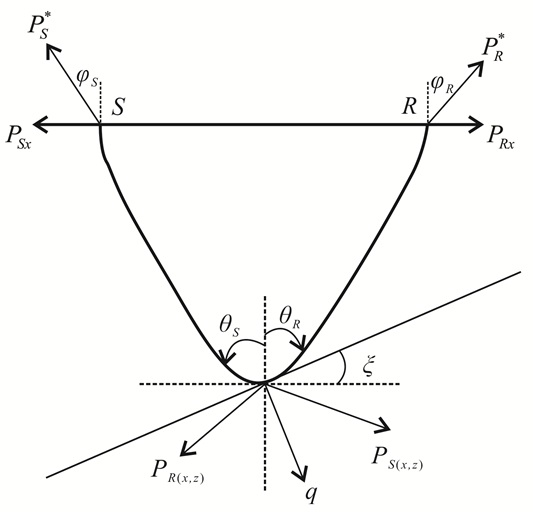
1.2 成像域立体层析反演成像域立体层析的要点是先用初始速度模型进行成像,然后从初始成像体的运动学信息出发,通过实施运动学反偏移+P参数(P为慢度)校正获得正确的立体层析数据空间信息(图 1)。在克希霍夫偏移过程中,成像条件应满足
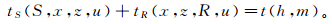 (5)
(5)
|
| 图 1 运动学反偏移+P参数校正图示 Figure 1 Illustration of kinematic demigration +P parameter correction |
|
|
式中:tS和tR分别为成像点(x, z)到炮点S、检波点R的单程走时;t为总旅行时,t=tS+tR;u为地下的速度;h为半偏移距;m为炮检距的中心点位置。
P参数校正公式为:
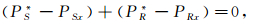 (6a)
(6a) 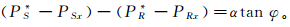 (6b)
(6b) 式中:PS*、PR*分别为射线出射到地表炮点和检波点时的慢度水平分量;PSx、PRx分别为以初始速度从地下反射点传播至地表炮点和检波点时的视慢度水平分量[22];α=cos ξcos θ,ξ为地层倾角,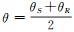
运动学反偏移实质上就是射线从地表出发,找到正确的地表炮检点位置的过程。
运动学反偏移是在叠前偏移之后的道集上实施的。首先,在共偏移距成像剖面内拾取反射点位置(x, h, z),并搜索其对应的构造倾角ξ。然后,在共偏移距成像点道集内搜索对应剩余曲率的斜率信息tan φ。在获得上述信息后,即可以利用初始偏移速度模型进行射线追踪。为了找到地表的正确炮检点位置,需要不断调整散射角,使两根射线出射到地表的位置之间的距离恰好等于2h。这时记录下出射到地表的视慢度信息PSx、PRx,以及总旅行时t。由于初始偏移速度不可能是准确的,必须通过公式(6)实施校正。实施P参数校正后即可得到正确的、两根射线出射到地表的斜率信息PS*、PR*。至此,即可得到运动学不变量。
1.3 低频宏观速度建立方法非一次反射波的运动学信息对于立体层析而言完全是噪音,而通过人工拾取数据点位置可以避开这些干扰,这也是运动学反偏移的一大特点。考虑需要适当的人工干预,立体层析在实际应用中由两步法构成:首先,通过自动拾取获得一个较为满意的初始速度模型,其好处是效率高;再根据人工干预在成像域拾取感兴趣的数据点,通过运动学反偏移去除与非一次反射波有关的数据点,进一步提升立体层析反演的精度。本文即通过该两步法获得了较高精度的速度场,为储层反演建立高质量的低频模型提供了可能。
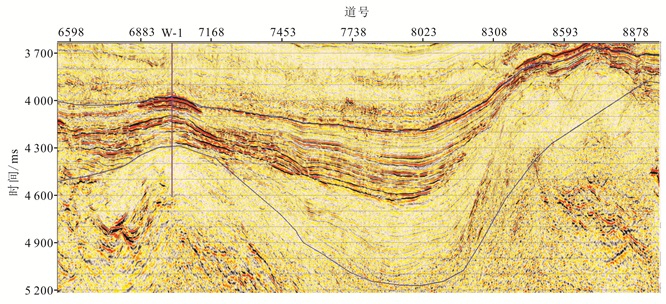
2 南海深水实际应用在我国南海深水区,钻井成本非常高,钻井数量有限,因此单纯依靠井资料建立速度模型是不现实的。更为困难的是,研究区目的层地层埋深起伏较大,如果没有一个较准确的初始模型,则反演结果的横向准确性将受到极大挑战。从南海深水区过W构造(背斜)的地震剖面(图 2)可以看到,受古地形特征影响,目的层珠海组(图中蓝色解释层位之间)埋深差异较大。在珠海组上段为一套连续性很好的强振幅地震反射层,并且左侧构造高部位(W-1井位置处)已经过钻井证实为一套优质储层。但是,随着埋深的加大,在珠海组下段地震反射振幅能量迅速衰减,整体呈现出低频、弱振幅反射特征,受常规反演低频模型补偿方法的限制,反演结果很难清晰地体现储层特征。为此,按照前文提出的思路,我们首先构建精确的速度模型。
|
| 图 2 目标区地震剖面 Figure 2 Seismic data in target area |
|
|
本文选用的二维测线长150 km,共3 404炮,最大偏移距8 275 m,最小偏移距200 m,炮间距50 m,检波点间距25 m。首先进行数据域立体层析反演处理。如前所述,数据域立体层析中拾取数据的精度十分重要。为保证拾取的精度,反演之前的数据做了精细的前期处理,如:各种噪音的去除、多次波压制、提高分辨率等处理,确保拾取前的数据具有较高的信噪比和精度。
梯度平方结构张量算法的效率非常高,本次反射波拾取偏移距范围为200~5 275 m,每隔200 m进行一次拾取,纵向时间范围不超过8 s。
图 3展示了数据域立体层析算法迭代中的一些中间结果。图 3a、b、c、d分别展示了为第1、5、6、16次迭代更新后的速度场,可以看出,随着迭代次数的增加,反演结果逐渐收敛。观察16次迭代后的倾角条(DIP-BAR)形态可以看出,反演结果已能较好地展示地下构造形态;故将数据域的第16轮迭代结果作为成像域层析的初始模型使用。

|
| a.第1次迭代更新后;b.第5次迭代更新后;c.第6次迭代更新后;d.第16次迭代更新后。 图 3 数据域立体层析迭代反演 Figure 3 Three-dimensional tomographic velocity inversion in data domain |
|
|
在实施成像域立体层析之前,如文献[21]所述,需要将共偏移距成像剖面的构造倾角与共成像点道集的剩余深度曲率特征提取出来。在实际处理中,实施成像域立体层析的具体步骤为:第一步,在经过去噪处理的地震道集上生成垂直速度谱;第二步,在叠前道集和叠加剖面上随机拾取一定数量的种子点作为输入的初始采样点;第三步,在叠加剖面上拾取构造倾角ξ,在CIG(共成像点道集)上拾取RMO信息;第四步,将前面拾取的信息进行如式(2)所示的运动学反偏移获得成像域立体层析所需的数据空间;第五步,对第四步获得的数据空间实施立体层析反演,待泛函下降到一定程度时即结束。
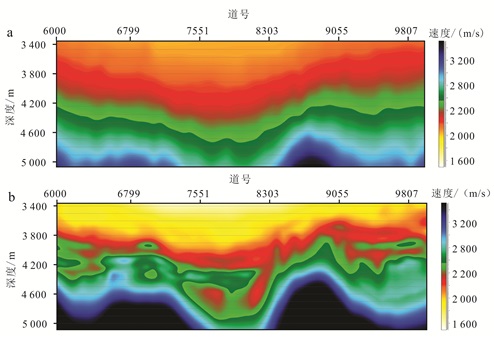
图 4为常规速度和成像域立体层析速度的比较,可以看到,成像域立体层析的速度剖面中显示出更多细节以及构造、岩性变化的纵、横向差异,地震速度谱的精度得到了显著提升。
|
| 图 4 常规速度(a)与成像域立体层析速度(b)比较 Figure 4 Comparison of normal (a) and three-dimensional tomographic (b) velocity |
|
|
在构建反演低频模型过程中,还要将速度谱信息与钻井实测的信息进行反复比较,通过井上速度进一步标定速度谱,以期构建更为准确的速度模型。
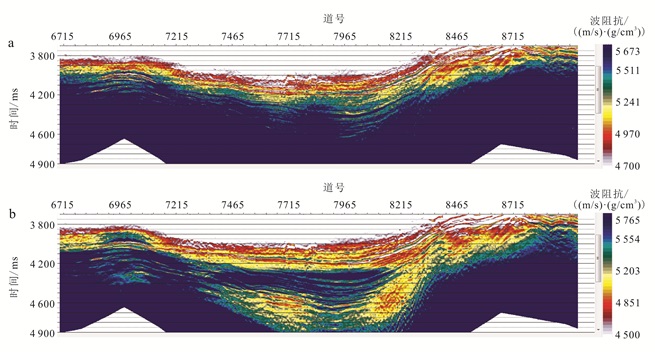
最后,利用上述速度谱分别构建低频模型进行反演,反演结果如图 5所示。从图 5a可以看到,基于常规速度谱反演的波阻抗结果遵循了基于地震反演波阻抗的规律,珠海组上段波阻抗能量值强、连续性好;但珠海组下段波阻抗反演结果精度非常差,难以反映地下真实沉积情况。图 5b为基于如图 4b所示立体层析速度剖面反演的波阻抗剖面,在珠海组下段反演出较为明显的低波阻抗砂体,符合珠海组下段扇三角洲沉积规律。这种反演结果上巨大的差异变化,主要来自于低频模型是否能够准确构建。
|
| a.基于常规速度反演的波阻抗;b.基于成像域立体层析速度反演的波阻抗。 图 5 反演结果比较 Figure 5 Comparison of impedance inversion results |
|
|
1) 波阻抗反演过程中的一个重要步骤就是补充地震资料中所缺失的低频信息,因此,能否构建准确的低频模型是制约反演结果准确性的核心。
2) 鉴于常规地震资料处理过程中速度谱精度低的缺陷,本文提出了一种基于两步法立体层析反演策略获得高精度低频宏观背景模型的思路,通过多次迭代计算,可以有效提高背景速度的精度,再通过与井资料的标定,构建出反演过程中的低频模型,进而获得较好的反演结果。
3) 该方法特别适用于我国南海深水区少井、无井的勘探区域,在地层起伏较大、地层压力变化较大的区域效果尤为明显。
| [1] |
栾颖, 冯晅, 刘财, 等. 波阻抗反演技术的研究现状及发展[J].
吉林大学学报(地球科学版), 2008, 38(11): 94-98.
Luan Ying, Feng Xuan, Liu Cai, et al. The Research Present and Future of Wave Impedance Inversion Technique[J]. Journal of Jilin University (Earth Science Edition), 2008, 38(11): 94-98. |
| [2] |
许艳秋, 文晓涛. 低频信息对阻抗反演的影响分析[J].
物探化探计算技术, 2015, 37(1): 78-82.
Xu Yanqiu, Wen Xiaotao. Effect Analysis of Low Frequency on Acoustic Impedance Inversion[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2015, 37(1): 78-82. |
| [3] |
叶云飞, 崔维, 张益明, 等. 低频模型对波阻抗反演结果定量解释的影响[J].
中国海上油气, 2014, 26(6): 32-36.
Ye Yunfei, Cui Wei, Zhang Yiming, et al. Impacts of Low-Frequency Models on the Quantitative Interpretation of Acoustic Impedance Inversion[J]. China Offshore Oil and Gas, 2014, 26(6): 32-36. |
| [4] |
叶云飞, 刘春成, 刘志斌, 等. 地质统计学反演技术研究与应用[J].
物探化探计算技术, 2014, 36(4): 1-6.
Ye Yunfei, Liu Chuncheng, Liu Zhibin, et al. Study and Application of Geostatistic Inversion[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2014, 36(4): 1-6. |
| [5] |
撒利明, 杨午阳. 地震反演技术回顾与展望[J].
石油地球物理勘探, 2015, 50(1): 184-201.
Sa Liming, Yang Wuyang. Past, Present, and Future of Geophysical Inversion[J]. Oil Geophysical Prospecting, 2015, 50(1): 184-201. |
| [6] |
乐友喜, 黄建良. 地质模型约束下的地震储层预测技术及其在梨树断陷中的应用[J].
吉林大学学报(地球科学版), 2013, 43(2): 632-640.
Le Youxi, Huang Jianliang. Seismic Reservoir Prediction Technology Constrained by Geology Model and the Application in Lishu Fault Depression[J]. Journal of Jilin University (Earth Science Edition), 2013, 43(2): 632-640. |
| [7] |
杨勤勇, 韩立国. 井间资料约束下地震波阻抗反演方法研究[J].
吉林大学学报(地球科学版), 2006, 36(3): 468-473.
Yang Qinyong, Han Liguo. Cross well Seismic Constrained Acoustic Impedance Inversion[J]. Journal of Jilin University (Earth Science Edition), 2006, 36(3): 468-473. |
| [8] | Pillet S W R, Brechet E, Mesdag P, et al. The Quest for the Low Frequencies in Pre-Stack Inversion[C]//2007 SEG Annual Meeting. Antonio: SEG, 2007. |
| [9] | Masoomzadeh H, Barton P J, Singh S C. Preservation of Low Frequencies in Wide-Angle Data Processing for Sub-Basalt Imaging[C]//2006 SEG Annual Meeting. New Orleans: SEG, 2006. |
| [10] | Deutsch C V, Andre G. GSLIB:Geostatistical Soft-ware Library and User's Guide[M]. Oxford: Oxford University Press, 1998. |
| [11] | Connolly P. Elastic Impedance[J]. The Leading Edge, 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [12] | Nivlet P. Low-Frequency Constrain in a Priori Model Building for Stratigraphic Inversion[C]//2004 SEG Annual Meeting. Denver: SEG, 2004. |
| [13] | James L S. Turning-Ray Tomography Using a Low-Spatial-Frequency Model Parameterization[J]. Geophysics, 2008, 73(5): 93-100. DOI:10.1190/1.2969109 |
| [14] | Mejer H T, Mosegaard K, Pedersen-Tatalovic R, et al. Attribute-Guided Well-Log Interpolation Applied to Low-Frequency Impedance Estimation[J]. Geophysics, 2008, 73(6): R83-R95. DOI:10.1190/1.2996302 |
| [15] | Behrens R A, Macleod M K, Tran T T, et al. Incorporating Seismic Attribute Maps in 3D Reservoir Models[J]. SPE Reservoir Evaluation & Engineering, 1998, 1(2): 122-126. |
| [16] | Pedersen-Tatalovic R, Uldall A, Lange Jacobsen N, et al. Event-Based Low-Frequency Impedance Modeling Using Well Logs and Seismic Attributes[J]. The Leading Edge, 2008, 27(5): 592-603. DOI:10.1190/1.2919576 |
| [17] | Billette F, Lambare G. Velcity Macro-Model Esti-mation from Seismic Reflection Data by Stereotomography[J]. Geophysical Journal International, 1998, 135(2): 671-690. DOI:10.1046/j.1365-246X.1998.00632.x |
| [18] | Lambare G. Stereotomgraphy[J]. Geophysics, 2008, 73(5): 25-34. |
| [19] |
倪瑶, 杨锴, 陈宝书. 立体层析反演方法理论分析与应用测试[J].
石油物探, 2013, 52(2): 121-131.
Ni Yao, Yang Kai, Chen Baoshu. Stereotomography Inversion Method:Theory and Application Testing[J]. Geophysical Prospecting for Petroleum, 2013, 52(2): 121-131. |
| [20] |
李振伟, 杨锴, 倪瑶, 等. 基于立体层析反演的偏移速度建模应用研究:以南海某二维深水地震数据为例[J].
石油物探, 2014, 53(4): 444-452.
Li Zhenwei, Yang Kai, Ni Yao, et al. Migration Velocity Analysis with Stereo-Tomography Inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 444-452. |
| [21] |
王宇翔, 杨锴, 杨小椿, 等. 基于梯度平方结构张量算法的高密度二维立体层析反演[J].
地球物理学报, 2016, 59(1): 263-276.
Wang Yuxiang, Yang Kai, Yang Xiaochun, et al. A High-Density Stereo-Tomography Method Based on the Gradient Square Structure Tensors Algorithm[J]. Chinese Journal of Geophysics, 2016, 59(1): 263-276. DOI:10.6038/cjg20160122 |
| [22] |
王宇翔, 杨锴, 杨小椿, 等. 基于运动学反偏移重建立体层析数据空间的理论与实践[C]//中国石油学会2015年物探技术研讨会论文集. 宜昌: [s. n. ], 2015: 346-349.
Wang Yuxiang, Yang Kai, Yang Xiaochun, et al. Theory and Practice of Reconstructing Stereoscopic Data Space Based on Kinematic Demigration[C]//The Proceedings of the Chinese Society of Petroleum Science and Technology 2015. Yichang: [s. n. ], 2015: 346-349. |


