2. 中国电力工程顾问集团东北电力设计院有限公司, 长春 130021;
3. 页岩油气富集机理与有效开发国家重点实验室, 北京 100083;
4. 中国石化页岩油气勘探开发重点实验室, 北京 100083;
5. 中国石化石油勘探开发研究院, 北京 100083
2. Northeast Electric Power Design Institute Co., Ltd. of China Power Engineering Consulting Group, Changchun 130021, China;
3. State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development, Beijing 100083, China;
4. SinoPEC Key Laboratory of Shale Oil/Gas Exploration and Production Technology, Beijing 100083, China;
5. SinoPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China
0 引言
页岩储层中的非常规资源已经成为油气勘探的研究热点。页岩结构复杂,内部物质的不均匀分布和定向排列使其通常表现出各向异性;可以通过研究页岩储层内部结构属性和各向异性的联系,为识别和勘探富含油气区域提供依据。
岩石物理模型是建立页岩微观结构与各向异性联系的常用工具[1-2]。但页岩各向异性受多种因素影响,包括黏土矿物的定向排列、非球形孔隙、微裂隙和裂缝属性[3]。黏土矿物定向排列是由页岩的压实作用引起的,不同程度的压实会引起黏土矿物不同的排列状态,进而影响各向异性。Hornby等[4]和Sayers[5]使用方位分布函数(ODF)来模拟黏土矿物的方位分布状态,然后使用各向异性微分等效介质模型(DEM)来估计页岩各向异性。Sayers[6]和Bandyopadhyay[3]指出非球形孔隙是页岩各向异性的另一个来源。Kwon等[7]发现页岩中裂隙的形状、大小和定向排列影响各向异性。Chapman模型[8]使用了多尺度孔隙系统,包括球形孔隙、裂隙和裂缝,并假设各向异性只来源于水平排列的裂缝。Jiang等[9]建立了一个双孔隙系统模型,即结合自相容等效介质理论(SCM)和Chapman模型来克服Chapman模型中不包含非球形孔隙的缺点,并将该模型应用于Haynesville页岩。
对于裂缝型页岩储层,各向异性由裂缝属性主导。本文在岩石物理建模过程中参照Jiang等[9]的工作,使用双孔隙系统模型以准确描述页岩的孔隙系统,并针对实际研究区域对该模型进行校正。由于模型的复杂性,反演需要确定非球形孔隙度、孔隙纵横比和裂缝密度,因此反演过程使用模拟退火优化粒子群算法(SA-PSO)[10]。作为一种智能寻优算法,它能够快速准确地寻找到各参数最优解,适用于复杂的非线性反演问题。该算法被应用到位于中国西南部的龙马溪组页岩,估计了该储层物性参数,如非球形孔隙度、孔隙纵横比、裂缝密度和各向异性参数。
1 岩石物理模型横向各向同性(TI)页岩的各向异性属性可以由Thomsen[11]各向异性参数表示:
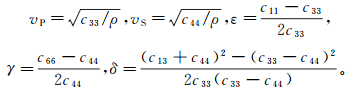 (1)
(1) 式中:cij是刚度张量分量,由岩石内部属性决定;vP、vS和ρ分别是纵波速度、横波速度和密度;ε、γ、δ是各向异性参数。岩石物理模型能够描述岩石内部属性并得到等效弹性张量,然后使用实测纵、横波速度对模拟结果进行校准。
包络体理论是页岩建模的一种常用方法。该理论把岩石中的组分当作不同形状的包含物,形状由纵横比决定。SCM[12]是一种各向同性包络体理论,能够结合多种矿物和孔隙类型构建等效介质模型,等效体积模量Ksc和等效剪切模量μsc由下式给出:
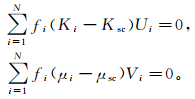 (2)
(2) 式中:N是组分数目;fi是每种组分的体积分数;Ki和μi是每种组分的体积模量和剪切模量;Ui和Vi是几何因子,由纵横比和模量决定,具体公式由Berryman[13]给出。图 1显示了SCM模型中不同孔隙纵横比(α)和孔隙度(φ)下vP和vS的变化情况。所用基质是黏土,颗粒纵横比为0.1,孔隙为水饱和。由图 1可见:随着α的增加,vP和vS逐渐增大;而随着φ的增加,vP和vS都变小。
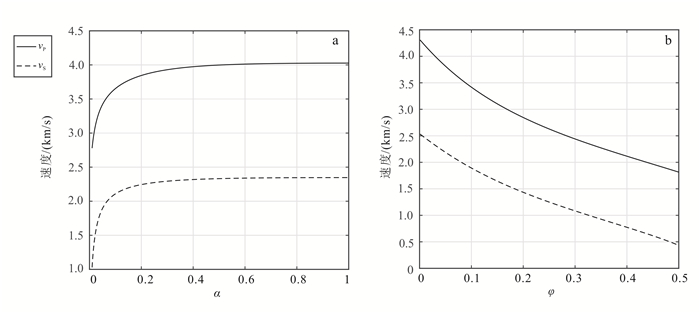
|
| a.φ=0.1;b. α=0.05。 图 1 SCM模型中纵、横波速度随孔隙纵横比和孔隙度的变化情况 Figure 1 Modeled P- and S- velocities as a function of pore aspect ratio and porosity by using SCM |
|
|
Chapman多尺度孔隙模型[8]可用来描述流体喷射流动现象对岩石等效模量的影响。波长小于孔隙尺寸的波在岩石中传播时会产生压力梯度,喷射流动是指由此产生的流体相互作用[14]。该模型考虑了频率和孔隙压力的影响,适用于各向同性和各向异性介质[9]。Chapman模型认为岩石包含球形孔隙、裂隙和裂缝。图 2是该模型的示意图[15],其中球形孔隙和裂隙随机分布,裂缝水平排列,各向异性由裂缝引起。除了裂缝与裂缝之间,球形孔隙、裂隙和裂缝相互连通来保证流体的流动性[8]。Chapman模型中的孔隙度(φchap)可表示为球形孔隙度(φrp)、裂隙孔隙度(φc)和裂缝孔隙度(φf)三者之和:
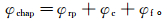 (3)
(3) 裂隙和裂缝被认为是理想椭球体,具有相同的纵横比,因此裂隙密度(εc)和裂缝密度(εf)由下式得出:
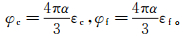 (4)
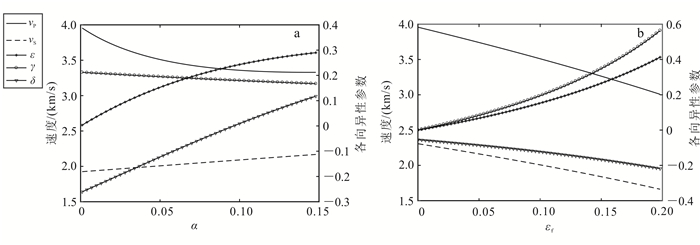
(4) Chapman模型的具体公式由Jiang等[9]总结给出。模型中参数都有相应的物理意义,并且大部分可以直接测定或通过测定值估计得到。图 3a是孔隙纵横比对各向异性参数的影响。由图 3a可见:vS、ε和δ随着α的增大而增大,其中δ的变化最大;而vP和γ却随着α的增大而减小。图 3b为各向异性参数随裂缝密度的变化。由图 3b可见:vP、vS和δ随着εf的增大而减小;而ε和γ却随着εf的增大而增大,其中γ变化最大。模型所用基质是黏土,孔隙为水饱和。
|
| a. εf=0.1,φ=0.1,εc=0.025;b. α=0.05,φ=0.1,εc =0.025。 图 3 Chapman模型得到的各向异性参数随孔隙纵横比和裂缝密度的变化情况 Figure 3 Modeled anisotropy parameters as a function of pore aspect ratio and fracture density by using Chapman's model |
|
|
Chapman模型中孔隙被认为是球形,但大部分页岩包含非球形孔隙。Jiang等[9]将SCM和Chapman模型相结合构建了双孔隙系统模型来估计Haynesville页岩的储层属性。在建模过程中,SCM模型用来描述矿物和非球形孔隙,非球形孔隙间相互不连通。Chapman模型包含球形孔隙、裂隙和裂缝,其中裂缝间相互不连通,裂隙和球形孔隙至少与一个裂缝相连通,用来描述流体喷射流动现象对岩石等效模量的影响。该双孔隙系统模型将总孔隙度(φ)划分为非球形孔隙(φnp)和Chapman模型孔隙系统,这两个孔隙系统相互不连通,可表示为
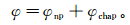 (5)
(5) 使用SCM模型时需要考虑各包络体的纵横比,本文中黏土矿物纵横比是0.10,脆性矿物,例如石英、方解石、黄铁矿等是1.00,干酪根是0.01。SCM模型中影响速度的主要因素是孔隙形状,在建模流程中,SCM模型中的非球形孔隙与Chapman模型孔隙系统中的裂隙和裂缝有相同的纵横比,且非球形孔隙尺寸与矿物颗粒以及球形孔隙、裂隙尺寸一致[9]。裂缝尺寸对喷射流动现象影响很大,通常可通过岩心数据确定。
双孔隙系统页岩岩石物理建模流程由图 4给出。建模过程中,首先使用SCM模型构建包含矿物和非球形孔隙的各向同性基质,矿物和孔隙在该基质中均匀并且随机方位分布且孔隙互不连通。然后使用Chapman模型向该基质中加入球形孔隙、裂隙和裂缝的影响,其中裂隙的方位随机,裂缝呈水平排列,最终得到各向异性页岩模型。在该岩石物理模型中:各向异性来源于水平裂缝,主要受孔隙纵横比和裂缝密度影响;而各向同性基质的纵、横波速度受非球形孔隙度和孔隙纵横比影响;Chapman模型中其他参数可根据实际数据给定。图 5是岩石物理模型中非球形孔隙度、纵横比、裂缝密度这3个重要储层参数对各向异性参数的影响,所用基质是黏土,孔隙是水饱和。其中:φnp对vS和γ的影响较大;α较小时对各向异性参数的影响大,但随着α增加,影响逐渐减小;εf的取值对各向异性参数的影响始终较大。
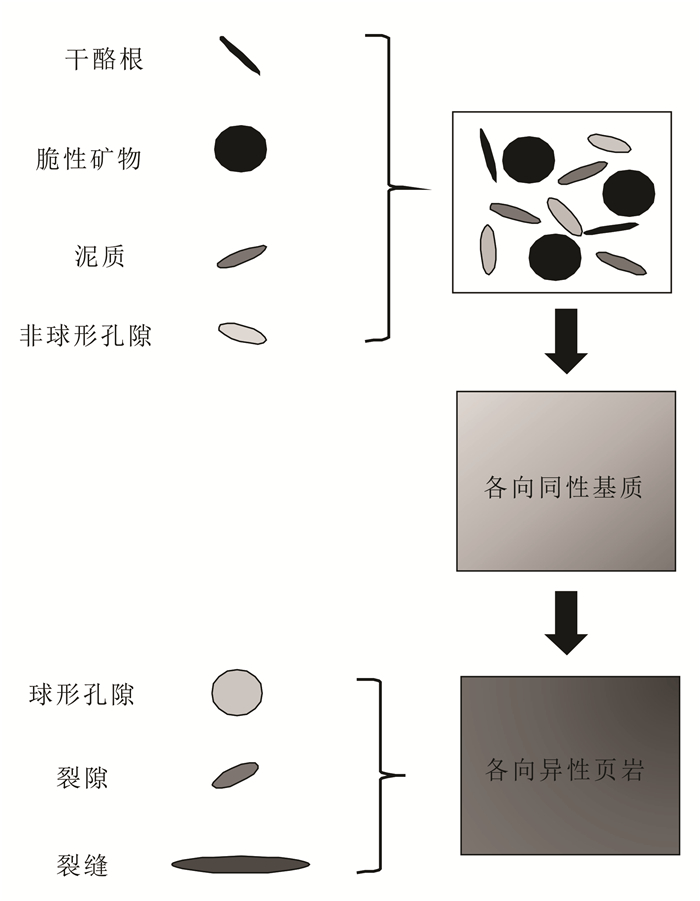
|
| 图 4 页岩岩石物理模型 Figure 4 Rock physics model for shale |
|
|
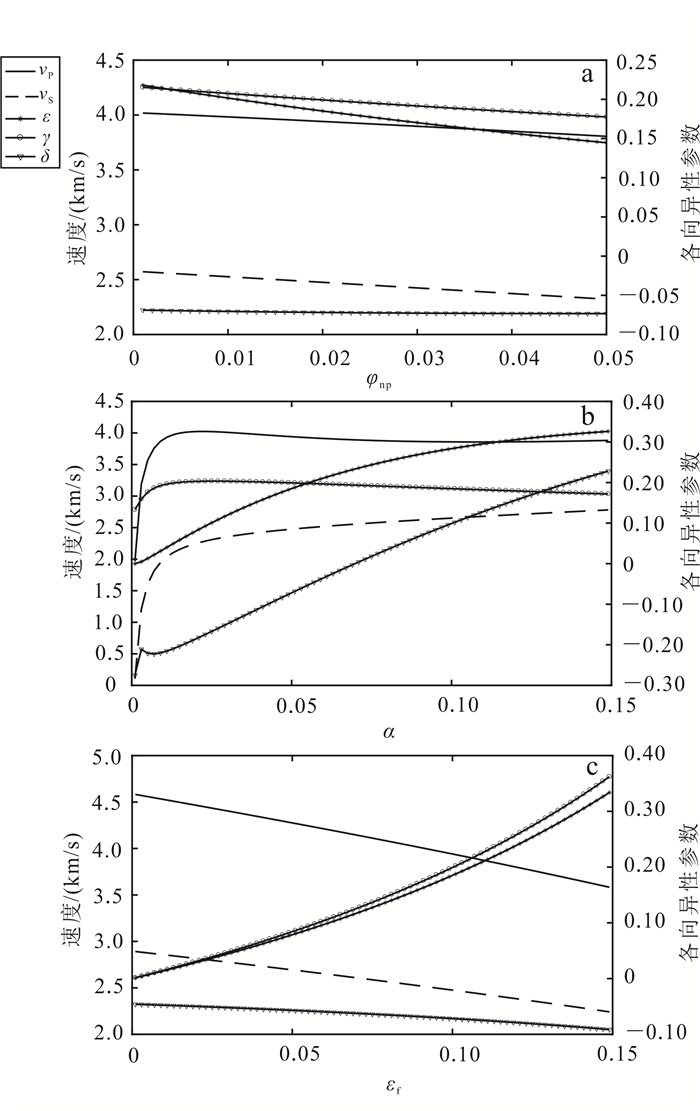
|
| a. α =0.05,φ=0.1,εf =0.1,εc=0.025;b. φnp=0.02,φ=0.1,εf=0.1,εc=0.025;c. φnp=0.02,α =0.05,φ=0.1,εc=0.025。 图 5 岩石物理模型中各向异性参数随非球形孔隙度、孔隙纵横比和裂缝密度的变化情况 Figure 5 Modeled anisotropy parameters as a function of non-spherical porosity, pore aspect ratio and fracture density by using the rock physics model |
|
|
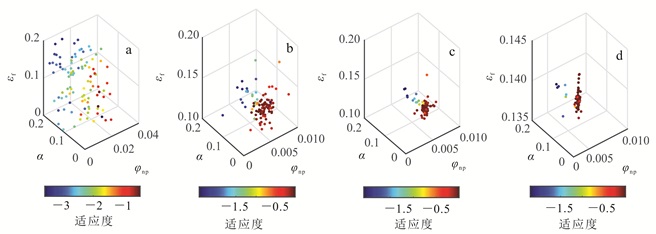
研究对象是位于中国西南四川盆地的龙马溪组页岩。测井数据在图 6中显示,包括伽马射线、纵横波速度、密度、孔隙度和组分信息。目标层段页岩致密,孔隙度较低,干酪根和黏土含量高。岩心资料显示该层段水平裂缝发育,裂缝尺寸平均值是100 μm。
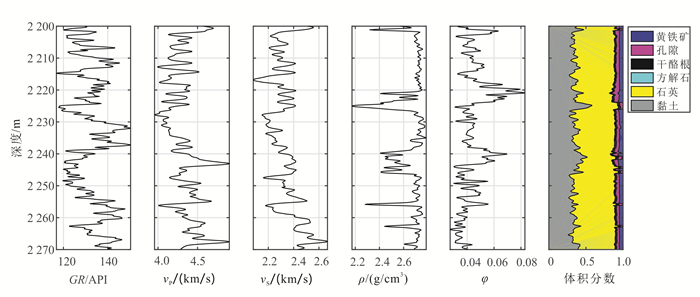
|
| GR.自然伽马。 图 6 页岩测井数据 Figure 6 Shale information from the well data |
|
|
目标层段是包含水平裂缝的横向各向同性(TI)页岩。邓继新等[16]对龙马溪组页岩微观结构的研究发现:该页岩的孔隙类型包含原生孔隙、次生孔隙和裂隙,各种孔隙尺度不同,但大部分小于2 μm;孔隙大部分是非球形孔隙,且呈孤立分布,连通性差。
岩石物理模型中参数众多,部分参数可由前人研究给定。Guo等[17]直接使用了Chapman[8]给出的频率和弛豫时间参数值。Jiang等[9]使用双孔隙系统模型对Haynesville页岩储层参数进行了估计。龙马溪组页岩类比于Haynesville页岩,两者主要矿物组分都是黏土、石英和方解石,孔隙度和渗透性都很低,并且都具有横向各向同性,因此认为两者具有相似性。据此,我们为岩石物理建模过程中部分参数赋予了相同值。其中:Chapman模型中频率(f)取10 kHz,接近测井频率;非球形孔隙、球形孔隙、裂隙的尺寸(ξ)相同,取1 μm;裂隙密度由裂缝密度得到,
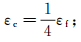 (6)
(6) 水饱和裂隙的弛豫时间(τm)由Chapman[8]给出;而裂缝的弛豫时间(τf)由它们的尺寸(af)决定,
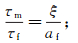 (7)
(7) 矿物和流体的模量和密度由表 1给出。最终,岩石物理模型中的未知参数可确定为非球形孔隙度、孔隙纵横比和裂缝密度。通过使用测量得到的纵、横波速度可反演得到这3个储层参数,进而估计页岩各向异性。
| 体积模量/GPa | 剪切模量/GPa | 密度/(g/cm3) | |
| 黏土 | 26.0 | 16.0 | 2.55 |
| 干酪根 | 2.9 | 2.7 | 1.30 |
| 石英 | 38.0 | 44.0 | 2.65 |
| 方解石 | 77.0 | 32.0 | 2.71 |
| 黄铁矿 | 147.0 | 132.0 | 4.93 |
| 水 | 2.8 | 0 | 1.09 |
反演目标函数通常可写作
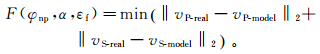 (8)
(8) 式中:vP-real和vS-real是纵、横波速度的测量值;vP-model和vS-model是由岩石物理模型计算的纵、横波速度。
传统反演方法基于遍历搜索,即将各参数取值空间划分成n个区间,遍历各参数的各取值区间来寻找满足目标函数的值[18]。对于本文中的三参数反演问题,传统方法需要迭代n3次。岩石物理模型复杂,若区间数过多则计算量大,过少则无法找到最优解。而且,多参数反演存在多解性,需要加入更多反演约束条件来减少多解性。地震反演方法通常在目标函数中加入约束项来减少多解性,李坤等[19]使用平滑模型作为约束项来减少地震反演中低频趋势的多解性。本文考虑到实际储层属性存在垂向连续性、各深度点储层参数并不完全独立,在目标函数中加入平滑约束项后为
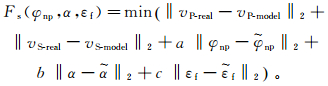 (9)
(9) 式中:a、b、c是各参数平滑项的权值;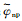
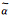
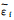
基于岩石物理模型和模拟退火优化粒子群算法的页岩储层参数反演流程(图 7)如下。
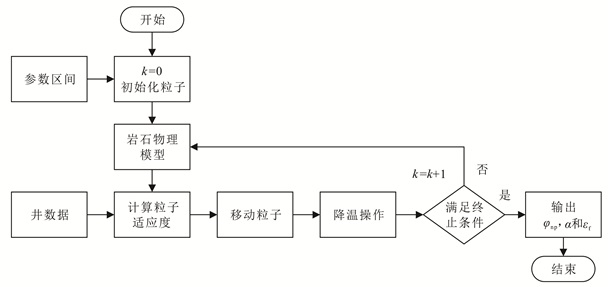
|
| 图 7 基于岩石物理模型和模拟退火优化粒子群算法的页岩储层参数反演流程 Figure 7 Workflow for rock properties inversion by using shale rock physics model and SA-PSO |
|
|
1) 初始化参数。从参数取值区间抽取M个随机点,被称作粒子:
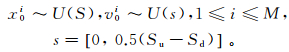 (10)
(10) 式中:x0i和v0i是第i个粒子的初始化位置和速度,位置也代表参数的取值,粒子可以是多维的,每个维度对应一个参数;U表示从区间等概率取值;S是参数取值区间;Su和Sd是S的上下界;s是速度初始化区间。初始化退火温度T0应足够大,取T0=10 000。
本问题中3个储层参数的取值范围分别是:
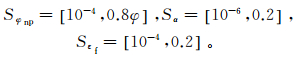 (11)
(11) 2) 计算粒子适应度。
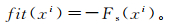 (12)
(12) 式中:fit是粒子适应度函数,由目标函数值决定;xi为粒子位置。
3) 移动粒子。
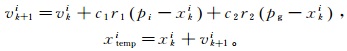 (13)
(13) 式中:学习因子c1和c2是非负常数,且c1+c2=4.1;r1和r2是属于[0, 1]的随机数;xki和vki是第k次迭代时粒子的位置和速度;vk+1i指经过本次迭代后粒子的速度;pg是全局最优值,指本次迭代时所有粒子中适应度值最大的粒子所在位置;pi是个体最优值,指单个粒子移动至今适应度最大时的位置;xitemp是本次迭代后粒子位置的可能取值。若满足式(14)中的任何一个,则粒子移动到位置xitemp;否则粒子位置不变。
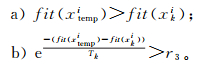 (14)
(14) 式中:Tk是当前温度;r3是属于[0, 1]的随机数。
4) 降温操作。
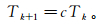 (15)
(15) 式中,c是降温系数,取0.93。
5) 重复步骤2)至4)直到满足收敛条件。
对目标层段进行反演,使用100个粒子,迭代60次。图 8展示了一个深度点处的反演迭代收敛过程。由图 8可以看出,粒子的适应度由低变高,并且逐渐聚集到最优解处。最优解满足目标函数公式(9),此时粒子在三维参数空间的位置也就是各参数的取值。如果传统方法中每个参数区间划分50份,则需要迭代125 000次,而模拟退火优化粒子群算法共需迭代6 000次,计算量得以大大降低。
|
| a.初始化后粒子状态;b.迭代20次后;c.迭代40次后;d.迭代60次后。 图 8 模拟退火优化粒子群算法收敛过程 Figure 8 Optimization procedure of SA-PSO |
|
|
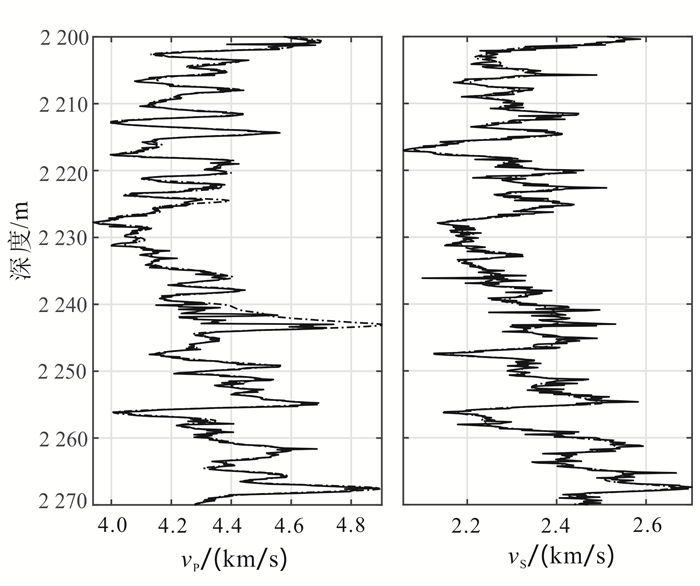
图 9是目标层段使用模型计算出的纵、横波速度值和实测值,两者拟合很好,表明了本文方法的准确性。图 10是反演得到的储层参数曲线,可清楚地看出储层参数随深度的变化趋势,并首次提供了该研究区域的非球形孔隙度。Qian等[20]对龙马溪组页岩的研究表明,该层段孔隙纵横比较小,平均低于0.05,与本文反演值(图 10)一致。Jiang等[9]对Haynesville页岩的研究给出它的裂缝密度是0.04,由于本文目标层裂缝发育,反演值较高(图 10)。图 11是估计的各向异性参数,其中ε和γ具有强相关性,而γ和δ在部分区域出现负相关;该现象与Bandyopadhyay[3]及Sayers[6]的研究一致。目标层段各向异性参数γ总体大于ε,并且δ为负值;Qian等[20]的研究也给出了相似的结果,但目标层各向异性强度由于裂缝发育而更大。
|
| 图 9 纵、横波速度计算值(实线)和实测值(虚线) Figure 9 Modeled (solid) and measured (dashed) P- and S-wave velocities |
|
|
|
| 图 10 目标层段储层参数反演结果 Figure 10 Inversion result of the formation properties |
|
|
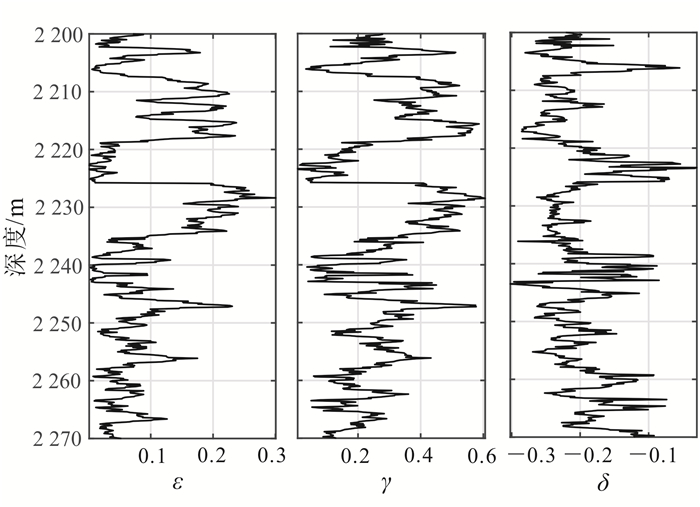
|
| 图 11 目标层各向异性参数反演结果 Figure 11 Inversion result of the anisotropy parameters |
|
|
本文使用改进的岩石物理模型和模拟退火优化粒子群算法对页岩裂缝属性和各向异性进行了反演。岩石物理建模为使用等效介质模型和Chapman模型相结合建立的双孔隙系统模型,以准确地描述页岩微观孔隙结构,反演过程使用智能算法准确求解复杂岩石物理模型下三参数反演问题。将方法应用到龙马溪组页岩气储层,反演结果与实测数据和已有研究结果相匹配,说明了本文方法的有效性。
本文的研究为页岩储层的描述提供了更多的有效信息。页岩结构复杂,影响各向异性的因素很多,进一步的研究需要使用更加准确复杂的岩石物理模型进行模拟。而求解复杂岩石物理模型,反演方法同样需要进一步提高。
| [1] |
张广智, 陈娇娇, 陈怀震, 等. 基于岩石物理模版的碳酸盐岩含气储层定量解释[J].
吉林大学学报(地球科学版), 2015, 45(2): 630-638.
Zhang Guangzhi, Chen Jiaojiao, Chen Huaizhen, et al. Quantitative Interpretation of Carbonate Gas Reservoir Based on Rock Physics Template[J]. Journal of Jilin University (Earth Science Edition), 2015, 45(2): 630-638. |
| [2] |
逄硕, 刘财, 郭智奇, 等. 基于岩石物理模型的页岩孔隙结构反演及横波速度预测[J].
吉林大学学报(地球科学版), 2017, 47(2): 606-615.
Pang Shuo, Liu Cai, Guo Zhiqi, et al. Estimation of Pore-Shape and Shear Wave Velocity Based on Rock-Physics Modelling in Shale[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(2): 606-615. |
| [3] | Bandyopadhyay K. Seismic Anisotropy: Geological Causes and Its Implications to Reservoir Geophysics[D]. San Francisco: Stanford University, 2009. |
| [4] | Hornby B E, Schwartz L M, Hudson J A. Anisotropic Effective-Medium Modeling of the Elastic Properties of Shales[J]. Geophysics, 1994, 59(10): 1570-1583. DOI:10.1190/1.1443546 |
| [5] | Sayers C M. Anisotropic Velocity Analysis[J]. Geo-physical Prospecting, 1995, 43(4): 541-568. DOI:10.1111/gpr.1995.43.issue-4 |
| [6] | Sayers C M. Seismic Anisotropy of Shales[J]. Geo-physical Prospecting, 2005, 53(5): 667-676. DOI:10.1111/gpr.2005.53.issue-5 |
| [7] | Kwon O, Kronenberg A K, Gangi A F, et al. Per-meability of Illite-Bearing Shale:1. Anisotropy and Effects of Clay Content and Loading[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B10): 205-223. |
| [8] | Chapman M. Frequency-Dependent Anisotropy due to Meso-Scale Fractures in the Presence of Equant Porosity[J]. Geophysical Prospecting, 2003, 51(5): 369-379. DOI:10.1046/j.1365-2478.2003.00384.x |
| [9] | Jiang M, Spikes K T. Estimation of Reservoir Pro-perties of the Haynesville Shale by Using Rock-Physics Modelling and Grid Searching[J]. Geophysical Journal International, 2013, 195: 315-329. DOI:10.1093/gji/ggt250 |
| [10] |
高鹰, 谢胜利. 基于模拟退火的粒子群优化算法[J].
计算机工程与应用, 2004, 40(1): 47-50.
Gao Ying, Xie Shengli. Particle Swarm Optimization Algorithms Based on Simulated Annealing[J]. Computer Engineering and Applications, 2004, 40(1): 47-50. |
| [11] | Thomsen L. Weak Elastic Anisotropy[J]. Geophy-sics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [12] | O'Connell R J, Budiansky B. Seismic Velocities in Dry and Saturated Cracked Solids[J]. Journal of Geophysical Research, 1974, 79(35): 5412-5426. DOI:10.1029/JB079i035p05412 |
| [13] | Berryman J G. Mixture Theories for Rock Properties[M]. Washington, D C: American Geophysical Union, 1995: 205-228. |
| [14] | Dvorkin J, Nolen-Hoeksema R, Nur A. The Squirt-Flow Mechanism:Macroscopic Description[J]. Geophysics, 1994, 59(3): 428-438. DOI:10.1190/1.1443605 |
| [15] |
兰慧田. 裂缝性孔隙介质波场模拟与频变AVO储层参数反演[D]. 长春: 吉林大学, 2014.
Lan Huitian. Wave Field Modeling in Fractured Porous Media and Frequency-Dependent AVO Reservoir Parameters Inversion[D]. Changchun: Jilin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10183-1014268078.htm |
| [16] |
邓继新, 王欢, 周浩, 等. 龙马溪组页岩微观结构、地震岩石物理特征与建模[J].
地球物理学报, 2015, 58(6): 2123-2136.
Deng Jixin, Wang Huan, Zhou Hao, et al. Microtexture, Seismic Rock Physical Properties and Modeling of Longmaxi Formation Shale[J]. Chinese Journal of Geophysics, 2015, 58(6): 2123-2136. DOI:10.6038/cjg20150626 |
| [17] | Guo Z Q, Liu C, Liu X W, et al. Research on Anisotropy of Shale Oil Reservoir Based on Rock Physics Model[J]. Applied Geophysics, 2016, 13(2): 382-392. DOI:10.1007/s11770-016-0554-0 |
| [18] | Guo Z Q, Li X Y. Rock Physics Model-Based Prediction of Shear Wave Velocity in the Barnett Shale Formation[J]. Journal of Geophysics and Engineering, 2015, 12(3): 527-534. DOI:10.1088/1742-2132/12/3/527 |
| [19] |
李坤, 印兴耀, 宗兆云. 利用平滑模型约束的频率域多尺度地震反演[J].
石油地球物理勘探, 2016, 51(4): 760-780.
Li Kun, Yin Xingyao, Zong Zhaoyun. Multi-Scale Seismic Inversion in Frequency Domain Based on Smoothing Model[J]. Oil Geophysical Prospecting, 2016, 51(4): 760-780. |
| [20] | Qian K, Zhang F, Chen S, et al. A Rock Physics Model for Analysis of Anisotropic Parameters in a Shale Reservoir in Southwest China[J]. Journal of Geophysics and Engineering, 2016, 13(1): 19-34. DOI:10.1088/1742-2132/13/1/19 |