2. 页岩油气富集机理与有效开发国家重点实验室, 北京 100083;
3. 中国石化页岩油气勘探开发重点实验室, 北京 100083;
4. 中国石化石油勘探开发研究院, 北京 100083
2. State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development, Beijing 100083, China;
3. SinoPEC Key Laboratory of Shale Oil/Gas Exploration and Production Technology, Beijing 100083, China;
4. SinoPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China
0 引言
近年来,随着人们对油气资源需求量的增加,以及常规油气资源的不断减少,页岩油气的研究与勘探逐渐成为国内油气资源研究的热门领域。位于渤海湾盆地的济阳坳陷为富油气坳陷,其中沾化凹陷罗家地区泥页岩厚度大(1.0~1.5 m),裂缝发育良好,沙河街组三段(简称沙三段)中下部的油泥页岩为裂缝油气藏主要赋存区域[1-10]。在地震分析的过程中,将井震数据结合对储层特性进行研究十分重要。但由于测井资料与地震资料分辨尺度差异较大,将测井数据应用到地震响应计算中分析的方法并未得到充分的研究和应用。
为了将测井数据粗化到地震数据尺度,可采用Backus平均理论[11]对测井数据进行粗化,在长波长条件下将层状介质等效为VTI(vertical transversely isotropy)介质。Schoenberg等[12]将该理论推广到了一般的层状各向异性介质中;Kumar[13]将Backus平均理论应用到具有低对称各向异性的裂缝型页岩储层中。
地层中裂缝的发育引起地震波速度和反射振幅随方位角的变化,因此可根据地震响应的方位各向异性特征识别和描述裂缝属性。传统的AVO(amplitude versus offset)研究以Zoeppritz方程[14]为基础。由于Zoeppritz方程的复杂性,很多学者对其进行简化并应用于实际研究当中。Banik[15]和Thomsen[16]提出弱各向异性参数可以反映TI(transeversely isotropy)介质中反射界面两侧时差速度和反射振幅的变化。Rüger[17]基于Banik和Thomsen的研究,给出了方位各向异性介质在任意方位角、大入射角情况下的纵波反射系数近似公式。AVAZ(amplitude versus azimuth)分析研究地震子波经过界面反射后振幅随入射角和方位角的变化,通常是由一组垂直裂缝引起的各向异性。Sayers等[18]的研究表明,在地震勘探中,垂直裂缝的发育会引起更强更明显的AVAZ异常响应。Schoenberg等[19]于1999年应用传播矩阵算法[20]分析了裂缝储层中地震反射波与方位角相关的调谐效应。
地震正演模拟可以有效地观测地震波在各向异性介质中传播的规律和特点,主要方法有反射率法、有限差分法和射线追踪法,其中反射率法的精度高于其他两种方法。Fuchs等[21]最初提出将反射率法应用于各向同性层状介质地震响应的计算。Sheriff[22]对反射率法在各向同性介质中的应用进行了更详尽的论述。Booth等[23]将反射率法推广至各向异性层状介质的计算。Fryer等[24]给出了存在弹性水平对称面情况下的任意各向异性介质所对应的系统矩阵形式。Mallick等[25]通过反射率法计算得到方位各向异性层状介质的合成地震记录。
本文基于各向异性条件下的反射率法,结合Schoenberg传播矩阵法中水平慢度的表达方式和VTI各向异性介质中的相速度公式,推导出了针对上覆层为各向异性介质的反射率法,并模拟得到全波场地震AVAZ响应。然后结合罗家地区裂缝型页岩油储层测井资料,应用各向异性Backus平均理论进行井震匹配,并通过Schoenberg线性滑动理论[26]引入垂直裂缝建立岩石物理模型,将储层裂缝特征与地震响应较好地联系起来;再应用各向异性反射率法进行各向异性地震AVAZ响应模拟并获得方位振幅分布,由此来分析罗家地区页岩油储层的方位各向异性地震响应特征。
1 罗家地区各向异性页岩油储层测井数据分析罗家鼻状构造带北邻渤南洼陷,南靠陈家庄凸起,研究井L位于济阳坳陷沾化凹陷罗家鼻状构造带西翼。研究区域2 909.0~3 132.0 m为沙河街组三段中下部地层,发育厚层油泥岩、油页岩,地层能量充足,钻井过程中油气显示活跃。L井中矿物成分主要为方解石、黏土矿物和石英,同时含有少量白云石、黄铁矿、斜长石和钾长石等。图 1a为L井井区沙三段中下部地层矿物类型及体积分数示意图。可以看出,随着地层由老到新的变化,黏土矿物和石英的平均体积分数呈现逐渐增加的趋势,方解石和白云石的平均体积分数则呈现逐渐降低的趋势。

|
| 图 1 罗家地区L井页岩储层测井数据 Figure 1 Well log data from shale oil reservoir of Well L in Luojia area |
|
|
图 1b—f为L井页岩储层测井数据,在纵波速度、密度以及孔隙度曲线中存在明显的突变处,即深度3 060.0 m处:此界面以上地层的纵波速度与密度明显较低,孔隙度较高。这是由于富有机质页岩储层在常规测井曲线中具有一定的规律性,即高电阻率、高声波时差、低密度等特征,与其他非泥页岩层段之间具有较大区别,更易于进行识别。
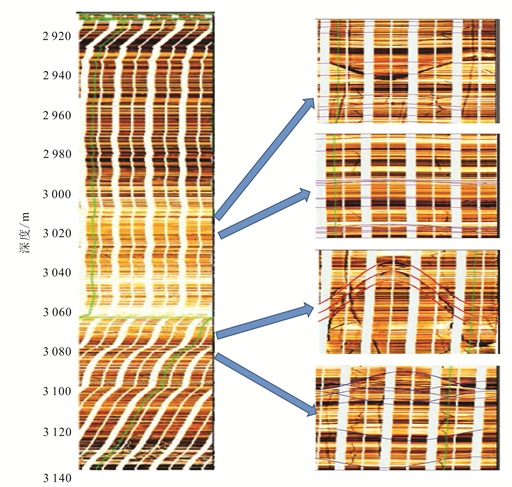
图 2为L井沙河街组三段下亚段的全井眼地层微电阻扫描成像(FMI, formation micro-resistivity scanning imaging)[27]测井结果。通过放大的FMI图像可以看出,该段地层内发育角度较低的层间缝和高角度的高导缝,且水平层理发育。地层的VTI各向异性主要由水平层理和层间缝引起;而高角度的高导缝为垂直裂缝,在VTI各向异性的背景下,垂直裂缝的存在使得页岩储层具有等效正交各向异性介质的特征,响应表现为方位各向异性特征。
|
| 图 2 罗家地区L井水平缝和垂直缝FMI成像结果 Figure 2 FMI images of horizontal fractures and vertical fractures of Well L in Luojia area |
|
|
Backus平均理论常用于测井数据中估算长波长条件下薄层的弹性性质。在长波长的条件下,对VTI各向异性介质应用Backus平均理论,得到的等效介质可以由复数模量描述为
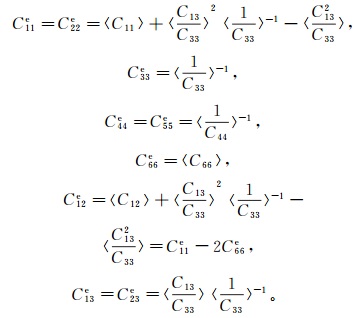 (1)
(1) 式中:Cij和Cije分别为Backus平均前、后等效介质的弹性刚度系数;〈·〉表示加权平均。
2.2 Schoenberg线性滑动理论Schoenberg等[26]提出当地层中同时存在水平层理和垂直裂缝时,在长波长条件下可等效为正交各向异性介质。该正交各向异性模型由两部分组成,第一部分为具有一个垂向对称轴的横向各向同性背景介质,第二部分是一组平行垂直裂缝。正交各向异性介质的刚度矩阵可以表示为
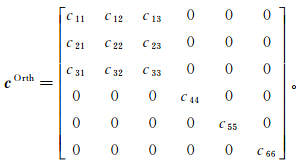 (2)
(2) 其中:
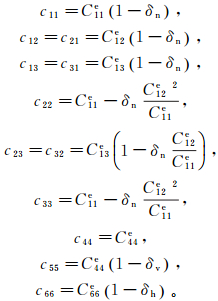 (3)
(3) 其中,无量纲量可定义为
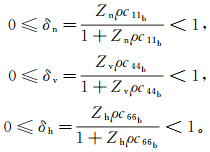 (4)
(4) 式中:Zn为法向柔度;Zv为垂向正切柔度;Zh为水平正切柔度。假设δv=δh,并利用裂缝密度e来估计δv,δh,δn:
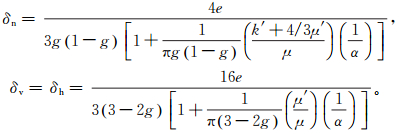 (5)
(5) 式中:g=(vS/vP)2,vS和vP分别为背景介质的S波和P波速度;孔隙纵横比α=3φ/4πe,φ是裂缝的体积分数;μ是背景介质的剪切模量;k′和μ′分别为裂缝中流体成分的体积模量和剪切模量。
2.3 各向异性反射率方法反射率方法可以模拟弹性或非弹性介质中地震波的反射透射问题,具有数值稳定性高、精度高、计算成本低的特点。
首先假设介质仅在垂向变化,且不存在体力。为了对运动方程变量进行分离,将动量方程和本构方程进行三维傅里叶变换:
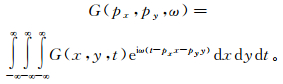 (6)
(6) 式中:ω为角频率;px、py为水平方向的慢度分量。G(x,y,t)表示笛卡尔坐标系下的动量方程和本构方程;t为时间。经过傅里叶变换后可得到微分方程系统[28]:
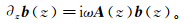 (7)
(7) 式中:A为6×6的系统矩阵;b为应力位移矢量,表示连续穿过水平面的变量,
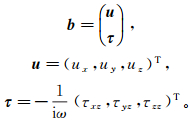 (8)
(8) 式中:ux,uy,uz是位移的分量;τxz,τyz,τzz是应力张量的z方向分量。由此而得到6×6的系统矩阵A可由水平慢度px和py、密度ρ以及弹性参数cij (i, j=1, 2, 3, …, 6)来表示。如果弹性参数与角频率无关,那么A与频率无关。
当目标模型的上半空间为各向异性时,水平慢度px和py可表示为
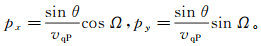 (9)
(9) 式中:θ为入射角;Ω为方位角;vqP为上部介质的纵波相速度。
在求解微分方程系统的过程中,可通过引入经典的传播算子法[28-29]来完成计算。传播算子P(z, z1)为微分方程系统的唯一连续解:
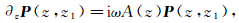 (10)
(10) 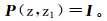 (11)
(11) 式中:I是6×6的单位矩阵。当在深度z1处选择b(z1)作为明确的边界条件时,那么深度为z处的响应为b(z)=P(z, z1)b(z1)。通过系统矩阵A的特征值矩阵和特征向量矩阵,可求得当能量自上而下入射时,各向异性层状介质的底界面反射、透射系数矩阵R:
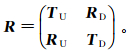 (12)
(12) 式中:TU、TD分别为3×3上行波和下行波透射系数矩阵;RU、RD分别为3×3上行波和下行波反射系数矩阵。
通过Fryer等[30]引入的散射算子和散射矩阵计算并整理,可以得到层状介质中第i+1层RDi+1、RUi+1、TDi+1、TUi+1和第i层RDi、RUi、TD、TUi之间的递归关系式[31]:
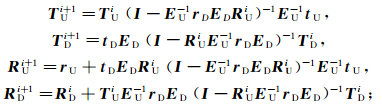 (13)
(13) 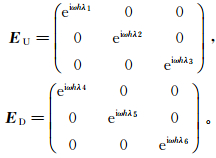 (14)
(14) 式中:rD、rU和tD、tU分别为界面深度z=zi+1处的反射矩阵和透射矩阵;h=zi+1-zi为深度差;λ为系统矩阵A的特征值。
计算反射响应是求取合成地震记录的第一步,由计算得到RD中的频率域反射响应rppD,与地震子波频谱F(ω)相乘后进行逆傅里叶变换,可得到时间域合成地震记录RppD:
 (15)
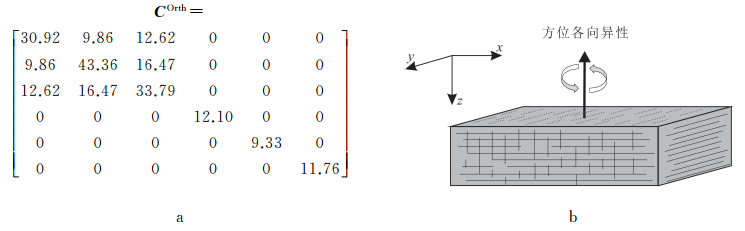
(15) 根据Schoenberg等[19]的正交各向异性理论,设计一个三层理论模型进行分析,模型参数如表 1所示,表中ε、γ、δ为各向异性参数。理论模型为三层正交各向异性介质,中间层复数刚度矩阵如图 3a所示。计算中用到的地震子波为40 Hz雷克子波。
| VTI介质 | vP/(km/s) | vS/(km/s) | ε | γ | δ | ρ/(g/cm3) | 厚度/m | e |
| 层1 | 4.2 | 2.7 | 0.20 | 0.10 | 0.3 | 2.49 | 50 | 0.1 |
| 层2 | 3.8 | 2.2 | 0.12 | 0.13 | 0.2 | 2.50 | 40 | 0.1 |
| 层1 | 4.2 | 2.7 | 0.20 | 0.10 | 0.3 | 2.49 | 50 | 0.1 |
|
| a.矩阵描述;b.模型描述。 图 3 正交各向异性介质示意图 Figure 3 Schematic of orthorhombic medium |
|
|
理论模型中的正交各向异性介质由两部分组成:VTI各向异性背景介质以及垂直裂缝系统,如图 3b所示。研究方位各向异性特征时,规定观测面垂直于模型中的垂直裂缝发育面;当模型中仅具有VTI各向异性时,地震响应表现为方位各向同性,引入垂直裂缝后地震响应则具有方位各向异性。正交各向异性介质的地震响应不仅与背景介质的VTI各向异性参数有关,也与垂直裂缝密度有关,因此本文在计算中固定裂缝密度值为0.1。
依据各向异性反射率理论,大入射角处方位各向异性特征明显,但临界角处会发生全反射,因此选取入射角30°的地震响应进行分析。图 4为入射角为30°,反射PP波、PSV波、PSH波在方位角0°~360°时的地震AVAZ响应。3种反射波的AVAZ响应均表现出明显的周期性和对称性,且均可以观察到明显的地震方位各向异性特征,即介质中垂直裂缝的存在导致不同方位角处反射振幅产生明显的变化。提取目标层振幅并绘制极坐标图(图 5),可直观地观察到反射振幅的特征;对三者的方位振幅分布拟合成椭圆,其中PP波和PSV波的长轴方向与裂缝方向一致,PSH波的长轴方向与裂缝方向垂直。
|
| 图 4 入射角为30°时PP波(a)、PSV波(b)、PSH波(c)地震AVAZ响应 Figure 4 Seismic AVAZ responses of PP wave(a), PSV wave(b) and PSH wave(c) at incident angle of 30° |
|
|
|
| 图 5 入射角为30°时PP波(a)、PSV波(b)、PSH波(c)方位振幅分布 Figure 5 Azimuth versus amplitude in polar coordinate of PP wave(a), PSV wave(b) and PSH wave(c) at an incident angle of 30° |
|
|
将各向异性反射率法应用于理论模型,得到的计算结果符合其构造和弹性特征,证明了该方法的有效性以及对于正交各向异性介质的适用性,同时也能够较好地观察到相应的裂缝特征。
3.2 罗家地区L井测井数据应用 3.2.1 储层VTI各向异性根据地层特性给定初始各向异性参数,应用各向异性Backus平均理论粗化测井数据,得到等效VTI各向异性介质,并求取尺度粗化后的各向异性参数。
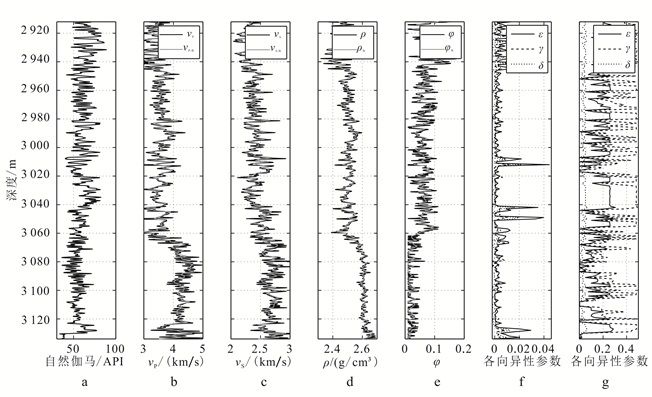
图 6为L井测井曲线,原始测井曲线采样间隔为0.1 m,应用各向异性Backus平均理论计算后曲线的计算长度为1 m[32]。岩石中存在两种各向异性:与层状结构有关的各向异性以及岩石的固有各向异性。当地层中仅存在与层状结构有关的各向异性时,固有各向异性参数为ε=0、γ=0、δ=0。目前对于罗家地区的研究中没有针对岩心的具体描述,因此当地层中同时具有两种各向异性时,针对L井:自然伽马数值大于55 API指示岩性为VTI各向异性的页岩,可引入Sondergeld等[33]研究中给出的页岩固有各向异性参数ε=0.256、γ=0.481、δ=0.051;自然伽马数值小于等于55 API时,固有各向异性参数均为0。图 6f、g分别为两种假设条件下计算得到的VTI等效介质的地震各向异性参数。
|
|
各向异性参数初始值:f. ε=0, γ=0, δ=0;g. ε=0.256, γ=0.481, δ=0.051。 黑色曲线为原始测井曲线,灰色曲线为Backus平均后曲线。 图 6 罗家地区L井及等效介质测井曲线 Figure 6 Well log data from Well L in Luojia area and equivalent medium |
|
|
各向异性Backus平均理论在两种假设条件下计算得到的等效介质弹性参数曲线没有明显变化,这与Backus提出的理论相符,即各向同性介质与VTI各向异性介质平均后得到的等效介质均为VTI各向异性,同时验证了本文应用Backus平均理论计算的正确性。对比两种假设的各向异性参数可以看出:ε和δ与纵波速度成相反的变化趋势;而且地层中同时存在两种各向异性时,各向异性参数数值变化更明显,对各采样点特征的反映更敏感,有助于精确描述地下结构特征。
3.2.2 储层正交各向异性利用Schoenberg线性滑动理论将垂直裂缝引入VTI各向异性等效介质,构建正交各向异性介质模型,计算中e=0.1。
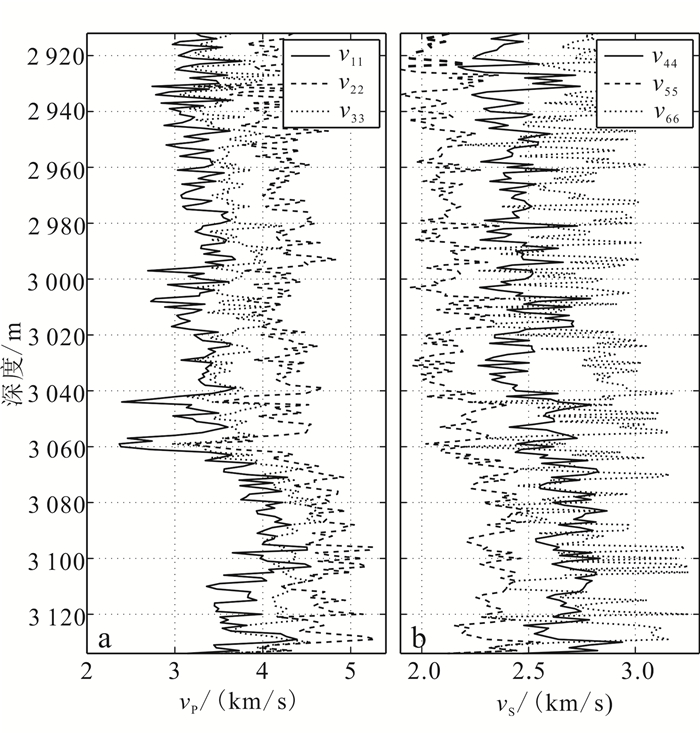
图 7a正交各向异性介质模型中沿x、y、z方向的纵波速度分别为v11、v22和v33。v33 < v22说明在等效介质模型中存在水平层理或水平裂缝,引起纵波在沿z方向传播的过程中速度减小;v11 < v33则由垂直裂缝的存在所引起,若存在水平裂缝,v11 < v33也说明了垂直裂缝密度大于水平裂缝密度。图 7b模型中沿x、y、z方向的横波速度分别为v44、v55和v66,三者数值上的关系为v55 < v44 < v66。v55的数值小于v44和v66,原因是v55同时受到VTI各向异性和垂直裂缝的影响,但是v44仅受到水平裂缝的影响,v66仅受到垂直裂缝的影响。
|
| 图 7 罗家地区L井方位各向异性模型中各方向速度 Figure 7 Velocities in different directions of the orthorhombic model of Well L in Luojia area |
|
|
由以上分析可知,在罗家地区L井测井数据构建的正交各向异性介质模型中存在沿z方向的垂直裂缝,且VTI各向异性介质中发育水平层理和沿y方向的水平裂缝,计算得到的纵横波各方向速度大小符合正交各向异性特征。
3.2.3 全波场地震响应模拟及分析对理论模型的计算验证了应用反射率法模拟正交各向异性介质地震响应的可行性。当入射角过大时会发生相位反转;为了保证计算效果和分析的准确性,在接下来的地震AVAZ响应计算中选取入射角范围为0°~40°。
前文对罗家地区L井建立岩石物理模型,并计算各方向上的纵、横波速度,对储层中的构造进行了初步分析。现综合测井、岩石物理和地震资料进行层位标定:首先对测井数据及各方向速度进行深-时转换,然后应用各向异性反射率法模拟地震AVAZ响应,并将合成地震记录上的标志层与测井曲线以及速度曲线进行标定。由于本文的声波和密度测井数据不是全井段数据,模拟的合成地震记录在地震剖面上存在浮动现象,因此需要通过比对测井数据和合成地震记录中的标志性层位,来建立正确的深-时对应关系。
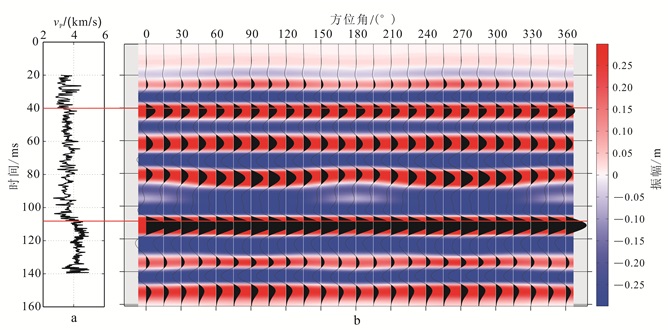
图 8为对L井进行的井震标定[34-36]示意图。可以看出:应用反射率法计算得到的AVAZ响应显示出的振幅变化与速度突变处一致;证明了对声波数据建立的深-时转换曲线的准确性,也证明了各向异性反射率法在研究区的适用性。因此,在测井曲线上表现不明显的信息也可以通过地震资料来观测。
|
| a.纵波速度;b.反射PP波全波场AVAZ响应。 图 8 罗家地区L井的井震标定结果 Figure 8 Well-to-seismic calibration of Well L in Luojia area |
|
|
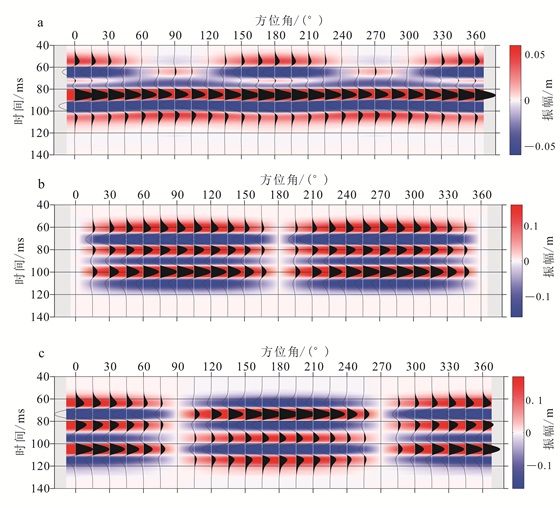
图 9为入射角为30°的反射PP波、PSV波和PSH波的全波场地震AVAZ响应,显示方位角范围为0°~360°。可以看出,固定入射角度时,方位各向异性特征随着方位角的变化有着明显的规律性变化:在PP波和PSV波的AVAZ响应中这种特征存在周期性,180°为一个周期,在一个周期内振幅随方位角的变化以90°为轴两侧具有对称性;PSH波的AVAZ响应则是以180°为轴两侧对称,而且可以观察到振幅随方位角的变化发生了极性反转。另外,在AVAZ响应中可以明确观察到:PP波和PSV波观测方向与垂直裂缝发育方向垂直时(方位角为0°,180°,360°),地震响应中的振幅值应较小,当观测方向与垂直裂缝发育方向平行时(方位角为90°,270°)振幅达到峰值;PSH波与之相反。同时,深层位置的方位各向异性特征比浅层更明显。

|
| 入射角为30°。 图 9 罗家地区L井反射PP波(a)、PSV波(b)、PSH波(c)地震AVAZ响应 Figure 9 Seismic AVAZ responses of PP wav(a)e, PSV wave(b) and PSH wave(c) of Well L in Luojia area |
|
|
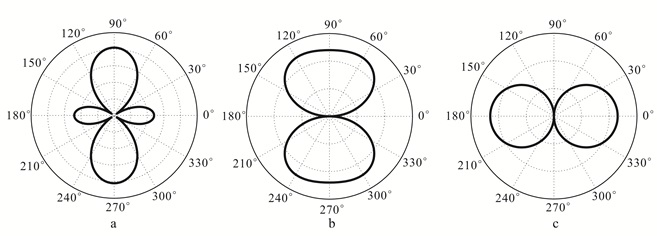
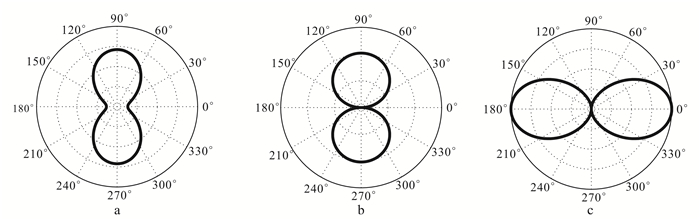
将速度突变界面处的3种反射波振幅提取出来,观测其随方位角的变化规律,结果如图 10所示。PP波的反射振幅随着方位角变化的分布可拟合成椭圆形,长轴方向与模型中的垂直裂缝发育方向一致;PSV波的反射振幅随方位角变化成数字“8”分布,垂向对称轴方向与垂直裂缝方向一致;PSH波的反射振幅成“∞”形状分布,水平向对称轴与垂直裂缝方向垂直。在方位振幅分布上,可以看出3种反射波的图像在垂直和水平两个方向上均存在对称性,且反射PSV波和PSH波均存在零值点;但是结合全波场地震AVAZ响应可以发现,反射PSH波的反射振幅产生了极性反转。因此,结合地震AVAZ响应和反射波方位振幅分布,可以清晰地观察到方位各向异性特征,并以此判断页岩储层中垂直裂缝的走向。
|
| 图 10 罗家地区L井反射PP波(a)、PSV波(b)、PSH波(c)方位振幅分布 Figure 10 Azimuth versus amplitude in polar coordinate of PP wave(a), PSV wave(b), PSH wave(c) of Well L in Luojia area |
|
|
针对罗家地区页岩储层构造特征,本文提出并实现了基于测井数据建立地震尺度非均匀的正交各向异性速度模型,并利用各向异性反射率法对储层反射PP波、PSV波和PSH波的地震AVAZ响应进行模拟,主要结论如下:
1) 通过在地震尺度非均匀各向异性条件下构建正交各向异性等效介质模型,模拟了水平层理发育垂直裂缝的储层地质特征和弹性特性。
2) 针对罗家地区L井建立正交各向异性模型,并应用各向异性反射率法,计算其反射PP波、PSV波和PSH波地震AVAZ响应,清晰展示了由于裂缝的发育,地震响应的方位各向异性特征及其变化规律。相比于浅层位置,深层的方位各向异性特征更明显。
3) 提取标志层反射PP波、PSV波和PSH波反射振幅绘制全波场方位振幅分布图,同时结合地震AVAZ响应,可以观察到裂缝相对于观测方向的发育角度,PP波和PSV波的分布图中,拟合成椭圆的长轴方向与裂缝方向一致,PSH波的分布图拟合成椭圆的长轴方向则与裂缝方向相垂直。因此,全波场地震响应可作为判断裂缝方向的指示工具,为页岩储层裂缝识别和预测提供依据。
| [1] |
慈兴华, 刘宗林, 王志战. 罗家地区泥质岩裂缝性储集层综合研究[J].
录井工程, 2006, 17(1): 71-74.
Ci Xinghua, Liu Zonglin, Wang Zhizhan. Composite Study on Fractured Reservoir of Argillaceous Rock in Luojia Area[J]. Mud Logging Engineering, 2006, 17(1): 71-74. |
| [2] |
王永诗, 李政, 巩建强, 等. 济阳坳陷页岩油气评价方法:以沾化凹陷罗家地区为例[J].
石油学报, 2013, 34(1): 83-91.
Wang Yongshi, Li Zheng, Gong Jianqiang, et al. Discussion on an Evaluation Method of Shale Oil and Gas in Jiyang Depression:A Case Study on Luojia Area in Zhanhua Sag[J]. Acta Petrolei Sinica, 2013, 34(1): 83-91. DOI:10.7623/syxb201301009 |
| [3] |
王敏, 朱家俊, 余光华, 等. 罗家地区泥页岩岩相特征及测井分析技术[J].
测井技术, 2013, 37(4): 426-431.
Wang Min, Zhu Jiajun, Yu Guanghua, et al. The Shale Lithofacies Characteristics and Logging Analysis Techniques in Luojia Area[J]. Well Logging Technology, 2013, 37(4): 426-431. |
| [4] |
袁静. 沾化凹陷罗家地区沙四段顶部至沙三段泥质岩裂缝特征及其影响因素[J].
中国石油大学学报(自然科学版), 2003, 27(4): 20-23.
Yuan Jing. Characteristics of Fractures in Argillaceous Rocks of Luojia Area in Zhanhua Sag[J]. Journal of the University of Petroleum, China, 2003, 27(4): 20-23. |
| [5] |
刘惠民, 张守鹏, 王朴, 等. 沾化凹陷罗家地区沙三段下亚段页岩岩石学特征[J].
油气地质与采收率, 2012, 19(6): 11-15.
Liu Huimin, Zhang Shoupeng, Wang Pu, et al. Lithologic Characteristics of Lower Es3 Shale in Luojia Area, Zhanhua Sag[J]. Petroleum Geology and Recovery Efficiency, 2012, 19(6): 11-15. |
| [6] |
李超, 朱筱敏, 朱世发, 等. 沾化凹陷罗家地区沙三下段泥页岩储层特征[J].
沉积学报, 2015, 33(4): 795-808.
Li Chao, Zhu Xiaomin, Zhu Shifa, et al. Shale Reservoir Characteristics of the Lower 3th Member of Shahejie Formation, Luojia Area, Zhanhua Sag[J]. Acta Sedimentologica Sinica, 2015, 33(4): 795-808. |
| [7] |
关丽. 偶极子声波测井在罗家地区沙三段泥页岩储层评价中的应用[J].
测井技术, 2012, 36(5): 495-498.
Guan Li. Application of Dipole Acoustic Logging to Shale Reservoir Evaluation of Luojia Area[J]. Well Logging Technology, 2012, 36(5): 495-498. |
| [8] |
赵铭海, 傅爱兵, 关丽, 等. 罗家地区页岩油气测井评价方法[J].
油气地质与采收率, 2012, 19(6): 20-24.
Zhao Minghai, Fu Aibing, Guan Li, et al. Logging Evaluation Method of Shale Oil and Gas Reservoir in Luojia Area[J]. Petroleum Geology and Recovery Efficiency, 2012, 19(6): 20-24. |
| [9] |
尹克敏, 李勇, 慈兴华, 等. 罗家地区沙三段泥质岩裂缝特征研究[J].
断块油气田, 2002, 9(5): 24-27.
Yin Kemin, Li Yong, Ci Xinghua, et al. Study on Characters of Muddy Fractural Reservoirs in Luojia Area[J]. Fault-Block Oil & Gas Field, 2002, 9(5): 24-27. |
| [10] |
丁文龙, 许长春, 久凯, 等. 泥页岩裂缝研究进展[J].
地球科学进展, 2011, 26(2): 135-144.
Ding Wenlong, Xu Changchun, Jiu Kai, et al. The Research Progress of Shale Fractures[J]. Advances in Earth Science, 2011, 26(2): 135-144. |
| [11] | Backus G E. Long-Wave Elastic Anisotropy by Horizontal Layering[J]. Journal of Geophysical Research, 1962, 67(11): 4427-4440. DOI:10.1029/JZ067i011p04427 |
| [12] | Schoenberg M, Muir F. A Calculus for Finely Layered Anisotropic Media[J]. Geophysics, 1989, 54(54): 581-589. |
| [13] | Kumar D. Applying Backus Averaging for Deriving Seismic Anisotropy of a Long-Wavelength Equivalent Medium from Well-Log Data[J]. Journal of Geophysics and Engineering, 2013, 10: 1-15. |
| [14] | Zoeppritz K, Erdbebenwellen Ⅷ B. On the Ref-lection and Propagation of Seismic Wave[J]. Gottinger Nachrichten, 1919, 1: 66-84. |
| [15] | Banik N C. An Effective Anisotropy Parameter in Transversely Isotropic Media[J]. Geophysics, 1987, 52(52): 1654-1664. |
| [16] | Thomsen L. WeakElastic Anisotropy[J]. Geophy-sics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [17] | Rüger A. P-Wave Reflection Coefficients for Tran-sversely Isotropic Models with Vertical and Horizontal Axis of Symmetry[J]. Geophysics, 1997, 62(3): 713-722. DOI:10.1190/1.1444181 |
| [18] | Sayers C M, Rickett J E. Azimuthal Variation in AVO Response for Fractured Gas Sands[J]. Geophysical Prospecting, 1997, 45(1): 165-182. DOI:10.1046/j.1365-2478.1997.3180238.x |
| [19] | Schoenberg M A, Dean S, Sayers C M. Azimuth-Dependent Tuning of Seismic Waves Reflected from Fractured Reservoirs[J]. Geophysics, 1999, 64(4): 1160-1171. DOI:10.1190/1.1444623 |
| [20] | Schoenberg M, Protazio J. "Zoeppritz" Rationalized, and Generalized to Anisotropic Media[J]. Journal of Seismic Exploration, 1992, 1(2): 125-144. |
| [21] | Fuchs K, Müller G. Computation of Synthetic Seis-mograms with the Reflectivity Method and Comparison with Observations[J]. Geophysical Journal International, 1971, 23(4): 417-433. DOI:10.1111/j.1365-246X.1971.tb01834.x |
| [22] | Sheriff R E. Seismic Wave Propagation in Stratified Media (B L N Kennett)[M]. Cambridge: Cambridge University Press, 1983. |
| [23] | Booth D C, Crampin S. The Anisotropic Reflectivity Technique:Theory[J]. Geophysical Journal International, 1983, 72(3): 755-766. DOI:10.1111/j.1365-246X.1983.tb02831.x |
| [24] | Fryer G J, Frazer L N. Seismic Waves in Stratified Anisotropic Media:Ⅱ:Elastodynamic Eigensolutions for Some Anisotropic Systems[J]. Geophysical Journal International, 1987, 91(1): 73-101. DOI:10.1111/gji.1987.91.issue-1 |
| [25] | Mallick S, Frazer L N. Computation of Synthetic Seismograms for Stratified Azimuthally Anisotropic Media[J]. Journal of Geophysical Research, 1990, 95(b6): 8513-8526. DOI:10.1029/JB095iB06p08513 |
| [26] | Schoenberg M, Helbig K. Orthorhombic Media:Modeling Elastic Wave Behavior in a Vertically Fractured Earth[J]. Geophysics, 1997, 62(6): 3475-3484. |
| [27] |
李全厚, 裴警博. FMI成像测井解释方法及应用[J].
哈尔滨商业大学学报(自然科学版), 2014, 30(6): 715-719.
Li Quanhou, Pei Jingbo. Interpretation Method and Application of FMI Imaging Logging[J]. Journal of Harbin University of Commerce (Natural Sciences Edition), 2014, 30(6): 715-719. |
| [28] | Woodhouse J H. Surface Waves in a Laterally Va-rying Layered Structure[J]. Geophysical Journal International, 1974, 37(3): 461-490. DOI:10.1111/j.1365-246X.1974.tb04098.x |
| [29] | Gilbert F, Backus G E. Propagator Matrices in Elastic Wave and Vibration Problems[J]. Studia Geophysica et Geodaetica, 1966, 10(3): 271. |
| [30] | Fryer G J, Neil F L. Seismic Waves in Stratified Anisotropic Media[J]. Geophysical Journal of the Royal Astronomical Society, 1987, 78(3): 691-710. |
| [31] | Mallick S, Frazer L N. Rapid Computation of Multioffset Vertical Seismic Profile Synthetic Seismograms for Layered Media[J]. Geophysics, 1988, 53(4): 479-491. DOI:10.1190/1.1442479 |
| [32] | Fei T W. Layer-Induced Seismic Anisotropy from Full-Wave Sonic Logs:Theory, Application, and Validation[J]. Geophysics, 2006, 71(6): D183-D190. DOI:10.1190/1.2356997 |
| [33] | Sondergeld C H, Rai C S. Elastic Anisotropy of Shales[J]. Leading Edge, 2011, 30(3): 324-331. DOI:10.1190/1.3567264 |
| [34] |
张永华, 陈萍, 赵雨晴, 等. 基于合成记录的综合层位标定技术[J].
石油地球物理勘探, 2004, 39(1): 92-96.
Zhang Yonghua, Chen Ping, Zhao Yuqing, et al. Integrative Layer-Labeling Technique Based on Synthetic Seismogram[J]. Oil Geophysical Prospecting, 2004, 39(1): 92-96. |
| [35] |
吴萍, 杨长春, 王真理, 等. HTI介质中的反射纵波方位属性[J].
地球物理学进展, 2009, 24(3): 944-950.
Wu Ping, Yang Changchun, Wang Zhenli, et al. Reflection P-Wave Azimuthal Attribute in HTI Medium[J]. Progress in Geophysics, 2009, 24(3): 944-950. |
| [36] |
逄硕, 刘财, 郭智奇, 等. 基于岩石物理模型的页岩孔隙结构反演及横波速度预测[J].
吉林大学学报(地球科学版), 2017, 47(2): 606-615.
Pang Shuo, Cai Lai, Guo Zhiqi, et al. Estimation of Pore-Shape and Shear Wave Velocity Based on Rock-Physics Modelling in Shale[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(2): 606-615. |



