0 引言
三峡工程作为人类重大工程活动对库区地质环境影响巨大,滑坡作为典型的地质灾害在库区屡屡发生,对当地居民生命财产安全和三峡大坝正常运营构成了严重危害。因此,对三峡库区范围进行滑坡灾害的易发性评价意义重大。
随着遥感、地理信息系统和计算机技术的发展,对于滑坡的易发性评价,国内外学者已经开展了多方面的研究。例如:Carrara[1]利用回归分析对意大利山区滑坡进行易发性评价;Lee[2]基于GIS技术通过逻辑回归模型进行滑坡易发性预测;Ballabio等[3]采用支持向量机模型对意大利北部区域进行了滑坡易发性制图;晏同珍等[4]、殷坤龙[5]多次对三峡库区进行滑坡灾害空间预测;牛瑞卿等[6]利用粗糙集-支持向量机模型实现了三峡库区秭归到巴东段滑坡易发性分区;彭令等[7]、武雪玲等[8]分别在多源数据支持下得到了三峡库区滑坡稳定性分区图。虽然上述研究已经使滑坡空间预测达到了一定的精度,但其中选取的湿度指数因子都只是间接地反应了岩土体含水量,再通过岩土体含水量间接反应地下水信息,而缺少因子来直接表示地表水文状况。
随着微波遥感技术的持续发展,各种适用模型不断改进,大面积反演岩土体含水量已经成为了可能。Paloscia等[9]研究表明,基于神经网络算法利用Sentinel-1影像反演岩土体含水量(soil moisture content,CSM)是可行的;何连等[10]利用多时相Sentinel-1数据实现了农田地表岩土体水分的反演;Oh等[11]根据不同极化方式下粗糙度和介电常数与后向散射系数的相关关系提出了反演岩土体含水量的经验模型;Fung等[12]提出积分方程模型(integrated equation model,IEM),该模型基于辐射传输方程建立地表散射模型;Fung等[13]对IEM进行了改进,得到一种高级积分方程模型(advanced integrated equation model,AIEM);Ulaby等[14]提出了基于微波辐射传输方程一阶解的微波散射模型(michigan microwave canopy scattering model,MIMICSM),主要针对植被覆盖的粗糙地面,是目前应用最多的植被覆盖地区散射模型,但其较为复杂;Attema等[15]提出的水-云模型将植被看作各项散射均质体,模型简单实用。
Hassaballa等[16]分别利用RADARSAT-1雷达数据和Landsat-7 ETM+光学数据反演吉隆坡Bukit Antarabangs滑坡地区地表岩土体含水量,研究其与该地区历史性滑坡的空间相关性,发现利用雷达数据反演得到的含水量与滑坡空间相关性的受试者工作特征曲线下的面积(area under curve,AUC)为0.7且高于光学数据,证明地表岩土体含水量高的地区更易发生滑坡且雷达数据相对光学数据能更好地提取岩土体含水量;Brocca等[17]引入散射计(ASCAT)数据衍生得到的岩土体含水量作为水文因子来预测意大利中部地区Torgiovannetto滑坡的张力裂缝,结果表明其相关系数高于采用降雨量作为水文因子的预测结果,也就意味着岩土体含水量与滑坡的发生具有较强的相关性。
本文在前人研究的基础上,选取三峡库区秭归段作为研究区,利用Sentinel-1雷达数据通过水-云模型去除植被影响得到裸露地表后向散射系数,采取同时相同范围不同极化方式的Sentinel-1雷达数据获取地表粗糙度参数,再利用前人在AIEM的基础上建立的后向散射模型反演得到岩土体含水量;以此作为反映地表水及地下水信息的因子替代其他湿度指数,以实现研究区滑坡易发性评价。
1 岩土体含水量反演和逻辑回归 1.1 岩土体含水量反演 1.1.1 水-云模型水-云模型(water-cloud model)由Attma等[15]于1978年提出,主要为了简化植被覆盖区的后向散射机制,提高模型适用性。该模型将植被层看作一个各项均质散射体,忽略了植被层及地表之间的相互多次散射,将植被覆盖地区总的后向散射简单描述为两部分:由植被层直接反射回的体散射项;经植被层二次衰减后地表的后向散射项。模型表述如下:
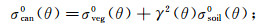 (1)
(1)  (2)
(2)  (3)
(3) 其中:σcan0(θ)为总的雷达后向散射系数;σveg0(θ)为植被层的后向散射系数;σsoil0(θ)为地表后向散射系数;γ2(θ)为雷达波穿透植被层的二次衰减因子;Cveg为植被含水量;θ为雷达波入射角;A、B分别为与植被类型相关的参数。
1.1.2 岩土体含水量反演模型决定裸露地表后向散射系数的参数主要是CSM和地表粗糙度,而地表粗糙度通常由均方根高度(s)在垂直方向相关长度(l)在水平方向上的组合表示。为了简化模型参数,Zribi等[18]提出利用地表粗糙度参数Zs来表示粗糙度,Zs=s2/l。
李震等[19]通过高级积分方程模型的模拟数据,分别建立了同极化雷达后向散射模型和双极化雷达数据粗糙度计算模型,然后将两种模型结合即可求得CSM:
 (4)
(4) 其中:σVH0,σVV0分别为去除植被等影响后的交叉极化(VH极化)、同极化(VV极化)下的雷达后向散射系数;AV(θ),BV(θ),AVV(θ),BVV(θ)和CVV(θ)是与雷达入射角相关的系数[20]。
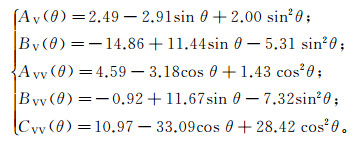 (5)
(5) 逻辑回归模型(logistic regression model)是一种常见的机器学习模型,因其便捷高效,得以普遍应用。因为滑坡只有发生或不发生两种情况(一般1代表发生,0代表未发生),本质上它是一个二分类问题,所以二元逻辑回归模型可以完美地解决滑坡易发性评价中的二分类问题[21]。
我们假设滑坡发生的概率为P,不发生的概率则为1-P。以P作为因变量,xi为自变量,建立回归方程:
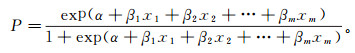 (6)
(6) 式中:α为常数;βm为滑坡各影响因子的逻辑回归系数;xm即代表滑坡各影响因子的相对权重;m为影响因子数目。
2 研究区概况及数据源 2.1 研究区概况研究区位于长江三峡库区秭归县境内,地理坐标为110°30′00″E—110°51′00″E,30°55′00″N—31°04′00″N,面积约为293 km2,其中水系面积约41 km2。研究区位于湖北省西部、三峡库区库首位置(图 1),地势西南高东北低,海拔80~1 500 m,沿江两岸高山林立,为峡谷地貌;气候属亚热带大陆季风气候,雨量充沛。研究区内滑坡灾害频发。

|
| 图 1 研究区位置示意图 Figure 1 Location of the study area |
|
|
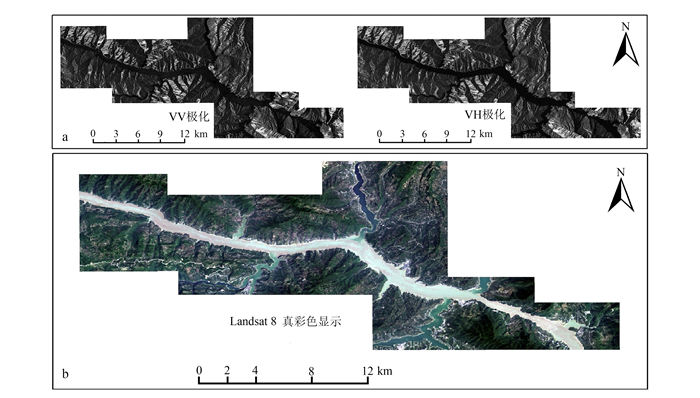
本文主要采用的数据源有:1)图 2a为Sentinel-1A IW(interferometric wide swath)模式下Level-1地距影像(ground range detected,GRD)数据,编号为S1A_IW_GRDH_1SDV_20150826T103524_20150826T103557_007433_00A3CA_0028,用于提取地表岩土体含水量;2)图 2b为Landsat-8 OLI卫星影像一景,编号为LC81250392015216LGN00,用来提取地表覆被信息;3)1:5万比例尺地形图,用于提取地形、地貌等信息;4)1:5万及1:20万比例尺地质图,用于提取地层岩性、构造等信息;5)其他历史滑坡资料和野外调查资料,用于已发生滑坡的解译。
|
| a. Sentinel-1A雷达影像;b.Lansat8影像。 图 2 研究区遥感数据 Figure 2 Remote sensing data of the study area |
|
|
Sentinel-1A作为欧空局(European space agency,ESA)哥白尼全球对地观测计划的首颗卫星于2014年4月发射,主要用于取代Envisat卫星提供全球范围的高分辨率C波段雷达数据。本文选取的数据为Level-1 GRD产品,它经过多视处理并经WGS84椭球投影,只有幅度信息而没有相位信息。Landsat-8由美国国家航空航天局(national aeronautics and space administration, NASA)于2013年2月发射,其携带的OLI(operational land imager)陆地成像仪除了ETM+传感器包含的7个波段外还增加了蓝色波段和短波红外波段。本文所使用的遥感数据参数信息见表 1。
| 影像类型 | 成像时间 | 分辨率/m | 模式 | 入射角/(°) | 频率/GHz | 极化方式 |
| Sentinel-1 | 2015-08-26 | 20×20 | IW GRD | 32.9 | 5.405 | VH+VV |
| Landsat-8 | 2015-08-04 | 30×30 | OLI | |||
| 注:IW GRD.干涉宽幅模式。 | ||||||
对Landsat-8影像处理首先进行辐射定标、大气校正等预处理,然后获取归一化差分水体指数(normalized difference water index,INDW)、归一化植被指数(normalized difference vegetation index, INDV)和土地覆被等信息,主要通过ENVI软件实现;对于Sentinel-1雷达数据的处理主要包括辐射校正、斑点滤波和几何校正,目的是获取植被覆盖地表总的雷达后向散射系数,主要通过ESA开源软件Sentinel application platform实现。
3.2 水-云模型应用植被含水量即为单位面积植被中所含水的质量。作为水-云模型中一个重要的参数,其大面积提取比较困难,通常利用Landsat等陆地影像进行反演。2004年Jackson[22]发现植被含水量Cveg和Gao[23]提出的归一化差分水体指数INDW有很强的联系,即:
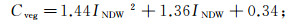 (7)
(7) 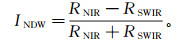 (8)
(8) 其中,RNIR、RSWIR分别代表Landsat-8影像的5、6波段的灰度值。
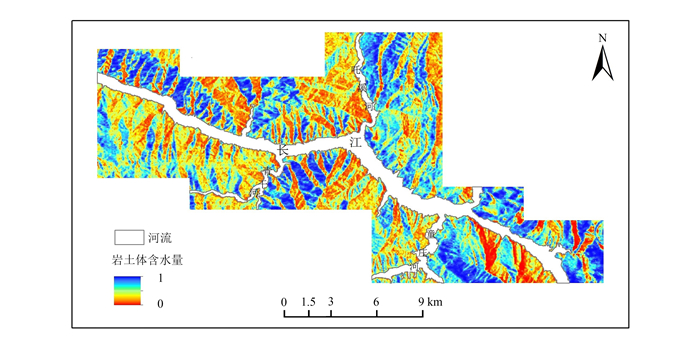
图 3反演得到的含水量只是浅层地表的岩土体含水量,但Uhlemann等[25]通过连续3年的地电监测数据发现滑坡重新激活前浅层岩土体含水量显著提升,同时邓孺孺等[26]的研究也发现深层岩土体含水量与浅层岩土体含水量正相关;两者研究表明浅层地表含水量也显著影响着滑坡的发生且与深层岩土体含水量成正比。虽然深层岩土体含水量对滑坡稳定性具有更重要的意义,但在现有技术手段下反演地表岩土体含水量可能是更现实的选择。
|
| 图 3 岩土体含水量分布图 Figure 3 Map of soil moisture content |
|
|
由于本文数据来源多样,坐标系、投影不尽相同,首先需要对数据统一至相同投影坐标系下。本文选取栅格单元作为评价单元,需将地质、地表覆被等矢量数据转为栅格数据,并将栅格单元大小统一至30 m×30 m。研究发现,土质滑坡较岩质滑坡更易受水的影响[27],所以选取土质滑坡作为研究对象。
4.1 评价因子选取滑坡的发生主要受控制因素和影响因素两大类因素的影响。控制因素指的是研究区的地形、地质构造等因素;影响因素指的是人类工程活动、地表覆被等因素。本文在前人研究的基础上结合研究区的特点选取地质(工程岩组指数(IPT)、断层距离指数(IDF)、斜坡结构指数(ISA))、地形地貌(数字高程(D)、地形粗糙指数(ITR)、地形表面纹理(ITST)、坡度(i))、地表覆被(归一化植被指数(INDV)、土地利用指数(ILU))和水文(水系距离指数(IDR)、地形湿度指数(ITW)、岩土体含水量(CSM))四大类共12个评价因子。为了确保各因子间的相对独立性,利用Pearson积差相关系数法对因子间相关性进行评价(表 2),发现相关系数的绝对值均小于0.75,可以作为因子评价滑坡易发性。
| 相关性 | D | INDV | ITR | ITST | IDF | i | IDR | IPT | ILU | ISA |
| D | 100 | |||||||||
| INDV | -0.46 | 100 | ||||||||
| ITR | 0.10 | -0.16 | 100 | |||||||
| ITST | 0.16 | -0.15 | -0.22 | 100 | ||||||
| IDF | -0.06 | 0.02 | 0.03 | -0.01 | 100 | |||||
| i | 0.10 | -0.20 | 0.64 | -0.23 | 0.04 | 100 | ||||
| IDR | 0.72 | -0.34 | -0.09 | 0.30 | -0.04 | -0.10 | 100 | |||
| IPT | -018 | 0.09 | 一0.16 | 0.12 | 0.21 | -0.14 | 0.01 | 100 | ||
| ILU | -0.26 | 0.25 | -0.10 | -0.02 | -0.01 | -0.12 | -0.15 | 0.16 | 100 | |
| ISA | -0.04 | 0.03 | -0.30 | -0.03 | 0.02 | -0.04 | -0.03 | 0.03 | 0.05 | 100 |
| CSM | 0.08 | -0.07 | 0.15 | -0.05 | -0.01 | -0.17 | 0.00 | -0.17 | -0.32 | -0.07 |
| ITW | -0.03 | 0.00 | -0.01 | -0.01 | 0.01 | 0.00 | -0.00 | -0.02 | -0.03 | -0.01 |
因所选的评价因子处于不同类型、范围和数量级下,归一化处理可以提高数据处理效率,改善模型精度,所以对于连续型因子,我们采用极差标准化方法对其归一化;对于离散型因子(包括斜坡结构、土地利用和工程岩组),我们根据已解译出的滑坡栅格单元中各因子不同属性占总滑坡栅格单元的比例作为各属性的值,再采用极差标准化方法对各属性值进行归一化,结果见表 3。
| 离散因子 | 属性 | 栅格数目 | 所占比例 | 归一化值 |
| 斜坡结构 | 逆斜坡 | 989 | 0.145 | 0.334 |
| 伏倾坡 | 1 147 | 0.168 | 0.392 | |
| 顺斜坡 | 1 153 | 0.169 | 0.394 | |
| 飘倾坡 | 82 | 0.012 | 0.000 | |
| 逆向坡 | 661 | 0.096 | 0.211 | |
| 横向坡 | 2 798 | 0.410 | 1000 | |
| 土地利用 | 耕地 | 5 813 | 0.851 | 1000 |
| 林地 | 536 | 0.078 | 0.009 | |
| 建设用地 | 481 | 0.071 | 0.000 | |
| 工程岩组 | 软岩 | 4 006 | 0.587 | 1000 |
| 硬岩 | 2 667 | 0.390 | 0.651 | |
| 软硬相间岩 | 157 | 0.023 | 0.000 |
基于逻辑回归模型的滑坡预测主要思路就是选取合适的训练和测试样本建立模型并验证模型精度,进而将模型应用到整个研究区,得到研究区滑坡易发性分区图。本文分别使用岩土体含水量,以及前人常用的地形湿度指数为地表湿度指数因子进行易发性研究,并对不同湿度指数因子下易发性评价的精度进行分析,验证采用岩土体含水量因子进行评价的可行性。主要步骤如下:
1) 划分栅格单元。本文采用的数据基本上都是以栅格或矢量形式存在的影像数据,同时结合遥感影像的空间分辨率,将所有评价因子重采样为30 m×30 m大小的栅格单元。经统计可得,研究区共划分为280 670个栅格单元,其中历史土质滑坡单元6 830个,未发生滑坡单元273 840个。
2) 选择建模样本。我们从所有的滑坡栅格单元中随机抽取80%(5 464个栅格单元)和相同数量的未滑坡栅格单元作为训练样本,剩下20%(1 366个栅格单元)滑坡栅格单元作为测试样本。
3) 建立逻辑回归模型。分别采用岩土体含水量、地形湿度指数因子并保持其他因子不变建立模型,客观评价岩土体含水量因子的可行性。采用岩土体含水量因子时模型回归方程为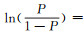
4) 滑坡易发性评价。利用建立的模型对研究区全部栅格单元进行计算,结果输出即为滑坡易发性指数。
5) 结果分析。通过测试样本对滑坡预测结果进行评价,并对比分析采用岩土体含水量、地形湿度指数因子时的预测精度。
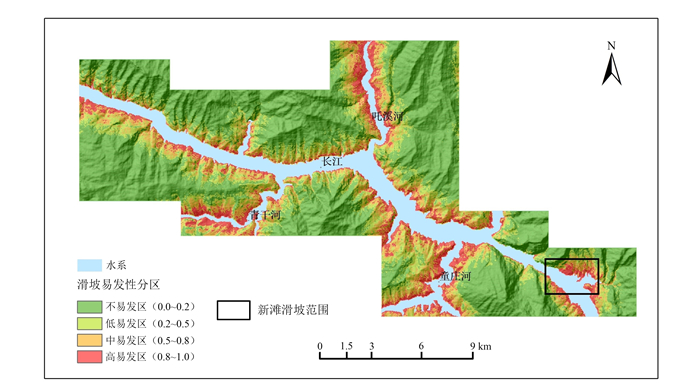
5 结果分析和验证对模型输入整个研究区范围的因子,输出即为介于0.0~1.0之间的滑坡易发性指数,指数越大,滑坡越容易发生,反之滑坡越不容易发生。本文采用自然断点法对滑坡易发性指数进行分区,划分为不易发区(0.0~0.2)、低易发区(0.2~0.5)、中易发区(0.5~0.8)、高易发区(0.8~1.0),得到岩土体含水量因子下滑坡易发性分区图(图 4),并对各分区所占面积比(表 4)进行分析。
|
| ()内为滑坡易发性指数。 图 4 岩土体含水量因子下滑坡易发性分区图 Figure 4 Land slide susceptibility zoning map based on the CSM |
|
|
| 易发性指数 | 易发性分区 | 所占面积比/% | 滑坡所占面积比/% |
| 0.8~1.0 | 高易发区 | 9.7 | 53.6 |
| 0.5~0.8 | 中易发区 | 14.9 | 35.1 |
| 0.2~0.5 | 低易发区 | 16.3 | 9.6 |
| 0.0~0.2 | 不易发区 | 59.1 | 1.7 |
预测结果显示,土质滑坡多发生在河流沿岸,尤其在长江支流童庄河、青干河、吒溪河沿岸易发性指数较高,表明土质滑坡受水的影响较大,基本符合现实滑坡分布状况。
由表 4可知,中高易发区面积仅占研究区总面积的24.6%,而区内滑坡面积却占到了总滑坡面积的88.7%;这也间接表明了我们采用岩土体含水量因子进行滑坡易发性评价是可行有效的。
选择研究区内典型土质滑坡新滩滑坡进行预测结果验证。根据已有历史资料和实际调查资料,新滩滑坡位于屈原镇西北2 km处长江北岸,与链子崖危岩体隔江相望,为古滑坡。最近一次滑动发生于1985年6月12日,滑坡体积约3 000万m3,南北长约2 km,滑动面积约为1.1km2;由于预报及时,新滩镇居民无一伤亡。在滑坡易发性分区图中,该地区被预测为高易发区,如图 5所示。

|
| 图 5 典型滑坡验证 Figure 5 Typical landslide validation |
|
|
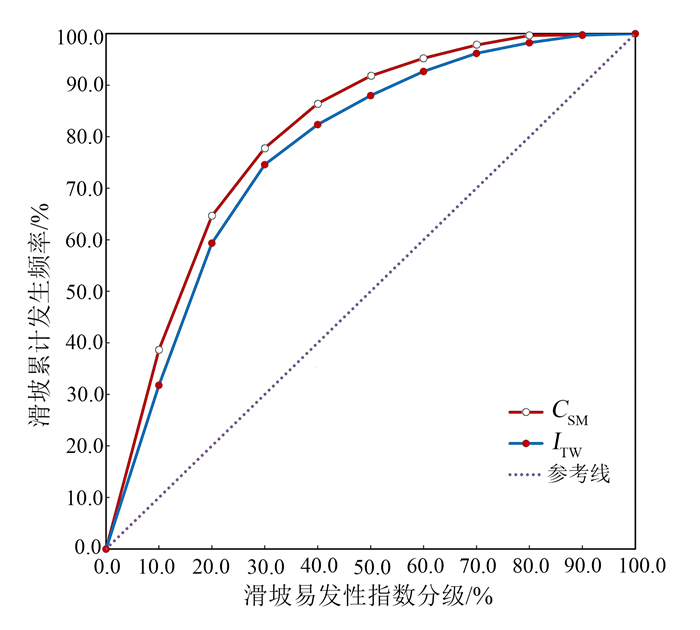
为了检验2个不同湿度指数下滑坡的预测能力并进行对比分析,我们利用测试样本采用Chung等[28]提出的成功率验证法测试2种模型的预测精度(图 6)。图 6中:横轴代表滑坡易发性从大到小分成的100个区间,如横轴10.0%处即表示滑坡易发性指数为90.0%~100.0%的区间;纵轴即为对应易发性区间下实际滑坡累计发生的频率,曲线下面积越大,证明预测效果越好。
|
| 图 6 滑坡累计发生频率与易发性指数曲线 Figure 6 Relation between landslide accumulative frequency and prediction index |
|
|
由图 6可知,对于本文预测的滑坡易发性指数为80.0%~100.0%的区间(横轴20.0%处),即对应易发性分区中的高易发区,采用岩土体含水量、地形湿度指数分别预测了64.6%、59.4%的实际滑坡落在高易发区中,采用岩土体含水量、地形湿度指数因子时曲线下面积即模型预测精度分别为80.2%、77.2%。按照滑坡易发性指数和滑坡累计发生频率将地形湿度指数由数字高程模型中提取的坡度、流域面积计算得到,它主要考虑了地形对地表水的再分配作用来描述岩土体水分的空间分布。但岩土体水分的空间分布还受植被、岩土体特性和人类活动等的干扰,这也决定了地形湿度指数因子只能间接反应岩土体含水量这一重要水文因子对研究区斜坡稳定性的影响。而通过雷达数据可以直接反演出去除植被影响后的裸露地表岩土体含水量,它也与区域范围内地下水的分布状况有很强的联系。同时滑坡预测结果也证明:利用岩土体含水量因子比地形湿度指数因子有着更高的预测准确率,意味着它作为直接反应岩土体含水量的水文因子比其他湿度指数能更好地反应地表及地下水信息,可以作为滑坡易发性评价的重要水文因子。
6 结论与展望1) 通过C波段Sentinel-1雷达数据反演获取岩土体含水量,将其作为一种新引入的水文因子代替地形湿度指数来表征地表及地下水信息。在此基础之上,再充分利用多源空间数据提取其他因子并对数据进行归一化处理,分别建立逻辑回归模型,定量获取滑坡易发性指数,得到研究区易发性分区图。
2) 本文利用雷达数据获取岩土体含水量因子进行滑坡预测的精度要高于传统方法采用的地形湿度指数因子,证明岩土体含水量作为重要的水文因子引入到滑坡预测中是可行的并且精度较好。但由于岩土体含水量的反演受地形及地表覆被的影响较大,现有模型方法普适性较差,大面积反演水文因子仍存在较大困难。
3) 由于条件限制,本文并未测定研究区实地岩土体含水量,如何相对准确的大面积获取岩土体含水量必然是后续研究的重点。随着遥感技术的发展,滑坡空间预测的突破点就在于如何结合利用多源多类型的遥感数据。
| [1] | Carrara A. Multivariate Models for Landslide Hazard Evaluation[J]. Journal of the International Association for Mathematical Geology, 1983, 15(3): 403-426. DOI:10.1007/BF01031290 |
| [2] | Lee S. Application of Logistic Regression Model and Its Validation for Landslide Susceptibility Mapping Using GIS and Remote Sensing Data Journals[J]. International Journal of Remote Sensing, 2005, 26(7): 1477-1491. DOI:10.1080/01431160412331331012 |
| [3] | Ballabio C, Sterlacchini S. Support Vector Machines for Landslide Susceptibility Mapping:The Staffora River Basin Case Study, Italy[J]. Mathematical Geosciences, 2012, 44(1): 47-70. DOI:10.1007/s11004-011-9379-9 |
| [4] |
晏同珍, 杨安顺, 方云.
滑坡学[M]. 武汉: 中国地质大学出版社, 1998.
Yan Tongzhen, Yang Anshun, Fang Yun. Landsile Science[M]. Wuhan: China University of Geosciences Press, 1998. |
| [5] |
殷坤龙.
滑坡灾害预测预报[M]. 武汉: 中国地质大学出版社, 2004.
Yin Kunlong. Prediction and Forecast of Landslide Disaster[M]. Wuhan: China University of Geosciences Press, 2004. |
| [6] |
牛瑞卿, 彭令, 叶润青, 等. 基于粗糙集的支持向量机滑坡易发性评价[J].
吉林大学学报(地球科学版), 2012, 42(2): 430-439.
Niu Ruiqing, Peng Ling, Ye Runqing, et al. Landslide Susceptibility Assess Based on Rough Sets and Support Vector Machine[J]. Journal of Jilin University:Earth Science Edition, 2012, 42(2): 430-439. |
| [7] |
彭令, 徐素宁, 彭军还. 多源遥感数据支持下区域滑坡灾害风险评价[J].
吉林大学学报(地球科学版), 2016, 46(1): 175-186.
Peng Ling, Xu Suning, Peng Junhuan. Regional Landslide Risk Assessment Using Multi-Source Remote Sensing Data[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(1): 175-186. |
| [8] |
武雪玲, 沈少青, 牛瑞卿. GIS支持下应用PSO_SVM模型预测滑坡易发性[J].
武汉大学学报(信息科学版), 2016, 41(5): 665-671.
Wu Xueling, Shen Shaoqing, Niu Ruiqing. Landslide Susceptibility Prediction Using GIS and PSO_SVM[J]. Geomatics and Information Science of Wuhan University, 2016, 41(5): 665-671. |
| [9] | Paloscia S, Pettinato S, Santi E, et al. Soil Moisture Mapping Using Sentinel-1 Images:Algorithm and Preliminary Validation[J]. Remote Sensing of Environment, 2013, 134: 234-248. DOI:10.1016/j.rse.2013.02.027 |
| [10] |
何连, 秦其明, 任华忠, 等. 利用多时相Sentinel-1 SAR数据反演农田地表土壤水分[J].
农业工程学报, 2016, 32(3): 142-148.
He Lian, Qin Qiming, Ren Huazhong, et al. Soil Moisture Retrieval Using Multi-Temporal Sentinel-1 SAR Data in Agricultural Areas[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(3): 142-148. DOI:10.11975/j.issn.1002-6819.2016.03.020 |
| [11] | Oh Y, Sarabandi K, Ulaby F T. An Empirical-Model and an Inversion Technique for Radar Scattering from Bare Soil Surfaces[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(2): 370-381. DOI:10.1109/36.134086 |
| [12] | Fung A K, Li Z Q, Chen K S. Backscattering from a Randomly Rough Dielectric Surface[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(2): 356-369. DOI:10.1109/36.134085 |
| [13] | Fung A K, Chen K S. An Update on the IEM Surface Backscattering Model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 1(2): 75-77. DOI:10.1109/LGRS.2004.826564 |
| [14] | Ulaby F T, Sarabandi K, Mcdonald K, et al. Michi-gan Microwave Canopy Scattering Model[J]. International Journal of Remote Sensing, 1990, 11(7): 1223-1253. DOI:10.1080/01431169008955090 |
| [15] | Attema E P W, Ulaby F T. Vegetation Modeled as a Water Cloud[J]. Radio Science, 1978, 13(2): 357-364. DOI:10.1029/RS013i002p00357 |
| [16] | Hassaballa A A, Althuwaynee O F, Pradhan B. Extraction of Soil Moisture from RADARSAT-1 and Its Role in the Formation of the 6 December 2008 Landslide at Bukit Antarabangsa, Kuala Lumpur[J]. Arabian Journal of Geosciences, 2014, 7(7): 2831-2840. DOI:10.1007/s12517-013-0990-6 |
| [17] | Brocca L, Ponziani F, Moramarco T, et al. Impro-ving Landslide Forecasting Using ASCAT-Derived Soil Moisture Data:A Case Study of the Torgiovannetto Landslide in Central Italy[J]. Remote Sensing, 2012, 4(5): 1232-1244. DOI:10.3390/rs4051232 |
| [18] | Zribi M, Dechambre M. A New Empirical Model to Retrieve Soil Moisture and Roughness from C-band Radar Data[J]. Remote Sensing of Environment, 2003, 84(1): 42-52. DOI:10.1016/S0034-4257(02)00069-X |
| [19] |
李震, 陈权, 任鑫. Envisat-1双极化雷达数据建模及应用[J].
遥感学报, 2006, 10(5): 777-782.
Li Zhen, Chen Quan, Ren Xin. Modeling Envisat Dual Polarized Data and Its Applications[J]. Journal of Remote Sensing, 2006, 10(5): 777-782. |
| [20] |
李震, 廖静娟.
合成孔径雷达地表参数反演模型与方法[M]. 北京: 科学出版社, 2011.
Li Zhen, Liao Jingjuan. Surface Parameter Inversion Model and Method Based on SAR[M]. Beijing: Science Press, 2011. |
| [21] |
文海家, 胡东萍, 王桂林. 汶川县地震滑坡易发性LR与NN评价比较研究[J].
土木工程学报, 2014(增刊1): 17-23.
Wen Haijia, Hu Dongping, Wang Guilin. A Comparative Study on the Susceptibility Mapping of Earthquake Triggered Landslide by Neural Network and Logistic Regression Model, Wenchuan County[J]. China Civil Engineering Journal, 2014(Sup.1): 17-23. |
| [22] | Jackson T. Vegetation Water Content Mapping Using Landsat Data Derived Normalized Difference Water Index for Corn and Soybeans[J]. Remote Sensing of Environment, 2004, 92(4): 475-482. DOI:10.1016/j.rse.2003.10.021 |
| [23] | Gao B. NDWI-A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space[J]. Remote Sensing of Environment, 1996, 58(3): 257-266. DOI:10.1016/S0034-4257(96)00067-3 |
| [24] | Bindlish R, Barros A P. Parameterization of Vege-tation Backscatter in Radar-Based, Soil Moisture Estimation[J]. Remote Sensing of Environment, 2001, 76(1): 130-137. DOI:10.1016/S0034-4257(00)00200-5 |
| [25] | Uhlemann S, Chambers J, Wilkinson P, et al. Four-Dimensional Imaging of Moisture Dynamics During Landslide Reactivation[J]. Journal of Geophysical Research Earth Surface, 2017, 122(1). |
| [26] |
邓孺孺, 陈晓翔, 何执兼. GIS支持下的深层土壤含水量遥感调查方法[J].
中山大学学报(自然科学版), 1997(3): 103-106.
Deng Ruru, Chen Xiaoxiang, He Zhiqian. A GIS Based Remote Sensing Method for Underground Soil Moisture Test[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 1997(3): 103-106. |
| [27] |
彭令. 三峡库区滑坡灾害风险评估研究[D]. 武汉: 中国地质大学, 2013.
Peng Ling. Landslide Risk Assessment in the Three Gorges Reservoir[D]. Wuhan: China University of Geosciences, 2013. |
| [28] | Chung C, Fabbri A G. Probabilistic Prediction Models for Landslide Hazard Mapping[J]. Photogrammetric Engineering and Remote Sensing, 1999, 65(12): 1389-1399. |



