0 引言
逆时偏移理论从提出到现在已经取得了很多的研究成果。其核心概念是利用模拟的震源波场和观测到的检波点波场对地下构造和界面进行成像。与声波逆时偏移相比,弹性波逆时偏移更符合实际情况,能够处理多分量数据,而且转换波的成像结果有更高的分辨率。因此,近些年有很多关于弹性波逆时偏移的研究[1-6]。还有一些研究涉及到横向各向同性(VTI)介质[7-8]。然而,对于弹性波逆时偏移,在源波场和检波点波场中都存在P波和S波。为了减少成像结果中的串扰假象,在逆时偏移之前进行P波和S波分解就变得非常必要。
传统的波场分解方法,比如Helmholtz分解,以及基于散度和旋度算符的波场分解方法,会在分解结果中失去原有的振幅和相位信息。这会导致两个问题:1)不能做到真振幅偏移;2)在转换S波(PS)成像结果中出现极性反转现象。虽然有很多研究可以解决这种极性反转现象[1-3, 5],但是这会增加很多计算量。与这些传统的波场分解方法不同,目前还有3种向量分解方法可以分解P波和S波,并保留向量信息。一种是在频率-波数域中实现的波场分解方法。这种方法可以在各向同性介质中,甚至在倾斜横向各向同性(TTI)介质中,实现P波和S波分解。但是这种方法需要在源波场和检波点波场外推过程中的每个时间点做一次正反傅里叶变换,会大大地增加计算量。另外两种方法分别基于选择吸收和解耦传播。Wang等[9]比较了这两种算法,并认为后一种更有效率。基于解耦传播的波场分解方法有两种实现方式,Xiao等[10]利用P波应力来重建解耦的波动方程,进而实现P波和S波分解。他们还推测这种方法在VTI介质中也是有效的。因此,我们主要讨论这种方法在各向同性介质和VTI介质弹性波逆时偏移中的实用效果。
为了研究波场分解方法对最终成像的影响,我们还需要选择一个合适的成像条件。目前,用于逆时偏移的成像条件主要包括激发振幅(EA)成像条件、互相关(CC)成像条件和震源归一化互相关(SNC)成像条件。激发振幅成像条件不仅不需要存储源波场数据,还具有较高的精度。互相关成像条件和震源归一化互相关成像条件都是比较可靠的成像条件,但是需要存储源波场数据,对内存要求高。因此,从原理上就不需要保存全部源波场数据的激发振幅成像条件更有利于应用到实际中。2013年,Nguyen等[11]在声波逆时偏移中详细论述了该激发振幅成像条件。2015年,Wang等[12]把激发振幅成像条件推广到弹性波逆时偏移(RTM)中,并称其为基于向量的(VB)成像条件。2017年,Zhou等[13]改进了基于向量的成像条件,推导出了基于向量的激发振幅成像(VEA)条件。该成像条件充分考虑了质点振动方向,可以直接求出含有符号的角度依赖的反射系数。
马德堂等[14]在2003年用伪谱法模拟了基于解耦方程的弹性波波场分解。张智等[15]在2013年针对弹性波逆时偏移,提出了稳定的激发振幅成像条件。2016年,李振春等[16]在传统波场分离基础上,对标量势与矢量势分别进行梯度和旋度处理,得到矢量纵波与矢量横波,研究了基于矢量波场分离的弹性波逆时偏移成像。同年,杨绍伟等[17]对弹性波逆时偏移中的子波拉伸现象进行了校正,提高了偏移后纵横波的垂向分辨率。2017年,杨弘宇等[18]基于Poynting矢量研究了地震定向照明分析和成像补偿方法。
本文首先推导基于解耦传播的波场分解方法和基于向量的激发振幅成像条件在各向同性介质和VTI介质中的表达式,然后通过数值模拟实验测试该波场分解方法在各向同性介质和VTI介质中的波场分解效果,最后通过逆时偏移成像结果分析该波场分解方法对最终成像的影响。
1 理论 1.1 弹性波波场传播模拟基于一阶应力速度方程的高阶交错网格有限差分法被广泛用于弹性波正演模拟中。在二维情况下,对于VTI介质,一阶应力速度方程可以表示成:
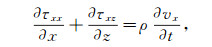 (1)
(1) 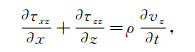 (2)
(2)  (3)
(3) 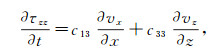 (4)
(4)  (5)
(5) 式中:t表示时间;τxx,τzz和τxz分别代表两个正应力分量和一个剪切应力分量;vx和vz分别代表质点速度的水平和垂直分量;ρ表示介质密度;cij表示介质弹性参数(i, j=1, 3, 4)。如果介质是各向同性的,则c11=c33=λ+2μ,c13=λ,c44=μ,其中λ和μ是拉梅常数。为了兼顾计算效率和计算精度,模拟时我们采用2阶时间差分和12阶空间差分来求解上述方程。同时,我们还采用了基于最小二乘优化的差分系数,完全匹配层(PML)边界和OpenMP并行算法。
1.2 基于解耦传播的波场分解方法对于各向同性介质,基于解耦传播的波场分解方法可以通过构建一个额外的P波应力来实现[10],也可以通过分解应力速度方程来实现[19]。这两种方法在数学上是一致的,而前者的推导更加简便。
对于各向同性介质,P波应力(τP)是一个散射场,计算公式为
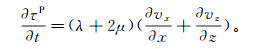 (6)
(6) 然后,可以利用有限差分法由τP得到P波质点速度分量vxP和vzP,即
 (7)
(7) 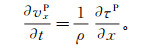 (8)
(8) 最后,从全部波场中减去P波分量就可以得到S波分量,即
 (9)
(9)  (10)
(10) 式中,vzS和vxS分别表示S波质点速度的垂直和水平分量。
对于各向异性介质,P波应力不再是散射场。P波应力的水平和垂直分量可以表示成:
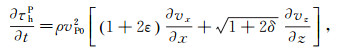 (11)
(11)  (12)
(12) 式中:τhP和τvP分别是P波应力的水平和垂直分量;vP0是模型的P波速度;δ和ε表示介质的各向异性参数(δ与介质的近垂直P波各向异性有关,ε与介质的水平和垂直P波速度差异有关)。相应地,水平和垂直方向上的P波质点速度分量也要由对应的P波应力分量来求解,即
 (13)
(13) 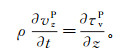 (14)
(14) 然后从全部波场中减去P波分量就可以得到S波分量,即与公式(9)、(10)相同。
分解后的P波和S波分量可以用于计算Poynting矢量、入射角和反射系数。另外,尽管在逆时偏移过程中,速度模型经过了合适的圆滑,为了避免源波场数据(成像时主要利用源波场的P波分量)混入偶然产生的S波分量,不仅要在检波点波场反传时采用波场分解,在源波场正传时也要采用波场分解。特别是含有各向异性介质的模型,在源波场正传过程中肯定会产生S波,这时一定要采用波场分解,得到纯粹的P波分量。
1.3 弹性波逆时偏移成像条件基于向量的激发振幅成像条件是激发振幅成像条件在弹性介质中的推广。因此,与声波介质中的激发振幅成像条件类似,也需要在源波场正传过程中先计算成像时刻,即
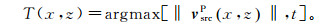 (15)
(15) 式中:T表示每个网格点的成像时刻;‖vsrcP‖表示源波场P波质点速度向量的模。该成像时刻是把每个质点在所有时刻的最大振幅所在的时刻作为成像时刻。
因为逆时偏移中还需要计算入射角,我们还需要计算Poynting矢量。对于VTI介质,P波Poynting矢量可以表示成:
 (16)
(16) 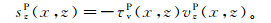 (17)
(17) 式中,sxP和szP分别表示P波Poynting矢量的水平和垂直分量。同样S波的Poynting矢量可以表示成:
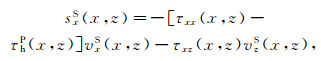 (18)
(18) 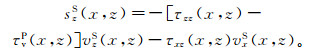 (19)
(19) 式中,sxS和szS分别表示S波Poynting矢量的水平和垂直分量。如果是各向同性介质,则τhP=τvP=τP,将式(16)—(19)简化一下即可。
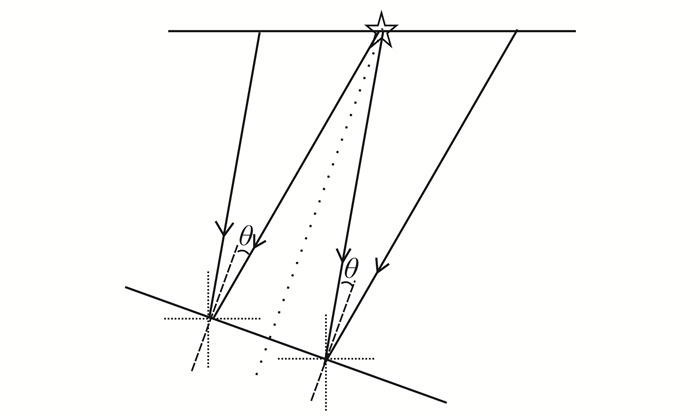
根据几何关系(图 1),入射角可以表示成
 (20)
(20)
|
| 图 1 入射角和Poynting矢量之间的几何关系 Figure 1 Geometry relationship between Poynting vectors and incident angle |
|
|
式中:sz, srcP和sx, srcP分别表示源波场P波Poynting矢量的垂直和水平分量;sz, recP和sx, recP分别表示检波点波场P波Poynting矢量的垂直和水平分量。
根据激发振幅成像条件,反射系数可以用检波点波场除以存储的源波场最大振幅来计算。在弹性介质中,我们用向量的内积来代替向量的模,然后用角度余弦来矫正计算误差,即
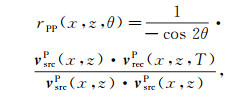 (21)
(21)  (22)
(22) 式中:rPP和rPS分别表示PP波和PS波的角度依赖反射系数;vrecP和vrecS分别表示检波点波场的P波和S波的质点速度向量;φ表示入射P波质点振动方向与反射S波质点振动方向之间的夹角(图 2);θ′是转换S波的反射角(图 2)。夹角φ可以表示成
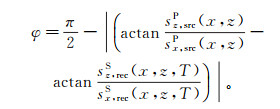 (23)
(23)

|
| 图 2 质点振动方向和角度之间的几何关系 Figure 2 Geometry relationship between particle velocity vectors and angles |
|
|
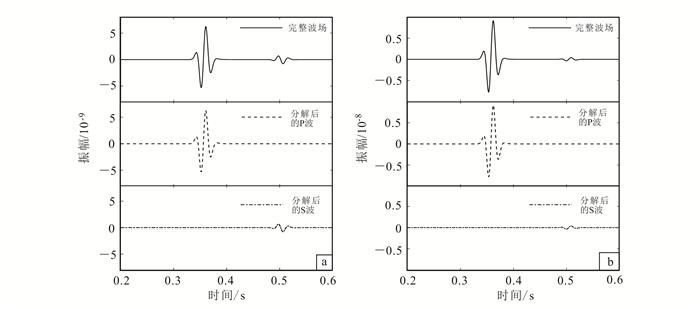
首先测试该波场分解算法在各向同性介质中的P波和S波分离效果。我们设计了一个两层模型,水平方向和垂直方向都是2 km,每层的厚度都是1 km。第一层的P波速度、S波速度和密度分别为2 500 m/s、1 500 m/s和2 000 kg/m3;第二层的P波速度、S波速度和密度分别为2 700 m/s、1 600 m/s和2 100 kg/m3。采用的波场分解方法针对的是各向同性介质,即公式(6)—(10)。图 3是0.4 s时的波场快照,可以明显看出在各向同性介质中,无论是直达波、反射波或透射波,都能分解得很好,并且没有残余。为了更清晰地比较波场分解结果,我们还给出了两个网格点(x=1.5 km, z=0.5 km)和(x=1.5 km, z=1.5 km)处的部分记录,分别如图 4和图 5所示。第一个网格点位于第一层,可以看出,对于直达波、反射波和转换波,P波和S波都分解得非常干净(图 4)。第二个网格点位于第二层,可以看出,对于透射波和转换波,P波和S波也分解得非常干净(图 5)。

|
| a.水平分量;b.分解后的P波水平分量;c.分解后的S波水平分量;d.垂直分量;e.分解后的P波垂直分量;f.分解后的S波垂直分量。 图 3 各向同性介质中的波场快照(T=0.4 s) Figure 3 Snapshots in isotropic media (T=0.4 s) |
|
|

|
| a.水平分量;b.垂直分量。 图 4 各向同性介质中检波点位于x=1.5 km、z=0.5 km处的部分记录 Figure 4 Measurements of the receiver at x=1.5 km and z=0.5 km in isotropic media |
|
|
|
| a.水平分量;b.垂直分量。 图 5 各向同性介质中检波点位于x=1.5 km、z=1.5 km处的部分记录 Figure 5 Measurements of the receiver at x=1.5 km and z=1.5 km in isotropic media |
|
|
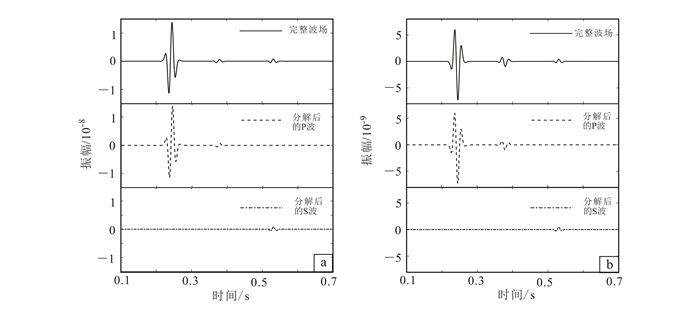
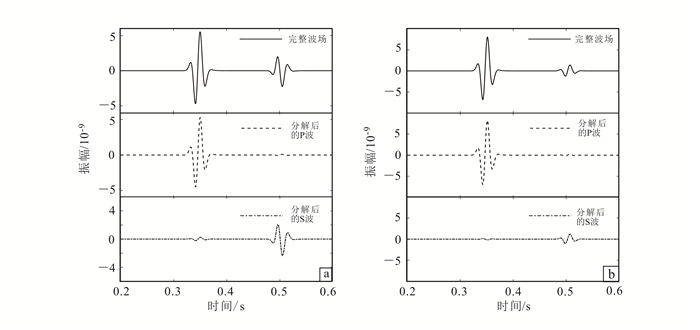
然后我们把第二层介质改为VTI介质,各向异性参数ε和δ分别是0.204和0.175,其他介质参数不变。模型大小和波场快照时间也与上面的各向同性介质测试相同。采用的波场分解方法针对的是VTI介质,即公式(11)—(14),结果如图 6所示。可见:在第一层介质中P波和S波的分解结果依旧很好,说明下层介质的参数不会影响反射波的分解效果;但是第二层介质在P波和S波分解结果中都存在较明显的残余(如图 6中的黑箭头所示),说明解耦传播的波场分解方法在VTI介质中不能将P波和S波完全分开。同样,我们也给出了两个网格点(x=1.5 km, z=0.5 km)和(x=1.5 km, z=1.5 km)处的部分记录(图 7、图 8)。从图 7和图 8可以明显看出,波场在第一层各向同性介质中分解得非常彻底(图 7),在第二层VTI介质中存在分解残余(图 8)。

|
| a.水平分量;b.分解后的P波水平分量;c.分解后的S波水平分量;d.垂直分量;e.分解后的P波垂直分量;f.分解后的S波垂直分量。 图 6 当第二层是VTI介质时的波场快照(T=0.4 s) Figure 6 Snapshots when the second layer is VTI media (T= 0.4 s) |
|
|
|
| a.水平分量;b.垂直分量。 图 7 第二层是VTI介质时检波点位于x=1.5 km、z=0.5 km处的部分记录 Figure 7 Measurements of the receiver at x=1.5 km and z=0.5 km when the second layer is VTI media |
|
|
|
| a.水平分量;b.垂直分量。 图 8 第二层是VTI介质时检波点位于x=1.5 km, z=1.5 km处的部分记录 Figure 8 Measurements of the receiver at x=1.5 km and z=1.5 km when the second layer is VTI media |
|
|
上面的测试结果同时也说明针对VTI介质的波场分解方法可以适用于各向同性介质。然后我们还是针对这个第二层是VTI介质的模型,但是采用针对各向同性介质的波场分解方法,即公式(6)—(10)。波场分解结果如图 9所示。可见在第二层介质中,相比于图 6中的分解结果,无论是x分量还是z分量都存在非常强的波场分解残余(如图 9中黑色箭头所示)。这说明各向同性介质的波场分解方法在VTI介质中的应用效果非常差,不能直接应用于VTI介质的波场分解。同时也间接说明了VTI介质的波场分解方法在VTI介质中的必要性。

|
| a.水平分量;b.分解后的P波水平分量;c.分解后的S波水平分量;d.垂直分量;e.分解后的P波垂直分量;f.分解后的S波垂直分量。 图 9 第二层是VTI介质时采用各向同性波场分解方法的波场快照(T=0.4 s) Figure 9 Snapshots with isotropic wavefield decomposition method when the second layer is VTI media (T=0.4 s) |
|
|
作为对比,我们还得到了Helmholtz分解的结果。图 10是采用Helmholtz分解的波场快照,模型参数和快照时间与之前的测试相同。分解之后的P波和S波分量都失去了原有的振幅和相位信息,只含有一个分量,即从向量波场变成了散射波场。在各向同性介质中分解结果较好,在VTI介质中有很明显的分解残余(黑色箭头所示)。另外,图 10与图 6、图 9中采用的是相同的绘图参数,可见图 10中分解之后的波场振幅也有较大改变,这就不能在最终的成像结果中做到真振幅偏移。

|
| a.水平分量;b.垂直分量;c.分解后的S波分量;d.分解后的P波分量。 图 10 第二层是VTI介质时采用Helmholtz分解的波场快照(T=0.4 s) Figure 10 Snapshots with Helmholtz wavefield decomposition method when the second layer is VTI media (T=0.4 s) |
|
|
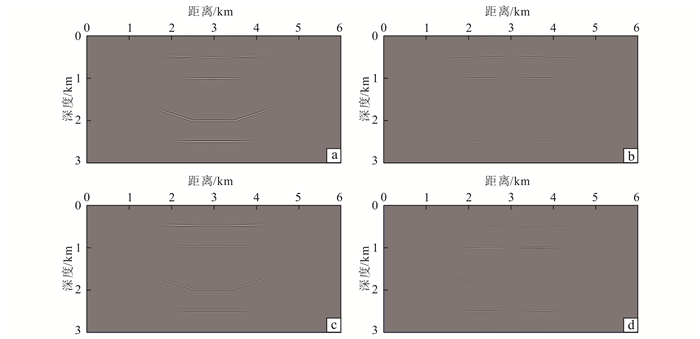
为了测试上述波场分解方法在各向同性介质和VTI介质中的逆时偏移效果,我们测试了以下模型。首先是选择一个洼陷模型(图 11),P波速度如图 11a所示,S波速度与P波速度的关系是vS=vP/1.7, 密度和P波速度的关系是ρ=1.66×vP0.261。水平和垂直方向的模型网格间距都是5 m,震源位于地表x=3 km处,采用的是主频30 Hz的Ricker子波,1 201个检波器均匀分布在地表。首先不考虑介质的各向异性,即各向异性参数为0。我们采用上面介绍的基于解耦传播的波场分解方法和基于向量的激发振幅成像条件得到单炮偏移结果(图 12a、b),PP波和PS波成像结果都比较清晰,没有明显的成像假象,而且PS波成像结果中不存在相位反转现象,多炮偏移结果可以直接叠加。作为对比,我们还采用Helmholtz波场分解方法和激发振幅成像条件得到了单炮偏移结果(图 12c、d),PP波和PS波成像结果也比较清晰,没有明显的成像假象,但是PS波成像结果存在相位反转现象,进而导致多炮叠加结果不连续,不利于最终成像。

|
| 图 11 洼陷模型示意图 Figure 11 Sub-sag model |
|
|
|
| 本文方法:a. PP波成像结果;b. PS波成像结果。Helmholtz分解:c. PP波成像结果;d. PS波成像结果。 图 12 各向同性介质单炮逆时偏移结果 Figure 12 Single shot RTM result for isotropic media |
|
|
然后我们再测试基于解耦传播的波场分解方法和基于向量的激发振幅成像条件在VTI介质中的应用效果。此时,介质的各向异性参数ε和δ如图 11b、c所示,其他参数与之前的各向同性测试相同。其单炮逆时偏移结果如图 13a、b所示,总体上,PP波和PS波成像结果也是比较清晰的,只存在微弱的串扰假象。因此,我们可以认为,基于解耦传播的波场分解方法应用于VTI介质弹性波逆时偏移时也可以得到比较好的成像结果。作为对比,我们还采用Helmholtz波场分解方法和激发振幅成像条件得到了单炮偏移结果(图 13c、d),PP波和PS波成像结果也比较清晰,但是成像假象更多,而且PS波成像结果中依然存在相位反转现象,影响多炮偏移叠加成像效果。

|
| 本文方法:a. PP波成像结果;b. PS波成像结果。Helmholtz分解:c. PP波成像结果;d. PS波成像结果。 图 13 VTI介质的单炮逆时偏移结果 Figure 13 Single shot RTM result for VTI media |
|
|
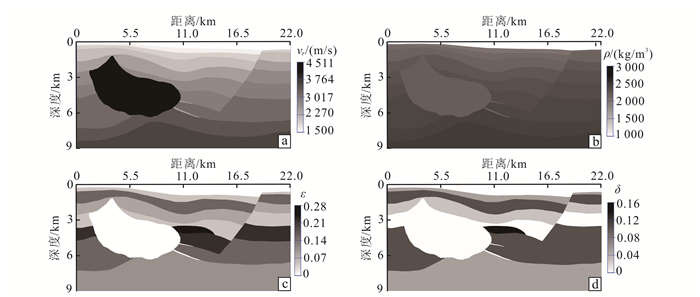
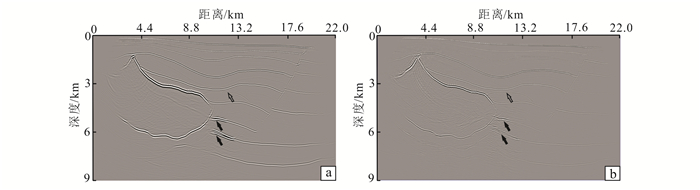
因为采用Helmholtz分解的逆时偏移结果在PS成像中存在相位反转现象,在多炮叠加的时候会造成叠加结果不连续,大大影响成像质量,因此这里只测试了本文方法在复杂Hess VTI模型中的应用效果。模型参数如图 14所示,S波速度设为vP/1.7。模型在水平方向和垂直方向分别有1 808和750个网格点,网格间距12 m。一共141炮分布于地表x=2.4~19.6 km的范围内,炮间距120 m。每炮含有401个检波点,检波点间距是12 m。采用本文的方法,所有141炮的偏移结果叠加后的成像结果如图 15所示。图 15中PP波成像结果和PS波成像结果都较清晰,高速盐丘的边界和断层也成像清晰,特别是图中两个低速夹层也得到了较好的成像(如黑色箭头所示)。另外,相对于PP波成像结果,PS成像结果对各向异性体的成像更好(图中灰色箭头所示),这说明了PS波成像的优势——可以刻画一些PP波成像不能刻画的构造。但是,限于高速岩体的影响,盐丘下面的构造成像不清晰,岩体边缘和两个低速夹层的接触带也没有得到很好的成像,这需要进一步研究。
|
| 图 14 Hess VTI模型 Figure 14 Hess VTI model |
|
|
|
| a. PP波成像结果; b. PS波成像结果。 图 15 Hess VTI模型逆时偏移结果 Figure 15 Migration results of Hess VTI model |
|
|
我们把基于解耦传播的波场分解方法应用到弹性波逆时偏移中,并对比了其在各向同性介质和VTI介质中的应用效果。通过数值模拟可以得到以下结论:
1) 在各向同性介质中,直达波、反射波、转换波和透射波中的P波和S波都能分解得很完全,并保留波场的向量信息。从逆时偏移结果来看,PP波和PS波成像都很清晰,没有串扰假象,也没有相位反转现象。
2) 在VTI介质中,P波和S波的分解结果中都含有对方的残余,说明解耦传播的波场分解方法在VTI介质中的推广不是完全正确的,存在一定的误差。但是该分解残余不会在RTM结果中产生很明显的串扰,说明扩展后的解耦传播波场分解方法是可以应用于VTI介质逆时偏移的。
3) 基于解耦传播的P波和S波波场分离方法是在时间空间域实现的,可以在波场传播过程中直接对P波和S波进行分离。该方法具有应用方便,计算效率高,结果可靠的优点。
4) Hess VTI模型的测试结果表明,本文的方法在复杂介质中也有较好的适应性,成像结果清晰,没有明显的串扰假象。但是,限于高速岩体的影响,盐丘下面的构造成像不清晰,岩体边缘和两个低速夹层的接触带也没有得到很好的成像,这需要进一步研究。
| [1] | Yan J, Sava P. Isotropic Angle-Domain Elastic Reverse-Time Migration[J]. Geophysics, 2008, 73(6): S229-S239. DOI:10.1190/1.2981241 |
| [2] | Yan R, Xie X B. An Angle-Domain Imaging Condition for Elastic Reverse Time Migration and Its Application to Angle Gather Extraction[J]. Geophysics, 2012, 77: S105-S115. |
| [3] | Du Q, Zhang M, Gong X, et al. Polarity-Consistent Excitation Amplitude Imaging Condition for Elastic Reverse Time Migration[J]. Journal of Geophysics & Engineering, 2015, 12(1): 33-44. |
| [4] | Duan Y, Sava P. Scalar Imaging Condition for Elastic Reverse Time Migration[J]. Geophysics, 2015, 80(4): S127-S136. DOI:10.1190/geo2014-0453.1 |
| [5] | Li Z, Ma X, Fu C, et al. Wavefield Separation and Polarity Reversal Correction in Elastic Reverse Time Migration[J]. Journal of Applied Geophysics, 2016, 127: 56-67. DOI:10.1016/j.jappgeo.2016.02.012 |
| [6] | Wang W, McMechan G A, Tang C, et al. Up/Down and P/S Decompositions of Elastic Wavefields Using Complex Seismic Traces with Applications to Calculating Poynting Vectors and Angle-Domain Common-Image Gathers from Reverse Time Migrations[J]. Geophysics, 2016, 81(4): S181-S194. DOI:10.1190/geo2015-0456.1 |
| [7] | Lu R, Yan J, Traynin P, et al. Elastic RTM: Anisotropic Wave-Mode Separation and Converted-Wave Polarization Correction[C]//Expanded Abstracts of the 80th Annual International Meeting. Denver: SEG, 2010: 3171-3175. |
| [8] | Wang C, Cheng J, Arntsen B. Scalar and Vector Imaging Based on Wave Mode Decoupling for Elastic Reverse Time Migration in Isotropic and Transversely Isotropic Media[J]. Geophysics, 2016, 81(5): S383-S398. DOI:10.1190/geo2015-0704.1 |
| [9] | Wang W, McMechan G A, Zhang Q. Comparison of Two Algorithms for Isotropic Elastic P and S Vector Decomposition[J]. Geophysics, 2015, 80(4): T147-T160. DOI:10.1190/geo2014-0563.1 |
| [10] | Xiao X, Leaney W S. Local Vertical Seismic Profiling (VSP) Elastic Reverse-Time Migration and Migration Resolution:Salt-Flank Imaging with Transmitted P-to-S Waves[J]. Geophysics, 2010, 75(2): S35-S49. DOI:10.1190/1.3309460 |
| [11] | Nguyen B D, McMechan G A. Excitation Amplitude Imaging Condition for Prestack Reverse-Time Migration[J]. Geophysics, 2013, 78(1): S37-S46. DOI:10.1190/geo2012-0079.1 |
| [12] | Wang W, McMechan G A. Vector-Based Elastic Reverse Time Migration[J]. Geophysics, 2015, 80(6): S245-S258. DOI:10.1190/geo2014-0620.1 |
| [13] | Zhou J, Wang D. Vector-Based Excitation Amplitude Imaging Condition for Elastic RTM[J]. Journal of Applied Geophysics, 2017, 147: 1-9. DOI:10.1016/j.jappgeo.2017.10.003 |
| [14] |
马德堂, 朱光明. 弹性波波场P波和S波分解的数值模拟[J].
石油地球物理勘探, 2003, 38(5): 482-486.
Ma Detang, Zhu Guangming. Numerical Modeling of P-Wave and S-Wave Separation in Elastic Wavefield[J]. Oil Geophysical Prospecting, 2003, 38(5): 482-486. |
| [15] |
张智, 刘有山, 徐涛, 等. 弹性波逆时偏移中的稳定激发振幅成像条件[J].
地球物理学报, 2013, 56(10): 3523-3533.
Zhang Zhi, Liu Youshan, Xu Tao, et al. A Stable Excitation Amplitude Imaging Condition for Reverse Time Migration in Elastic Wave Equation[J]. Chinese Journal of Geophysics, 2013, 56(10): 3523-3533. DOI:10.6038/cjg20131027 |
| [16] |
李振春, 雍鹏, 黄建平, 等. 基于矢量波场分离弹性波逆时偏移成像[J].
中国石油大学学报(自然科学版), 2016, 40(1): 42-48.
Li Zhenchun, Yong Peng, Huang Jianping, et al. Elastic Wave Reverse Time Migration Based on Vector Wavefield Separation[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016, 40(1): 42-48. |
| [17] |
杨绍伟, 何兵寿, 杨佳佳. 弹性波逆时偏移子波拉伸校正[J].
中国煤炭地质, 2016, 28(2): 61-67.
Yang Shaowei, He Bingshou, Yang Jiajia. Wavelet Stretch Correction in Elastic Wave Reverse Time Migration[J]. Coal Geology of China, 2016, 28(2): 61-67. |
| [18] |
杨弘宇, 刘继承, 段玉波. 基于Poynting矢量的地震照明分析[J].
吉林大学学报(地球科学版), 2017, 47(1): 245-254.
Yang Hongyu, Liu Jicheng, Duan Yubo. Seismic Illumination Analysis Based on the Poynting Vector[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(1): 245-254. |
| [19] | Zhang J, Tian Z, Wang C. P-and S-Wave-Separated Elastic Wave-Equation Numerical Modeling Using 2D Staggered Grid[C]//Expanded Abstracts of the 77th Annual International Meeting. San Antonio: SEG, 2007: 2104-2109. |


