0 引言
近年来,分数阶微积分被广泛应用于黏弹阻尼器、地震分析、反常扩散、信号处理与控制、流体力学、图像处理、软物质研究等多个领域。相对于整数阶导数,分数阶微分算子可以更简洁地描述具有历史依赖性和空间全域相关性的复杂力学和物理过程。随着油气勘测对象的日趋深入与岩石模型的日趋复杂,更多学者考虑到,实际的地下介质并不是完全弹性的,地震波在地下传播过程中会发生能量衰减、相位畸变和频散。引起这3种波场变化的机制为:孔隙及流体、基质黏弹性和各向异性。为了更准确地描述波在实际介质中的传播规律,需要考虑以上3种机制。对于双相孔隙介质:与Biot模型[1]相比,BISQ(Biot-squirt)模型[2]在考虑了Biot流动的同时还考虑了喷射流动,但其特征喷射流动长度为虚数,在时间域处理不太合理,并且物理意义并不十分明确,本文采用不依赖于特征喷射长度的改进的BISQ模型[3]来描述孔隙介质;对于孔隙流体黏滞性:孔隙介质中固、流两相除相对平动外,还存在相对转动,流体的振动速度梯度会产生剪切应变,导致流相中存在剪切应力和附加法相应力[4],应该考虑黏性摩擦力产生的应力偏量;对于固体骨架黏弹性:含分数阶时间导数的常Q(品质因子)模型恰好可以准确地描述固体骨架的黏弹性。
Kjartansson[5]提出的常Q模型认为:衰减因子与频率成线性反比关系,在常规地震频带内,Q值与频率基本无关。基于Kjartansson常Q模型的波传播方程是含有分数阶时间导数的,Carcione[6]采用分数阶导数的Grünwald-Letnikov定义,用全局记忆法进行数值模拟。因为分数阶导数具有全局记忆特性,所以全局记忆法求解波传播方程需要保存每一个时刻的应力-应变值,并且计算某个量某个时刻的时间导数需要之前所有时刻的所有值。即,当前状态与过去所有状态有关,因而所需存储量和计算量均很大,计算效率较低。Podlubny[7]提出“短时记忆法”对分数阶微分算子进行截断,仅考虑当前时刻t以前的有限时间区间[t-L, t],随着短时记忆长度L的选取不同,误差也不同。过去不同时间点对当前时间点的影响是不同的,接近当前时刻时间点对当前时刻的影响较大,而距离当前时刻时间间隔较长的时间点对当前时刻的影响较小。利用这一性质,Brian等[8]于2010年提出“自适应记忆法”。
分数阶导数实际上是整数阶导数的推广,关于分数阶导数的定义,许多数学家从不同角度分别给出了不同定义,其合理性和科学性在实践中已经得到了验证,这个数学分支已在实际问题中得到广泛应用。比较常见的3种分数阶导数定义分别为:Grünwald-Letnikov分数阶导数定义[9]、Riemann-Liouville分数阶导数定义[9]和Caputo分数阶导数定义[9]。Riemann-Liouville分数阶导数定义是Grünwald-Letnikov分数阶导数定义的扩充,Caputo分数阶导数也是对Grünwald-Letnikov分数阶导数定义的另一种改进[10],在阶数为负实数和正整数时三者是等价的。在实际应用中,用哪种形式的定义需依照具体情况而定。
本文基于Kjartansson常Q应力-应变关系,将含有分数阶时间导数的黏弹固体骨架各向异性本构关系与双相介质理论改进BISQ模型有机地结合起来,引入流变学本构关系描述孔隙流体的黏滞性力学行为[11],建立含黏滞流体黏弹双相VTI(横向各向同性)介质中的分数阶波传播方程;并在时间域进行数值模拟,采用全局记忆法、短时记忆法、自适应记忆法对分数阶微分算子进行数值计算,整数阶时间、空间微分算子均采用高阶交错网格有限差分算法;最后对3种方法各自的特点进行归纳总结,并对3种方法进行对比分析。
1 原理由于Grünwald-Letnikov分数阶导数定义是基于Grünwald-Letnikov有限差分近似式导出的,而本文波传播方程中整数阶导数数值模拟采用高阶交错网格有限差分算法进行,故相应地本文中的分数阶时间导数计算采用Grünwald-Letnikov分数阶导数定义。
1.1 Grünwald-Letnikov分数阶导数定义基于Grünwald-Letnikov有限差分近似式,将
 (1)
(1) 称为f(x)的γ阶Grünwald-Letnikov分数阶导数。式中:h为步长;m为节点数;Γ为欧拉伽马函数;α∈R,α≠-N1,N1为除1之外的自然数集。从式(1)可以看出,求得当前时刻分数阶导数需要知道从m=0到m=x/h的所有函数值,这正是分数阶导数的历史依赖性和空间全域相关特性。
1.2 分数阶波传播方程本文采用基于Kjartansson常Q理论的分数阶时间导数黏弹本构关系来描述双相介质固体骨架的黏弹性效应,并引入流变学本构关系表征孔隙流体的黏滞力学行为,根据Yang等[12]提出的包含BISQ机制和固流耦合各向异性效应的孔隙弹性波动理论,给出基于分数阶时间导数常Q黏弹本构关系的含黏滞流体双相VTI介质二维波传播方程。
固体骨架黏弹本构方程为
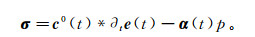 (2)
(2) 式中:σ为总应力张量;c0(t)为干燥固体骨架弛豫函数刚度矩阵;*为卷积运算符;e(t)为固体骨架应变张量;α(t)3×3为有效应力之孔隙弹性系数张量;p为孔隙黏滞流体压力[13],可表示为
 (3)
(3) 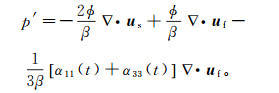 (4)
(4) 式中:η为流体黏滞系数;ϕ为孔隙度;vfi(vfj) (i,j=1, 3)为流相质点在正交方向x, z上的速度分量;xi(xj)(i,j=1, 3)表示x, z轴;us=(us1,us3)T与uf=(uf 1,uf 3)T分别为固相和流相位移矢量;β为双相介质压缩率系数;α11(t)、α33(t)为α(t)3×3的分量;t为时间;下标i, j=(1, 3)分别表示二维平面x, z方向分量,后续公式中i, j意义同此。
几何方程为
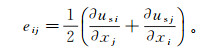 (5)
(5) 式中,eij为固体骨架应变张量分量。
运动方程为
 (6)
(6) 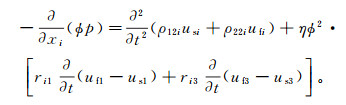 (7)
(7) 式中:σij为总应力张量分量;ρ1=(1-ϕ)ρs;ρ2=ϕρf;ρs为固体密度;ρf为流体密度;ρ22i=ρ2-ρ12i,ρ12i=-ρai,ρai为xi方向的固-流耦合附加质量密度;rij为流体阻抗系数,rij=(kij)-1,kij为渗透率张量k的元素,对于VTI介质,k=diag (k11, k11, k33)。
综合式(3)—(7)即可导出以固相和流相位移usi和ufi为基本未知量的、基于分数阶时间导数常Q黏弹本构关系的含黏滞流体双相VTI介质波传播方程。在二维x-z平面内,这组方程的速度-应力形式是由以下8个方程构成的含卷积运算的偏微分方程组:

 (8)
(8) 其中,

式中:vsx、vsz分别代表固相速度x、z方向分量;vfx和vfz分别代表流相速度x、z方向分量;γP、γS、γ13为分数阶导数阶数,具体意义及CP//、CP⊥、C13∧意义参见文献[14]。
2 稳定性条件和吸收边界条件在进行显式有限差分数值模拟时,需要考虑计算过程的稳定性。分数阶计算的稳定性较为复杂,至今缺乏系统的分析研究。本文采用与二维一阶速度-应力方程时间二阶、空间2N阶精度交错网格有限差分一致的稳定性条件,其近似表达式为[15]
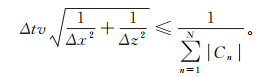 (9)
(9) 式中:Δx和Δz分别为横向和纵向空间网格步长;Δt为时间间隔;v=max{vP//, vP⊥, vS},vP//、vP⊥、vS分别为平行于地层的P波速度分量和垂直于地层的P波速度分量、S波速度分量;Cn为交错网格差分算子系数。
为消除人工边界反射,采用简便实用的Cerjan衰减边界[16],即沿人工边界向外扩充H个网格点,进入扩充区域内的波场通过与因子G相乘逐渐衰减为零。
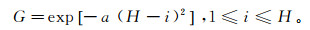 (10)
(10) 式中,a为衰减系数,可通过多次试验确定其最佳值。
3 三种算法及其差分格式对于分数阶波传播方程中的整数阶时间导数和空间导数,采用高阶交错网格有限差分算法进行数值计算。由于交错网格有限差分方法将空间变量的导数在响应网格点之间的半程上进行计算,可以在不增加计算量和内存要求的前提下提高模拟精度,有效减少传统有限差分的网格频散。
对于分数阶波传播方程中的分数阶时间导数,使用Grünwald-Letnikov分数阶导数定义,并分别使用全局记忆法、短时记忆法、自适应记忆法进行数值计算。
采用Grünwald-Letnikov分数阶导数定义,分数阶导数的离散式为
 (11)
(11) 式中,定义函数
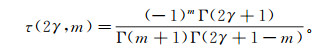
这样,函数τ(2γ, m)有如下递推关系:

特殊地,当m=0时,τ(2γ, 0)=1。
当Δt→0、t=mΔt时,离散化式(11)有
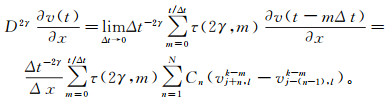 (12)
(12) 式中:Δt为时间步长;(j, l)为空间离散点坐标;k为当前时间迭代次数。
3.1 全局记忆法由于分数阶时间导数具有历史依赖性和空间全域相关特性,所以计算当前时刻的分数阶导数需要用到之前所有时刻的函数值。在式(12)中不对m做任何截断处理,即为全局记忆法,其分数阶导数差分格式即为式(12)。
3.2 短时记忆法短时记忆法通过截断算子长度,仅考虑当前时刻t以前且对当前时刻影响较大的有限时间区间[t-L, t]。对于本文分数阶波传播方程中的分数阶导数,其短时记忆法差分近似式为
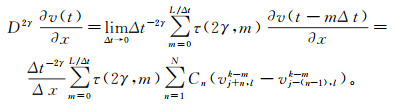 (13)
(13) 对于任意正实数q,设初始间隔[0, q],这一区间内的所有点都参与求和计算,过去时间历程被分为不同长度的区间。第i区间定义为
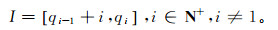 (14)
(14) 对于式(14),定义区间集合为
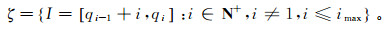
ζ中每个区间内的采样间隔d的集合为
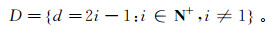
式中,imax为使得k∈I = [qi-1+i, qi]的最大i值。
根据上述定义,本文分数阶波传播方程中分数阶导数应用自适应记忆法的差分近似式为
 (15)
(15) 式中:g∈N+;mi为时间点集
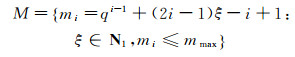
中的元素,mmax为当i=imax时的mi。
4 数值模拟为了对3种方法进行对比分析,选取一个模型进行数值模拟。模型大小为3 000 m×3 000 m。介质物性参数:干燥情况下各向同性背景孔隙介质中vP//=5 600 m/s,vP⊥=5 167 m/s,vS=3 126 m/s,ϕ=0.2,ρs=2 500 kg/m3,ρf=1 040 kg/m3,ρa1=420 kg/m3,ρa3=450 kg/m3,固相体积模量Ks=80 GPa,x方向和z方向渗透率分别为k11=6×10-10m2/s和k33=1×10-9m2/s,η=0.001 Pa·s,P波和S波的品质因子分别为QP=30和QS=15,参考频率ωr=80 Hz。其他计算参数:Δx=Δz=10 m,Δt=5×10-4 s,t=0.2 s。震源子波采用Ricker子波,震源位置为(1 500 m, 1 500 m),主频为40 Hz,在模拟中震源分别为x、z方向集中力源。在网格点坐标为(150, 200)处设置检波点记录固相质点垂直速度分量的时间记录。
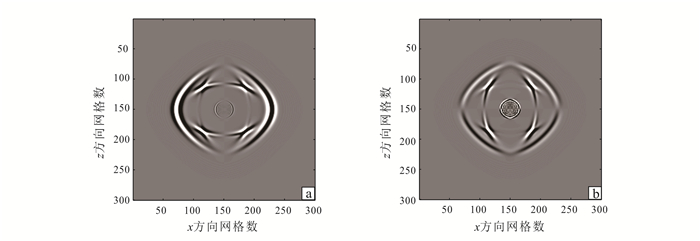
4.1 全局记忆法由于全局记忆法未对分数阶微分算子进行截断处理,在数值模拟上认为是精确的。利用全局记忆法对上述模型进行数值模拟的运行时间和所占用物理内存分别为1 395.965 962 s和5 875 MB。图 1给出了利用全局记忆法对波传播方程进行数值模拟,固相x分量速度和流相z分量速度在t=0.15 s时刻的波场快照。
|
| 图 1 全局记忆法黏滞相界固相速度x分量(a)和流相速度z分量(b)t=0.15 s时波场快照 Figure 1 Vicious phase boundary wavefield snapshots of x-component velocity in solid phase (a) andz-component velocity fluid phase (b) at t=0.15 s by using global memory method |
|
|
为了比较分析不同短时记忆长度对模拟结果的影响,针对上述模型,分别采用L=0.15、0.10、0.05 s三种不同短时记忆长度进行数值模拟,表 1给出了所用时间和内存。从表 1可以看出,随着短时记忆长度的减小,计算所需时间和物理内存都在减小;这是因为采用的短时记忆长度越小,所计算的当前时刻之前的时间节点越少。
| L/s | 运行时间/s | 物理内存/MB |
| 0.15 | 1 250.064 324 | 5 011 |
| 0.10 | 1 032.771 320 | 4 996 |
| 0.05 | 693.631 693 | 4 878 |
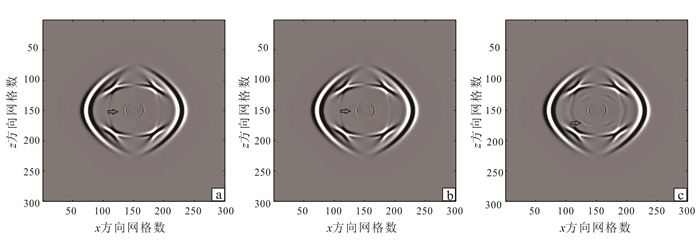
图 2给出了利用3种不同短时记忆长度对波传播方程进行数值模拟,固相x分量速度在t=0.15 s时刻的波场快照,可以看出,随着短时记忆长度的减小,在慢纵波附近(如箭头所指)波场存在明显差异。为了更明显地显示差异,图 3给出了网格点坐标为(150, 200)处不同计算方法固相质点垂直速度分量的时间记录。从图 3可以看出:随着短时记忆长度的改变,快准P波几乎不受影响,而准SV波所受影响较大(图 3b),即:随着采用的短时记忆长度减小,准SV波的精度越来越差。
|
| a.L=0.15 s;b.L=0.10 s;c.L=0.05 s。 图 2 三种不同短时记忆长度黏滞相界固相速度x分量t=0.15 s时波场快照 Figure 2 Vicious phase boundary wavefield snapshots of x-component velocity in solid phase at t=0.15 s by using three different short-term memory lengths |
|
|

|
| 图 3 三种不同短时记忆长度固相质点垂直速度分量时间记录对比图 Figure 3 Comparison of the vertical velocity components of particles with three different short-term memory lengths in solid phase |
|
|
为了比较分析不同初始间隔对模拟结果的影响,针对上述模型,分别采用q=15、10、5三种不同初始间隔进行数值模拟,表 2给出了所用时间和内存。从表 2可以看出,随着初始间隔减小,计算所需时间和物理内存都在增大;这是因为初始间隔越小,之前的时间就会被分成越多的区间,就会有更多的时间节点参与计算。
| q | 运行时间/s | 物理内存/MB |
| 15 | 1 243.499 964 | 4 583 |
| 10 | 1 357.584 104 | 5 083 |
| 5 | 1 461.314 183 | 5 289 |
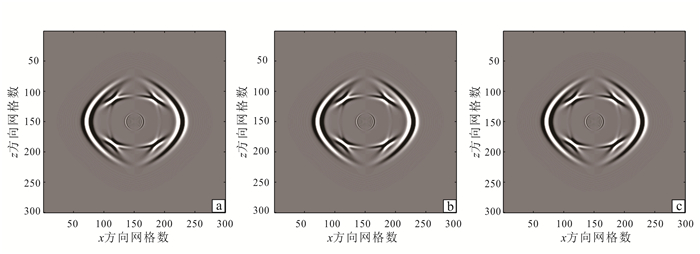
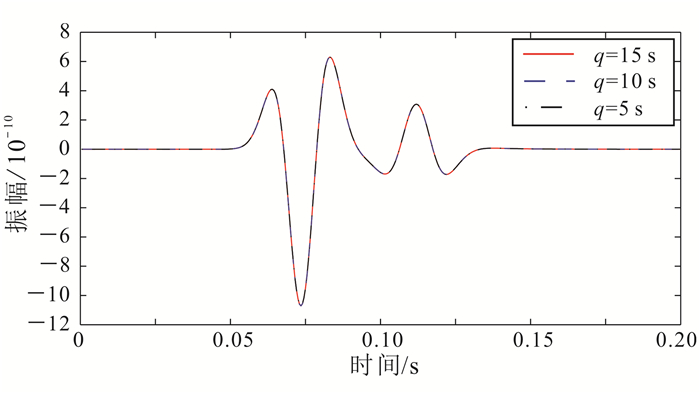
图 4给出了利用3种初始间隔对波传播方程进行数值模拟,固相x分量速度在t=0.15 s时刻的波场快照,可以看出,基于自适应记忆法、采用3种不同初始间隔得到的波场快照无明显差异。为了更明显地显示差异,图 5给出了网格点坐标为(150, 200)处不同计算方法固相质点垂直速度分量的时间记录。从图 4及图 5均可以看出:随着初始间隔的改变,快准P波与准SV波所受影响均较小。因此,当选取初始间隔在稳定性范围内差异相差不悬殊时,自适应记忆法在计算精度上是比较稳定的。
|
| a.q=15;b.q=10;c.q=5。 图 4 三种不同初始间隔黏滞相界固相速度x分量t=0.15 s时波场快照 Figure 4 Vicious phase boundary wavefield snapshots of x-component velocity in solid phase at t=0.15 s by using three different initial intervals |
|
|
|
| 图 5 三种不同初始间隔固相质点垂直速度分量时间记录对比图 Figure 5 Comparison of the vertical velocity components of particles with three different initial intervals in solid phase |
|
|
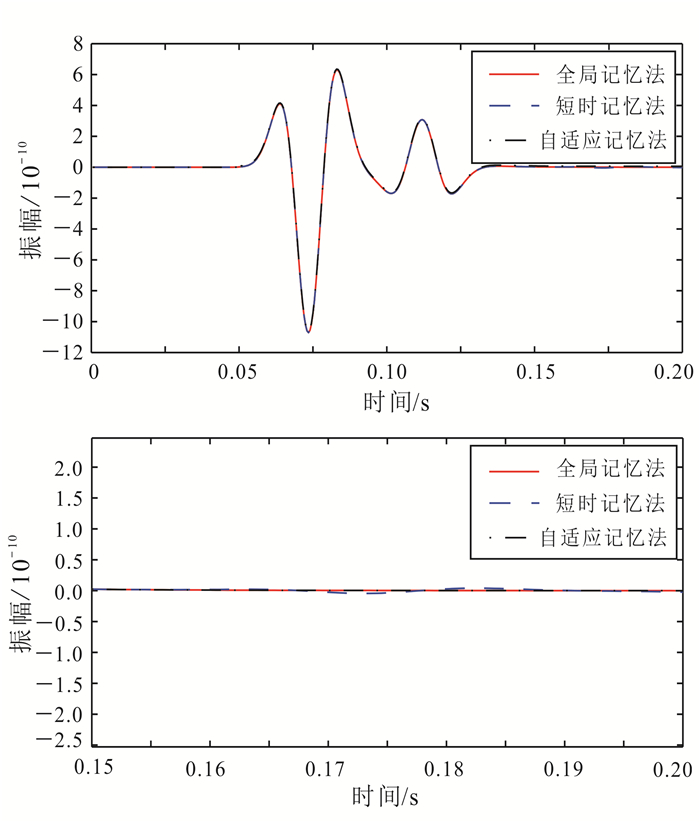
为了比较分析不同分数阶时间导数计算方法对模拟结果的影响,针对上述模型,图 6给出了利用全局记忆法、L=0.1 s短时记忆法和q=10自适应记忆法对波传播方程进行数值模拟,网格点坐标为(150, 200)处固相质点垂直速度分量的时间记录。从图 6可以看出,当L=0.1 s、q=10时,从计算精度上来看,自适应记忆法精度较高,而短时记忆法精度较差。
|
| 图 6 不同计算方法固相质点垂直速度分量时间记录对比图 Figure 6 Comparison of the vertical velocity components of particles with three different numerical methods in solid phase |
|
|
综上:全局记忆法计算当前时刻的分数阶导数需要用到之前所有时刻的值,因此需要较大的计算内存和计算时间,计算效率较低;短时记忆法计算当前时刻的分数阶导数需要用到之前记忆长度L内的所有函数值,所需计算内存和计算时间与记忆长度L的设置有关,短时记忆长度L设置得越短所需计算内存越小,计算时间越短,计算精度越差;自适应记忆法根据对当前时刻分数阶导数值的不同影响程度,在之前的不同时间段内按照加权方式进行抽取,来计算当前时刻的分数阶导数值,随着初始区间减小,计算所需时间和物理内存都增大,但是,初始间隔在数值稳定性范围内,自适应记忆法计算精度较高。因此在3种计算方法中,只有用短时记忆法得出的波场快照在慢纵波附近与其他两种方法得出的波场快照有差别。
5 结论1) 3种计算方法计算的波场中快准P波及准SV波几乎相同,只有慢纵波附近有差别。
2) 全局记忆法需要较大的计算内存和计算时间,计算效率较低;短时记忆法所需计算内存和计算时间与记忆长度的设置有关,记忆长度越大,所需计算内存越大,计算时间越长,计算精度较高;自适应记忆法虽然模拟所需时间与短时记忆法相比较长,所需存储量较大,但是精度更高。
3) 本文在模拟相同模型情况下,对全局记忆法、短时记忆法、自适应记忆法所需的计算内存、模拟精度和所需时间进行了归纳总结,可为后续分数阶时间导数数值模拟及新算法开发和研究提供理论参考基础;对于分数阶时间导数正演问题,需要从模拟精度、模拟所需时间和存储量3个方面进行利弊权衡,从中选出精度较高、存储量较小和模拟所需时间较短的数值计算方法。
| [1] | Biot M A. General Theory of Three-Dimensional Con-solidation[J]. J Appl Phys, 1941, 12: 155-164. DOI:10.1063/1.1712886 |
| [2] | Dvorkin J, Nur A. Dynamic Poroelasticity:A Unified Model with the Squirt and the Biot Mechanisms[J]. Geophysics, 1993, 58: 524-533. DOI:10.1190/1.1443435 |
| [3] | Diallo M S, Appel E. Acoustic Wave Propagation in Saturated Porous Media:Reformulation of the Biot/Squirt Flow Theory[J]. J Appl Geophys, 2000, 44: 313-325. DOI:10.1016/S0926-9851(00)00009-4 |
| [4] | Liu Q R, Katsube N J. The Discovery of a Second Kind of Rotational Wave in Fluid Filled Porous Material[J]. The Journal of the Acoustical Society of America, 1990, 88(2): 1045-1053. DOI:10.1121/1.399853 |
| [5] | Kjartansson E. Constant-Q Wave Propagation and At-tenuation[J]. Journal of Geophysical Research, 1979, 84: 4737-4748. DOI:10.1029/JB084iB09p04737 |
| [6] | Carcione J M. Time-Domain Modeling of Constant-Q Seismic Waves Using Fractional Derivatives[J]. Pure and Applied Geophys, 2002, 159: 1719-1736. DOI:10.1007/s00024-002-8705-z |
| [7] | Podlubny. Fractional Differential Equations[Z]. San Diego: Academic Press, 1999. |
| [8] | Sprouse B P. Computational Efficiency of Fractional Diffusion Using Adaptive Time Step Memory[Z]. Dissertations & Theses-Gradworks, 2010. |
| [9] | Caputo M, Mainardi F. Linear Models of Dissipation in Anelastic Solids[J]. La Rivista del Nuovo Cimento, 1971, 1(2): 161-198. DOI:10.1007/BF02820620 |
| [10] |
林孔容. 关于分数阶导数的几种不同定义的分析与比较[J].
闽江学院学报, 2003, 24(5): 3-6.
Lin Kongrong. Analysis and Comparision of Different Definition About Fractional Integrals and Derivatives[J]. Journal of Minjiang University, 2003, 24(5): 3-6. |
| [11] |
卢明辉, 巴晶, 杨慧珠. 含粘滞流体孔隙介质中的弹性波[J].
工程力学, 2009, 26(5): 36-40.
Lu Minghui, Ba Jing, Yang Huizhu. Propagation of Elastic Waves in a Viscous Fluid-Saturated Prorous Solid[J]. Engineering Mechanics, 2009, 26(5): 36-40. |
| [12] | Yang D H, Zhang Z J. Poroelastic Wave Equation Including the Biot/Squirt Mechanism and the Solid/Fluid Coupling Anisotropy[J]. Wave Motion, 2002, 35(3): 223-245. DOI:10.1016/S0165-2125(01)00106-8 |
| [13] |
刘财, 兰慧田, 郭智奇, 等. 基于改进BISQ机制的双相HTI介质波传播伪谱法模拟与特征分析[J].
地球物理学报, 2013, 56(10): 3461-3473.
Liu Cai, Lan Huitian, Guo Zhiqi, et al. Pseudo-Spectral Modeling and Feature Analysis of Wave Propagation in Two-Phase HTI Medium Based on Reformulated BISQ Mechanism[J]. Chinese Journal of Geophysics, 2013, 56(10): 3461-3473. DOI:10.6038/cjg20131021 |
| [14] | Qiao Z H. Theory and Modelling of Viscoelastic Ani-sotropic Media Using Fractional Time Derivative[C]//78th EAGE Conference & Exhibition 2016. [S. l. ]: EAGE, 2016. |
| [15] |
董良国, 马在田, 曹景忠. 一阶弹性波动方程交错网格高阶差分解法稳定性研究[J].
地球物理学报, 2000, 43(6): 856-864.
Dong Liangguo, Ma Zaitian, Cao Jingzhong. A Study on Stability of the Staggered-grid High-Order Difference Method of First-Order Elastic Wave Equation[J]. Chinese Journal of Geophysics, 2000, 43(6): 856-864. |
| [16] | Cerjan C, Kosloff D, Kosloff R, et al. A Nonref-lecting Boundary Condition for Discrete Acoustic and Elastic Wave Equation[J]. Geophysics, 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |



