0 引言
松辽盆地是位于华北板块、西伯利亚板块和佳木斯地块古生代缝合基底上的一个大型中生代含油气裂谷盆地,具有丰富的油气资源。在新元古代至早二叠世末期,松辽盆地受古亚洲洋构造域控制;在早二叠世末期,海西运动剧烈,南部的华北板块与北部的西伯利亚板块相互碰撞,形成了统一的亚欧板块;在晚三叠世时期,盆地受环太平洋构造域控制,由此形成了统一的松辽汇水盆地[1]。关于松辽盆地的构造演化过程,前人进行了数十年的研究认为,其形成早期主要是受到地幔热流引起的上地幔隆起产生的大陆壳断裂,中晚期主要是受到太平洋板块向亚洲大陆俯冲的控制[2]。目前多数学者认为松辽盆地的构造演化至少经历过两个完整的挤压-拉张旋回[3]。因此,松辽盆地的构造并不是单一机制的结果,多半都是两种以上成因为主导的多期复合的结果[4],这使得松辽盆地的构造情况非常复杂。所以,松辽盆地构造特征的研究变的非常重要,通过对地质构造的分析可以获得构造的动力学环境及成因机制,这对松辽盆地演化过程的研究有很大的帮助。而且在以往的重力资料中可以看出,松辽盆地深部重力异常在东西方向存在明显的重力异常差异,这可能是太平洋板块俯冲滞留体造成的,这需要进一步的研究来验证。
断裂的位置及倾向是描述构造的重要要素,而重力数据的特点就是可以很好地在水平方向上分辨边界的位置,其中应用最早的方法是Evjen[5]1936年提出来的用垂直导数来进行边界识别的方法;后来人们发现水平导数的极大值[6-7]和解析信号的极大值[8]位置与地质体边界也有良好的对应关系,但这些方法都只是适用于浅层的地质体,当地质体的埋深较大时,其不能得出清晰的边界位置。这是因为随着地质体埋深的增加,导数的衰减速度很快。为了解决此问题,在1994年Miller等[9]提出第一个均衡滤波器——tilt angle,此方法可以均衡强弱异常,但是边界识别的效果不是很理想;在2005年Wijns等[10]提出利用总水平导数除以解析信号的值(theta map,也叫θ图法)来进行边界识别;在2015年马国庆等[11]利用构造张量的水平和垂直方向导数定义新的均衡滤波器,解决了无法识别深部异常的问题;2016年周帅等[12]定义了位场数据的三维构造张量,并且基于位场的构造张量同时显示不同振幅异常的边界位置。除了利用重力数据的各阶梯度和张量来进行边界识别,还可以利用数理统计的思想进行边界的确定。2015年徐梦龙等[13]利用各方向均方差相关系数来进行边界识别,这样就避免了用梯度计算时出现的易受干扰、稳定性低的缺点。而本文所提出的倾向成像技术是利用总水平梯度的不对称性来进行倾向识别,所以只能利用含有总水平梯度的方法。本文所用的边界识别方法是增强型局部相位滤波器(incremental local phase filter, ILP)[14],此方法可以在均衡强弱异常的基础上降低高阶导数和垂直导数计算所带来的不稳定性,仅利用一阶和二阶水平导数来构建边界识别滤波器。ILP最大值对应着地质体的边界,该方法具有能够同时识别出不同深度地质体边界的优势,非常适用于大范围勘探中对多个断层同时进行定位的工作。
在倾向识别方面,前人一般都是通过获得倾角大小并利用倾角的正负来确定倾向方向的。最早是Green[15]在1976年提出利用水平梯度和垂直梯度联合解释台阶;1995年Butler[16]将这种方法推广到多个台阶模型解释中;到了2005年,魏伟等[17]通过最小二乘拟合法简化了求解过程,并使结果更加稳定;2006年Cooper[18]提出通过扩展欧拉反褶积与霍夫变换结合的方法获取重磁数据中的倾角,这样虽然可以得到较为精确的倾角信息,但是计算量大而且只适用于台阶厚度已知或下底无限延伸的情况;高秀鹤等[19]在2017年提出角度扫描的方法来拟合出最佳的倾角,从而成功地获得倾向的信息。这些方法共同的缺点是计算复杂,且只能针对单一的地质体进行计算,很难应用于大范围的重力勘探,而且他们研究目的只是让断层的倾角角度计算更加精确,并没有对倾向的问题进行更加深入的讨论。当勘探目的并不是对于单一断层而是针对一定范围内的所有断层时,以上的倾向或倾角识别方法都不实用,这时我们需要一种可以针对多个断层同时显示断层倾向的方法。
本文主要的研究内容就包括提出一种新的方法,利用重力异常的总水平导数极值两侧的不对称性与倾向的关系可以同时对多个断裂进行倾向的识别,断裂水平导数变化率较小的一侧指示断裂的倾向,因此可直接标识出断裂的特征,减少了多断裂边界与倾向识别的时间。将此方法应用于松辽盆地的实测重力异常处理,获得了盆地的构造特征,这对于分析松辽盆地构造演化过程具有很重要的意义。并且,本文还以地震数据为约束,利用重力数据进行松辽盆地地层界面的反演,证明松辽盆地重力异常差异的原因是松辽盆地莫霍面下方存在一个界面,且由于太平洋板块的俯冲造成界面在松辽盆地发生了较大的起伏,从而呈现异常的变化,进一步验证了太平洋板块俯冲对于松辽盆地形成具有重要的作用。
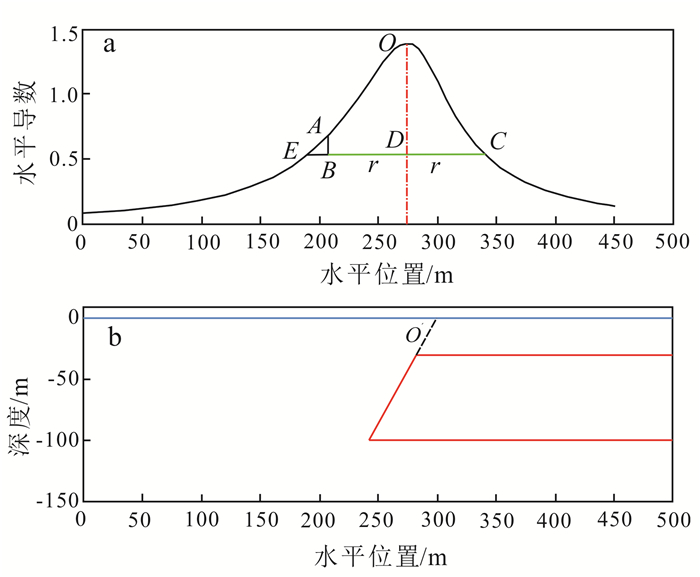
1 原理在实际数据解释中,通过倾斜台阶来模拟断层。图 1a为倾斜台阶正演重力异常的水平导数图,O为水平导数的极值位置,D与O在同一水平位置上,A、C都是水平导数曲线上的点,B与A在同一水平位置上。B、D、C在同一水平面上。倾向成像技术的原理就是当倾斜台阶的倾向向着x轴负方向时,在它的正演异常水平导数曲线中DB=DC=r;则距离极值的水平位置为r处的2个水平导数值大小不同,如果有一确定的水平线(如BDC所在的水平线)截断水平导数异常曲线,则水平线和异常水平导数曲线2个交点水平位置与极值水平位置的距离不同(即ED与DC的长度不同),距离大的交点所在方向为断层的倾向方向。我们只需要证明A点的纵坐标大于C点的纵坐标即可得出ED>DC的结论。
|
| 图 1 倾斜台阶正演重力异常的水平导数 Figure 1 Horizontal derivative of fault anomalies |
|
|
断层的重力异常等价于倾斜台阶,所以我们可以用倾斜台阶的公式来推导断层的性质。因为倾向成像技术是在区域异常中选取每个剖面进行成像后汇总在区域异常图中,所以我们利用二维的剖面公式来推导倾向成像的原理,当坐标原点是倾斜台阶倾斜面的反向延长线与地面的交点时(图 1b),倾斜台阶重力异常的水平导数(Vxz)理论公式[20]如下:
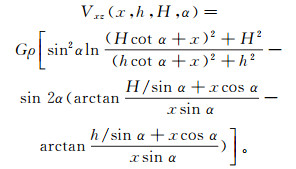 (1)
(1) 式中:h、H分别为倾斜台阶的上底与下底埋深;α为倾斜台阶的倾角;x为水平方向的距离;G是万有引力常数;ρ为剩余密度。
由上式可以推导出倾斜台阶的重力异常水平导数的极值x0为
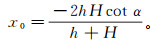 (2)
(2) 当r>0(r为图 1a中DC间的距离)时,令
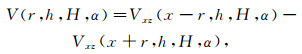 (3)
(3) 且
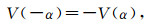 (4)
(4) 因此,若能证明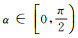
令式(3)对r求偏导的值为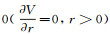
 (5)
(5) 且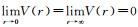
所以可以得到:
 (6)
(6) 其中,
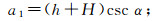 (7)
(7) 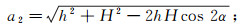 (8)
(8) 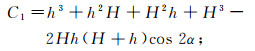 (9)
(9) 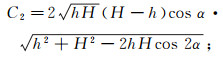 (10)
(10) 设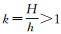
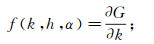 (11)
(11) 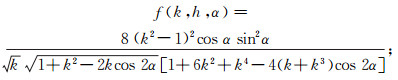 (12)
(12) 因为
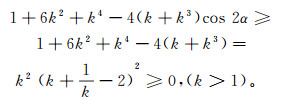 (13)
(13) 所以f(k, h, α)>0时,G(k, h, α)在k∈(1, +∞)上随着k单调递增。
因为G(1, h, α)=0,所以k>1时G(k, h, α)>0,即V(r0, H, h, α)>0,由以上公式可以得出结论:V(r, H, h, α)在r>0范围内有且仅有一个极值点且大于0,而V(0)=V(∞)=0;对于r>0, V(r)>0,理论成立。
本文提出的倾向成像技术具体步骤分为以下几步:
1) 对原始重力异常进行总水平导数计算,因为水平导数不像垂直导数一样对噪声有很强的放大作用,所以实际应用离散数据计算时产生的误差可以忽略,对之后的计算没有影响。
2) 找到总水平导数数据中极大值的位置并标记为O。
3) 依据所测区域的断层异常,给出截断平面的位置坐标yD(即图 1中D点的纵坐标),这是一个经验参数,一般取总水平导数的算数平均值,可以依据成图效果进行改动,尽量做到去除截断平面以下的数据后所剩的异常涵盖了全区的断层,并且没有多个断层的异常完全连接在一起。当取值过小时断层之间的影响会变大使得结果不准确,当取值较大时会筛选掉一部分幅值较低的断层使得获得的倾向信息减少。
4) 去除截断平面以下的数据,并且提取剩余数据边界点的位置(即图 1中的A、C)。
5) 对每一个O点都找到一个相对应的距离最近的边界点P,OP的反向延长线方向即为断层的倾向方向,并且将反向延长线的长度设为与OP相同,这对之后实际数据处理的改进有很大的作用。如果距离最近的边界点有多个,说明此处断层为近垂直断层或者此处是多个断层异常相交区域。
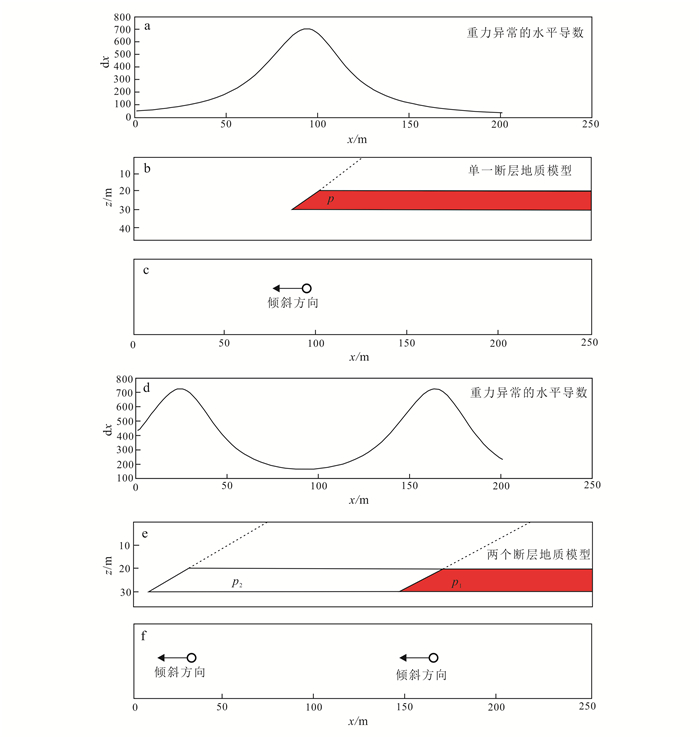
2 模型试验图 2为单一断层与双断层模型倾向成像结果。图 2a、d为模型正演的重力异常水平导数,图 2b、e为模型在地下位置示意图,图 2c、f为倾向成像计算的结果。图 2b中的倾斜台阶为倾角30°,埋深20~30 m;而图 2e中的2个倾斜台阶为相距140 m的2个倾角30°,埋深20~30 m。在计算过程中,利用倾向与异常的水平导数之间存在的联系,我们首先进行了单一倾斜台阶的模型试验。图 2c为倾角是30°的倾斜台阶进行倾向成像处理的结果。圆点所在位置为计算得出的水平导数极大值点在平面坐标上的投影位置,表示断裂的位置。箭头用来指示台阶倾向。由此可知,图 2中的倾斜台阶倾向为x轴的负方向。可以看出,对于单一的断层模型,此技术可以准确地反演出断层的倾向。
|
| a、b、c.倾角30°,埋深20~30 m;d、e、f.相距140 m的两个倾角30°,埋深20~30 m。 图 2 倾斜台阶理论模型倾向成像结果 Figure 2 Dip imaging technology apply to theory model of faults |
|
|
对于2个断层的模型试验,结果为图 2f。图 2d中为2条相平行断层剖面的水平导数异常图,角度都为30°,埋深(分别为上顶埋深与下底埋深)为20~30 m。由图 2f中的结果可以看出,倾向成像技术反演出的倾向与模型信息一致。需要注意的是,如果2个平行断层相距很近,会互相产生干扰。
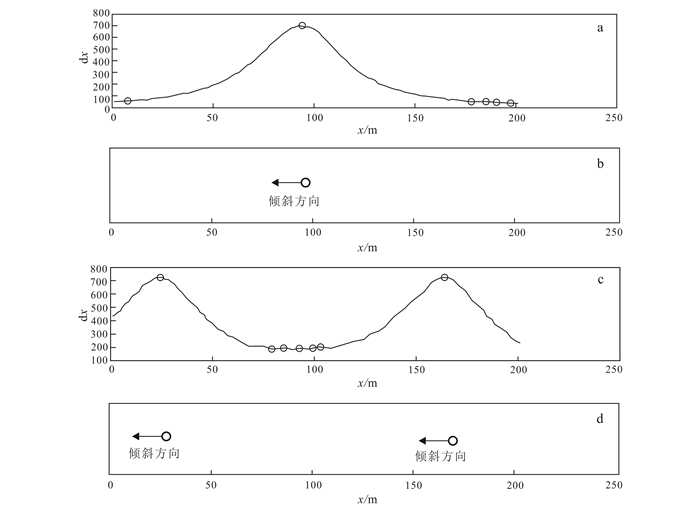
为了检验本方法的稳定相与噪声对结果的误差影响,本文对图 2中的理论模型增加了噪声。图 3为对理论模型进行加噪声处理的倾向成像结果图,其中增加信噪比为80%的噪声,这使得异常水平导数不是很光滑,含有一些小的高频抖动。但是由于本程序选取极大值的方式使得只有选取点的异常值比周围4个点都大时才被看作极大值点(图 3中用圈标出)。但是由于噪声的影响还是会使极大值选取产生误差,如图 3中曲线较为平坦的地方会出现假的极大值位置。这只是在台阶异常导数的边界或者多个台阶之间,所以产生假的极大值的位置都是水平导数值较小的部分,这部分极大值点会在对水平导数进行截断处理去除平均值以下部分的过程中去除掉。所以并不影响结果的准确性。只有当噪声大到可以影响真极大值附近的极大值选取时才会使结果产生误差。从图 3b、d的结果中可以看出,此方法在含有噪声的情况下获得结果是断层倾向向着x轴负方向,与模型一致。总体来说,此方法在异常中存在噪声时也可以获得良好的效果。
|
| a.倾角30°,埋深20~30 m;b.相距140 m的两个倾角30°,埋深20~30 m。 图 3 倾斜台阶理论模型(含噪声)倾向成像结果 Figure 3 Dip imaging technology apply to theory model (including noise) of faults |
|
|
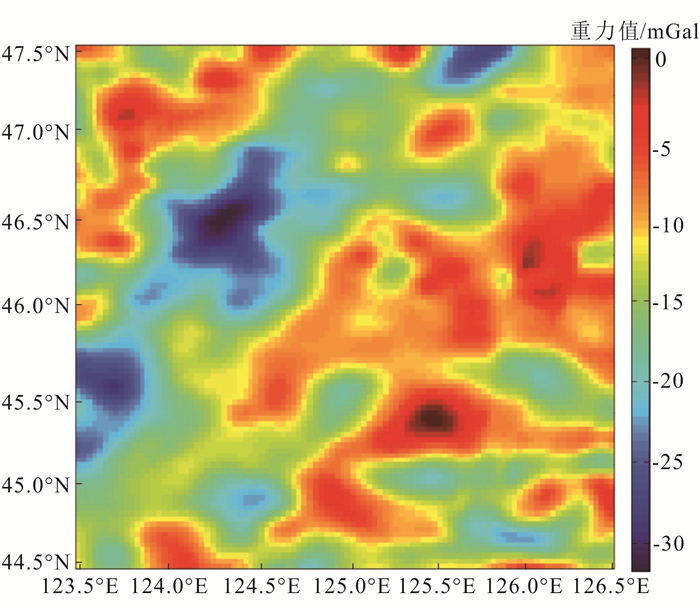
本文所用的实际数据是搜集来自整个东北地区重力数据中截取的松辽盆地北部区域的重力异常数据(图 4),此区域长约238 km,宽约334 km,一共有1万个重力数据点。并且,在数据应用之前已经进行了去噪处理,从而减小了噪声对结果的影响。
|
| 图 4 松辽盆地原始重力异常 Figure 4 Original gravity anomaly map of Songliao basin |
|
|
在实际数据处理中,存在各种干扰与误差,所以需要对方法的稳定性与容错性进行提高。因为在垂直断层情况下,重力异常的水平导数曲线左右对称,所以随着倾角变大并接近于90°,图 1中ED与DC的差值接近于0。这说明随着倾角的变小,B点与边界点(E)的距离逐渐变远,误差与干扰对倾向的影响也会变小,所以只要以此为依据,把对倾向影响相对较大的点去掉即可。
以图 1为例,所以本文所用的方法是,在倾向成像技术处理后,以B点为中心,r1为半径的圆形区域内搜索(此圆与水平面平行,在图 1中相当于搜索x∈[xB-r1,xB+r1]范围内,xB为B点横坐标),查看是否含有截断后的边界点,如果含有边界点说明B点与边界的距离较小。这样就可以找到倾向受干扰较大的点,从而去掉容错率较低的点所算出的结果,加强了结果的可信度。这里的干扰大小是依据实际测量与成图情况确定的经验参数,由r1的大小来控制,随着r1的增加得到的结果会更加可信,但是有用的信息也会被除去,所以r1要在满足稳定的条件下尽量地小一些。
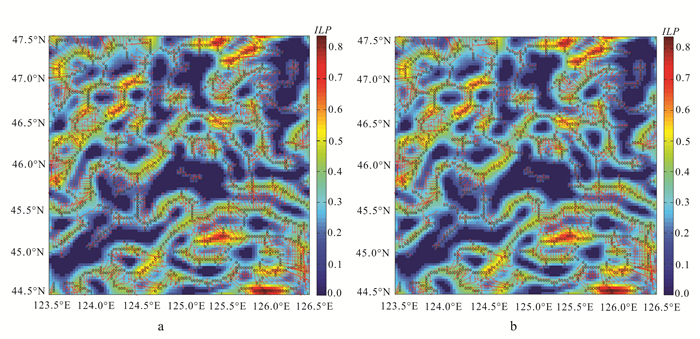
为了检验改进工作的效果,本文对松辽盆地北部区域的重力异常进行倾向成像结果的对比,下面图 5分别为r1=0、r1=2的实际数据成图。由图 5可以看出,随着r1的增加,各个极值点的倾向更加一致,但是倾向信息会逐渐减少。所以实际资料处理时要综合考虑来选取r1的值。
|
| a.r1=0;b.r1=2。ILP.利用ILP方法获得的数值。 图 5 倾向成像技术应用于松辽盆地效果 Figure 5 Dip imaging technology apply to Songliao basin |
|
|
图 6为松辽盆地北部区域重力异常在ILP边界识别后结合倾向成像技术的结果图,图中的地区以大庆为中心,南到松原,北到明水,东西方向在齐齐哈尔与绥化之间。图中的黑色圆圈用于指示断裂的位置,红线用于指示断裂的倾向,断裂倾向朝向红线所在的一侧。当同一条断裂中大多数红线指示方向一致时,我们就认为这条断裂的倾向与大多数红线指示一致并且垂直于断裂的走向方向;当同一断裂中多条红色指示线没有明确指向断裂的某一侧或没有红色指示线时,我们认为这条断裂是近垂直的断裂。由图 6知,倾向成像技术可以同时观测到多条断裂的倾向信息,并且明确地表现出来,在实际应用中获得了很好的效果。当此项技术与ILP边界识别结合在一起时可以获得这一区域的不同深度的断裂位置与倾向信息,从而得到研究区域的断裂与倾向的俯视图,我们依据图 6制作了此区域断裂倾向成像技术结果的示意图(图 7)。

|
| r1=1。 图 6 松辽盆地重力异常在ILP边界识别后结合倾向成像技术的结果 Figure 6 Dip imaging technology apply to Songliao basin gravity anomaly's improved local phase filter results |
|
|
|
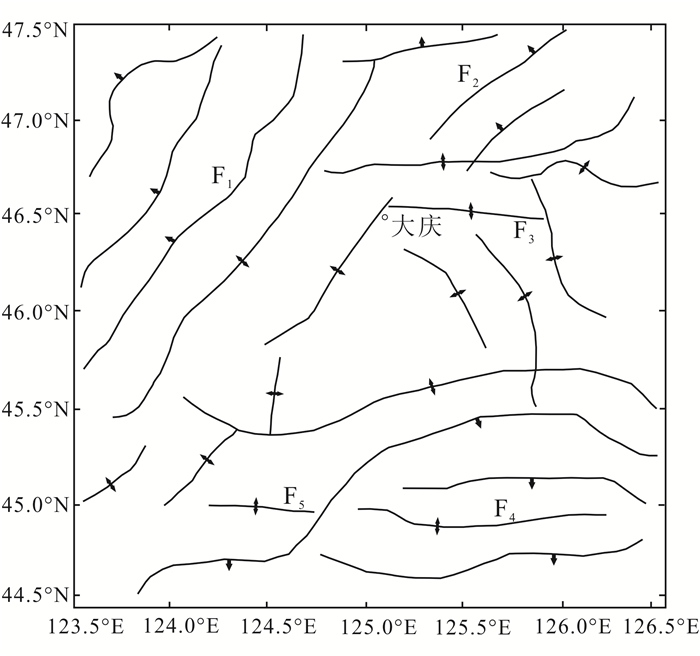
| F1.富裕—泰来断裂;F2.德都—大安断裂;F3.明水断裂;F4、F5.大安—扶余断裂。 图 7 断裂倾向成像技术结果 Figure 7 Dip imaging technology result |
|
|
图 7为将倾向成像技术应用到松辽盆地中部区域的重力异常中的效果图,此效果图是由图 6中的倾向成像结果提取出来的,从图中箭头的指示可以明显地分辨出各个断层的倾向。可以看出倾向成像技术在实际应用中可以有效地识别构造特征,F1(富裕—泰来断裂)与F2(德都—大安断裂)的倾向明显是北西向,而F3(明水断裂)由于与附近断层距离很近会受到影响,但也可以依据黑线左端的非异常叠加区域判断出它是近垂直断裂,F4、F5(大安—扶余断裂)也可以明显看出属于垂直断裂,并且这个东西走向的断裂被南北向断裂截断,明显是松辽盆地中后期受到太平洋板块俯冲的影响。而其他断层也可以在图 7中明显地判断出倾向与走向,西北区域断层主要的走向为北东向,倾向西北,而中部区域主要是垂直断层,并且这一区域断层之间的相互切割比较严重,断层多被分为许多小段。可以看出松辽盆地主要受北东向断裂的控制,倾斜方向多数为北西向,盆地断裂倾向明显受到西太平洋板块俯冲的影响并具有明显的断陷盆地特征,此外该地区为西太平洋和西伯利亚板块作用的汇聚地带,部分断裂呈现出近似直立的状态。
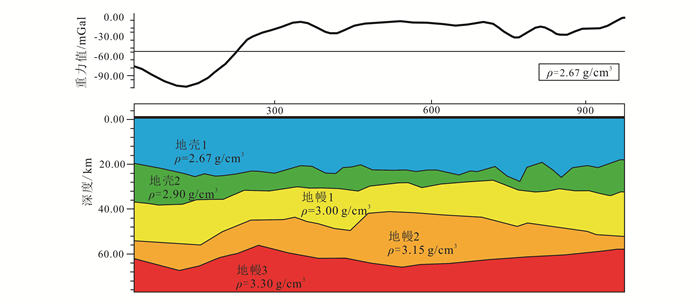
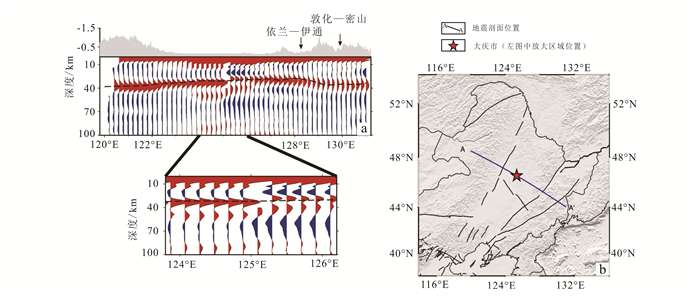
4 松辽盆地莫霍面特征分析图 8是以地震数据为约束,利用重力数据进行松辽盆地地层界面的反演结果。图 9中的地震数据为天然源地震勘探获得的结果,剖面从呼伦贝尔市到牡丹江市,星号位置为大庆市。图 8中所用的重力数据与地震剖面位置一致,为从东北的重力异常中截取出来的重力剖面数据。由图 8、图 9可以看出,图 9a中地震数据显示的莫霍面位于30~40 km处(图 9中虚线),与图 8中的地壳2和地幔1之间的界面一致。但是地震数据显示,莫霍面以下还存在一个强反射界面,从地震数据中可以判断这一界面在40~60 km深度,并且两端延伸到124°E与126°E处渐渐与上一界面合为一个界面,说明这个强反射界面可能属于一个由地壳剥离出来的块体。但是这样的界面特征难以解释此剖面的重力异常在东西两侧存在的明显差异,所以本文以地震数据为约束,利用重力数据进行松辽盆地的界面反演进行验证,来确定这个强反射界面是否属于拆沉作用产生的上覆地壳剥离。通过图 8中的结果可以看出,莫霍面以下的强反射界面向两侧延伸较远,并不属于拆沉作用的效果,可能是由于莫霍面的影响使得与莫霍面距离较近的反射界面难以在地震数据中显示出来。所以依据界面反演结果可以推断出,这一强反射界面是由太平洋板块俯冲造成的,处于太平洋板块俯冲到欧亚大陆板块后再融于地幔的时期,并且由于太平洋板块的俯冲作用造成界面在松辽盆地发生了较大的隆起,从而使得重力异常变化明显。
|
| ρ为密度。 图 8 东北地区重力剖面人机交互界面反演图 Figure 8 Interactive inversion of gravity anomaly in Northeast China |
|
|
|
| 图 9 东北地区地震剖面图(a)及剖面位置显示图(b) Figure 9 Seismic profile of Northeast China(a) and the position of profile(b) |
|
|
1) 本文提出的倾向成像技术可有效地识别构造的特征,并将其应用于松辽盆地的构造识别,可以看出松辽盆地构造大多呈现西北倾向,主要是由于西太平洋板块俯冲所带来的影响;此外,该地区为西太平洋和西伯利亚板块作用的汇聚地带,部分断裂呈现出近似直立状态。
2) 以地震数据为约束,利用重力数据进行松辽盆地地层界面的反演,获得了莫霍面及以下的界面特征,证明松辽盆地东西两侧重力异常差异明显的原因是松辽盆地莫霍面下方十几千米还存在一个界面,由于太平洋板块的俯冲作用造成界面在松辽盆地发生了较大的隆起,从而呈现异常的变化。
| [1] |
曹金华. 松辽盆地综合地球物理剖面地质解释[D]. 长春: 吉林大学, 2017.
Cao Jinhua. Geological Interpretation of Integrated Geophysical Profile in Songliao Basin, NE China[D]. Changchun: Jilin University, 2017. |
| [2] |
侯启军, 冯志强, 冯子辉.
松辽盆地陆相石油地质学[M]. 北京: 石油工业出版社, 2009.
Hou Qijun, Feng Zhiqiang, Feng Zihui. Petroleum Geology of Continental Facies in Songliao Basin[M]. Beijing: Petroleum Industry Press, 2009. |
| [3] |
王金臣. 松辽盆地古中央隆起带基底构造特征研究[D]. 长春: 吉林大学, 2016.
Wang Jinchen. Study on the Basement Structure Characteristics of the Paleo Central Uplift Belt[D]. Changchun: Jilin University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10183-1016078941.htm |
| [4] |
曹怀仁. 松辽盆地烃源岩形成环境与页岩油地质评价研究[D]. 北京: 中国科学院大学, 2017.
Cao Huairen. The Paleo-Environment of Source Rock Formation and Geological Evaluation of Shale Oil in Songliao Basin[D]. Beijing: University of Chinese Academy of Sciences, 2017. http://cdmd.cnki.com.cn/Article/CDMD-80165-1017074635.htm |
| [5] | Evjen H M. The Place of the Vertical Gradient in Gravitational Interpretations[J]. Geophysics, 1936, 1(1): 127-136. DOI:10.1190/1.1437067 |
| [6] | Cordell L, Grauch V J S. Mapping Basement Mag-netization Zones from Aeromagnetic Data in the San Juan Basin, New Mexico[J]. Seg Technical Program Expanded Abstracts, 1982, 1(1): 520. |
| [7] | Cordell L. Gravimetric Expression of Graben Faulting in Santa Fe Country and the Espanola Basin, New Mexico[J]. Science, 2014, 192: 43-43. |
| [8] | Roest W R, Verhoef J, Pilkington M. Magnetic Inter-pretation Using the 3-D Analytic Signal[J]. Geophysics, 1992, 57(1): 116-125. DOI:10.1190/1.1443174 |
| [9] | Miller H G, Singh V. Potential Field Tilt:A New Co-ncept for Location of Potential Field Sources[J]. Journal of Applied Geophysics, 1994, 32(2): 213-217. |
| [10] | Wijns C, Perez C, Kowalczyk P. Theta Map:Edge Detection in Magnetic Data[J]. Geophysics, 2005, 70(4): 39-43. DOI:10.1190/1.1988184 |
| [11] | Ma Guoqing, Liu Cai, Huang Danian. The Removal of Additional Edges in the Edge Detection of Potential Field Data[J]. Journal of Applied Geophysics, 2015, 114: 168-173. DOI:10.1016/j.jappgeo.2015.01.007 |
| [12] |
周帅, 黄大年, 焦健. 基于三维构造张量的位场边界识别滤波器[J].
地球物理学报, 2016, 59(10): 3847-3858.
Zhou Shuai, Huang Danian, Jiao Jian. A Filter to Detect Edge of Potential Field Data Based on Three-Dimensional Structural Tensors[J]. Chinese Journal of Geophysics, 2016, 59(10): 3847-3858. |
| [13] | Xu Menglong, Yang Changbao, Wu Yangang, et al. Edge Detection in the Potential Field Using the Correlation Coefficients of Multidirectional Standard Deviations[J]. Applied Geophysics, 2015, 12(1): 23-24. |
| [14] |
马国庆. 位场(重 & 磁)及其梯度异常自动解释方法研究[D]. 长春: 吉林大学, 2013.
Ma Guoqing. The Study on the Automatic Interpretation Methods of Potential Field(Gravity & Magnetic)and Its Gradients[D]. Changchun: Jilin University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10183-1013193728.htm |
| [15] | Green R. Accurate Determination of the Dip Angle of a Geological Contact Using the Gravity Method[J]. Geophys Prosp, 1976(24): 265-272. |
| [16] | Butle D K. Generalized Gravity Gradient Analysis for 2D Inversion[J]. Geophysics, 1995, 60(4): 1018-1028. DOI:10.1190/1.1443830 |
| [17] |
魏伟, 刘天佑. 梯度法解释复杂二维断裂重力异常[J].
物探与化探, 2005, 29(4): 347-350.
Wei Wei, Liu Tianyou. Interpretation of Complex Two-Dimensional Fault Gravity Anomalies by Gradient Method[J]. Geophysical and Geochemical Exploration, 2005, 29(4): 347-350. |
| [18] | Cooper G R J. Obtaining Dip and Susceptibility Infor-mation from Euler Deconvolution Using the Hough Transform[J]. Computers and Geosciences, 2006, 32(10): 1592-1599. DOI:10.1016/j.cageo.2006.02.019 |
| [19] |
高秀鹤, 黄大年, 孙思源, 等. 重力梯度数据协克里金三维反演确定岩脉倾向[J].
吉林大学学报(地球科学版), 2017, 47(2): 589-596.
Gao Xiuhe, Huang Danian, Sun Siyuan, et al. Identify the Dip Angle of the Dipping Dike Model Based on Cokriging Inversion of Gravity Grandient Data[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(2): 589-596. |
| [20] |
李丽丽, 孟令顺, 杜晓娟, 等. 一种断层重力异常定量解释方法[J].
石油地球物理勘探, 2012, 47(4): 665-667.
Li Lili, Meng Lingshun, Du Xiaojuan, et al. A Quantitative Interpretation Method for Gravity Anomaly of Faults[J]. Oil Geophysical Prospecting, 2012, 47(4): 665-667. |


