0 引言
20世纪70年代以来, 在电子技术以及数据处理技术发展的推动下, 受政治以及军事需求的影响, 探地雷达技术开始得到飞速发展。相比于美国、加拿大、瑞典等国相继研发的商用时域脉冲探地雷达, 频域探地雷达的发展速度较为缓慢:1974年, Robinson等[1]首次应用步进频率信号作为探地雷达的发射信号, 开启了频域探地雷达的研究工作; 1984年, Lizuka等[2]对步进频率探地雷达的原理与方法做出详细介绍。20世纪90年代后, 价格低、体积小的商用仪器随着电子元件的快速发展得到了进一步开发和应用。频域探地雷达系统的构建也随着微电子技术、材料学技术以及数字处理技术的发展进入了崭新阶段。
近年来, 步进频率探地雷达越来越多地应用于雷达的相关研究工作中[3-8], 各大科研院所及高等学校构建了以矢量网络分析仪为主体的步进频率探地雷达, 在不断发展和改进硬件系统性能的同时, 进行探地雷达天线性能分析、目标体属性分析、目标体识别等工作[9-10]。本研究基于多种极化模式天线布局的时间同步性, 利用开关控制器及同轴开关对原有矢量网络分析仪的双通道进行扩展与开发, 旨在实现多种极化模式天线宽频带信号多通道发射及多通道接收的目的, 以提高探测优势和时间效率。
1 步进频率探地雷达工作原理步进频率探地雷达系统(step frequency ground penetrating radar, SFGPR)是频率域雷达系统的典型代表, 是以阶梯形式步进的连续波雷达。SFGPR在频率域实现信号的发射和采集, 获得地下目标体响应的频率域复信号, 即振幅与相位信息, 通过傅里叶变换的方法获得地下目标体的响应特征。频率域雷达发射信号的起始频率为fstar, 在一个扫描周期内, 信号以固定频率间隔Δf逐步上升至终止频率fstop 。工作频带宽度为B=fstop-fstar ,频率间隔为Δf=B/(N-1), N为步进频点数, 步进频率波形则表示为N个频率递增的脉冲叠加。
2 多发射多接收极化步进频率探地雷达系统设计及实现基于电磁波理论, 高频率的电磁波可获得高的空间分辨率信息, 具有宽频带特征的极化探地雷达系统, 又具有区分目标特征能力强、抗干扰能力强的优势。宽频带信号的发射需要较长时间来完成, 频带越宽, 所耗时间越长。在实际探测应用中, 为了获得探测目标的多维度信息, 多采用多种极化模式的天线组合, 在宽频带信号源的配合下来综合完成目标丰富信息的获取。在实际探测的天线布置工作中, 这种多极化模式天线的探测方式, 若分步多次布置多种模式极化天线, 耗时较长, 在一定程度上影响了探测效率, 且由于天线重复定位精度的影响, 将给高精度目标探测引入外部误差。若能一次性地将多种极化天线同时布置到位, 不仅可以提高探测时间效率, 且可有效控制天线位置误差所带来的影响。基于多种极化模式天线布局的时间同步性设计思想与设计原则, 利用开关控制器及同轴开关对原有矢量网络分析仪的双通道进行扩展与开发, 旨在实现多种极化模式天线宽频带信号多通道发射及多通道接收的目的, 以提高探测优势和时间效率。
以矢量网络分析仪为核心构建的多输入多输出极化步进频率探地雷达系统如图 1。该系统主要由计算机、矢量网络分析仪、三维直角坐标仪、开关控制转换器及同轴开关、极化天线及天线阵列、同轴电缆等组成(表 1)。其中:三维直角坐标仪定位范围为3.3 m×3.3 m×1.2 m, 位置定位精度可实现0.1 mm; 矢量网络分析仪可发生9.0 kHz~8.5 GHz的电磁波信号, 满足宽频带特征的极化探地雷达系统的实现。

|
| 图 1 多输入多输出极化步进频率探地雷达硬件系统实物图 Figure 1 Photograph of multiple-input and multiple-output polarimetric stepped-frequency ground penetrating radar system |
|
|
| 组件 | 型号 | 技术指标 | 功能 |
| 矢量网络分析仪 | Agilent E5071C | 9.0 kHz~8.5 GHz | 发射、接收电磁波信号 |
| 三维直角坐标仪 | 自研 | 定位精度0.1 mm | 天线位置精确定位 |
| 开关控制转换器 | Agilent 11713C | 驱动同轴开关, 选择工作通道 | |
| 同轴开关 | Agilent L7106A | 扩展发射及接收通道至6个 | |
| 同轴电缆 | SUCOFLEX | 0.01~18.00 GHz | 连接矢量网络分析仪与同轴开关, 同轴开关与天线 |
| 极化天线 | Vivaldi | 1.2~8.5 GHz | 辐射与接收电磁波 |
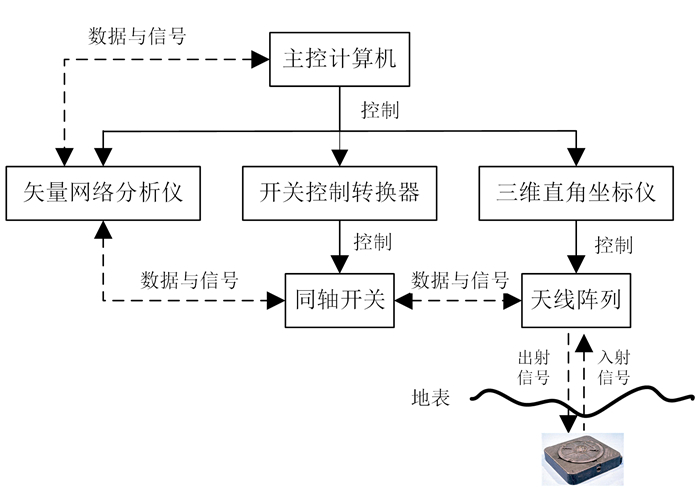
如图 2所示:计算机通过LAN(local area network)线与双通道矢量网络分析仪相连接, 用以控制双通道矢量网络分析发射和接收电磁波并传输数据; 双通道矢量网络分析仪通道端口通过同轴电缆与开关中心端口相连接, 开关通过同轴电缆与天线阵列相连接作为发射端和接收端; 开关控制器给开关供电, 同时选择接收通道, 即选择接收某一接收天线的数据。
|
| 图 2 多输入多输出极化步进频率探地雷达系统工作框图 Figure 2 Diagram of multiple-input and multiple-output polarimetric stepped-frequency ground penetrating radar system |
|
|
工作流程:计算机发出指令, 双通道矢量网络分析仪的1通道发射电磁波, 开关控制器进行发射通道选择, 发射天线发射电磁波; 接收天线接收由目标体散射后产生的回波信号, 开关控制器进行接收通道选择; 同轴开关将信号转换为数据传回矢量网络分析仪2通道, 网络分析仪将数据传回计算机, 计算机进行存储和分析。
3 多次覆盖极化天线阵列布局分析本文构建了一种信号多次覆盖的极化天线阵列, 如图 3所示, 是基于“口字形”组合模式为基本单元构建而成的矩形天线阵列。

|
| 图 3 极化天线阵列实物图 Figure 3 Photograph of polarimetric antenna array |
|
|
在此借鉴勘探地震中的多次覆盖技术, 用天线阵列采集共中心点(CMP)数据, 通过叠加CMP数据来压制噪音, 提高系统测量信噪比。
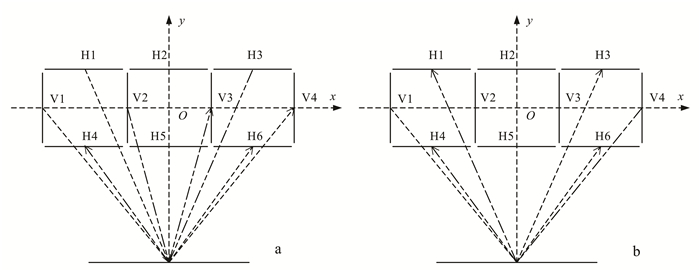
图 4为矩形极化天线阵列实现信号多次覆盖的原理示意图。天线阵列位于雷达探测坐标系下, O(0, 0)为坐标轴原点, 即天线阵列中心坐标点, x轴为测线方向, V1—V4为垂直于测线方向的单个天线单元, H1—H6为沿测线方向的单个天线单元。
|
| a.共极化方式; b.交叉极化方式。 图 4 极化天线阵列工作示意图 Figure 4 Diagram of polarmetric antenna working |
|
|
图 4a是两种共极化模式(HH, VV)下实现信号多次覆盖的原理示意图。
1) HH极化模式下, 两次信号覆盖工作方式为:H1发射H6接收, H3发射H4接收, 对于水平层状介质, 其反射点位于O点正下方。
2) VV极化模式下, 两次信号覆盖工作方式为:V1发射V4接收, V2发射V3接收, 对于水平层状介质, 其反射点也位于O点正下方。
基于此, HH与VV两种共极化模式的CMP位于O点, 即对于水平层状介质, 探测点位于O点正下方。
图 4b是两种交叉极化方式(HV, VH)下实现信号多次覆盖的工作原理示意图。相比于共极化模式(HH, VV), 交叉极化模式更细致地分为上VH、下VH、上HV与下HV共4种子模式。
1) 上VH极化模式下, 两次信号覆盖工作方式为:V1发射H3收, V4发射H1接收, 对于水平层状介质, 其反射点位于(0, 0.25l)正下方处, 其中l为天线宽度。
2) 下VH极化模式下, 两次信号覆盖工作方式为:V1发射H6接收, V4发射H4接收, 对于水平层状介质, 其反射点位于(0, -0.25l)正下方处。
同理:
3) 上HV极化模式下, 两次信号覆盖工作方式为:H1发射V4接收, H3发射V1接收, 对于水平层状介质, 其反射点位于(0, 0.25l)正下方处。
4) 下HV极化模式下, 两次信号覆盖工作方式为:H4发射V4接收, H6发射V1接收, 对于水平层状介质, 其反射点位于(0, -0.25l)正下方处。
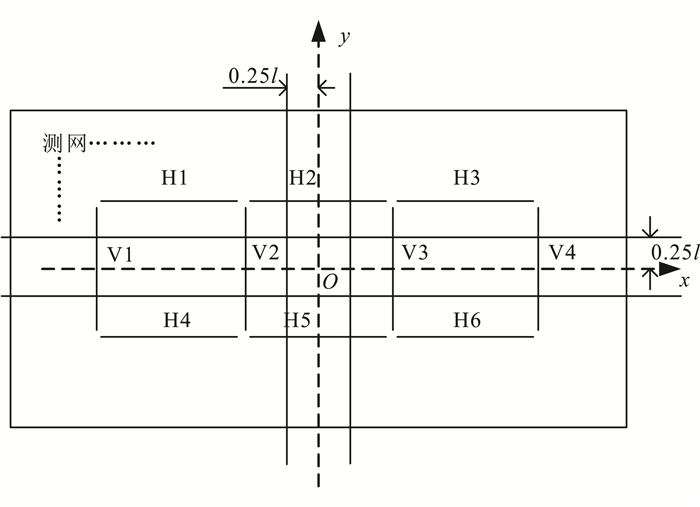
由此可见, 在不同模式的交叉极化方式下, 其目标反射点是不一致的, 具有4个不同的坐标位置, 其间距为0.25l, 且每个反射点均与共极化模式下的目标反射点也不同。因此, 在极化雷达测量过程中, 为了便于实现共反射点的多次覆盖, 实现极化雷达探测方式的本质优势, 测网的设计应遵循以下原则, 即测线间距为0.25l, 测点间距为0.25l, 如图 5所示。
|
| l为天线宽度。 图 5 极化天线阵列测网示意图 Figure 5 Detection network design of polarmetric antenna working |
|
|
步进频率探地雷达(SFGPR)系统所获取的原始数据都是频率域数据。数据处理部分的处理流程为:1)消除天线耦合。消除天线阵列中天线对间的耦合效应。2)带通滤波。压制高频和低频噪音。3)反傅里叶变换(IFFT)。将频域数据转换为时间域数据, 获得时间域数集。4)道均衡。通过道均衡处理调节由于电磁波在各对天线之间发射接收的距离, 导致数据集中各道能量不均衡。5)动校正。将各道数据转化为自激自收的零偏移距数据。6)叠加。将每一个道集的数据进行叠加, 形成叠后数据体, 提高信噪比。
实验天线采用自主研发的多次覆盖极化天线阵列, 目标体分别为金属平面板和金属二面体, 天线测量方式有共极化方式和交叉极化方式。矢量网络分析仪发射信号的扫描频带范围为:0.8 ~4.0 GHz, 扫描点数为512, 每条测线有测点N=50, 中频带宽为100 kHz, 发射平均功率为5 dBm。
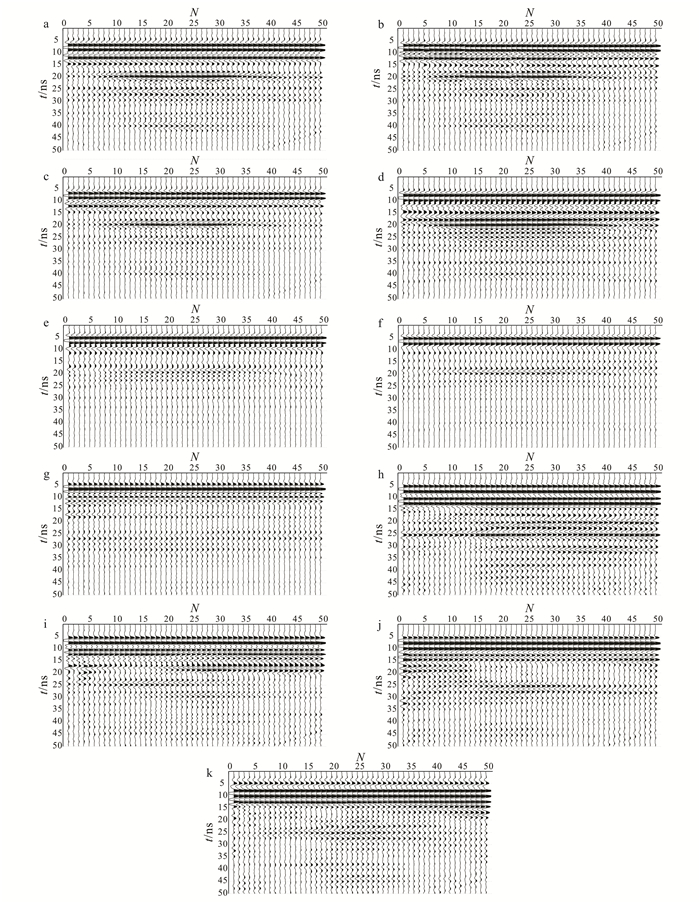
将金属平面板作为目标体的剖面图见图 6, 将金属二面体作为目标体的剖面图见图 7。
|
| a.H1发射H6接收; b.H3发射H4接收; c.HH极化模式叠加; d.V1发射V4接收; e.V2发射V3接收; f.VV极化模式叠加; g.H1发射V4接收; h.H3发射V1接收; i.H4发射V4接收; j.H6发射V1接收; k.HV极化模式叠加。 图 6 金属平面板为目标体的剖面图 Figure 6 Vertical profile of a metallic plate as the target |
|
|
|
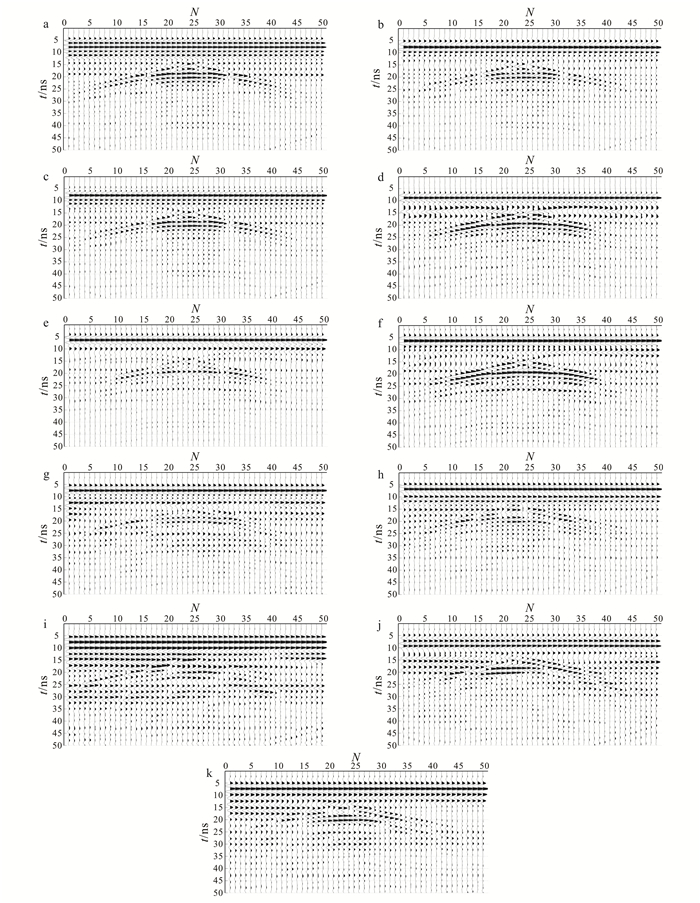
| a.H1发射H6接收; b.H3发射H4接收; c.HH极化模式叠加; d.V1发射V4接收; e.V2发射V3接收; f.VV极化模式叠加; g.H1发射V4接收; h.H3发射V1接收; i.H4发射V4接收; j.H6发射V1接收; k.HV极化模式叠加。 图 7 金属二面体为目标体的剖面图 Figure 7 Vertical profile of a metallic dihedral as the target |
|
|
雷达信号在传输过程中不可避免会受到噪声的影响, 主要为系统内部产生的带电粒子不规则扰动所产生的随机噪声, 该噪声的特点是在所有频带内均存在连续不规则的起伏变化。
由两组不同目标体的实验结果可以看出, HH极化模式有2个叠加道, VV极化模式有2个叠加道, HV极化模式有4个叠加道, 其叠加后显示的剖面图有效压制了噪声, 达到了提高信噪比的目的。
为了进一步量化对比数据叠加前后的效果, 计算叠加前后数据的信噪比:
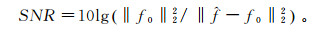
其中: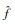
对叠加道结果进行Pauli极化分解, 其中每个Pauli基矩阵对应着一种基本的散射机制, 表示形式[11]为
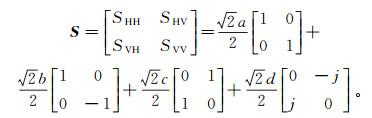
S为辛克莱散射矩阵, 系数a、b、c和d的值为
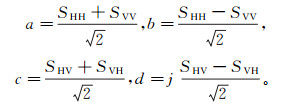
对应的4种散射机制为:第1种为平面单次或奇次散射; 第2种和第3种分别为0°和45°的二次或偶次反射; 第4种为不对称分量。
在满足单站互易定理的条件下, 即SHV=SVH, 则d=0, 此时Pauli基可简化为3个基矩阵, 总功率为
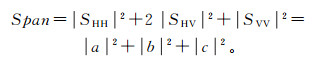
将Pauli分解得到的|a|2,|b|2和|c|2对应RGB伪彩色图像, 红色=|b|2, 绿色=|c|2, 蓝色=|a|2, 得到金属平面板及金属二面体的伪彩色图像(图 8)。

|
| a.金属平面板b.金属二面体。 图 8 Pauli极化分解伪彩色图像 Figure 8 RGB image of Pauli polarmetric decomposition |
|
|
从图 8可以看出:平面板显示为蓝色, 对应第一种散射机制为单次散射; 二面体显示为红色, 对应第二种散射机制为二次或偶次散射。
5 结论1) 在实验室应用自主研发的多输入多输出步进频率探地雷达系统和多次覆盖极化天线阵列, 对金属平面板和金属二面体进行极化信息数据采集, 经数据处理得到响应剖面图, 说明该系统可较精确地完成电磁波测量实验, 为验证理论结果提供良好的实验平台。
2) 通过对两种典型目标体的探测实验可以看出, 用多次覆盖极化天线阵列采集到的共中心点(CMP)数据, 通过叠加CMP数据来压制噪音, 有效达到提高系统测量信噪比的目的。
3) 通过应用Pauli极化分解方法可以分类典型模型, 得到目标体的伪彩色合成图。
| [1] | Robinson L A, Weir W B, Young L. Location and Recognition of Discontinuities in Dielectric Media Using Synthetic RF Pulses[J]. Proceedings of the IEEE, 1974, 62(1): 36-44. |
| [2] | Lizuka K, Fregndorfer A P, Wu K H, et al. Step-Frequency Radar[J]. Journal of Applied Physics, 1984, 56: 2572-2583. DOI:10.1063/1.334286 |
| [3] |
方广有, 佐藤源之. 频率步进探地雷达及其在地雷探测中的应用[J].
电子学报, 2005, 33(3): 436-439.
Fang Guangyou, Motoyuki Sato. Stepped-Frequency Ground Penetrating Radar and Its Application for Landmine Detection[J]. Acta Electronica Sinica, 2005, 33(3): 436-439. |
| [4] |
屈乐乐, 方广有, 杨天虹. 频率步进探地雷达系统小型化的设计与实现[J].
仪器仪表学报, 2010(3): 699-703.
Qu Lele, Fang Guangyou, Yang Tianhong. Design and Implementation of Miniature Stepped-Frequency Ground Penetrating Radar System[J]. Chinese Journal of Scientific Instrument, 2010(3): 699-703. |
| [5] | Feng Xuan, Motoyuki Sato. Pre-Stack Migration App-lied to GPR for Landmine Detection[J]. Inverse Problems, 2004, 20: S99-S115. DOI:10.1088/0266-5611/20/6/S07 |
| [6] | Bashforth M B, Lewallen T S, Nammath S R, et al. Stepped Frequency Ground Penetrating Radar: U. S. Patent 5, 325, 095[P]. 1994-06-28. |
| [7] |
习建军, 曾昭发, 黄龄, 等. 阵列式探地雷达信号极化场特征[J].
吉林大学学报(地球科学版), 2017, 47(2): 633-644.
Xi Jianjun, Zeng Zhaofa, Huang Ling, et al. Characteristics of the Signal Polarization Field in Array Type Ground Penetrating Rada[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(2): 633-644. |
| [8] |
王宪楠, 刘四新, 程浩. Shearlet变换在GPR数据随机噪声压制中的应用[J].
吉林大学学报(地球科学版), 2017, 47(6): 1855-1864.
Wang Xiannan, Liu Sixin, Cheng Hao. Application of Shearlet Transform for Suppressing Random Noise in GPR Data[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(6): 1855-1864. |
| [9] | Feng Xuan, Yu Yue, Liu Cai, et al. Subsurface Polarimetric Migration Imaging for Full Polarimetric Ground-Penetrating Radar[J]. Geophysical Journal International, 2015, 202(2): 1324-1338. DOI:10.1093/gji/ggv208 |
| [10] | Feng Xuan, Yu Yue, Liu Cai, et al. Combination of H-Alpha Decomposition and Migration for Enhancing Subsurface Target Classification of GPR[J]. IEEE Transactions on Geosciences and Remote Sensing, September, 2015, 53: 4852-4861. DOI:10.1109/TGRS.2015.2411572 |
| [11] | Lee J S, Pottier E. Polarimetric Radar Imaging:From Basics to Applications[M]. Florida: CRC Press Inc, 2009: 35-37. |


