2. 国土资源部应用地球物理重点实验室, 长春 130026;
3. 河北地质大学信息工程学院, 石家庄 050031
2. Key Laboratory of Applied Geophysics, Ministry of Land and Resources of PRC, Changchun 130026, China;
3. College of Information Engineering, Hebei GEO University, Shijiazhuang 050031, China
0 引言
航空电磁法(airborne electromagnetic method)因其不受地形影响、测量面积大等优点而广泛应用于复杂地区的矿产勘查、地质填图、地下水勘查及环境检测等领域。1984年Stanmac和McPhar公司在加拿大成功实现了固定翼飞机AEM系统的首次飞行, 标志着AEM的诞生, 之后航空电磁法测量平台和系统配置不断创新和发展[1]。我国于20世纪60年代初开始研制长导线式航空电磁系统, 之后又陆续研制了双频和三频硬架式航电仪[2]。随着航空电磁技术的发展, 航空电磁正演计算方法一直是理论研究的重要内容。Newman等[3]应用交错有限差分(FD)分别进行了二维和三维带地形的三维航空电磁响应。朱凯光等[4]开展了一维层状模型航空电磁法正演模拟, 同时研究了航空电磁响应的影响因素和一定条件下有效探测深度。高亮等[5]运用Impulse系统(频率域吊舱式直升机航空电磁测量系统)对频率域航空电磁系统进行了磁性条件下频率域航空电磁正演研究。李小康[6]基于MPI(message passing interface, 用于并行计算的通信协议)运用有限元法并行计算了2.5维频率域航空响应。曲昕馨[7]基于有限差分法实现了三维频率域航空电磁法正演模拟, 同时分析了线圈姿态对结果的影响并给出了校正方案。王卫平等[8]在实现二维和三维航空电磁正演模拟的基础上研究了地形影响, 并使用地形校正法对典型地形地电模型进行校正。殷长春等[9]运用非结构化网格的有限元法进行了2.5维航空电磁正演模拟, 分析总结了典型地形对航空响应的影响及其特征。黄威等[10]利用三维矢量有限元正演模拟研究了覆盖层和垂直接触带等典型地电构造对航空电磁响应的影响特征。Li等[11]运用等参有限元法进行了三维源/二维地电模型(2.5维)的频率域航空电磁法正反演算法研究。
由于航空电磁方法探测环境复杂, 地下介质的各向异性特征越来越受到重视。Yin等[12-13]开发了用于计算层状大地任意各向异性中直流电场和磁场的算法; 处理了任意各向异性介质中正演问题。Avdeev等[14]研究了各向异性对航空电磁测量的影响, 但其研究结果只适用于三维简单各向异性地质模型。Yin等[15-16]研究各向异性介质对于一维介质模型的影响; 考虑了各向异性对机载电磁系统响应的影响, 并分析了实测航空电磁数据的各向异性主轴方向。Liu等[17]运用有限差分法进行了任意三维各向异性模型的航空电磁响应计算, 取得了较好的应用效果。Yin等[18]进行了起伏地形任意各向异性模型下的三维时域航空电磁响应正演计算。Huang等[19]采用谱元法对航空电磁各向异性响应进行三维正演模拟, 得出了不同各向异性异常体的电磁响应的收敛条件及其识别方式。上述研究中, 各向异性介质电磁模拟研究主要以有限差分为主, 对于地下复杂结构模拟难以达到满意的模拟精度。本文采用矢量有限元法开展三维任意各向异性介质频率域航空电磁响应模拟算法, 利用矢量有限元法求解散射电场耦合方程, 通过将总场分解为一次场(背景场)和二次场(散射场)来进行各向异性介质中的频率域三维航空电磁正演模拟。针对三维模型计算量大的问题, 本文采用共享内存直接求解器PARDISO对大规模稀疏矩阵并行计算, 大大提高了计算效率。
1 正演理论假设时谐因子为eiωt, 其中, 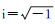
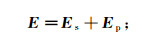 (1)
(1) 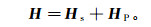 (2)
(2) 式中:E为电场强度; H为磁场强度; 下标p和s分别代表一次场和二次场。为了在保证精度的同时能提高计算效率, 本文以空气为介质的均匀全空间为背景对一次场采用解析式计算, 采用的源为垂直磁偶极源(对应水平共面装置, 简称HCP), 引入谢坤诺夫矢量势F, 通过解偏微分方程可得矢量势F表达式:
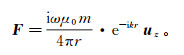 (3)
(3) 式中:m为磁距; r为计算坐标点到源点的距离, r=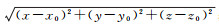
由此得到一次场电场和磁场的表达式:
 (4)
(4) 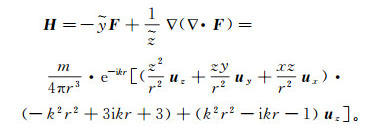 (5)
(5) 式中:x、y、z为所计算点的坐标值; ux、uy分别为x、y方向的单位向量; 

对于二次场的计算, 下式为正演模拟中二次场形式下的麦克斯韦方程组:
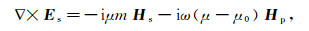 (6)
(6)  (7)
(7) (6)式和(7)式中:Js=[(σ-σp)+iω(ε-εp)]Ep, 为等效场源项, σp为背景电导率。在各向异性介质中, σ及σp用一个3×3的张量矩阵表示[20]。为实现任意各向异性电导率介质模型, 利用欧拉旋转从主轴坐标系转换到模拟坐标系, 主轴电导率张量用如下形式表示:
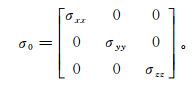 (8)
(8) 其下标x、y和z为笛卡尔坐标系的方向。欧拉旋转计算过程如下:
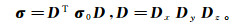 (9)
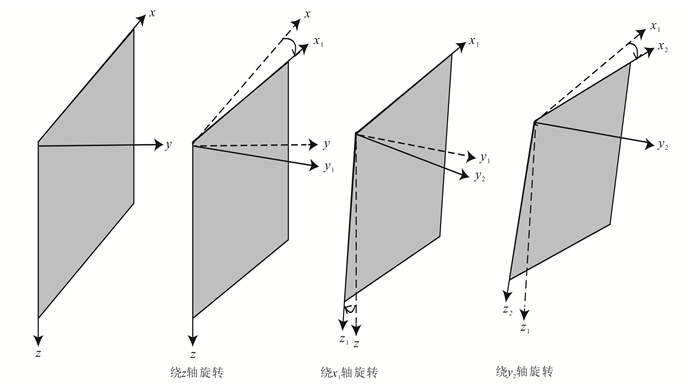
(9) 式中:D为主旋转矩阵; Dx、Dy、Dz分别是绕着x轴、y轴和z轴旋的对应矩阵(图 1), φ、ψ、χ分别为绕着x轴、y轴、z轴旋转的角度, 即
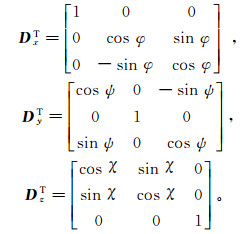 (10)
(10)
|
| 图 1 坐标旋转示意图 Figure 1 Coordinate rotation diagram |
|
|
最后得到如下形式的任意各向异性介质中的电导率张量, 该张量具有对称和正定性质[21]:
 (11)
(11) 假定磁导率为真空中的磁导率μ0, 不考虑存在位移电流的情况, 对式(6)两边同时取旋度, 将(7)式代入得到二次电场的双旋度方程:
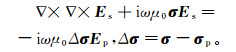 (12)
(12) 采用矢量有限元法, 用六面网格将模型剖分, 并将模拟区域离散成Ne个单元, 对式(12)采用伽辽金加权余量法可得:
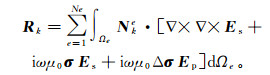 (13)
(13) 式中:Rk为单元的残数加权积分之和; Nke为第e个单元k棱边的插值函数; Ωe为单元体积。
由于模拟区域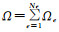
 (14)
(14) 式中, ns为面外法线单位向量。
使用狄利克雷边界条件, n为边界上的法向量, 即假设在远离异常体的边界处二次异常场衰减为0, 棱边元赋值为0, 该条件使得电磁场呈指数衰减, 从而边界处不产生反射并远离异常区[22]:
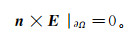 (15)
(15) 根据物性变化界面处电磁场切向连续性及所选用边界条件, 式(14)的第二项可以忽略, 改写成:
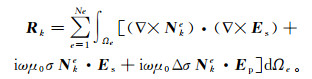 (16)
(16) 根据矢量有限元法, 即将自由度赋于棱边而不是单元节点, 可得到任意单元内场的展开式:
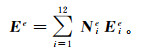 (17)
(17) 式中, Nie和Eie分别为第e个六面体单元第i条棱边的矢量基函数和切向电场值。通过xyz坐标系和ξηζ坐标系转换(图 2), 各棱边矢量基函数如下:
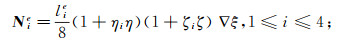 (18)
(18)  (19)
(19) 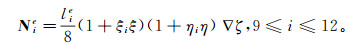 (20)
(20) 式中, lie为该六面体单元第i条棱的边长。
Es=[Ee], 将式(17)代入式(16)得:
 (21)
(21) Ke和Me即为单元刚度矩阵, 具体如下:
 (22)
(22) 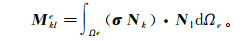 (23)
(23) 式中:k=1, …, 12;l=1, …, 12。之后, 引入雅克行列式将函数转换为以ξ、η和ζ表示的函数, 则式(22)和(23)转化为
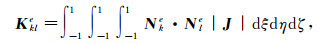 (24)
(24)  (25)
(25) 将单元刚度矩阵Me和Ke按式(22)进行全局刚度矩阵合成, 可以得到大型线性方程组:
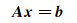 (26)
(26) 式中:A为稀疏复对称系数矩阵; x为带求解的场值; b为源端项。引入PARDISO求解器, 运用其内嵌套分割并行算法对方程共享内存并行直接求解。求解出电场值后, 磁场值可根据法拉第定律求得:
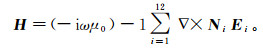 (27)
(27) 本文借鉴Liu等[17]的三维各向异性模型进行精度验证。三层介质模型如图 3所示, 其中各向异性低阻层厚度为100 m, 取主轴电导率元素为σxx=1 S/m、σyy=10 S/m、σzz=1 S/m, 并令主电导率张量绕y轴旋转45°, 上方为空气层, 下方为σ=0.01 S/m的各向同性介质高阻均匀半空间。采用水平磁偶极子源, 接收线圈和发射线圈均离地表 20 m, 发射频率为900 Hz。三维有限元计算结果与一维拟解析解结果对比如图 4所示。由图 4可见, 一维解析解和本文三维矢量有限元模拟结果能很好地吻合, 说明了本文算法的可靠性。

|
| 图 3 精度验证模型 Figure 3 Precision verification model |
|
|

|
| 图 4 验证结果 Figure 4 Validation results |
|
|
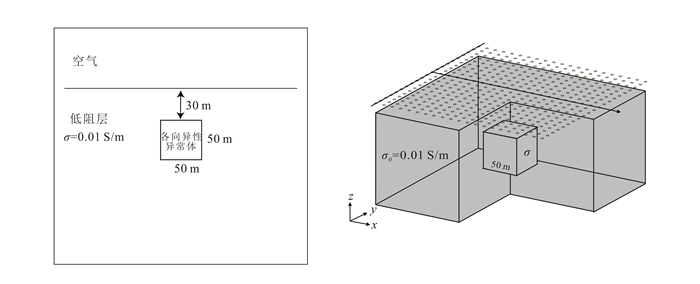
为了进一步分析不同电阻率各向异性特征对航空电磁响应的影响, 建立如图 5所示的三维地电模型。该模型为一个高导异常体埋藏在均匀半空间中, 模型大小为1 540 m×1 540 m×1 540 m, 异常体大小为50 m×50 m×50 m, 异常体中心位于坐标系原点, 埋深为30 m, 三维模型剖分为42×42×46个单元, 包含扩边区域和目标区域。其中, 扩边区单元为呈2倍扩展的渐变粗网格, 目标区域为均匀细网格。同时, 针对空中场的(空间)衰减较地中有耗衰减得慢的问题, 对于空气层的扩边多, 地下区域扩边相对少, 尽可能减少截断边界对模拟区域的影响, 从而在保证了计算精度的同时提高计算速度。长源发射频率为900 Hz, 记录磁场Hz分量, 发射线圈和接收线圈距离为10 m, 离地面20 m, 点距为10 m, 每条测线共计21个测点。
|
| 图 5 三维地电模型与测线分布 Figure 5 Three dimensional model and survey line distribution |
|
|
首先, 当各向异性异常体的主电导率张量绕不同主轴旋转后, 得到倾斜各向异性电导率张量, 设各向异性异常体主电导率参量为
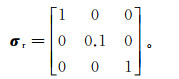 (28)
(28) 然后分别讨论以下不同各向异性情况对航空电磁响应影响规律:1)将(28)式的主电导率参量分别绕着x、z轴旋转0°、45°和90°, 分别研究磁场垂直分量的实部和虚部电磁响应特征; 2)各向异性围岩电阻率变化响应特征。
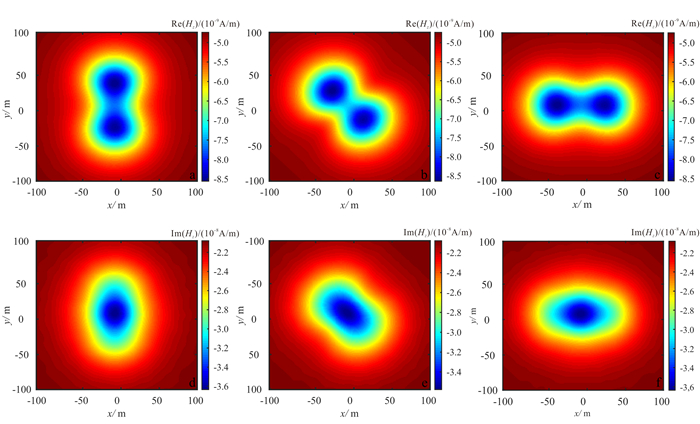
2.2.1 绕z轴旋转各向异性磁场响应特征当异常体主电导率绕z主轴旋转0°、45°、90°时, 相当于目标体从各向异性介质变为倾斜各向异性介质的过程。图 6为上述电导率张量绕z轴旋转不同角度后得到的磁场Hz分量在xy面的响应特征。由于垂直磁偶极子所产生的电流在地层内主要沿xy面流动, 因此磁场响应Hz分量沿着电导率的旋转角度旋转, 场的分布形态和主轴的方位对应良好, 可用场值的形态判断出主轴方位。根据磁场特征, 可以确定异常体的各向异性主方向以及主电导率张量旋转角度。
|
| a.各向异性异常体绕z轴旋转0°Hz分量实部; b.各向异性异常体绕z轴旋转45°Hz分量实部; c.各向异性异常体绕z轴旋转90°Hz分量实部; d.各向异性异常体绕z轴旋转0°Hz分量虚部; e.各向异性异常体绕z轴旋转45°Hz分量虚部; f.各向异性异常体绕z轴旋转90°Hz分量虚部。 图 6 各向异性异常体绕z轴旋转HCP装置磁场Hz分量响应 Figure 6 Hz component of the magnetic response of the HCP device when the anisotropic body rotates around the z axis |
|
|
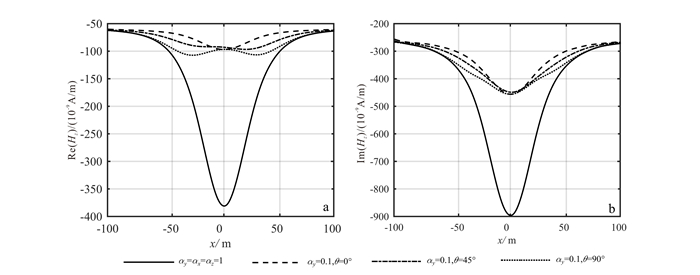
图 7所示为绕z轴旋转HCP装置Hz分量观测记录结果。对比图中实虚分量各向同性(黑实线)与不同旋转角度各向异性(黑虚线)在信号响应振幅上有较大的差异, 可见各向异性参数对航空电磁观测结果影响很大。由各向同性变为各向异性条件下, 实分量响应信号由单峰值信号逐渐变为双峰值信号, 并且信号振幅有较大幅度的衰减(图 7a)。Hz虚分量相对影响较小, 信号相位没有明显变化(图 7b)。
|
| a.各向同性异常体及各向异性异常体绕z轴旋转不同角度Hz分量实部对比; b.各向同性异常体及各向异性异常体绕z轴旋转不同角度Hz分量虚部对比。 图 7 各向异性异常体绕z轴旋转HCP装置观测记录Hz分量 Figure 7 Hz component that is recorded by an observation of the HCP device when an anisotropic anomalous body rotates around the z axis |
|
|
当各向异性电性参数沿着x轴分别旋转0°、45°和90°。HCP装置磁场Hz分量响应如图 8所示。随着旋转角度的变化, HCP装置Hz分量的实部随着旋转角度达到90°时, 磁场分量响应从双峰异常变成了关于x轴对称的单峰异常, 而虚部变化异常较小。同理, 当沿y轴旋转时, HCP装置Hz分量的实部随着旋转角度的变化从单峰异常变成关于y轴对称的单峰异常。

|
| a.各向异性异常体绕x轴旋转0°Hz分量实部; b.各向异性异常体绕x轴旋转45°Hz分量实部; c.各向异性异常体绕x轴旋转90°Hz分量实部; d.各向异性异常体绕x轴旋转0°Hz分量虚部; e.各向异性异常体绕x轴旋转45°Hz分量虚部; f.各向异性异常体绕x轴旋转90°Hz分量虚部。 图 8 各向异性异常体绕x轴旋转HCP装置磁场Hz分量响应 Figure 8 Hz component of the magnetic response of the HCP device when the anisotropic body rotates around the x axis |
|
|
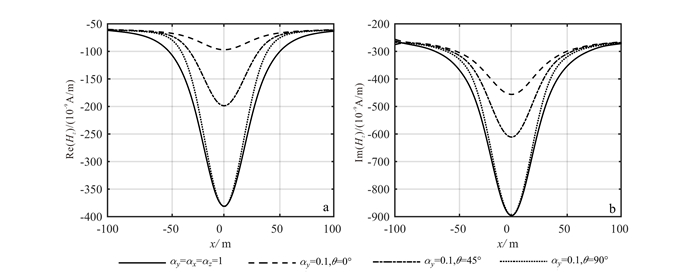
图 9所示为绕x轴旋转HCP装置Hz分量观测记录结果。与上述绕z轴旋转结果类似, 实虚分量各向同性(黑实线)与不同旋转角度各向异性(黑虚线)在信号响应振幅上有较大的差异, 实分量在不同旋转角度情况下, 响应信号振幅影响更大, 在目标位置响应信号振幅随着旋转角度的变化, 振幅峰值由-400×10-9 A/m(旋转90°)转变为-100×10-9 A/m(旋转0°)。相比而言, 虚分量幅值变化率相对较小。
|
| a.各向同性异常体及各向异性异常体绕x轴旋转不同角度Hz分量实部对比; b.各向同性异常体及各向异性异常体绕x轴旋转不同角度Hz分量虚部对比。 图 9 各向异性异常体绕x轴旋转HCP装置观测记录Hz分量 Figure 9 Hz component that is recorded by an observation of the HCP device when an anisotropic anomalous body rotates around the x axis |
|
|
当地下介质呈交替分布时, 围岩电性参数呈各向异性特征。在上述模型(图 5)的基础上改变围岩电性参数各向异性特征, 使围岩沿y方向电导率增大, 围岩主电导率张量为
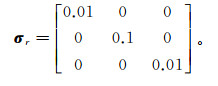 (29)
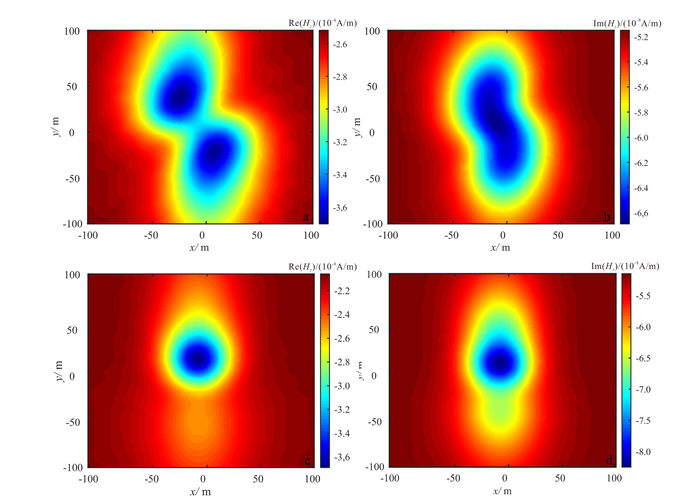
(29) 同时, 各向异性异常体的主电导率张量分别绕z、x轴旋转45°, 计算得到异常体在各向异性围岩内的电磁响应(图 10)。对比图 6和图 8围岩为各向同性旋转相同角度的磁场Hz分量响应图可见, 围岩各向异性对磁场响应影响较大, 特别是在目标信号能量分布上产生较大变化, 由对称的双峰或单峰结构变为不规则的能量团分布。当围岩沿y轴电导率增大则在该方向呈良导性质, 而相应的x轴方向呈高阻性质, 由于电磁波在良导和高阻的情况下有不同的衰减速度, 因此可以看出磁场Hz分量平面分布沿着y方向延展。
|
| a.各向异性围岩-绕z轴旋转各向异性异常体Hz分量实部; b.各向异性围岩-绕z轴旋转各向异性异常体Hz分量虚部; c.各向异性围岩-绕x轴旋转各向异性异常体Hz分量实部; d.各向异性围岩-绕x轴旋转各向异异常体性Hz分量虚部。 图 10 在主轴电导率不同的围岩下各向异性异常体绕z、x轴旋转磁场响应Hz分量 Figure 10 Hz component of the magnetic field response of an anisotropic anomalous body rotating around z and x axes under different conductivities of surrounding rock |
|
|
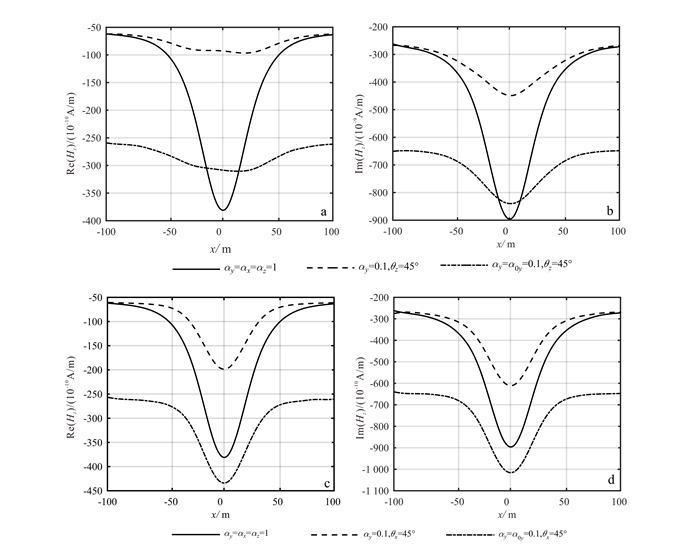
图 11所示为HCP装置记录所得Hz响应曲线。图中黑实线为常规各向同性记录结果, 黑虚线为异常体各向异性旋转45°结果, 黑点划线为背景介质同时为各向异性记录结果。由图 11实虚分量绕x、z轴的旋转HCP装置Hz分量记录结果可见, 当背景介质存在各向异性特征时, 记录信号在形状上与背景各向同性-目标各向异性类似, 但在信号振幅值上有较大的差异, 与完全各向同性相比, 目标响应信号较弱, 说明各向异性造成目标体的识别能力降低。
|
| a.全各向同性模型至全各向异性模型(异常体绕z轴旋转)Hz分量实部曲线; b.全各向同性模型至全各向异性模型(异常体绕z轴旋转)Hz分量虚部曲线; c.全各向同性模型至全各向异性模型(异常体绕x轴旋转)Hz分量实部曲线; d.全各向同性模型至全各向异性模型(异常体绕x轴旋转)Hz分量虚部曲线。 图 11 在主轴电导率不同的围岩下各向异性异常体HCP装置Hz分量记录结果 Figure 11 Hz component of an anisotropic abnormal body HCP device under different conductivity of surrounding rock |
|
|
本文基于矢量有限元法并通过分离总场提出了任意各向异性情况下三维频率域航空电磁正演模拟算法, 通过典型的理论模型与一维解析解对比, 验证了该算法的精度和有效性。针对典型的各向异性电阻率模型, 分别计算得到了不同参数条件下的磁场响应特征并总结得出以下规律:
1) 磁场分布和主电导率张量的旋转方向之间有很强的相关性, 为识别各向异性异常体的主轴方向和主轴电导率提供依据, 根据这些性质可以进一步识别异常体的层理性质, 即其走向和倾角。
2) 当围岩呈各向异性时, 由于各向异性介质中的通道效应, 即电流会沿呈导电性质的方向聚焦, 磁场响应会随之改变, 记录信号相比于各向同性介质在响应振幅和相位上都有较大的变化, 且异常体响应信号变弱。
3) 航空电磁响应受到各向异性介质影响较大, 但其也有明显的特征, 根据其分布可以判断各向异性异常体的电性情况与层理方向, 同时也能判断围岩的电性情况。本文的计算结果和各向异性影响特征为实际解释航空电磁响应结果提供了依据。同时各向异性正演算法也为进一步开展航空电磁各向异性反演提供了基础。
| [1] |
雷栋, 胡祥云, 张素芳. 航空电磁法的发展现状[J].
地质找矿论丛, 2006, 21(1): 40-44, 53.
Lei Dong, Hu Xiangyun, Zhang Sufang. Development of Airborne Electromagnetic Method[J]. Contributions to Geology and Mineral Resources Research, 2006, 21(1): 40-44, 53. |
| [2] |
王卫平. 频率域航空电磁法发展研究现状与应用研究[C]//中国地球物理学会. 中国地球物理学会第二十七届年会论文集. 北京: 中国地球物理学会, 2011: 2.
Wang Weiping. Application and Prospect of the Research About Frequeney Domain Airborne Electromagneite Method[C]//Chinese Geophysical Society. Proceedings of the Twenty-Seventh Annual Meeting of China Geophysical Society. Beijing: China Geophysical Society, 2011: 2. |
| [3] | Newman G A, Alumbaugh D L. Frequency Domain Modeling of Airborne Electromagnetic Responses Using Staggered Finite Differences[J]. Geophysical Prospecting, 1995, 43: 1021-1042. DOI:10.1111/gpr.1995.43.issue-8 |
| [4] |
朱凯光, 林君, 刘长胜, 等. 频率域航空电磁法一维正演与探测深度[J].
地球物理学进展, 2008, 23(6): 1943-1946.
Zhu Kaiguang, Lin Jun, Liu Changsheng, et al. One-dimensional Forwand and Prospecting Depth for Airborne Frequency Domain Electromagnetic Method[J]. Progress in Geophysics, 2008, 23(6): 1943-1946. |
| [5] |
高亮, 胡祥云, 王卫平, 等. 磁性条件下频率域航空电磁法正演研究[J].
工程地球物理学报, 2009, 6(4): 399-403.
Gao Liang, Hu Xiangyun, Wang Weiping, et al. A Study of Frequency Airborne Electromagnetic Forward Under Magnetic Condition[J]. Chinese Journal of Engineering Geophysics, 2009, 6(4): 399-403. |
| [6] |
李小康. 基于MPI的频率域航空电磁法有限元二维正演并行计算研究[D]. 北京: 中国地质大学, 2011.
Li Xiaokang. A MPI Based Parallel Calculation Investigation on Two Dimensional Finite Element Modelling of AEM[D]. Beijing: China University of Geosciences, 2011. http://cdmd.cnki.com.cn/Article/CDMD-11415-1011077505.htm |
| [7] |
曲昕馨. 三维频率域航空电磁法的数值模拟及姿态影响和校正研究[D]. 长春: 吉林大学, 2014.
Qu Xinxin. Numerical Simulation Attitude Effect and Correction of 3-D Frequency Domain Helicopterborne Electromagnetic Method[D]. Changchun: Jilin University, 2014. |
| [8] |
王卫平, 曾昭发, 李静, 等. 频率域航空电磁法地形影响和校正方法[J].
吉林大学学报(地球科学版), 2015, 45(3): 941-951.
Wang Weiping, Zeng Zhaofa, Li Jing, et al. Topographic Effects and Correction for Frequency Airborne Electromagnetic Method[J]. Journal of Jilin University(Earth Science Edition), 2015, 45(3): 941-951. |
| [9] |
殷长春, 张博, 刘云鹤, 等. 2.5维起伏地表条件下时间域航空电磁正演模拟[J].
地球物理学报, 2015, 58(4): 1411-1424.
Yin Changchun, Zhang Bo, Liu Yunhe, et al. 2.5-D Forward Modeling of the Time-Domain Airborne EM Aystem in Areas with Topographic Relie[J]. Chinese Journal of Geophysics, 2015, 58(4): 1411-1424. DOI:10.6038/cjg20150427 |
| [10] |
黄威, 殷长春, 贲放, 等. 频率域航空电磁三维矢量有限元正演模拟[J].
地球科学, 2016, 41(2): 341-342.
Huang Wei, Yin Changchun, Ben Fang, et al. 3D Forward Modelling for Frequency AEM by Vector Finite-Element[J]. Earth Science, 2016, 41(2): 341-342. DOI:10.11764/j.issn.16721926.2016.02.0341 |
| [11] | Li Wenben, Zeng Zhaofa, Li Jing, et al. 2.5D Fo-rward Modeling and In-Version of Frequency-Domain Airborne Electromagnetic Data[J]. Applied Geophysics, 2016, 13(1): 37-47, 218. |
| [12] | Yin C, Weidelt P. Geoelectrical Fields in a Layered Earth with Arbitrary Anisotropy[J]. Geophysics, 1999, 64(2): 426-434. DOI:10.1190/1.1444547 |
| [13] | Yin C, Maurer, H .M. Electromagnetic Induction in a Layered Earth with Arbitrary Anisotropy[J]. Geophysics, 2001, 66(5): 1405-1416. DOI:10.1190/1.1487086 |
| [14] | Avdeev D B, Kuvshinov A V, Pankratov O V, et al. Three-Dimensional Frequency-Domain Modeling of Airborne Electromagnetic Responses[J]. Exploration Geophysics, 1998, 29(2): 111-119. DOI:10.1071/EG998111 |
| [15] | Yin C, Fraser D C. The Effect of the Electrical Ani-sotropy on the Response of Helicopter-Borne Frequency-Domain Electromagnetic Systems[J]. Geophysical Prospecting, 2004, 52(5): 399-416. DOI:10.1111/gpr.2004.52.issue-5 |
| [16] | Yin C, Hodges G. Simulated Annealing for Airborne EM Inversion[J]. Geophysics, 2007, 72(4): F189-F196. DOI:10.1190/1.2736195 |
| [17] | Liu Y, Yin C. 3D Anisotropic Modeling for Airborne EM Systems Using Finite-Difference Method[J]. Journal of Applied Geophysics, 2014, 109: 186-194. DOI:10.1016/j.jappgeo.2014.07.003 |
| [18] | Yin C, Yan F, Liu Y. 3D Time-Domain Airborne EM Modeling for an Arbitrarily Anisotropic Earth[J]. Journal of Applied Geophysics, 2016, 131: 163-178. DOI:10.1016/j.jappgeo.2016.05.013 |
| [19] | Huang X, Yin C, Cao X Y, et al. 3D Anisotropic Modeling and Identification for Airborne EM Systems Based on the Spectral-Element Method[J]. Applied Geophysics, 2017, 14(3): 419-430. DOI:10.1007/s11770-017-0632-y |
| [20] | Yin C. Geoelectrical Inversion for a One-Dimensional Anisotropic Model and Inherent Non-Uniqueness[J]. Geophys J Int, 2000, 140(1): 11-23. DOI:10.1046/j.1365-246x.2000.00974.x |
| [21] | Onsager L. Reciprocal Relations in Irreversible Pro-cesses[J]. Physical Review, 1931, 37(37): 405-426. |
| [22] | Mitsuhata Y. 2-D Electromagnetic Modeling by Finite Element Method with a DipoleSource and Top—Ography[J]. Geophysics, 2000, 65(2): 465-475. DOI:10.1190/1.1444740 |
| [23] |
金建铭.
电磁场有限元方法[M]. 西安: 西安电子科技大学出版社, 1998.
Jin Jianming. Electromagnetic Finite Element Method[M]. Xi'an: Xidian University Press, 1998. |




