0 前言
在位场数据处理过程中, 对场源进行边界识别是不可或缺的, 其实质是根据目标体边界两侧存在明显的密度及磁性差异来划分边界, 从而确定目标体的水平位置。场源边界识别方法分为数理统计方法和数值计算方法。
数理统计方法主要有小子域滤波[1]和归一化标准差法[2], 这类方法都是采用滑动窗口的方式对异常数据进行统计运算, 优点在于能够利用窗口来控制噪声, 但窗口的尺寸通常凭经验给定, 因此存在主观因素, 会影响计算结果。
数值计算方法主要包括垂向导数、总水平导数(THDR)、解析信号振幅(ASM)、倾斜角(TILT)和Theta图法。这5种方法是最基本的数值计算方法, 在此之后所提出的数值计算方法都是以这5种方法进行改进得到。Hood等[3]提出利用垂向一阶导数确定铅锤台阶边缘位置, 垂向导数是通过零值点的位置来识别边界, 该方法分辨能力强, 但易受高频干扰。Cordell[4]提出总水平导数法, 通过对重力异常求总水平导数来划分目标体边界, 但该方法极易受场源埋深影响, 不能有效识别出深部的、小的地质体的边缘位置。Nabighian[5]提出解析信号振幅法, 该方法受磁异常分量和磁化方向影响较小, 不足之处是分辨率低。上述3种方法均不能很好地均衡不同振幅异常, 尤其是振幅值存在较大差异时, 边界识别效果不理想。Miller等[6]提出第一个边界识别均衡滤波器—倾斜角法, 但用该方法进行边界识别不能突出边界的异常值, 划分边界不够准确。Theta图法由Wijins等[7]提出, 该方法能够均衡高低幅值的重磁异常数据, 但存在解析奇点。马国庆等[8]提出利用总水平导数与垂直导数的相关系数进行地质体边界的识别, 但该方法对小范围异常体的识别效果不是很好。马国庆等[9]进而提出增强型滤波器圈定边界, 得到了较好的识别效果。综上, 数值计算方法便于实现且计算速度快, 但在处理实际数据时, 求导会放大噪声, 而且识别出的地质体边界过于宽泛, 不能对边界进行精确的划分; 因此, 如何解决噪声干扰和边界收敛问题需要进一步研究。
小波变换由于具有多尺度分析的特点, 能够有效地提取目标体特征, 同时具有较强的抗噪声能力, 在数据处理中得到了广泛的应用。徐亚等[10]总结了小波变换在位场数据应用中的理论方法及发展现状, 认为小波变换可应用于位场的分离、去噪、地质体边缘提取等。
本文采用小波结合传统边界识别方法对数据进行处理, 验证小波对噪声的压制能力。针对传统方法在进行边界识别时存在的边界收敛问题, 本文提出幂次变换的方法对边界进行收敛, 并将这两种方法相结合应用于模型和实际位场数据的边界识别, 同时与传统方法识别效果进行对比分析, 证实改进的方法获得了更好的边界识别效果。
1 小波变换 1.1 离散小波变换设g(t)为母小波函数, 且g(t)∈L2(R), L(R)为平方可积实数空间, 对g(t)做伸缩和平移后得到[11]:
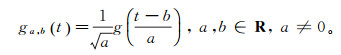 (1)
(1) 式中:t∈R; ga, b(t)为小波函数, 简称小波; a是尺度因子, 表征函数的伸缩程度; b是位置因子, 反映函数的平移位置。
对a, b进行离散化, 即:
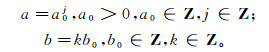
则离散小波变为
 (2)
(2) 信号s(t)∈L2(R)的离散小波变换定义为
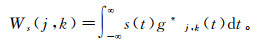
式中:g*(t)表示g(t)的复共轭。
其反变换[11]定义为
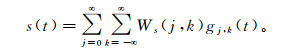 (4)
(4) 多分辨率分析是将L2(R)空间分解为不同分辨率的子空间序列, 其子空间序列的极限就是L2(R)。其中任意函数s(t)∈L2(R), s(t)投影到每一个子空间得到一系列近似函数, 这一系列近似函数逼近极限就是s(t)。通过研究各个子空间的投影, 从而可分析s(t)在不同分辨率子空间上的性质和特征[12]。
在多分辨率分析中, Vj称为尺度空间。通常, 不同的尺度空间对应尺度不同函数, 从而可用来研究总空间L2(R)的不同分辨率特征。设φ是尺度函数, 则存在系数序列h(k), k∈Z[12], 得到
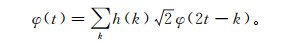 (5)
(5) 对任意的s(t)∈Vj, 首先将其分解为细节部分和近似部分, 然后再将近似部分进一步分解; 再重复以上两步, 直到得到任意尺度上的细节部分和近似部分, 这就是Mallat算法的原理。s(t)在Vj空间的展开式是
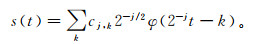 (6)
(6) 式中:k∈Z; j∈Z; cj, k为j尺度上的近似系数。
将s(t)分解一次得到
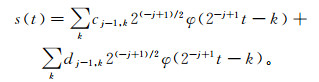 (7)
(7) 式中:dj-1, k是j-1尺度上的细节系数。将cj-1, k进一步分解下去, 可以分别得到系数cj-2, k和dj-2, k; 再继续分解, 从而达到任意空间尺度的分解系数。其重构算法表达式如下:
 (8)
(8) 其中:n∈Z; h(k)(k∈Z)相当于低通滤波器; g(k)(k∈Z)相当于高通滤波器。由式(8)可以看出, 对信号进行分解得到的近似系数, 是信号与低通滤波器作用的结果, 而细节系数是信号和高通滤波器作用得到的; 因此近似系数相对细节系数包含更多的低频信息和更少的高频信息, 从而达到压制噪声的目的。
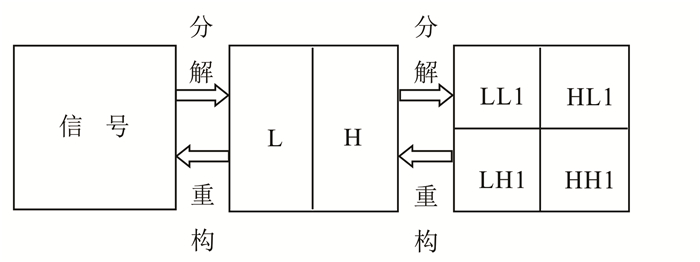
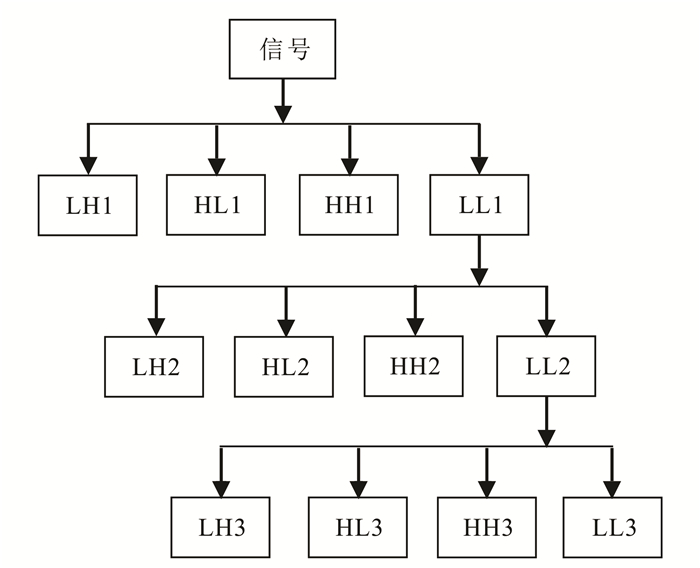
图 1给出了第一层的小波分解和重构计算过程, 首先将信号分解为低频信息L与高频信息H; 然后再将低频信息L分解为低频信息LL1与其高频信息LH1, 同时将高频信息H分解为HL1和HH1[13]。其中LL1为第一层近似系数, 其余成分为细节系数, 这就是第一层的分解过程; 第二层的分解是以LL1为原始信号重复相同的操作[14], 以此类推, 如图 2所示。
|
| 图 1 Mallat算法第一层分解重构图示 Figure 1 First layer of Mallat algorithm decomposition and reconstruction |
|
|
|
| 图 2 Mallat算法塔式分解示意图 Figure 2 Sketch map of Mallat algorithm pyramid decomposition |
|
|
当对所分解的小尺度上的系数进行重构时, 我们只选取近似系数, 这样可以有效压制噪声。层数越高, 对噪声的压制作用越明显, 但会丢失细节信息, 导致边界识别结果发散; 因此, 本文选取小波变换的第一层和第二层近似系数进行重构来验证试验效果。
2 幂次变换原理针对传统边界识别方法在处理数据时边界不够收敛、识别效果不理想的问题, 本文提出幂次变换的方法来提高收敛。该方法实质上是在传统数值计算方法上加以改进, 提高整体计算的幂级数。本文选取了总水平导数、倾斜角和Theta图这3种边界识别中应用广泛且效果较好的数值计算方法进行幂次变换, 并与原方法的识别效果进行对比, 验证收敛效果。
2.1 数值计算方法总水平导数法是通过极大值来判定地质构造的边界。该方法对噪声不敏感, 但当场源埋深增大时, 识别出的边界会与实际边界位置存在较大偏差[15]。假设V表示位场异常数据, 总水平导数计算公式为
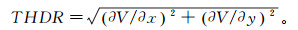 (9)
(9) 倾斜角法将垂向导数和水平导数做比值计算, 可有效克服导数计算随深度增大迅速衰减的问题。倾斜角计算公式为
 (10)
(10) 该方法受场源埋深影响较小, 可实现在场源内部为正值, 边界附近为零值, 场源外部为负值, 从而识别深部和浅部场源体的边界[16]; 但这种识别方法效果不理想, 并不能直观地显示出目标体的边缘位置。为了突出目标体的边界, 本文对倾斜角法做进一步的改进, 称其为可视化倾斜角法, 可视化倾斜角ETILT的公式为
 (11)
(11) 式中:C为常数, 通常情况下C≥2。这种方法能够提高边界的异常幅值, 降低周围的异常值, 能够更好地突出边界的位置信息。
Theta图法是求取总水平导数比上总水平导数与垂直导数之和的夹角θ的余弦, 公式为
 (12)
(12) Theta图的数值在[0, 1]范围内, 利用极大值进行场源体的边界识别, 并可增强弱异常、降低场源埋深的影响。
这几种常用的数值计算方法在边界识别中都得到了较好的结果, 同时也都存在明显的缺点, 因此本文提出幂次变换的方法加以改进。
2.2 幂次变换对以上几种数值计算方法进行幂次变换, 给出表达式, 总水平导数法为
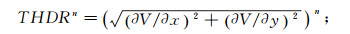 (13)
(13) 可视化倾斜角法为
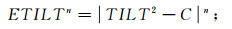 (14)
(14) Theta图法为
 (15)
(15) 式中:n表示级数(n≥1)。当n=1时, 与原数值计算方法相同。n的取值决定于原方法对地质体边界的识别能力, 根据边界识别效果择最优来选取; n越大, 对边界的收敛程度越高, 但级数过高会丢失细节信息, 通常n≤8。
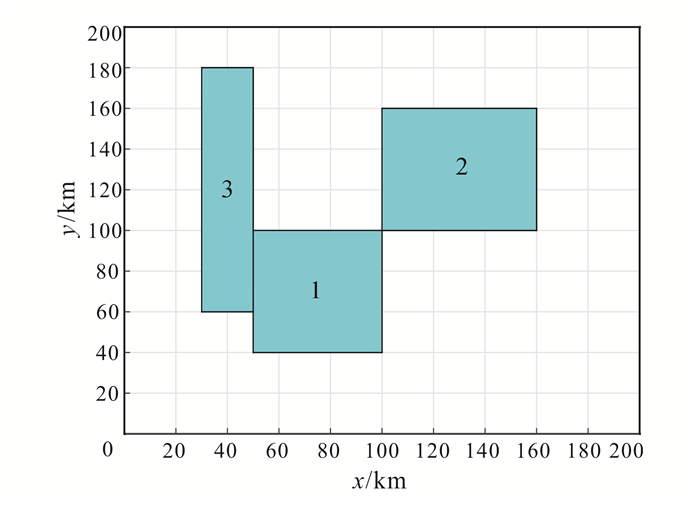
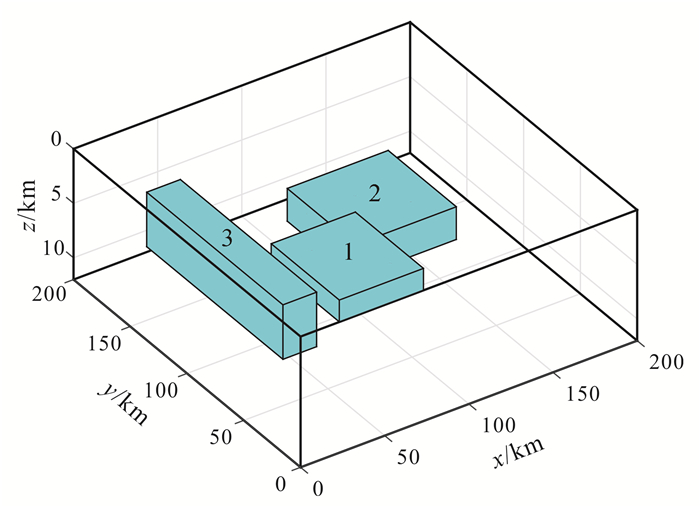
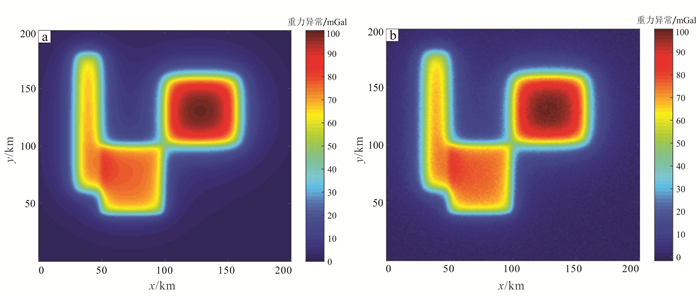
3 模型试验重力异常模型包含3个剩余密度均匀的棱柱体, 且在水平面上的投影位置没有叠加, 将棱柱体的起点(距离空间直角坐标系0点最近)坐标和尺寸(长宽高)分为2个数组, 与剩余密度一起在表 1中给出, 它们的平面分布及空间分布分别如图 3、图 4所示。计算这个模型的重力异常响应, 并在正演数据中加入随机噪声, 信噪比为35。正演数据和加噪声数据如图 5所示。
| 棱柱体 | 起点坐标 | 尺寸 | 剩余密度/(kg/m3) |
| 1 | (50, 40, 3) | 50 km×60 km×2 km | 1 000 |
| 2 | (100, 100, 6) | 60 km×60 km×3 km | 1 000 |
| 3 | (30, 60, 4) | 20 km×120 km×5 km | 500 |
|
| 图 3 重力异常模型棱柱体的平面分布 Figure 3 Planar distribution of the prisms |
|
|
|
| 图 4 重力异常模型棱柱体的空间分布 Figure 4 Spatial distribution of the prisms |
|
|
|
| 图 5 模型重力异常(a)和含有噪声的模型重力异常(b) Figure 5 Gravity anomaly of the model(a) and gravity anomaly contaminated with random noise(b) |
|
|
此模型正演数据均为正值, 在棱柱体的边界位置存在接触区域, 因此在进行边界识别时存在一定难度。添加随机噪声可以有效检验小波压制噪声的能力。将小波与幂次变换结合, 与3种传统的位场边界识别数值计算方法总水平导数、倾斜角、Theta图共同应用于模型数据。模型数据及加噪声数据小波处理后边界识别结果分别如图 6、图 7所示, 再进行幂次变换, 边界识别效果如图 8、图 9所示, 可以看出单独小波处理以及与幂次变换结合2种方法在模型数据的应用中都取得了较好的边界识别效果。

|
| a.ETILT边界识别结果; b.ETILT第一层近似系数重构边界识别结果; c.ETILT第二层近似系数重构边界识别结果; d.THDR边界识别结果; e.THDR第一层近似系数重构边界识别结果; f.THDR第二层近似系数重构边界识别结果; g.Theta图边界识别结果; h.Theta图第一层近似系数重构边界识别结果; i;Theta图第二层近似系数重构边界识别结果。其中黑色边框表示棱柱体在测量平面的水平位置投影。 图 6 模型数据小波变换边界识别结果 Figure 6 Edge detection results of wavelet transfromed model data |
|
|

|
| a.ETILT边界识别结果; b.ETILT第一层近似系数重构边界识别结果; c.ETILT第二层近似系数重构边界识别结果; d.THDR边界识别结果; e.THDR第一层近似系数重构边界识别结果; f.THDR第二层近似系数重构边界识别结果; g.Theta图边界识别结果; h.Theta图第一层近似系数重构边界识别结果; i.Theta图第二层近似系数重构边界识别结果。其中黑色边框表示棱柱体在测量平面的水平位置投影。 图 7 含噪声模型数据小波变换边界识别结果 Figure 7 Edge detection results of wavelet transfromed model data with noise |
|
|

|
| a.ETILT边界识别结果; b.ETILT第一层近似系数重构加幂次边界识别结果; c.ETILT第二层近似系数重构加幂次边界识别结果; d.THDR边界识别结果; e.THDR第一层近似系数重构加幂次边界识别结果; f.THDR第二层近似系数重构加幂次边界识别结果; g.Theta图边界识别结果; h.Theta图第一层近似系数重构加幂次边界识别结果; i.Theta图第二层近似系数重构加幂次边界识别结果。其中黑色边框表示棱柱体在测量平面的水平位置投影。 图 8 模型数据小波结合幂次变换边界识别结果 Figure 8 Edge detection results of wavelet and power transfromed model data |
|
|
|
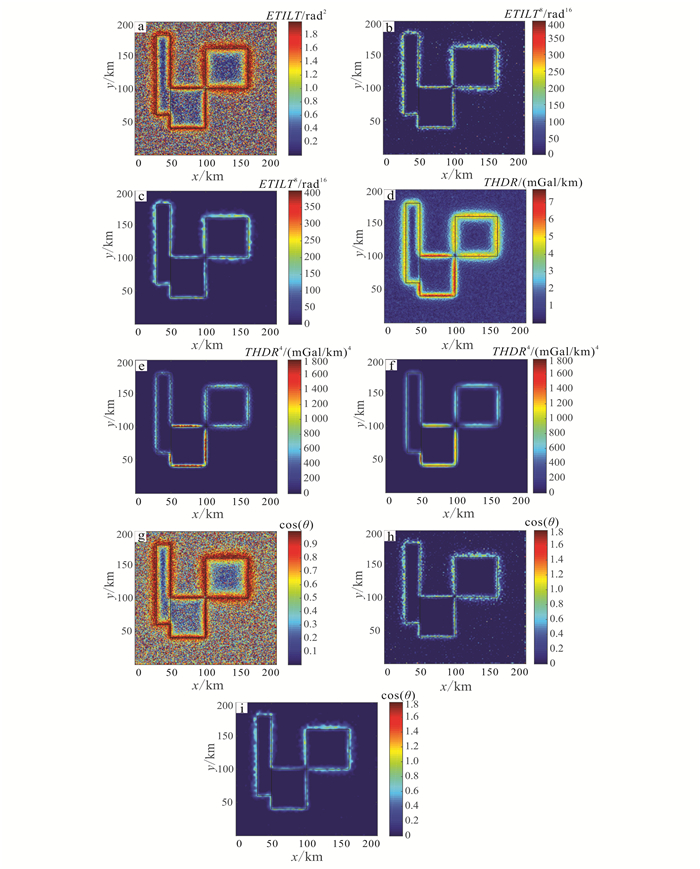
| a.ETILT边界识别结果; b.ETILT第一层近似系数重构加幂次边界识别结果; c.ETILT第二层近似系数重构加幂次边界识别结果; d.THDR边界识别结果; e.THDR第一层近似系数重构加幂次边界识别结果; f.THDR第二层近似系数重构加幂次边界识别结果; g.Theta图边界识别结果; h.Theta图第一层近似系数重构加幂次边界识别结果; i.Theta图第二层近似系数重构加幂次边界识别结果。其中黑色边框表示棱柱体在测量平面的水平位置投影。 图 9 含有噪声的模型数据小波结合幂次变换边界识别结果 Figure 9 Edge detection results of wavelet and power transfromed model data with noise |
|
|
图 6a、图 7a为可视化倾斜角法识别结果, 图 6d、图 7d为总水平导数法识别结果, 图 6g、图 7g为Theta图法识别结果。可以看出, 3种方法都基本给出了3个棱柱体真实的边界信息, 并且可视化倾斜角法的边界识别效果与Theta图法十分相似, 均为高值表示目标体边界, 能够更好地突出边缘的位置信息。图 6b和图 7b、图 6e和图 7e、图 6h和图 7h是分别在相应的数值计算方法的基础上进行小波变换, 选取第一层的近似系数进行重构得到, 图 6c和图 7c、图 6f和图 7f、图 6i和图 7i是应用小波变换第二层近似系数重构得到, 但因为图 6是基于无噪声的模型数据进行处理, 因此是否采用小波变换没有明显差别。由图 7可以看出, 通过对分解得到的近似系数进行重构可以有效地起到压制噪声的作用, 且层数越高, 压制作用越明显, 同时也会导致更多细节信息的损失。经过试验, 本文选择两层近似系数进行重构。图 8、图 9分别在图 6、图 7的基础上, 基于小波处理结果再进行幂次变换得到, 其中, 可视化倾斜角和Theta图进行了8次幂变换, 总水平导数进行了4次幂变换。将图 6与图 8进行对比, 可以看出在无噪声数据中, 幂次变换能够对目标体的边界进行有效的收敛, 使得边界划分更加清晰; 由图 7与图 9的对比可以看出, 对于含噪声的模型数据, 小波变换能够有效压制噪声, 再结合幂次变换可以达到更好的边界收敛效果, 从而进一步提高边界识别精度。
4 实际数据应用为验证本文方法在实际位场数据中的应用效果, 我们分别处理了四川盆地重力异常数据和朱日和地区的磁测数据。
首先对四川盆地布格重力异常数据进行边界识别处理, 结果见图 10, 其中图 10a为布格重力异常图。从图 10可以看出:总水平导数法对实测数据的识别效果不太理想, 仅能识别出大的断裂, 对于一些细小断裂不能清晰地显示出来(图 10e); 可视化倾斜角和Theta图的边界识别结果有一定相似性, 均可大体识别出研究区域内存在的断裂构造, 但构造分布范围较广, 未实现精确划分(图 10b、h); 在总水平导数的基础上对其进行小波变换并分别选取第一层和第二层近似系数进行重构、再进行二次幂变换后, 噪声均得到了压制, 同时识别出的断裂位置更收敛(图 10f、g); 对可视化倾斜角和Theta图做小波变换第一层近似系数重构和幂次变换的处理, 幂级数分别为3、4, 则噪声影响明显降低, 且断裂水平位置更清晰, 提高了识别精度(图 10c、i); 对可视化倾斜角和Theta图做小波变换第二层系数重构及幂次变换的处理, 且幂级数不变, 则噪声被进一步压制, 收敛程度提高, 整体效果与第一层系数重构处理结果大致相同(图 10d、j)。

|
| a.四川盆地重力异常; b.ETILT边界识别结果; c.ETILT第一层近似系数重构加幂次边界识别结果; d.ETILT第二层近似系数重构加幂次边界识别结果; e.THDR边界识别结果; f.THDR第一层近似系数重构加幂次边界识别结果; g.THDR第二层近似系数重构加幂次边界识别结果; h.Theta图边界识别结果; i.Theta图第一层近似系数重构加幂次边界识别结果; j.Theta图第二层近似系数重构加幂次边界识别结果。。 图 10 四川盆地重力异常数据边界识别结果 Figure 10 Edge detection results of gravity anomaly of Sichuan basin |
|
|
|
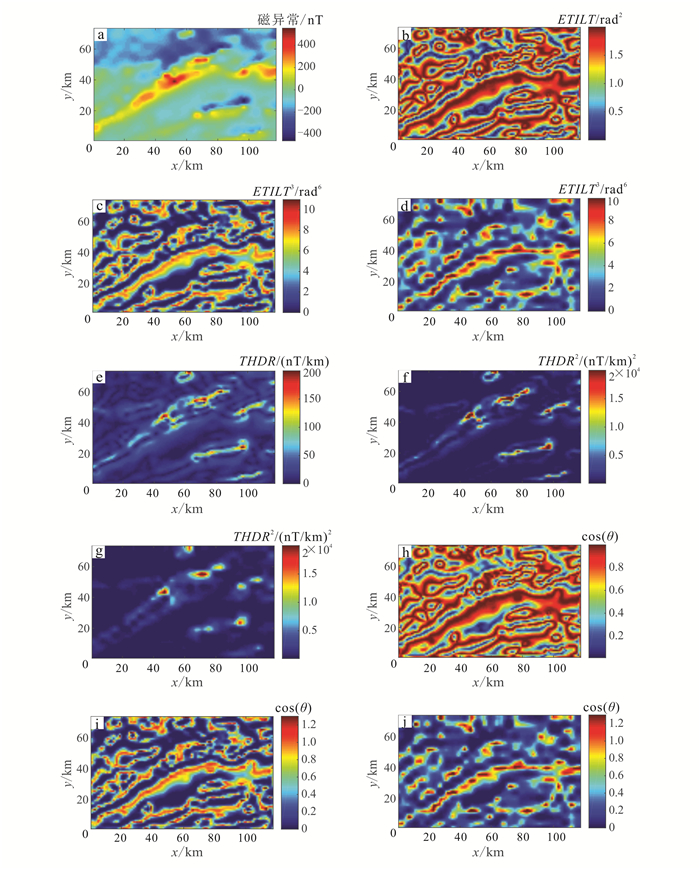
| a.经过化磁极的磁异常数据; b.ETILT边界识别结果; c.ETILT第一层近似系数重构加幂次边界识别结果; d.ETILT第二层近似系数重构加幂次边界识别结果; e.THDR边界识别结果; f.THDR第一层近似系数重构加幂次边界识别结果; g.THDR第二层近似系数重构加幂次边界识别结果; h.Theta图边界识别结果; i.Theta图第一层近似系数重构加幂次边界识别结果; j.Theta图第二层近似系数重构加幂次边界识别结果。 图 11 朱日和地区磁异常数据边界识别结果 Figure 11 Edge detection results of magnetic anomaly of Zhurihe region |
|
|
将本文方法应用于磁异常数据的边界识别, 对朱日和地区的磁数据进行化极处理得到异常如图 11所示。从图 11a可明显看出成矿带的大致范围; 从总水平导数法的识别结果(图 11e)可以看出该方法能够大致识别出断裂的水平位置, 但对断裂的边界识别效果不理想, 而且对于细小的地质构造不能清晰划分; 图 11f是在总水平导数的基础上做小波第一层近似系数重构及幂次变换的结果, 幂级数为2, 该方法能够清晰地识别出大断裂的边界位置, 识别效果较为理想; 图 11g是在总水平导数的基础上做第二层系数重构及幂次变换的结果, 幂级数也为2, 可以看出与第一层相比较, 第二层系数重构能够进一步压制噪声, 但会损失细节信息, 导致边界发散; 图 11b、h分别为可视化倾斜角法、Theta图法的识别结果, 2种方法对磁异常数据进行处理的边界识别效果相似, 都能够清晰识别出大断裂和一些细小断裂的边界, 但是边界范围不够收敛; 图 11c、i是分别对其做第一层近似系数重构结合幂次变换的处理结果, 幂级数分别为3和4, 由图看出该方法能够有效对边界进行收敛, 更加精确地划分出断裂边界的位置; 图 11d、j是采用第二层系数重构结合幂次的结果, 幂级数不变, 可见, 经第二层重构之后, 会丢失细节信息, 导致识别效果发散, 因此在处理朱日和地区磁异常数据时, 第一层系数重构结合幂次变换能够更好地划分测区内断裂构造的边界。
综上所述, 在实际数据应用中, 可视化倾斜角法和Theta图法相较于总水平导数法能够更好地进行地质体的边界识别, 小波变换结合幂次变换能够很好地起到压制噪声以及收敛边界的作用。
5 结论1) 本文针对数值计算方法在位场数据边界识别中受噪声影响大、识别边界不够收敛的问题, 提出应用小波变换结合幂次变换的方法在原有方法上进行改进, 并选取了3种传统数值计算方法, 将改进方法应用于模型数据和实际重磁数据, 得到了较好的结果。
2) 传统倾斜角法不能直观地显示出目标体的边缘位置, 为了突出目标体的边界, 本文对倾斜角法做进一步的改进, 即可视化倾斜角法, 该方法能够提高边界异常的幅值, 从而提高边界识别的精度。
3) 小波变换方法是将数据分解成近似系数和细节系数, 再对近似系数进行重构, 由于近似系数包含较少的噪声信息, 从而减少噪声对边界识别的影响。
4) 本文提出幂次变换方法对识别出的边界进行有效收敛, 通常幂级数越大, 收敛效果越好, 但由于幂级数过高会丢失细节信息, 因此幂级数选取通常不大于8。
| [1] |
杨高印. 位场数据处理的一项新技术:小子域滤波法[J].
石油地球物理勘探, 1995, 30(2): 240-244.
Yang Gaoyin. A New Technique for Potential-Field Data Processing:Small Sub-Domain Filtering[J]. Oil Geophysical Prospecting, 1995, 30(2): 240-244. |
| [2] | Cooper G R J, Cowan D R. Edge Enhancement of Potential-Field Data Using Normalized Statistics[J]. Geophysics, 2008, 73(3): 1-4. |
| [3] | Hood P, McClure D J. Gradient Measurements in Ground Magnetic Prospecting[J]. Geophysics, 1965, 30(3): 403-410. DOI:10.1190/1.1439592 |
| [4] | Cordell L. Gravimetric Expression of Graben Faulting in Santa Fe Country and the Espanola Basin, New Mexico[C]//New Mexico Geological Society Guidebook, 30th Annual Fall Field Conference. New Mexico: New Mexico Geological, Society, 1979: 59-64. |
| [5] | Nabighian M N. The Analytic Signal of Two-Dimen-sional Magnetic Bodies With Polygonal Cross-Section:Its Properties and Use for Automated Anomaly Interpretation[J]. Geophysics, 1972, 37(3): 507-517. DOI:10.1190/1.1440276 |
| [6] | Miller H G, Singh V. Potential Field Tilt:A New Concept for Location of Potential Field Sources[J]. Journal of Applied Geophysics, 1994, 32(2/3): 213-217. |
| [7] | Wijins C, Perez C, Kowalczyk P. Theta Map:Edge Detection in Magnetic Data[J]. Geophysics, 2005, 70(4): 39-43. DOI:10.1190/1.1988184 |
| [8] |
马国庆, 杜晓娟, 李丽丽. 利用水平与垂直导数的相关系数进行位场数据的边界识别[J].
吉林大学学报(地球科学版), 2011, 41(增刊1): 345-348.
Ma Guoqing, Du Xiaojuan, Li Lili. Edge Detection of Potential Filed Data Using Correlation Coefficients of Horizontal and Vertical Derivatives[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(Sup.1): 345-348. |
| [9] |
马国庆, 黄大年, 于平, 等. 改进的均衡滤波器在位场数据边界识别中的应用[J].
地球物理学报, 2012, 55(12): 4288-4295.
Ma Guoqing, Huang Danian, Yu Ping, et al. Application of Improved Balancing Filters to Edge Identification of Potential Field Data[J]. Chinese Journal of Geophysics, 2012, 55(12): 4288-4295. DOI:10.6038/j.issn.0001-5733.2012.12.040 |
| [10] |
徐亚, 郝天珧, 周立宏, 等. 位场小波变换研究进展[J].
地球物理学进展, 2006, 21(4): 1132-1138.
Xu Ya, Hao Tianyao, Zhou Lihong, et al. Review of Wavelet Transform in Potential Field[J]. Progress in Geophysics, 2006, 21(4): 1132-1138. |
| [11] |
刘彩云. 基于小波变换的位场场源识别与异常分离方法研究[D]. 北京: 中国地质大学, 2014.
Liu Caiyun. The Research on Methods of Edge Detection and Anomaly Separation of Potential Field Source Based on Wavelet Transform[D]. Beijing: China University of Geosciences, 2014. |
| [12] |
张郝. 基于小波变换的图像去噪方法研究[D]. 北京: 北京交通大学, 2008.
Zhang Hao. The Research on Image Denoising Based on Wavelet Transform[D]. Beijing: Beijing Jiaotong University, 2008. |
| [13] |
严奉霞. 小波理论及其在图像边缘检测中的应用[D]. 长沙: 国防科学技术大学, 2003.
Yan Fengxia. Wavelet Theory and Its Application to The Edge Detection of Images[D]. Changsha: National University of Defense Technology, 2003. |
| [14] |
张代磊, 黄大年, 张冲. 基于遗传算法优化的BP神经网络在密度界面反演中的应用[J].
吉林大学学报(地球科学版), 2017, 47(2): 580-588.
Zhang Dailei, Huang Danian, Zhang Chong. Application of BP Neural Network Based on Genetic Algorithm in the Inversion of Density Interface[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(2): 580-588. |
| [15] |
王明, 郭志宏, 何辉, 等. 基于反双曲正切的位场边界识别技术[J].
物探与化探, 2013, 37(4): 655-663.
Wang Ming, Guo Zhihong, He Hui, et al. Edge Detection of Potential Field Data Using Inverse Hyperbolic Tangent[J]. Geophysical and Geochemical Exploration, 2013, 37(4): 655-663. DOI:10.11720/j.issn.1000-8918.2013.4.15 |
| [16] |
冷眉. 重磁资料异常分离与构造边界识别方法的研究及应用[D]. 成都: 成都理工大学, 2014.
Leng Mei. Research and Application of the Method of Separating Anomalous and the Structure Boundary Identification with the Data of Gravity and Magnetic[D]. Chengdu: Chengdu University of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10616-1015522709.htm |



