0 引言
低频电磁法对地幔中的挥发物、流体和部分熔融特别敏感[1], 而地磁测深(GDS)是低频电磁法中一种重要的方法, 成为研究地球地幔深部物理化学性质以及地球动力学的重要技术手段。全球不同地磁台站数据的一维反演结果表明了地幔电性的局部不均匀性[2], 此外, 全球和半全球地磁数据的三维反演也揭示了地幔结构的非一维性[3-4]。例如, Semenovo等[5]利用全球地磁台站数据反演的结果揭示了地幔410~1 600 km, 特别是670~900 km的深度范围内存在广泛的横向不均匀性。Kelbert等[6]通过全球中纬度地区的地磁数据反演得到全球三维电导率模型, 并结合Huang等[7]和Yoshino等[8]的相关实验室测量结果, 认为大洋板块的俯冲作用将大量的水带入转换带, 使得转换带的电导率增大, 说明地幔电性结构的横向变化很大。可见, 地磁数据的一维反演无法获得地幔精细的电性结构, 而通过地磁数据三维反演可以获得比较精细的全球三维电导率模型。然而, 有多种因素影响全球三维电导率模型的可靠性, 例如, 地磁台站空间分布的不均匀性、正演求解精度不够等问题[9]。
全球地磁感应的三维正演是地磁数据反演的核心问题, 也是影响全球三维电导率模型反演的关键因素。为了获得地幔的电性结构, 必须考虑地球形状和外部磁场的空间分布, 即平面波假设不再成立[10], 一般用球谐函数的主要项P10(周期范围105~107 s)模拟外部源。目前适用于全球电磁感应的球坐标系下的三维正演方法主要有积分方程法[11-12]、有限单元法[13-15]、有限差分方法[16-18]、球谐函数法[19]、球谐有限元方法[20-21]。Kelbert等[22]详细对比了这些方法的模拟精度, 结果表明, 不同方法在计算速度和精度方面各具优缺点, 但是不同方法结果基本一致。
国内地磁测深研究取得了丰富的成果, 从20世纪80年代开始, 针对不同地区的地磁数据开展一维反演研究, 获得了一维电导率模型, 揭示了我国地幔的局部电性特征[23-26]。最近, 徐光晶等[27]利用地磁数据转化的等效大地电磁标量阻抗反演得到了我国东部地区的一维地幔电性结构。然而, 国内地磁测深的三维正反演工作研究较少。中国的地磁台站分布广泛, 地磁测深的三维反演对于认识中国地区地幔电性结构和地球动力学具有重要意义, 而正演是反演的核心。因此, 本文介绍全球地磁感应三维正演的基本方法和思路, 基于P10假设, 利用Uyeshima等[16]球坐标系下交错网格有限差分算法, 用PARDISO求解器求解Maxwell方程来计算磁场三分量和地磁响应函数; 然后通过一维模型和南北半球模型, 验证本文正演结果的正确性和精度; 最后通过三维“棋盘模型”来研究三维异常体对磁场分量响应的空间分布规律。
1 正演问题 1.1 数学物理模型在长周期范围, 空气层电导率小于10-10 S/m[28], 介电常数为10-11 F/m, 则传导电流在空气和地层中占主导地位, 忽略位移电流[16]。设时谐因子为eiωt, 频率域Maxwell方程的积分形式为
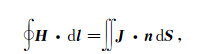 (1)
(1)  (2)
(2) 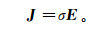 (3)
(3) 式中: 
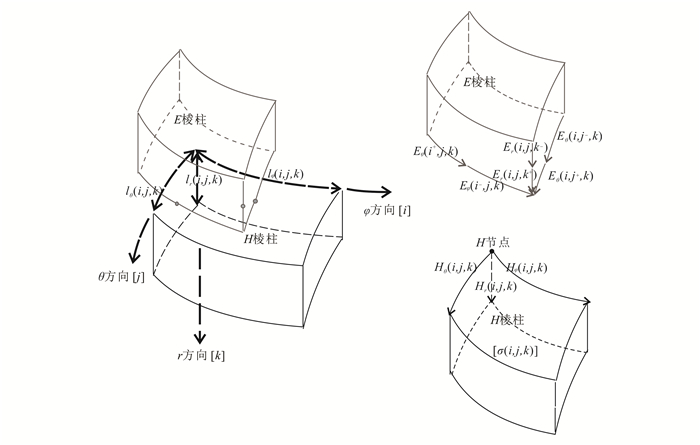
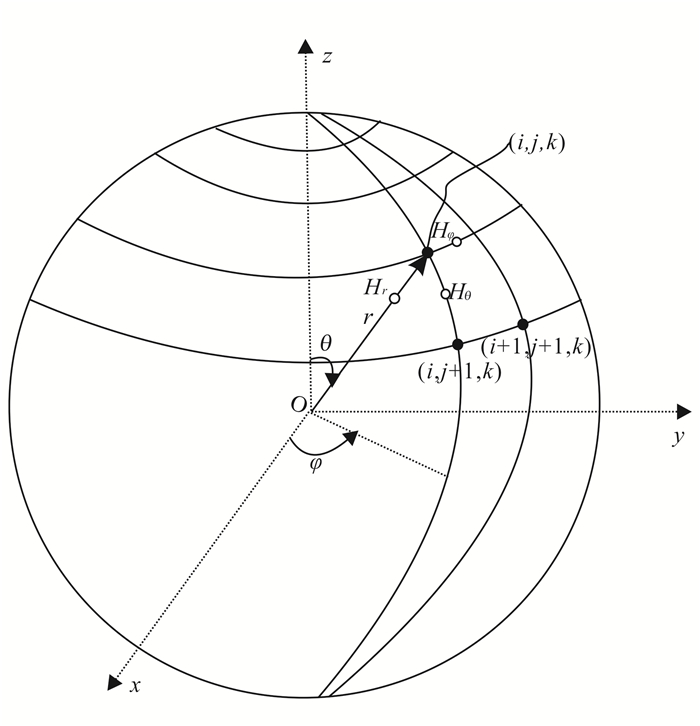
在图 1球坐标下, 采用正交的曲面坐标对地球进行离散。单元节点编号(i, j, k)对应的球坐标为(φ, θ, r), 磁场切向分量Hφ和Hθ分别定义为经度和纬度方向, 且它们的正方向分别指向东和南, 垂直分量Hr定义在半径方向。
|
| 图 1 球坐标系下的磁场分量 Figure 1 Magnetic field defined in a spherical coordinate system |
|
|
边界条件的设置对于计算精度非常重要。空气层的上边界应该离地球足够远, 以保证地球内部产生的二次磁场在源位置产生的干扰衰减掉。本文将计算域的外边界设置在距地心10倍地球半径R(R= 6 371 km)处, 并且将地球以外的“空气层”电导率设为10-10 S/m; 计算域的内边界为核幔边界(CMB), 距离地表 2 871 km, 并且假设地核的电导率为无穷大。在此假设条件下, 地核内磁场切向分量为零, 但是核幔边界处磁场切向分量不为零。
外源的加载非常关键。在中、低纬度地区, 我们使用P10项来模拟磁层的等效环形电流[2]。根据式(1), 将环形电流在计算域上边界的值赋给磁场切向分量的环形积分, 从而近似模拟电磁层和磁层的外源, 即求解Dirichlet边界问题。
1.2 球坐标系下交错网格有限差分与传统的直角坐标系交错网格有限差分[29]不同的是, 本文采用Uyeshima等[16]的交错网格有限差分策略, 将整个球体剖分为表面弯曲的六面体棱柱, 网格单元如图 2所示。假设单元网格内的电导率值均匀。对第(i, j, k)棱柱, 磁场三分量分别被定义在棱边上, 因此这些棱柱、棱边和节点分别称为H棱柱、H棱边和H节点。φ(i)、θ(j)和r(k)分别是第(i, j, k)个H节点处的经度、余纬度和到地心的距离。用L、M、N分别代表φ、θ、r方向的H棱柱数, 则i∈[1, L]; j∈[1, M+1];k∈[1, N+1]。用Hφ(i, j, k)、Hθ(i, j, k)和Hr(i, j, k)分别表示第(i, j, k)个H棱边的磁场分量。用同样方法定义电场。但电场法向分量在电导率不同的单元边界是不连续的, 因此在边界的两侧需要分别定义, 例如, 与磁场Hθ(i, j, k)对应的电场定义为Eθ(i, j-, k)和Eθ(i, j+, k)。
定义H棱边φ、θ、r三个方向的长度分别为lφ(i, j, k)、lθ(i, j, k)和lr(i, j, k), 具体的计算公式为:
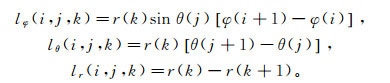 (4)
(4) 同样, H棱柱三个方向的表面积表示为:
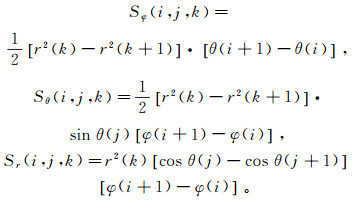 (5)
(5) 利用式(4)和式(5)对Maxwell方程(1)、(2)、(3)分别进行离散(详细过程参考文献[16]), 最后得到磁场解的三个分量满足矩阵方程:
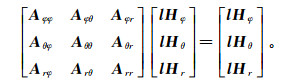 (6)
(6) 式中, 矢量lH包含磁场的线积分。加入源后, 代表边界场值的常数移到方程的右端项, 即包含在矢量lH中。Aθφ与磁场φ分量的线积分以及磁场θ分量的边界值有关, 其余类推。由Aθφ等子单元矩阵组成最终的系数矩阵A。系数矩阵A是稀疏对称的、并且矩阵A除了其对角线元素外都是实数[16]。最后, 对方程(6)式进行求解可以得到磁场分量。与Uyeshima等[16]采用的最小残差加速(MRA)迭代法求解方程不同的是, 本文利用求解速度更快的PARDISO求解器求解, 避免了迭代求解过程中的散度校正[30], 同时也保证了求解精度和稳定性。
1.3 全球地磁响应函数假设源为带状环形源[2], 根据Schultz等[31]地磁响应函数的定义, 由地表某点的磁场垂直和纬度方向分量, 定义地磁测深中C响应为
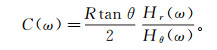 (7)
(7) 式中:tanθ为源空间结构的补偿项, 因此一维情况下C响应在地球表面的任意位置都是相同的; 在空间某点上, Hr是指向地心的磁场垂直分量; Hθ是指向地磁南极的磁场余纬度分量。一般情况下C响应的实部为正值, 虚部为负值, 并且可以在一定程度上反映深度与电阻率的关系[32]。
为了更好地描述地下电性结构的横向不均匀性, Fujii等[33]提出D响应, 其定义为
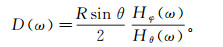 (8)
(8) 式中, Hφ是指向东的磁场沿经度方向分量。D响应在一维结构下为零, 且横向不均匀性越强, D响应的值越大。
2 精度验证三维有限差分模拟分别采用了36×18×54、72×36×78、180×90×98、360×180×118不同的粗细网格, 发现不同网格的C响应相对误差在1%以内。综合计算精度和速度, 下文数值模拟采用的网格为180×90×98, 即地球在经纬度方向被剖分为2°×2°、半径方向被剖分为98层, 其中空气层为17层。计算机主频为3.2 GHz, Intel处理器, 内存8 G。实际单个频点计算占用内存约3 G, 单频计算时间大约20 min。
2.1 一维模型C响应是地磁测深应用最广泛的响应函数, 本文验证周期范围从数小时到3 a的C响应, 选取35个对数均匀分布的频率。一维模型电性结构如Medin等[34], 其参数如表 1所示。一维解析解采用李世文等[35]的层状地球地表C响应算法, 验证对比所用三维有限元正演结果来自Ribaudo等[15]。图 3a给出了本文有限差分算法数值精度验证情况, 可以看出, 有限差分得到的响应与解析解以及有限元模拟响应基本吻合。图 3b给出了有限差分数值解和一维解析解的相对误差, 从图可见:C响应实部误差都小于2%;虚部相对误差大于实部误差, 最大也仅为4.8%, 且比较大的误差出现在1~10 d的小周期范围以及大于100 d的超长周期。
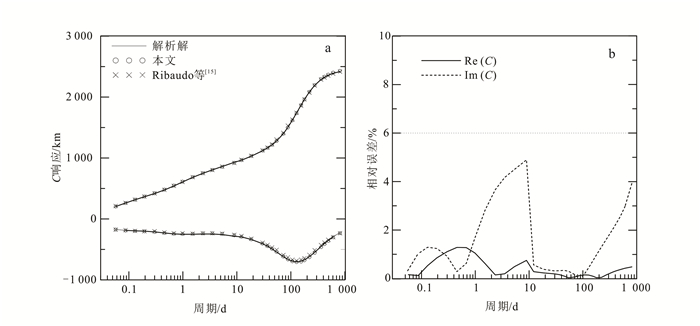
|
| a.不同周期1D模型C响应, 正值是C的实部, 负值是C的虚部; b.本文有限差分解和一维解析解的相对误差。 图 3 球坐标系中交错网格有限差分算法的一维模型精度验证结果 Figure 3 Precision validation result of the 1D model for the staggered-grid FD formulation in spherical coordinate system |
|
|
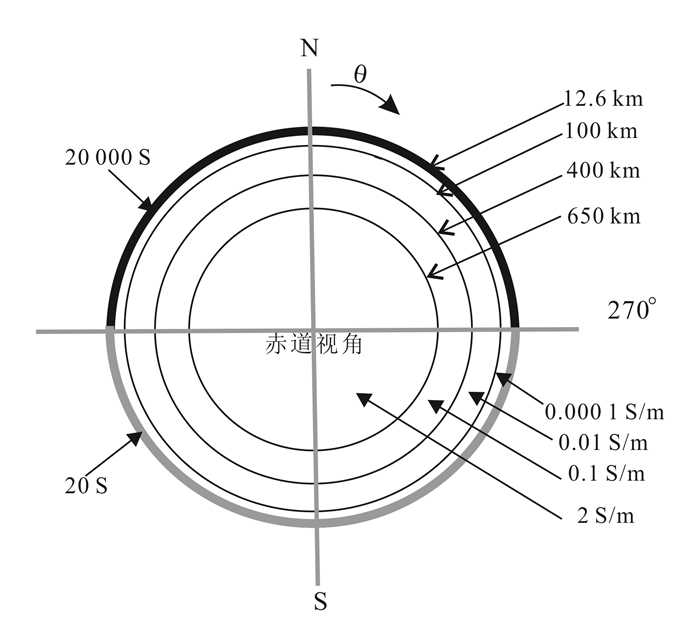
双半球模型在全球电磁感应正演模拟精度验证中被广泛采用[16, 22], 本文以南北(NS)双半球模型(图 4)为例进行验证。半球模型由一维电性结构模型和地表无限薄的非均匀电导层组成。对于NS半球模型, 北半球(余纬度0°~90°)薄层电导为20 000 S, 南半球(余纬度90°~180°)薄层电导为20 S, 薄层厚度设为12.6 km。
图 5给出了本文有限差分算法在周期为4 d的磁场水平南向分量和垂直分量曲线。由图 5可知, 本文计算结果与Kelbert等[21]的结果一致, 说明了本文三维正演的精确性和可靠性。
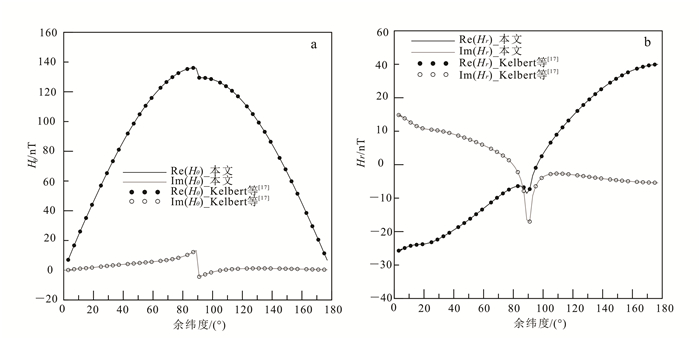
|
| 图 5 周期为4 d的南北双半球模型响应 Figure 5 Response of North/South hemispheres at period 4 d |
|
|
与传统数值模拟中异常体边界的电性突变不同, “棋盘模型”(checkerboard model)不仅可以模拟地球横向电导率的三维不均匀性, 并且能很好地模拟局部异常体电阻率的连续性变化, 对电磁法数值模拟更具有挑战性[22]。棋盘模型通过球谐函数(SHFE)
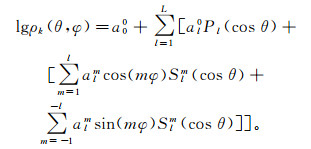 (9)
(9) 实现。式中:Slm是施密特半标准化连带勒让德函数; l、m是球谐阶数和次数; ρ为电阻率; k为地层序号; a为球谐系数。
本文在表 1所示一维模型的第二层, 即在400~800 km深度的中低纬度进行球谐扰动。选择球谐系数l=12、m=8来模拟横向空间不均匀性, 形成的“棋盘模型”如图 6所示。
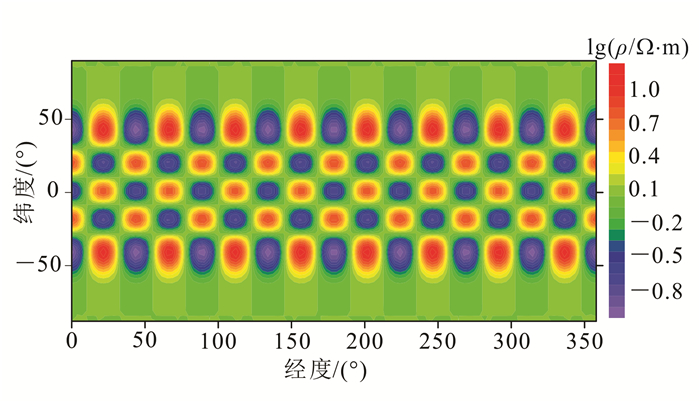
|
| 图 6 l=12, m=8时的棋盘模型 Figure 6 Synthetic degree 12 order 8 checkerboard model |
|
|
图 7为周期为4 d时“棋盘模型”地球表面的磁场三分量的数值模拟结果。由图 7可见:Hφ对模型的横向分辨率能力最好, 尤其是Hφ的虚部对棋盘模型的边界分辨能力更强, 但是, Hφ反映不出来异常体的位置且在幅值上小于Hθ和Hr; Hθ的虚部响应和棋盘模型(尤其是低阻异常)的位置对应关系非常好, 但实部分辨能力很差, 且虚部数值比实部小很多; Hr的分辨能力较差, 但实部和虚部对异常体的分辨能力相当。
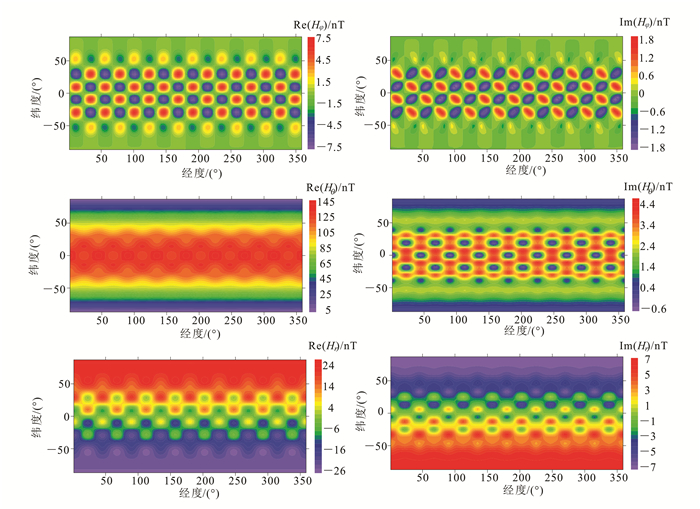
|
| 图 7 周期4 d的地表磁场三分量实部和虚部 Figure 7 Real and imaginary parts of the three components of magnetic at earth surface at period of 4 d |
|
|
此外, 由C响应和D响应的定义式(7)和式(8)可知, Hθ和Hr决定C响应的大小, 而D响应中包含了对三维分辨能力更强的Hφ分量, 这也印证了D响应的横向分辨率要优于C响应。但实测数据的D响应容易受干扰影响[36], 所以现在对D响应的应用较少。随着仪器技术和信号处理技术的发展, D响应未来可以被广泛应用。总之, 磁场分量能够分辨出棋盘模型的异常体的大小和准确的位置。
4 讨论与结论本文在前人的基础上, 利用球坐标系下的交错网格有限差分技术, 对Maxwell方程的积分形式进行离散, 利用PARDISO求解器求解稀疏对称矩阵方程, 获得了全球电磁感应三维正演精确的数值解。
分别通过一维模型和双半球模型的精度验证, 说明了本文数值模拟的正确性和精度; 三维“棋盘模型”结果表明地表磁场分量对异常体具有很好的分辨能力, Hφ分量对异常体的边界分辨能力更强, 而Hθ分量和异常体的位置对应关系非常好。同时, D响应比C响应对三维异常体分辨能力更强, 随着技术的发展, D响应同样具有重要的研究价值。
针对超长周期的地磁测深三维反演, 直角坐标系无法适用, 本文的球坐标系三维正演为地磁测深三维反演提供了技术基础, 对利用地磁数据获得中国或全球地幔电性结构, 从而研究地球演化和地球动力学过程具有重要意义。
致谢: 美国地质调查局的Anna Kelbert研究员在本文数值模拟研究工作中提供了热情帮助, Intel Fortran数学库MKL提供了PARDISO求解器, 在此一并致谢。| [1] | Karato S I. Remote Sensing of Hydrogen in Earth's Mantle[J]. Reviews in Mineralogy & Geochemistry, 2006, 62(1): 343-375. |
| [2] | Schultz A. On the Vertical Gradient and Associated Heterogeneity in Mantle Electrical Conductivity[J]. Phys Earth Planet Int, 1990, 64(1): 68-86. DOI:10.1016/0031-9201(90)90006-J |
| [3] | Utada H, Koyama T, Obayashi M, et al. A Joint Interpretation of Electromagnetic and Seismic Tomography Models Suggests the Mantle Transition Zone Below Europe is Dry[J]. Earth Planet Sci Lett, 2009, 281(3/4): 249-257. |
| [4] | Shimizu H, Utada H, Baba K, et al. Three-Dimen-sional Imaging of Electrical Conductivity in the Mantle Transition Zone Beneath the North Pacific Ocean by a Semi-Global Induction Study[J]. Phys Earth Planet Int, 2010, 183(1/2): 252-269. |
| [5] | Semenov A, Kuvshinov A. Global 3-D Imaging of Mantle Conductivity Based on Inversion of Observatory C-Responses:Ⅱ:Data Analysis and Results[J]. Geophysical Journal International, 2012, 191(3): 965-992. |
| [6] | Kelbert A, Schultz A, Egbert G. Global Electromag-netic Induction Constraints on Transition-Zone Water Content Variations[J]. Nature, 2009, 460: 1003-1006. DOI:10.1038/nature08257 |
| [7] | Huang X, Xu Y, Karato S I. Water Content in the Transition Zone from Electrical Conductivity of Wadsleyite and Ringwoodite[J]. Nature, 2005, 434: 746-749. DOI:10.1038/nature03426 |
| [8] | Yoshino T, Manthilake G, Matsuzaki T, et al. Dry Mantle Transition Zone Inferred from the Conductivity of Wadsleyite and Ringwoodite[J]. Nature, 2008, 451: 326-329. DOI:10.1038/nature06427 |
| [9] | Sun J, Egbert G. A Thin-Sheet Model for Global Electromagnetic Induction[J]. Geophysical Journal International, 2012, 189(1): 343-356. DOI:10.1111/gji.2012.189.issue-1 |
| [10] | Schmucker U. A Spherical Harmonic Analysis of Solar Daily Variations in the Years 1964-1965:Response Estimates and Source Fields for Global Induction:Ⅰ:Methods[J]. Geophysical Journal International, 1999, 136(2): 439-454. DOI:10.1046/j.1365-246X.1999.00742.x |
| [11] | Koyama T, Khan A, Kuvshinov A. Three-Dimen-sional Electrical Conductivity Structure Beneath Australia from Inversion of Geomagnetic Observatory Data:Evidence for Lateral Variations in Transition-Zone Temperature, Water Content and Melt[J]. Geophysical Journal International, 2014, 196(3): 1330. DOI:10.1093/gji/ggt455 |
| [12] | Kuvshinov A. 3-D Global Induction in the Oceans and Solid Earth:Recent Progress in Modeling Magnetic and Electric Fields from Sources of Magnetospheric, Ionospheric and Oceanic Origin[J]. Surveys in Geophysics, 2008, 29(2): 139-186. DOI:10.1007/s10712-008-9045-z |
| [13] | Everett M E, Schultz A. Geomagnetic Induction in a Heterogeneous Sphere:Azimuthally Symmetric Test Computations and the Response of an Undulating 600-km Discontinuity[J]. J Geophys of Research Atmospheres, 1996, 101(B2): 2765-2783. DOI:10.1029/95JB03541 |
| [14] | Yoshimura R, Oshiman N. Edge-Based Finite Element Approach to the Simulation of Geoelectromagnetic Induction on a 3-D Sphere[J]. Geophys Res Lett, 2002, 29(3): 1-4. |
| [15] | Ribaudo J T, Constable C G, Parker R L. Scripted Finite Element Tools for Global Electromagnetic Induction Studies[J]. Geophysical Journal International, 2012, 188(2): 435-446. DOI:10.1111/gji.2012.188.issue-2 |
| [16] | Uyeshima M, Schultz A. Geoelectromagnetic Induc-tion in a Heterogeneous Sphere:A New Three-Dimensional Forward Solver Using a Conservative Staggered-Grid Finite Difference Method[J]. Geophysical Journal International, 2000, 140(3): 636-650. DOI:10.1046/j.1365-246X.2000.00051.x |
| [17] | Kelbert A, Egbert G D, Schultz A. Non-Linear Conjugate Gradient Inversion for Global EM Induction:Resolution Studies[J]. Geophysical Journal International, 2008, 173(2): 365-381. DOI:10.1111/gji.2008.173.issue-2 |
| [18] | Weiss C J. Triangulated Finite Difference Methods for Global-Scale Electromagnetic Induction Simulations of Whole Mantle Electrical Heterogeneity[J]. Geochemistry Geophysics Geosystems, 2010, 11(11): 129-143. |
| [19] | Tarits P, Mande A M. The Heterogeneous Electrical Conductivity Structure of the Lower Mantle[J]. Physics of the Earth & Planetary Interiors, 2010, 183(1/2): 115-125. |
| [20] | Martinec Z. Spectral-Finite Element Approach to Three-Dimensional Electromagnetic Induction in a Spherical Earth[J]. Geophysical Journal International, 1999, 136(1): 229-250. DOI:10.1046/j.1365-246X.1999.00713.x |
| [21] | Velímsk J, Martinec Z. Time-Domain, Spherical Harmonic-Finite Element Approach to Transient Three-Dimensional Geomagnetic Induction in a Spherical Heterogeneous Earth[J]. Geophysical Journal International, 2005, 161(1): 81-101. DOI:10.1111/gji.2005.161.issue-1 |
| [22] | Kelbert A, Kuvshinov A, Velímsk J, et al. Global 3-D Electromagnetic Forward Modelling:A Benchmark Study[J]. Geophysical Journal Internationa, 2014, 197(2): 785-814. DOI:10.1093/gji/ggu028 |
| [23] |
陈伯舫. 中国东南部地幔高导层的埋藏深度[J].
地震学报, 1986, 8(2): 172-178.
Chen Bofang. Buried Depth of the High Conductivity Layer Beneath the Region of South-East China[J]. Acta Seismologica Sinica, 1986, 8(2): 172-178. |
| [24] |
杜兴信, 鲁秀玲. 用单台Z/H法研究陕西地区深部电导率[J].
内陆地震, 1994, 8(4): 333-338.
Du Xingxin, Lu Xiuling. Investigation on Deep Electroconductivity of Shaanxi Region by Means of Z/H Method with Single Station[J]. Inland Earthquake, 1994, 8(4): 333-338. |
| [25] |
范国华, 姚同起, 顾左文, 等. 利用磁梯度法研究我国地幔导电率[J].
地震学报, 1997, 19(2): 164-173.
Fan Guohua, Yao Tongqi, Gu Zuowen, et al. Research on Mantle Conductivity of China with Gradient Method[J]. Acta Seismologica Sinica, 1997, 19(2): 164-173. |
| [26] |
赵国泽, 汤吉, 梁竞阁, 等. 用大地电磁网法在长春等地探测上地幔电导率结构[J].
地震地质, 2001, 23(2): 143-152.
Zhao Guoze, Tang Ji, Liang Jingge, et al. Measurement of Network-MT in Two Areas of NE China for Study of Upper Mantle Conductivity Structure of the Back-Arc Region[J]. Seismology and Geology, 2001, 23(2): 143-152. |
| [27] |
徐光晶, 汤吉, 黄清华, 等. 华北地区上地幔及过渡带电性结构研究[J].
地球物理学报, 2015, 58(2): 566-575.
Xu Guangjing, Tang Ji, Huang Qinghua, et al. Study on the Conductivity Structure of the Upper Mantle and Transition Zone Beneath North China[J]. Chinese Journal of Geophysics, 2015, 58(2): 566-575. DOI:10.6038/cjg20150219 |
| [28] | Rokityansky I I. Geoelectromagnetic Investigation of the Earth's Crust and Mantle[M]. Berlin: Springer-Verlag, 1982. |
| [29] |
李大俊, 翁爱华, 杨悦, 等. 地-井瞬变电磁三维交错网格有限差分正演及响应特性[J].
吉林大学学报(地球科学版), 2017, 47(5): 1552-1561.
Li Dajun, Weng Aihua, Yang Yue, et al. Three-Dimension Forward Modeling and Characteristics for Surface-Borehole Transient Electromagnetic by Using Staggered-Grid Finite Difference Method[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(5): 1552-1561. |
| [30] | Smith J T. Conservative Modeling of 3-D Electromag-netic Fields:Part 1:Properties and Error Analysis[J]. Geophysics, 1996, 61(5): 1308-1318. DOI:10.1190/1.1444054 |
| [31] | Schultz A, Larsen J C. On the Electrical Conductivity of the Mid-Mantle:Ⅰ:Calculation of Equivalent Scalar Magnetotelluric Response Functions[J]. Geophysical Journal International, 1987, 88(3): 733-761. DOI:10.1111/j.1365-246X.1987.tb01654.x |
| [32] | Schmucker U. Substitute Conductors for Electromag-netic Response Estimates[J]. Pure and Applied Geophysics, 1987, 125(2): 341-367. |
| [33] | Fujii I, Schultz A. The 3D Electromagnetic Response of the Earth to Ring Current and Auroral Oval Excitation[J]. Geophysical Journal International, 2002, 151(3): 689-709. DOI:10.1046/j.1365-246X.2002.01775.x |
| [34] | Medin A E, Parker R L, Constable S. Making Sound Inferences from Geomagnetic Sounding[J]. Physics of the Earth & Planetary Interiors, 2007, 160(1): 51-59. |
| [35] |
李世文, 翁爱华, 李建平, 等. 浅部约束的地磁测深C-响应一维反演[J].
地球物理学报, 2017, 60(3): 1201-1210.
Li Shiwen, Weng Aihua, Li Jianping, et al. 1-D Inversion of C-Response Data from Geomagnetic Depth Sounding with Shallow Resistivity Constraint[J]. Chinese Journal of Geophysics, 2017, 60(3): 1201-1210. DOI:10.6038/cjg20170330 |
| [36] | Shimizu H, Koyama T, Baba K. Three-Dimensional Geomagnetic Response Functions for Global and Semi-Global Scale Induction Problems[J]. Geophysical Journal International, 2009, 178(1): 123-144. DOI:10.1111/gji.2009.178.issue-1 |