0 引言
探地雷达是以地下介质的电磁特性差异为基础的地球物理探测技术,其通过发射天线发送脉冲波形式的高频电磁波[1]。电磁波在地下介质传播过程中,遇到存在电磁特性差异的界面时便发生反射,返回的电磁波被接收后,通过对信号进行处理,形成雷达时间剖面图[2];然后根据图中信号强度、波形、双程走时等参数分析探测目标体的空间位置、电性状况与几何形态等[3]。按照工作方式的不同,探地雷达分为地面探地雷达和钻孔雷达[4]。钻孔雷达通过将雷达天线置于钻孔中进行探测,天线更接近地下目标体,具有更大的探测范围和分辨率[5]。相对于地面雷达,钻孔雷达仪器在井中的探测范围得到较大的扩展, 在相对导电的岩石中, 探测范围可达10~20 m[6]。钻孔雷达的发展历程大致如下:1978年,Rubin等[7]在辉绿岩中进行了钻孔雷达实验;1980年国际STRIPA(international stripa project)计划开始实行, 瑞典RAMAC钻孔雷达系统则是在该计划下开发完成的[8];20世纪90年代后, 日本东北大学Sato等[9]研究开发了极化钻孔雷达系统, 能够进行井下的全极化测量。
传统的钻孔雷达发射天线和接收天都是全方位的[10],因此,其只能探测目标地质体深度以及其距井孔的距离,并不能对其方位进行探测。目前,对地下介质进行三维立体成像仍然是一件非常困难的事情。为了解决这个问题,发展了定向钻孔雷达技术。
定向钻孔雷达不仅可以探测目标的深度和距井孔距离,而且可以探测其方位。定向钻孔雷达的实现一般有两种方式:其一是用阵列天线接收的方式进行测量,主要使用均匀圆阵,根据不同的波至时间提取方位信息;其二是采用定向发射天线的方式,天线向井周定向发射电磁波,目标体的方位位于电磁波的发射方向[11]。
对于以上两种定向钻孔雷达系统,人们分别开发了相应的数据处理方法。对于第一种定向钻孔雷达系统,即用阵列天线接收的定向钻孔雷达系统,采用分析各个接收天线所接收到波形的先后次序来分析反射波的方位信息;对于第二种定向钻孔雷达系统,天线以一定的角度发射电磁波,如果该角度下接收天线可以接收到信号,说明该方位存在目标地质体,否则,该方位不存在目标地质体[12]。
本文针对的是第一种定向钻孔雷达系统的实现方式,包括1个发射天线和4个接收天线,4个天线分布于一个垂直于井眼的圆环位置上,呈等角度分布(图 1)。为了分析方便,我们把4个天线指定为东、南、西、北4个方向,顺时针旋转。当北天线方向和地理正北一致时,其余天线分别和东、西、南一致,否则会有偏差角,这可以通过测量北天线相对于地理正北的夹角来校正。针对这种系统,2000年,Ebihara等[13]引入MUSIC算法进行数据处理,取得了较好的效果,同时确定了MUSIC算法在低信噪比情况下的局限性。2007年,Takayama等[14]利用反正切法进行数据处理。2013年,Ebihara等[15]提出了使用计算残差来确定目标方位的算法,该算法对信号由信源到达圆阵中心的时间和入射角进行残差法拟合,来求取入射方位,但只能对一个信源信号进行方位识别处理。
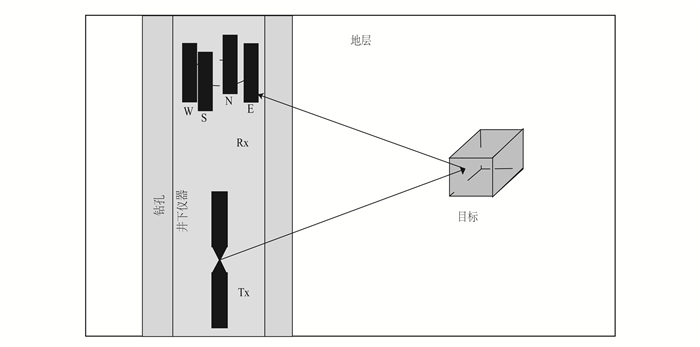
|
| Tx.发射天线;Rx.接收天线。 图 1 单发-四收定向钻孔雷达示意图 Figure 1 Single-transmitter four-receiver borehole rada |
|
|
本文改进残差法算法,采用设计窗口逐点移动的办法,直接计算信号由信源到达圆阵中心时间,仅对方位角进行残差法拟合。这样,一方面大幅提高了算法的运算速度,另一方面,可以对任意多个信源信号进行处理。同时,本文提出并实现了利用方位角数据合成横向切片和纵向切片的算法,再利用所得的纵横切片合成三维数组, 再利用所得的三维数组对地质体进行三维成像的算法,获得三维成像结果。
1 改进的残差法算法Ebihara等[15]提出了使用残差法对入射信号进行方位估计的算法,主要是针对在一个钻孔中同轴线馈电的偶极天线阵列,如图 2所示。算法包括如下假设:只有一个入射信号入射到天线阵元中;各个天线阵元接收到的信号不发生畸变;各个阵元的噪声水平是相同的。在选取方位角时,取正北方向为0°,顺时针方向为正方向,因此,第i个天线阵元接收到信号的时间ti可以表示为
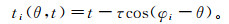 (1)
(1)
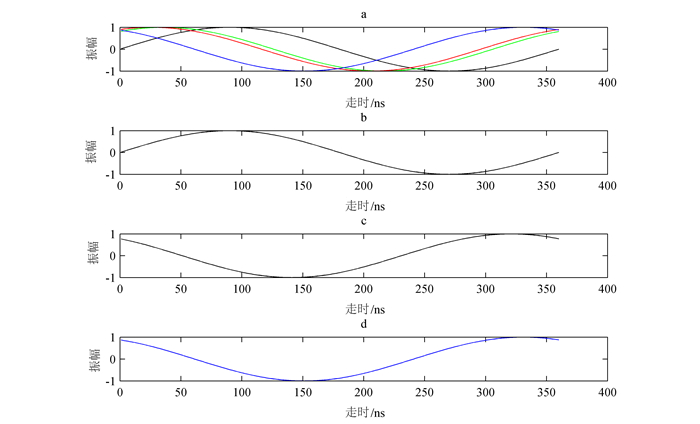
|
| a.各方位接收天线接收信号;b.北向接收天线接收信号; c.改变θ和t北向接收天线接收信号;d.南向接收天线接收信号。 图 2 残差法波形示意图 Figure 2 Waveform of residual algorithm |
|
|
式中:t为波传到圆阵中心所用的时间;τ为电磁波在两个天线阵元之间最大传播时间的一半,即如果圆阵半径为r,电磁波的传播速度为v,那么τ=r/v;φi为第i个天线阵元所在的方位角;θ为入射波的方位角。将第i个天线阵元所接收到的实测数据定义为ti,每一个t和θ的改变值对应数据信号为fi。假设共有N个采样点,接收天线的数目为M,在本文中,由于存在4个接收天线,因此M为4。通过一定范围内对于t和θ的改变,找到使得测量值与计算值的残差达到最小的情况,即使得残差
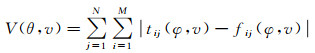 (2)
(2) 最小。式中:tij表示第i个接收天线在第j个采样点的实测时间数据;fij表示每一个v和θ的改变值在第i个接收天线在第j个采样点对应的拟合信号。最小残差所对应的t和θ组合即为所求结果。可以看出,在一个深度,只有一个方位。
本文改进该算法,通过选取宽度为w的窗口(图 3),只对窗口中的信号求取残差,这样,可以对任意多信源进行处理,而之前的残差法只能对一个信源信号进行处理。将窗口内求取的方位角赋值给φk,公式为
 (3)
(3)
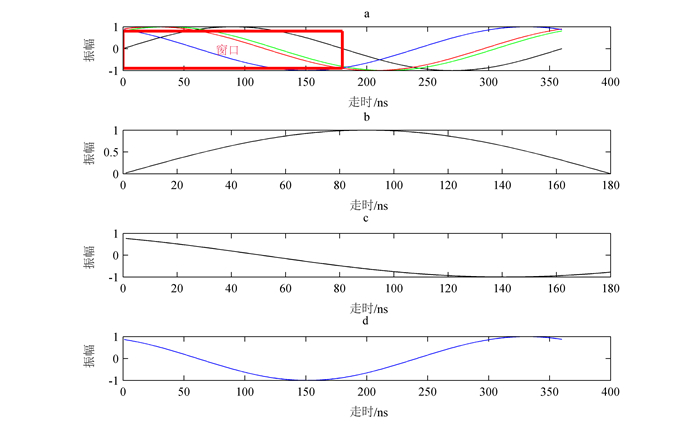
|
| a.各方位接收天线接收信号;b.窗口内北向接收天线接收信号; c.改变θ之后的北向接收天线接收信号;d.南向接收天线接收信号。 图 3 改进的残差法示意图 Figure 3 Theory of improved residual algorithm |
|
|
其中:φk为窗口中央点的方位角;k为该道窗口中央的采样点号;φrk为在一定的窗口下利用残差法求取方位角,即
 (4)
(4) 本方法使得t可以通过窗口中心的走时直接计算得出,即t=kdt,其中dt为时间采样间隔。而之前的残差法需要对t、θ两个变量进行残差拟合求出。
先假设入射角为1°,2°,…,360°,分别计算各个天线的接收数据;然后用实测数据与理论数据的差计算绝对值,残差最小所对应的方位角即为目标方位角。
残差法的具体算法如下:
1) 输入圆阵半径r、采样时间间隔dt等参数,东、南、西、北4个接收天线所接收到的信号为TEm、TSm、TWm、TNm。
2) 选取一定大小的窗口,对接收到的信号进行处理。数据处理前要设定一个阈值,当信号大于阈值才算作有用信号,否则视为噪声。
3) 如图 4所示,选取北向接收天线作为理论计算的标准。假设入射角为θ,阵列半径为r,那么北向接收天线与东向接收天线的时间差为
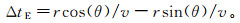 (5)
(5)
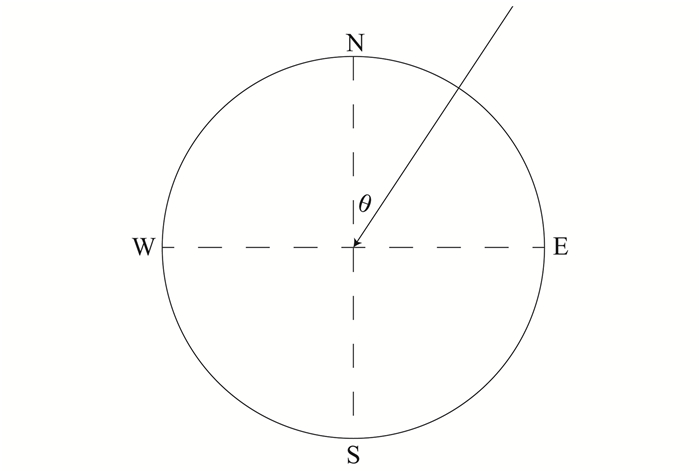
|
| 图 4 残差法计算示意图 Figure 4 Theory of residual algorithm |
|
|
时间差所对应的采样点数为ΔnE=ΔtE/dt。
于是, 东向接收天线的计算数据为
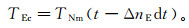 (6)
(6) 北向接收天线与南向接收天线的时间差为
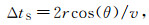 (7)
(7) 时间差所对应的采样点数为ΔnS=ΔtS/dt,于是,南向接收天线的计算数据为
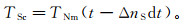 (8)
(8) 西向接收天线与东向接收天线的时间差为
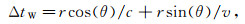 (9)
(9) 时间差所对应的采样点数:ΔnW=ΔtW/dt,于是,西向接收天线的计算数据为
 (10)
(10) 4) 最后计算残差:
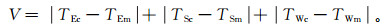 (11)
(11) 最小残差所对应的角度即为方位角。
残差法算法进行方位识别的主要原理是利用4个接收天线所接收信号的相对位置计算方位角。一旦信噪比过低,导致4个接收天线接收到信号的相对位置发生较大的变化,必然影响方位识别结果。如果信号中存在少量噪声,对于4个接收天线接收到信号的相对位置并无太大影响,那么残差法算法依然可以得到非常好的计算结果。
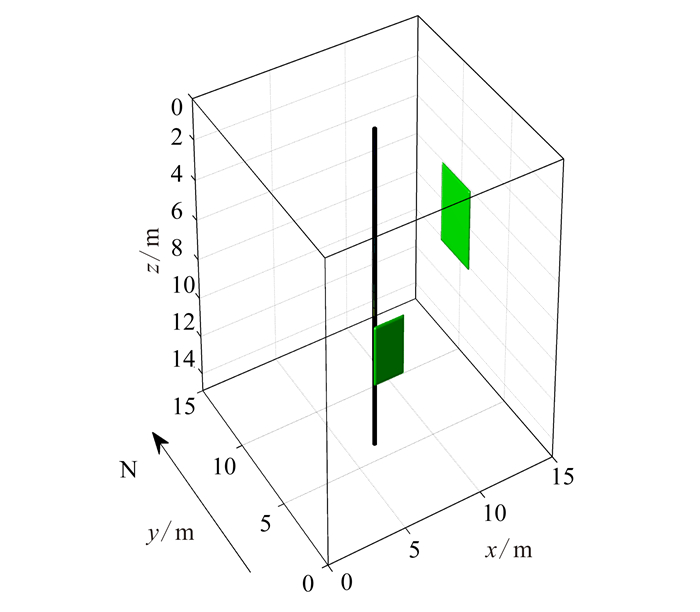
2 合成数据算例用GprMax合成数据[16],其模型包括2个裂缝,一个裂缝在正东方向,另一个裂缝在正南方向,具体如图 5所示。本模型包含2个目标地质体,由于传统的残差法不符合“只有一个入射信号入射到天线阵元中”的假设,因此是无法进行方位识别的。利用该模型验证改进的残差法的有效性,模型参数如表 1、表 2所示,围岩为花岗岩,裂缝内为水。作为探地雷达的目标探测而言,最重要的2项参数是相对介电常数和电导率。
|
| 图 5 用于钻孔雷达合成数据的模型 Figure 5 Model for the borehole radar synthetic data |
|
|
| 相对介电常数 | 电导率/(S/m) | 相对渗透率 | 磁导率/(H/m) | |
| 花岗岩 | 5 | 0.000 7 | 1 | 0 |
| 水 | 80 | 0.700 0 | 1 | 0 |
| d x/m | d y/m | d z/m | 时窗/ns | 阵列半径/m | 收发距/m | 天线主频/MHz | 移动步长/m | 移动次数 |
| 0.1 | 0.1 | 0.1 | 320 | 0.1 | 2.5 | 100 | 0.1 | 100 |
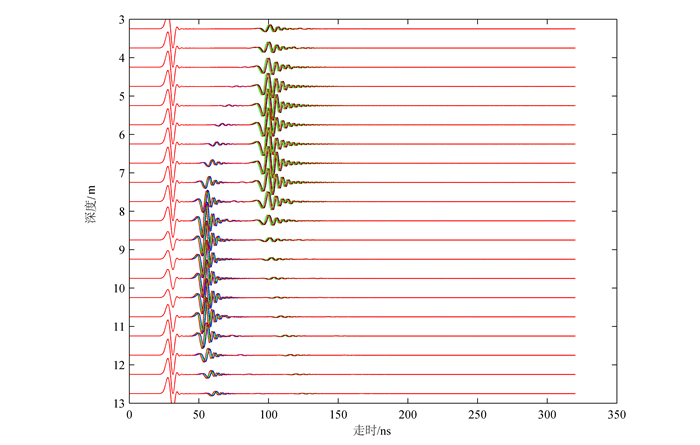
模型对应的波形如图 6所示,发射天线的起始深度为14.00 m,接收天线的起始深度为11.00 m,发射天线与接收天线的中间位置的起始深度为12.75 m,接收天线的4个阵元分别位于东、南、西、北4个方位,发射天线和接收天线均不考虑形状,为点发射点接收,探地雷达由井底向井口移动。从图 6可以清楚看到2个反射信号,距离井眼近的信号为正南方向的裂缝引起的反射波,距离井眼较远的信号为正东方向的裂缝所引起,与模型相符合。数据处理前,首先要去除直达波,将深度为12.25 m到12.75 m的五道前270个采样点的平均波形作为直达波,从记录中减去便可实现直达波的消除。
|
| 图 6 各天线雷达信号波形 Figure 6 Signals for four antennas |
|
|
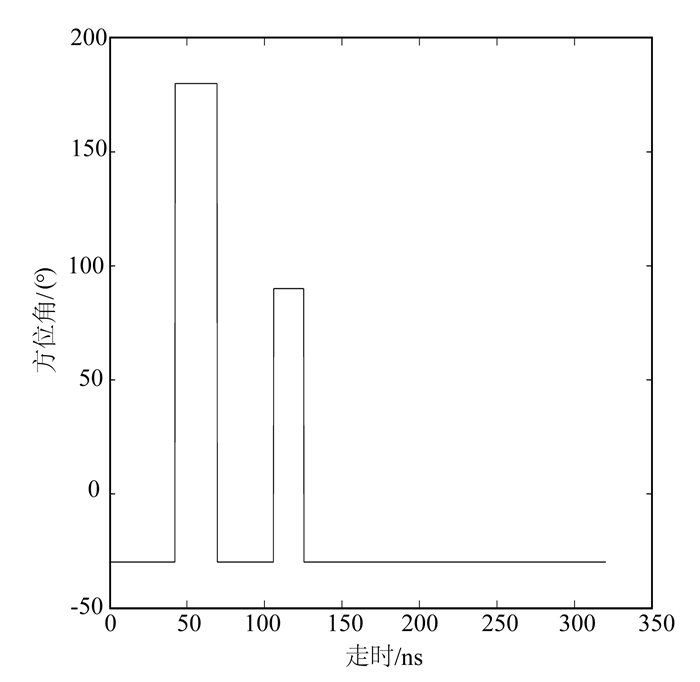
利用残差法计算方位角,选取11.75 m深度处的道的方位识别结果进行显示,如图 7所示。从图 7可以清楚看到:在50~100 ns处有一个信号,方位角为180°,即正南方向;在100~150 ns处有一个信号,方位角为90°,为正东方向,与模型吻合。
|
| 图 7 深度为11.75 m的方位识别结果图 Figure 7 Azimuth angle trace at the depth of 11.75 m |
|
|
利用计算的方位角合成纵横切片数据,基本流程如下:
1) 设计一个三维数组,让道数、方位角数和采样点数为三维数组的3个维数。
2) 根据各道的方位角数据和接收到的电场数据对三维数组进行赋值。
3) 对某一道对应的其他两维数据进行显示,得到该道的横向切片图。对某一个方位对应的各道各采样点的数据进行显示,得到该方位的纵向切片数据。
4) 对于该三维数组中的数据进行显示,得到该模型的三维成像结果图。
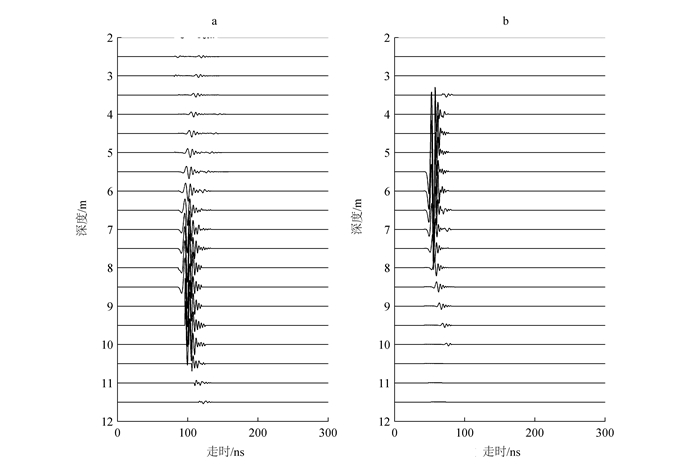
选取第11.75 m处的道,其横向切片如图 8所示。从该切片图中可以明显看出正东方向存在一个异常,正南方向存在一个异常,与模型相符合。90°纵向切片如图 9a所示,可以很明显看到一个异常,因此和模型正东方向的裂缝吻合良好;180°纵向切片如图 9b所示,从图中很明显看到一个异常,与模型正南方向吻合良好。说明残差法取得了非常好的效果。
|
| 图 8 第10道切片图(深度11.75 m) Figure 8 Horizontal cross-section at the depth of 11.75 m |
|
|
|
| a.90°纵向切片;b. 180°纵向切片。 图 9 纵向切片示意图 Figure 9 Vertical cross-section |
|
|
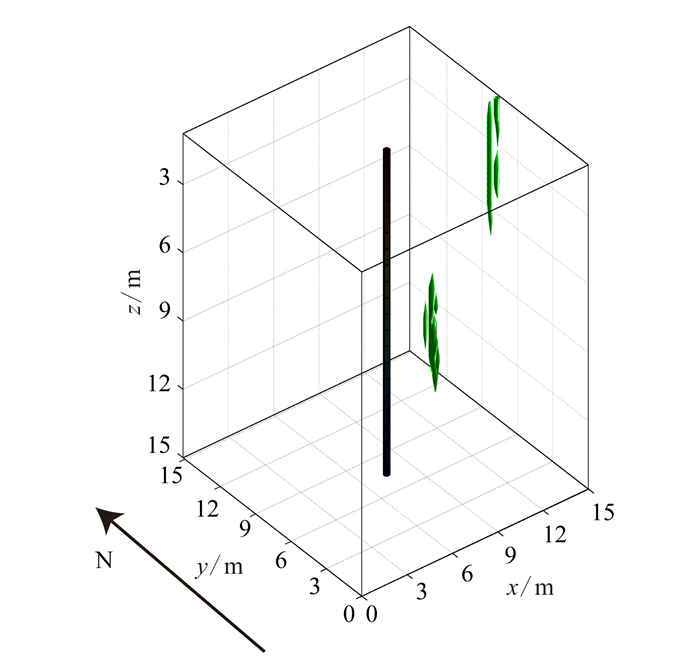
最后,利用所求的方位角进行三维成像显示,结果如图 10所示。从图 10可以清楚看出,在井的正东方向存在一个异常,与原模型正东方向的裂缝吻合良好;在井的正南方向同样存在一个异常,与原模型正南方向的裂缝吻合良好。考虑到定向钻孔雷达是从井底向井口运行的,残差法算法只能识别裂缝在竖直方向上的规模,类似地面物探中的二维测量。如果有一排钻孔,就能看出水平向变化。综上所述,残差法在该模型中取得了非常好的应用。
|
| 图 10 模型的三维成像结果 Figure 10 Three-dimensional imaging results |
|
|
1) 本文研究的定向钻孔雷达包含1个发射天线和4个接收天线,通过所接收到波形到达的先后次序,可以有效地确定目标地质体的精确方位。
2) 本文实现了对残差法的算法改进,成功实现了残差法对于多目标的方位识别,并在此基础上提出并实现了钻孔雷达纵横切片以及三维成像方法。
3) 利用GprMax合成数据,检验改进算法的适用性,可以看出改进后残差法可以有效判断目标地质体的精确方位,并且在三维成像中取得了非常好的效果。
| [1] |
曾昭发, 李文奔, 习建军, 等. 基于DOA估计的阵列式探地雷达逆向投影目标成像方法[J].
吉林大学学报(地球科学版), 2017, 47(4): 1308-1318.
Zeng Zhaofa, Li Wenben, Xi Jianjun, et al. Inverse Direction Imaging Method of Array Type GPR Based on DOA Estimation[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(4): 1308-1318. |
| [2] | Sato M, Takayama T. A Novel Directional Borehole Radar System Using Optical Electric Field Sensors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(8): 2529-2535. DOI:10.1109/TGRS.2007.898421 |
| [3] | Lytle R J, Laine E F. Design of Miniature Directional Antenna for Geophysical Probing from Borehole[J]. IEEE Transactions on Geoscience and Remote Sensing, 1978, 16(6): 304-307. |
| [4] |
朱自强, 彭凌星, 鲁光银, 等. 基于互相关函数对钻孔雷达层析成像的改进[J].
吉林大学学报(地球科学版), 2014, 44(2): 668-674.
Zhu Ziqiang, Peng Lingxing, Lu Guangyin, et al. Improved Borehole-GPR Tomography Based on Cross-Correlation[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(2): 668-674. |
| [5] |
张理轻, 马晔, 杨宇, 等. 钻孔雷达数据处理技术及分析[J].
地震工程学报, 2014, 36(4): 1107-1112.
Zhang Liqing, Ma Ye, Yang Yu, et al. Study on Data Processing Techniques of Borehole Radar[J]. China Earthquake Engineering Journal, 2014, 36(4): 1107-1112. |
| [6] | Lytle R J, Laine E F. Design of Miniature Directional Antenna for Geophysical Probing from Borehole[J]. IEEE Transactions on Geoscience and Remote Sensing, 1978, 16(6): 304-307. |
| [7] | Olsson O, Falk L, Forslund O, et al. Borehole Radar Applied to the Characterization of Hydraulic Conductive Fracture Zones in Crystalline Rock[J]. Geophysical Prospecting, 2010, 40(2): 109-142. |
| [8] |
陈建胜, 陈从新. 钻孔雷达技术的发展和现状[J].
地球物理学进展, 2008, 23(5): 300-306.
Chen Jiansheng, Chen Congxin. The Review of Borehole Radar Technology[J]. Progress in Geophysics, 2008, 23(5): 300-306. |
| [9] | Sato M, Ohkubo T, Niitsuma H. Cross-Polarimetric Borehole Radar Measurement with a Slot Antenna[J]. Journal of Applied Geophysics, 1995, 33(1): 53-61. |
| [10] | Ebihara S, Sasakura A. Mode Effect on Direct Wave in Single-Hole Borehole Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2): 854-867. DOI:10.1109/TGRS.2010.2057437 |
| [11] | Falk L R, Olsson O L, Sandberg E V. Combined Interpretation of Fracture Zones in Crystalline Rock Using Single-Hole, Crosshole Tomography and Directional Borehole-Radar Data[J]. Society of Petrophysicists and Well-Log Analysts, 1991, 32(2): 12. |
| [12] |
曾昭发, 刘四新, 王者江, 等.
探地雷达方法原理及应用[M]. 北京: 科学出版社, 2006.
Zeng Zhaofa, Liu Sixin, Wang Zhejiang, et al. Ground Penetrating Radar Method and Application[M]. Beijing: Beijing Science Press, 2006. |
| [13] | Ebihara S. Super-Resolution of Coherent Targets by a Directional Borehole Radar[J]. IEEE Transactions on Geoscience & Remote Sensing, 2000, 38(4): 1725-1732. |
| [14] | Takayama T, Sato M. A Novel Direction-Finding Algorithm for Directional Borehole Radar[J]. IEEE Transactions on Geoscience & Remote Sensing, 2007, 45(8): 2520-2528. |
| [15] | Ebihara S, Kawai H, Wada K. Estimating the 3D Position and Inclination of a Planar Interface with a Directional Borehole Radar[J]. Near Surface Geophysics, 2013, 11(2): 185-195. |
| [16] | Giannopoulos A. Modelling Ground Penetrating Ra-dar by GprMax[J]. Construction & Building Materials, 2005, 19: 755-762. |



