0 引言
在位场数据的处理中,垂向导数可以压制区域场、圈定局部场[1]、分离水平叠加异常。并且在位场其他处理方法中,垂向导数的求取也至关重要,例如欧拉反褶积、向下延拓[2]、重力归一化梯度等常规位场数据处理方法中都需要先进行垂向导数的计算。可见导数换算作为处理过程的重要组成部分,其结果的好坏直接影响到这些位场数据处理方法的计算精度。位场垂向导数的换算方法可以分为:空间域法和波数域法。空间域法包括有限元法[3]、样条函数法[4-6]等;波数域法包括常规FFT算子、维纳滤波法[7]、补偿圆滑滤波法[8]、正则化方法[9]、新正则化方法[10]及波数域迭代法[11]。其他方法包括Fedi等[12]提出的ISDV算法,该方法在空间域与波数域相结合换算出垂向导数。目前,ISVD算法已经成为稳定求解位场各阶垂向导数的重要方法,并广泛应用到位场的数据处理中[13-15]。
由于空间域的算法普遍存在计算速度慢等缺点,因此目前常在频率域对位场的高阶垂向导数进行计算;但是频率域的导数响应因子具有高频放大作用,当所求导数的阶数越高,数据对噪声的敏感程度就越大,导致所求结果不稳定。为了压制高阶导数计算结果的不稳定性,本文提出一种基于Tikhonov正则化迭代法计算位场各阶垂向导数的方法,并通过模型试验及实际数据的应用,对该方法计算垂向导数的稳定性进行了验证。
1 方法原理位场T(x, y)与其各阶垂向导数Dm(x, y)(m代表阶数)在波数域的关系式为
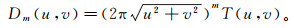 (1)
(1) 式中:Dm(u, v)和T(u, v)分别为Dm(x, y)和T(x, y)傅里叶变换的频谱结果;u和v分别为x和y方向的波数;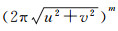
针对式(1)的不稳定问题,Tikhonov正则化是一种广泛应用的方法,即求解一个极小化的正则化泛函:
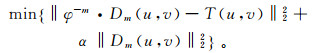 (2)
(2) 其中:‖ ‖2表示L2范数;α为正则化参数,用于平衡不稳定性及光滑性。上述极小化问题的解为
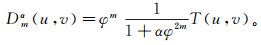 (3)
(3) 其中,Dmα(u, v)表示正则垂向导数换算结果。由式(3)可见,Tikhonov正则垂向导数换算算子可分为2部分:常规垂向导数换算算子部分φm和Tikhonov正则低通滤波函数部分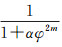
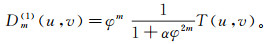 (4)
(4) 将Dm(1)(u, v)代入到式(1)中,得T的一阶近似谱:
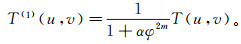 (5)
(5) 再用T(u, v)和T(1)(u, v)对Dm(1)(u, v)进行矫正,得Dm(u, v)的二阶近似谱:
 (6)
(6) 重复以上步骤,得Dm(u, v)的n阶近似谱:
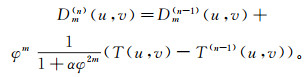 (7)
(7) 由式(1)可知:
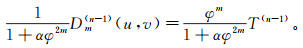 (8)
(8) 代入式(7)得:
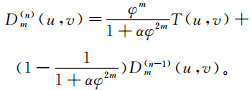 (9)
(9) 由数学归纳法很容易得到迭代通式:
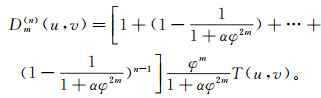 (10)
(10) 显然式(10)右端中括号内为一等比数列,其公比0≤ 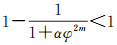
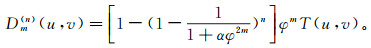 (11)
(11) 当迭代无穷大时,
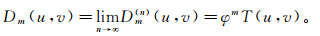 (12)
(12) 上式表明,本文提出的Tikhonov正则化迭代法进行高阶导数换算是可以收敛到理论解的。其中正则化参数α的常用取值范围为(0.001,1),迭代次数在10以内即可。
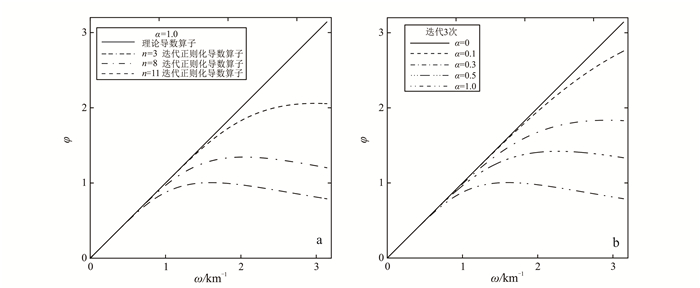
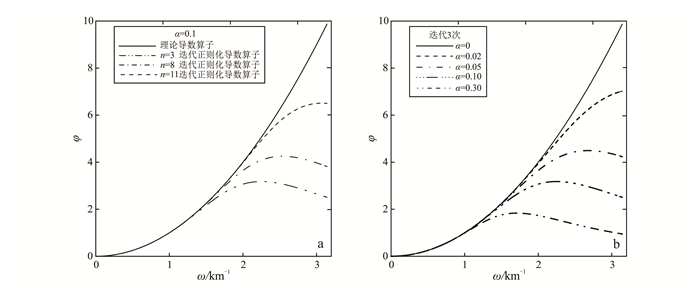
2 滤波特性分析图 1和图 2分别是垂向一阶导数和垂向二阶导数的Tikhonov正则化迭代算子滤波特性。其中,图 1a和图 2a分别是不同迭代次数的垂向一阶导数和垂向二阶导数Tikhonov正则化迭代算子的滤波响应特征曲线。其中,横坐标ω为径向圆频率,数据的点距均为1 km,垂向一阶导数的正则化参数α的取值为1.0,垂向二阶导数的正则化参数α的取值为0.1。对理论垂向导数算子φm、Tikhonov正则化迭代法垂向导数换算算子的滤波特性进行对比分析可得:理论垂向导数因子φm随着频率的增加急剧上升,且导数阶次越高,高频成分被放大得越强;Tikhonov正则化迭代算子在低频段逼近理论垂向导数算子,保证了低频有用信号处导数的换算,在高频阶段却能对其进行压制;随着迭代次数的增加,Tikhonov正则化迭代算子逐渐趋近于理论垂向导数算子。为了分析正则化参数α的取值对Tikhonov正则化迭代算子滤波特性的影响,图 1b和图 2b分别为迭代3次时,垂向一阶和二阶导数Tikhonov正则化迭代算子的滤波响应特征曲线。可以看出:当迭代次数不变时,随着导数阶次的增加,Tikhonov正则化迭代算子对高频成分的压制作用逐渐增强,保证了高阶导数换算的稳定性;正则化参数α取值越小,Tikhonov正则化迭代算子在高频段的压制作用越弱,当其值为0时,则结果为理论导数算子;当正则化参数α的取值过大时,对低频段也产生一定的压制作用,则会影响滤波效果。
|
| a.α=1.0,不同迭代次数;b.迭代3次,不同α取值。ω为径向圆频率。 图 1 垂向一阶导数的Tikhonov正则化迭代算子滤波特性 Figure 1 Filtering properties of vertical derivative with Tikhonov regularization iteration factor |
|
|
|
| a.α=0.1,不同迭代次数;b.迭代3次,不同α取值。 图 2 垂向二阶导数的Tikhonov正则化迭代算子滤波特性 Figure 2 Filtering properties of second vertical derivative with Tikhonov regularization iteration factor |
|
|
可见,本文提出的Tikhonov正则化迭代算子在低频段能精确地逼近理论导数算子,对高频成分则能有效压制,因而该方法在理论上具有保幅性和稳定性的优点。
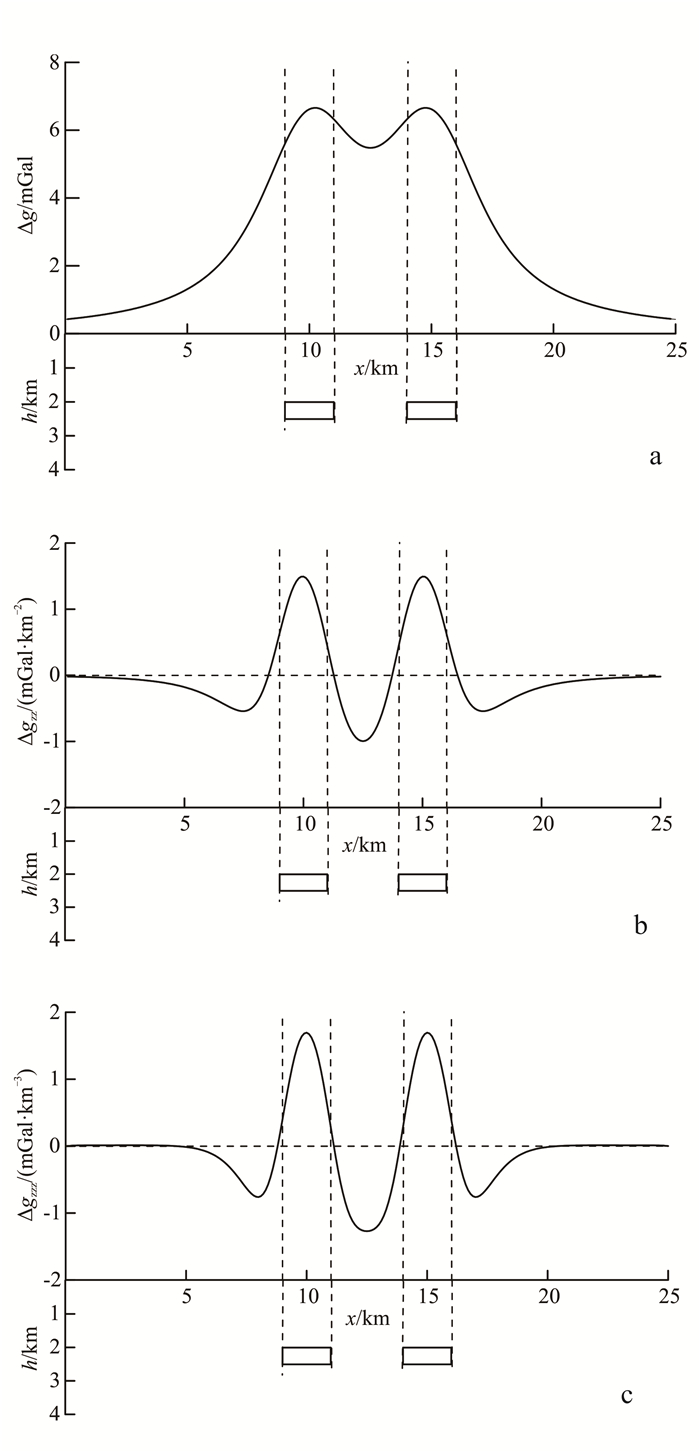
3 模型试验文中采用2个二度直立柱体的叠加异常进行数值检验。模型体1和2长均为2.0 km,上顶埋深h为2.0 km,下底埋深h为2.5 km; 其中心位置x分别为10、15 km,点距为0.1 km,2个模型体的剩余密度均为1.0 g/cm3。组合模型体相对位置及其产生的重力异常Δg如图 3a所示,图 3b和图 3c分别是无噪声情况下理论的垂向二阶导数和垂向三阶导数。添加重力异常幅值0.1%的随机噪声,图 4和图 5分别是含噪声情况下常规FFT法和Tikhonov正则化迭代法所计算出的垂向二阶以及垂向三阶导数。其中,二阶垂向导数的正则化参数为0.1,迭代8次;垂向三阶导数的正则化参数为0.5,迭代8次。
|
| 图 3 模型重力异常及模型位置(a)、垂向二阶导数(b)和垂向三阶导数(c) Figure 3 Gravity anomaly and the position of the model (a), the second vertical derivative (b) and the third vertical derivative (c) |
|
|
|
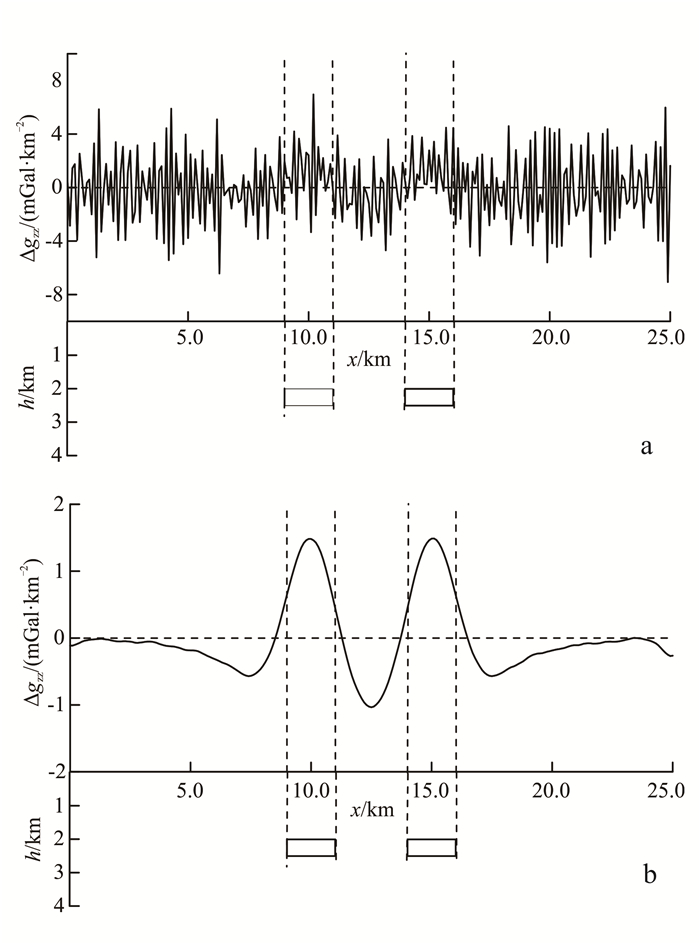
| 图 4 FFT垂向二阶导数(a)和Tikhonov正则化迭代法垂向二阶导数(b) Figure 4 Second vertical derivative using FFT method (a) and the second vertical derivative using Tikhonov regularization iteration method (b) |
|
|

|
| 图 5 常规FFT垂向三阶导数(a)和Tikhonov正则化迭代法垂向三阶导数(b) Figure 5 Third vertical derivative using FFT method (a) and the third vertical derivative using Tikhonov regularization iteration method (b) |
|
|
图 4和图 5分别是常规FFT法和Tikhonov正则化迭代法计算垂向二阶和三阶导数的对比图。从图中可以看出,由于噪声的干扰,用常规FFT变换计算的垂向导数结果存在着明显的波动性,且导数的阶次越高,稳定性越差,无法识别有效异常,这是由于理论导数算子对高频成分的放大作用。Tikhonov正则化迭代法计算垂向二阶及三阶导数结果稳定,对噪声的压制能力强,这是因为正则化迭代法的滤波特性,在低频段较好地逼近理论因子,而在高频段可以较好地压制噪声。对比图 3b和3c中不含噪声计算得到的垂向二阶导数和三阶导数可以看出,随着求导次数的增加,高频部分的影响越来越大,即图 3c中曲线的震荡幅度大于图 3b中。从图 4b和图 5b可以看出,Tikhonov正则化迭代法计算得到的导数,在数量级上和换算得到的导数(图 3b和3c)数量级是相同的,垂向三阶导数的结果图中并没有出现明显的震荡,再次说明了Tikhonov正则化迭代法的准确性和稳定性。图 4b模型体1和2中,零值点对应的横坐标分别为8.5和11.3、13.7和16.5,图 5b模型体1和2中,零值点对应的横坐标分别为8.6和11.2、13.8和16.4,可以看出,随着所计算导数的阶次增加,曲线的零值点位置与地质体边界的对应效果越来越好。
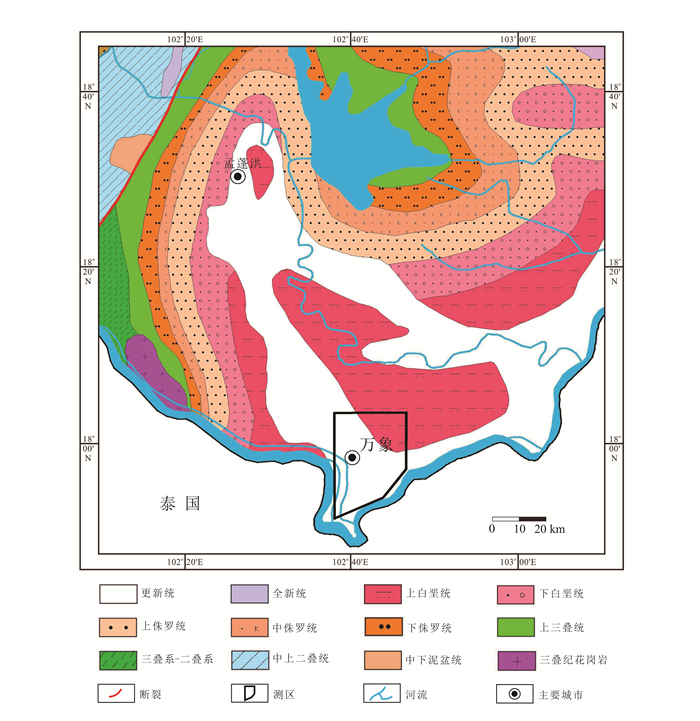
4 实际应用为了试验Tikhonov正则化迭代法求垂向导数对实际资料的处理效果,我们对老挝万象盆地的布格重力异常Δg数据进行垂向二阶导数的计算,其中,实际数据的点距为0.2 km。该研究区的地质情况复杂,如图 6。图 7a为该研究区的布格重力异常,比例尺为1:50 000,局部细化为1:25 000。
|
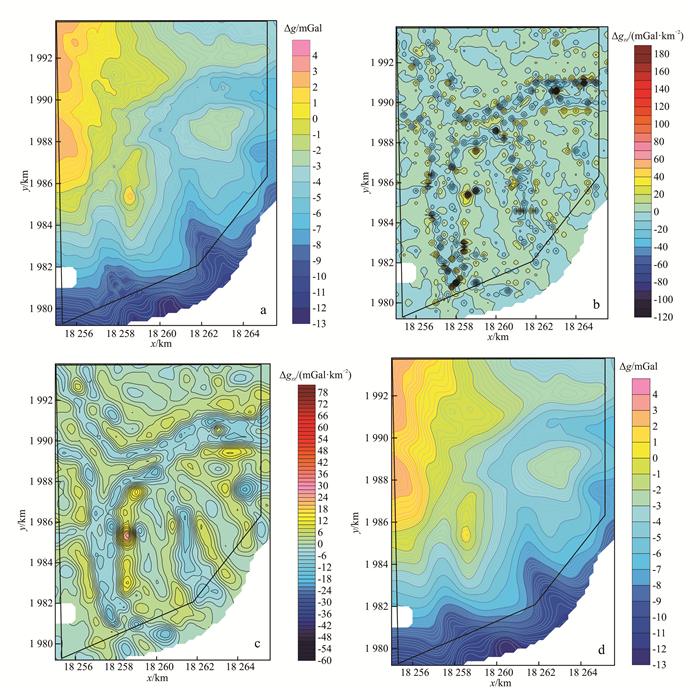
| 图 7 原始重力异常(a)、常规FFT法垂向二阶导数(b)、Tikhonov正则化迭代法得到的垂向二阶导数(c)及垂向二次积分得到的重力异常(d) Figure 7 Original gravity anomaly (a), the second vertical derivative using FFT (b), the second vertical derivative using Tikhonov regularization iteration method (c) and the gravity anomaly result by the secondary vertical integration (d) |
|
|
从图 7b中可以看出,由于研究区数据中噪声的干扰,常规FFT法得到的垂向二阶导数结果稳定性差,单点异常多且杂乱,几乎不能从中看出研究区的浅部异常特征;图 7c为Tikhonov正则化迭代法对该研究区的垂向二阶导数计算结果,其中,正则化参数α为0.001,迭代5次。从图 7c中可以看出Tikhonov正则化迭代法计算结果稳定,噪声得到了有效压制,研究区的浅部异常清晰明显、连续性高,这有利于对研究区断裂的划分以及成矿远景区的预测。
为了验证Tikhonov正则化迭代法计算的垂向二阶导数结果,我们对图 7c进行二次积分,得到了通过重力垂向二阶导数计算出的重力异常图 7d。通过对原始重力异常图 7a以及积分计算出的重力异常图 7d对比可以看出,计算所得重力异常和原始重力异常在形态与数值上吻合得非常好,说明该方法对垂向二阶导数的计算精度高。
5 结论1) 本文将Tikhonov正则化与迭代法相结合,提出一种计算位场高阶导数的新方法,通过分析该算子的滤波特性,表明该方法具有一定的稳定性及保幅性。
2) 通过模型试验也可以看出,该方法计算出的高阶导数比常规FFT求导法更稳定,因此对异常体边界的识别效果更好。Tikhonov正则化迭代法对实际数据的处理结果说明了该方法较常规FFT求导法有更高的稳定性和实用价值。
3) 该方法的提出可以为实际数据的处理提供一种参考,提高后续异常解释的准确性。
| [1] |
肖锋, 吴燕冈, 孟令顺. 重力异常图中的边界增强和提取技术[J].
吉林大学学报(地球科学版), 2011, 41(4): 1197-1203.
Xiao Feng, Wu Yangang, Meng Lingshun. Edge Enhancement and Detection Technology in Gravity Anomaly Map[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(4): 1197-1203. |
| [2] |
张冲, 黄大年, 秦朋波, 等. 重力场向下延拓的三阶Adams-Bashforth公式法[J].
吉林大学学报(地球科学版), 2017, 47(5): 1533-1542.
Zhang Chong, Huang Danian, Qin Pengbo, et al. Third-Order Adams-Bashforth Formula Method for Downward Continuation of Gravity Field[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(5): 1533-1542. |
| [3] |
徐世浙. 用边界单元法计算任意形体的重力异常及其导数[J].
石油物探, 1984, 23(2): 22-37.
Xu Shizhe. The Calculation of the Gravitational Anomaly and Its Derivative of the Geologic Body with Arbitrary Configuration by Boundary-Elements Method[J]. Geophysical Prospecting for Petroleum, 1984, 23(2): 22-37. |
| [4] |
汪炳柱. 用样条函数法求重力异常二阶垂向导数和向上延拓计算[J].
石油地球物理勘探, 1996, 31(3): 415-422.
Wang Bingzhu. Computing the Vertical Second Derivative and Upward Continuation of Gravity Anomaly by Spline Function Method[J]. Oil Geophysical Prospecting, 1996, 31(3): 415-422. |
| [5] |
姚长利, 黄卫宁, 管志宁. 综合利用位场及其垂直梯度的快速样条曲化平方法[J].
石油地球物理勘探, 1997, 32(2): 229-236.
Yao Changli, Huang Weining, Guan Zhining. Fast Splines Conversion of Curvedsurface Potential Field and Vertical Gradient Data into Horizontal-Plane Data[J]. Oil Geophysical Prospecting, 1997, 32(2): 229-236. |
| [6] | Wang B, Krebes E S, Ravat D. High-Precision Poten-tial-Field and Gradient-Component Transformations and Derivative Computations Using Cubic B-Splines[J]. Geophysics, 2008, 73(5): 135-142. DOI:10.1190/1.2952623 |
| [7] | Clarke G K C. Optimum Second-Derivative and Down-ward-Continuation Filters[J]. Geophysics, 1969, 34(3): 424-437. DOI:10.1190/1.1440020 |
| [8] |
侯重初. 补偿圆滑滤波方法[J].
石油物探, 1981, 20(2): 22-29.
Hou Zhongchu. Filtering of Smooth Compensation[J]. Geophysical Prospecting for Petroleum, 1981, 20(2): 22-29. |
| [9] | Pašteka R, Richter F P, Karcol R, et al. Regularized Derivatives of Potential Fields and Their Role in Semi-Automated Interpretation Methods[J]. Geophysical Prospecting, 2009, 57(4): 507-516. DOI:10.1111/gpr.2009.57.issue-4 |
| [10] |
曾小牛, 李夕海, 贾维敏, 等. 位场各阶垂向导数换算的新正则化方法[J].
地球物理学报, 2015, 58(4): 1400-1410.
Zeng Xiaoniu, Li Xihai, Jia Weimin, et al. A New Regularization Method for Calculating the Vertical Derivatives of the Potential Field[J]. Chinese Journal of Geophysics, 2015, 58(4): 1400-1410. DOI:10.6038/cjg20150426 |
| [11] |
王彦国, 张瑾. 位场高阶导数的波数域迭代法[J].
物探与化探, 2016, 40(1): 143-147.
Wang Yanguo, Zhang Jin. The Iterative Method for Higher-Order Derivative Calculation of Potential Fields in Wave Number Domain[J]. Geophysical and Geochemical Exploration, 2016, 40(1): 143-147. |
| [12] | Fedi M, Florio G. Detection of Potential Fields Sou-rce Boundaries by Enhanced Horizontal Derivative Method[J]. Geophysical Prospecting, 2001, 49(1): 40-58. DOI:10.1046/j.1365-2478.2001.00235.x |
| [13] | Fedi M, Florio G. A Stable Downward Continuation by Using the ISVD Method[J]. Geophysical Journal International, 2002, 151(1): 146-156. DOI:10.1046/j.1365-246X.2002.01767.x |
| [14] | Cooper G R J, Cowan D R. Filtering Using Variable Order Vertical Derivatives[J]. Computers & Geosciences, 2004, 30(5): 455-459. |
| [15] |
卞光浪, 翟国君, 高金耀, 等. 总强度磁场稳健向下延拓的改进泰勒级数法[J].
测绘学报, 2014, 43(1): 30-36.
Bian Guanglang, Zhai Guojun, Gao Jinyao, et al. Improved Taylor Series Approach for Stable Downward Continuation of Total Strength of Geomagnetic Field[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 30-36. |
| [16] | Xu M L, Yang C B, Wu Y G, et al. Edge Detection in the Potential Field Using the Correlation Coefficients of Multidirectional Standard Deviations[J]. Applied Geophysics, 2015, 12: 23-34. DOI:10.1007/s11770-014-0473-5 |