0 引言
随着地震勘探区域复杂性的加大,为了适应复杂地区速度的剧烈变化,偏移技术从叠前时间偏移发展到了叠前深度偏移。叠前深度偏移能够真正实现共成像点叠加,在陡倾角和横向速度变化剧烈地区比叠前时间偏移的成像精度更高[1-3]。
目前叠前深度偏移方法主要有Kirchhoff积分法、有限差分法和傅里叶变换法。有限差分法叠前深度偏移尽管偏移精度高,但是它过度依赖速度场,对陡倾角的成像精度不高,不适应低信噪比和非规则数据的地震资料,计算效率低;傅里叶变换法叠前深度偏移算法精度较高,没有频散现象的发生,但是它不能适应横向速度的剧烈变化,因而在地震勘探中没有得到广泛应用。相对于前两种方法,Kirchhoff积分法叠前深度偏移方法能够适应横向速度的剧烈变化,对陡倾角具有很好的成像精度,能够较好地适应低信噪比、非规则的地震数据,具有很高的计算效率,因此在地震勘探中得到了广泛应用[4-7]。
Kirchhoff积分法叠前深度偏移方法由两部分完成:旅行时的计算和积分计算,该方法的偏移精度主要围绕提高旅行时的计算精度。基于模型约束的Kirchhoff积分法叠前深度偏移方法在常规建模的基础上,通过加入目标地质体的层位约束求取加入层位约束前后两个旅行时的差来优化模型,比传统建模方式进一步减小旅行时的误差,从而提高偏移算法的成像精度,得到了很好的效果[8-14]。
本文对基于模型约束的Kirchhoff积分法叠前深度偏移方法从原理上进行阐述,利用正演模拟数据验证方法的准确性,并对原始地震数据进行试处理。
1 Kirchhoff积分法叠前深度偏移基本原理Kirchhoff积分法叠前深度偏移成像技术是20世纪90年代随着地震勘探技术的发展而成熟起来的地震波成像,在墨西哥湾和北海地区得到成功应用[15],能够适用于盐丘、潜山、逆掩推覆构造和高陡构造等复杂构造地区成像精度的要求。
Kirchhoff积分法叠前深度偏移的理论基础是求解波动方程的格林函数,通过格林函数建立地下波场和反射波的积分关系,根据成像约束关系实现地震波偏移归位。它的实现过程可分为两步:模型建立和偏移归位。Kirchhoff积分法叠前深度偏移的公式[16]为
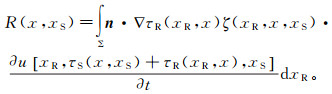 (1)
(1) 式中:R(x, xS)是反射系数;n是反射面Σ的外法线方向向量;xS、xR、x分别表示激发点、接收点、成像点;τS、τR分别表示激发点到成像点和成像点到接收点的旅行时;ζ(xR, x, xS)是波场扩散因子;∂u[xR, τS(x, xS)+τR(xR, x), xS]是地震波在介质中传播的位移。
2 模型建立、优化及测试 2.1 模型建立深度偏移模型建立的好坏直接决定叠前深度偏移成像的结果。目前,基于射线追踪的层析速度反演方法是叠前深度偏移成像的关键建模技术之一,它主要利用归位和层析迭代进行速度反演,用来恢复速度场中的高、低频信息,在工业界广泛用于建立速度模型。
层析速度反演过程包括建模和模型更新过程。首先对模型进行网格化,对网格中的每个反射点进行射线追踪,每条射线路径可以用一个等式来表示,整个模型的射线路径[17]可以表示为
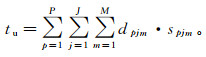 (2)
(2) 式中:P、J、M为网格点数;tu为地震波旅行时;dpjm为模型中第pjm网格点的射线路径长度;spjm为模型中第pjm网格点的慢度。则旅行时差为
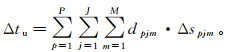 (3)
(3) 式中:Δtu为地震波的旅行时差;Δspjm为模型中第pjm网格点的慢度误差。通过求得旅行时差Δtu更新速度模型可以实现层析速度模型的迭代。
2.2 模型优化常规Kirchhoff积分法叠前深度偏移只是根据速度场建立模型直接求取旅行时差更新模型来进行深度偏移;而基于模型约束的Kirchhoff积分法叠前深度偏移是在常规深度偏移建模基础上加入了目标地质体层位的约束,通过层位约束可以有效地提高模型更新的精度,从而更好地提高Kirchhoff积分法叠前深度偏移成像的准确性和分辨率。
模型约束的Kirchhoff积分法叠前深度偏移解决的主要问题是减小层析速度迭代的旅行时差。层析速度建模反演是一个多解性问题,为了降低这种多解性,可以在反演迭代过程中加入已知地质层位的约束,例如准确地质层位的网格速度等[18]。
公式(3)可以改写为
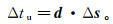 (4)
(4) 式中:d是dpjm表示的系数矩阵;Δs为变量Δspjm的向量。
对于已知的网格速度,可以通过正则化加入这种特定的约束,并加入准确地质层位的网格速度。则公式(4)可以表示为
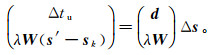 (5)
(5) 式中:s′为准确地质层位的网格速度慢度向量;sk为模型第k次迭代解;W为L×N维矩阵,Wi=[0…1…0],i∈[1, L],表示被约束的参数为1,其他参数为0;λ为正则化因子。方程组(5)可以用正交分解最小二乘法(LSQR)进行求解。
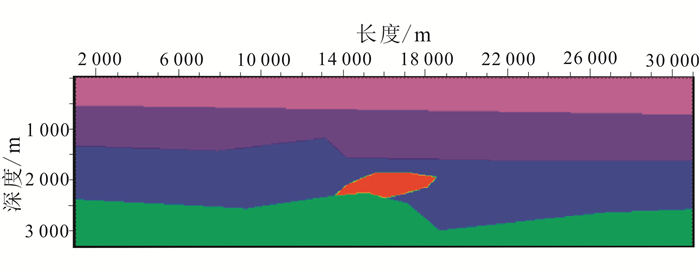
2.3 模型测试建立如图 1所示的模型,并对基于模型约束的Kirchhoff积分法叠前深度偏移方法进行测试。图 1模型长30 000 m,深3 300 m,由上至下依次有4层介质,第三层介质中有一个近似椭圆形的介质;4层介质的速度依次为:3 870、4 430、4 480、4 590 m/s,椭圆形介质速度为4 340 m/s。对该模型进行纵向、横向均为20 m×20 m的网格离散化,设计理论炮点500炮,中间激发,炮点距60 m,接收道数600道,道间距20 m,最大偏移距6 000 m,采样间隔4 ms。
|
| 图 1 模型示意图 Figure 1 Model schematic diagram |
|
|
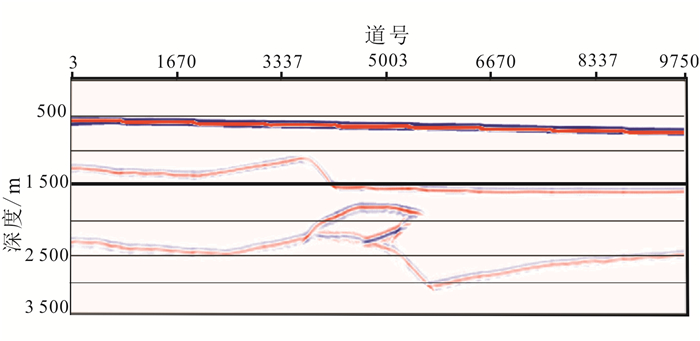
图 2是利用基于模型约束的Kirchhoff积分法叠前深度偏移方法对图 1模型正演得到的数据进行叠前深度偏移的结果。可以看出,偏移结果与模型结构形态吻合,验证了该方法的准确性。
|
| 图 2 叠前深度偏移成像图 Figure 2 Diagram of pre-stack migration in the depth domain |
|
|
应用基于模型约束的Kirchhoff积分法叠前深度偏移方法对某地区海洋三维地震数据进行测试。以海水和沉积岩速度体作为初始速度反演模型,以沉积岩中盐丘速度体作为已知层位约束,通过式(5)对初始速度反演模型进行优化,用优化后的速度模型进行Kirchhoff积分法叠前深度偏移成像。
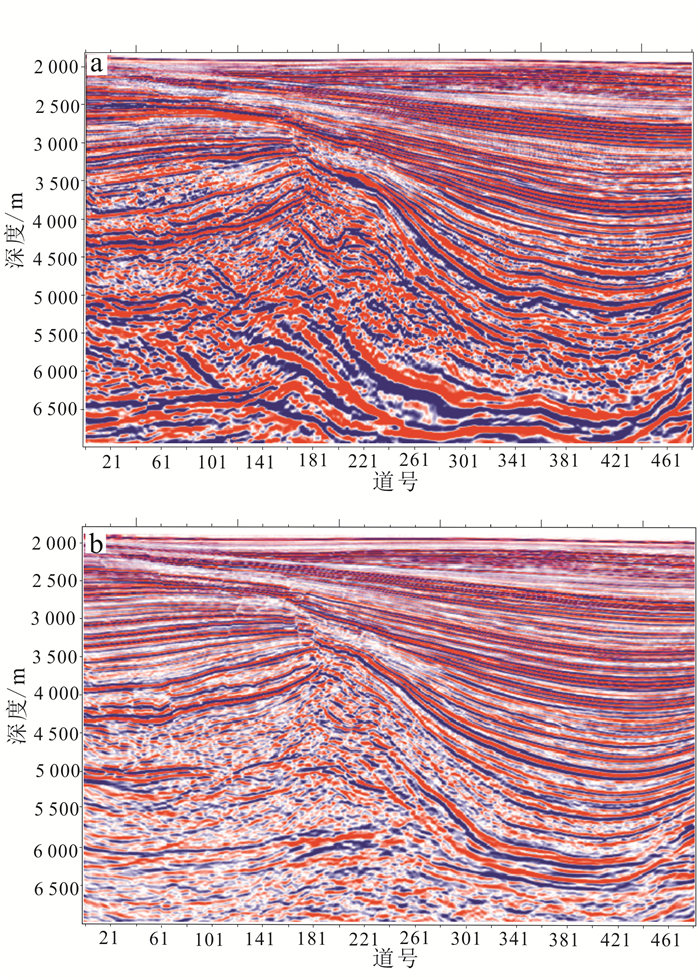
叠前时间偏移与叠前深度偏移成像结果的对比如图 3所示。叠前时间偏移成像结果在盐丘边界和内部区域反射比较杂乱,边界不清,信噪比较低(图 3a);优化模型约束的Kirchhoff积分法叠前深度偏移成像结果整体信噪比较高,断点干脆,盐丘与围岩接触边界清楚,盐丘底部成像清晰可见,波组特征能够连续追踪(图 3b)。
|
| 主测线号:1700。 图 3 叠前时间偏移(a)和叠前深度偏移(b)对比图 Figure 3 Diagram of pre-stack migration in the time domain (a) and pre-stack migration in the depth domain (b) |
|
|
对比叠前时间偏移和叠前深度偏移成像结果,基于模型约束的Kirchhoff积分法叠前深度偏移方法能够解决横向速度剧烈变化带来的偏移成像不精确的技术难点,有效地提高了地震波成像的信噪比和分辨率,较好地解决了高速盐丘底部成像问题,波组特征明显,为深部探测成像提供了有效的技术方法。
| [1] |
张猛, 孟祥宾, 匡斌, 等. 积分法叠前深度偏移技术在BS6地区的应用[J].
勘探地球物理进展, 2009, 32(1): 48-54.
Zhang Meng, Meng Xiangbin, Kuang Bin, et al. Application of Prestack Depth Migration Techniques of STseis Software System in BS6 Area[J]. Progress in Exploration Geophysics, 2009, 32(1): 48-54. |
| [2] | Hagedoorn J G. A Process of Seismic Reflection Inter-pretation[J]. Geophysical Prospecting, 1954, 2(2): 85-127. DOI:10.1111/gpr.1954.2.issue-2 |
| [3] |
杨晓东, 秦宁, 王延光. 常用叠前深度偏移方法特点分析与实例对比[J].
地球物理学进展, 2015, 30(2): 740-745.
Yang Xiaodong, Qin Ning, Wang Yanguang. Analysis and Examples of Commonly Used Prestack Depth Migration Methods[J]. Progress in Geophysics, 2015, 30(2): 740-745. DOI:10.6038/pg20150235 |
| [4] |
王华忠, 李伟波, 张元巧. 起伏地表条件下偏移到多偏移距叠前时间偏移[J].
勘探地球物理进展, 2007, 30(5): 361-367.
Wang Huazhong, Li Weibo, Zhang Yuanqiao. Prestack Noise Suppression with Ray-Beam Gather Stacking[J]. Progress in Exploration Geophysics, 2007, 30(5): 361-367. |
| [5] |
程玖兵, 王楠, 马在田. 表驱三维角度域Kirchhoff叠前时间偏移成像方法[J].
地球物理学报, 2009, 52(3): 792-800.
Cheng Jiubing, Wang Nan, Ma Zaitian. Table-Driven 3-D Angle-Domain Imaging Approach for Kirchhoff Prestack Time Migration[J]. Chinese Journal of Geophysics, 2009, 52(3): 792-800. |
| [6] |
周东红, 张志军. 基于三维模型数据的Kirchhoff叠前时间偏移保幅性分析[J].
地球物理学进展, 2016, 31(5): 2292-2298.
Zhou Donghong, Zhang Zhijun. Analysis of the Amplitude Preservation of Kirchhoff Prestack Time Migration Method Based on 3D Model Data[J]. Progress in Geophysics, 2016, 31(5): 2292-2298. DOI:10.6038/pg20160556 |
| [7] |
王征, 杨锴, 董水利, 等. 应用叠前时间偏移/反偏移与CRS-OIS叠加削弱倾角歧视影响[J].
石油地球物理勘探, 2015, 50(5): 839-847.
Wang Zheng, Yang Kai, Dong Shuili, et al. Dip Discrimination Reduction with CRS-OIS[J]. Oil Geophysical Prospecting, 2015, 50(5): 839-847. |
| [8] |
董臣强, 谭明友, 张明振, 等. Kirchhoff积分法叠前深度偏移技术在孤岛地区的应用[J].
石油地球物理勘探, 2002, 37(2): 180-184.
Dong Chenqiang, Tan Mingyou, Zhang Mingzhen, et al. Application of Prestack Depth Migration in Gudao Area by Kirchhoff Integration[J]. Oil Geophysical Prospecting, 2002, 37(2): 180-184. |
| [9] | Luděk Klimeš. Resolution of Prestack Depth Migration[J]. Studia Geophysica et Geodaetica, 2012, 56(2): 457-482. DOI:10.1007/s11200-011-9014-8 |
| [10] |
李振春. 地震偏移成像技术研究现状与发展趋势[J].
石油地球物理勘探, 2014, 49(1): 1-21.
Li Zhenchun. Research Status and Development Trends for Seismic Migration[J]. Oil Geophysical Prospecting, 2014, 49(1): 1-21. |
| [11] |
张建伟. 变速介质三维地震叠前深度域成像与应用研究[D]. 成都: 成都理工大学, 2004.
Zhang Jianwei. Research of 3-D Seismic Prestack Depth Domain Imaging in Laterally Varying Media and Application[D]. Chengdu: Chengdu University of Technology, 2004. |
| [12] | Etgen J, Gray S H, Zhang Yu. An Overview of Depth Imaging in Exploration Geophysics[J]. Geophysics, 2009, 74(6): 5-17. DOI:10.1190/1.3223188 |
| [13] | Stolt R H. Migration by Fourier Transform[J]. Geo-physics, 1978, 43: 23-48. |
| [14] |
方伍宝, 孙建国. 复杂条件下的深度成像技术[J].
石油与天然气地质, 2005, 26(6): 816-822.
Fang Wubao, Sun Jianguo. Depth Imaging Technique in Complex Conditions[J]. Oil &Gasgeology, 2005, 26(6): 816-822. DOI:10.11743/ogg20050622 |
| [15] |
马淑芳, 李振春. 波动方程叠前深度偏移方法综述[J].
勘探地球物理进展, 2006, 30(3): 153-161.
Ma Shufang, Li Zhenchun. Review of Wave Equation Prestack Depth Migration Methods[J]. PEG, 2006, 30(3): 153-161. |
| [16] |
张新培, 于雪峰. 利用地球物理信息描述太古宇潜山有效储集体[J].
吉林大学学报(地球科学版), 2016, 46(1): 270-278.
Zhang Xinpei, Yu Xuefeng. Using Geophysical Information to Describe Effective Reservoirs of Archean Buried Hill[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(1): 270-278. |
| [17] |
管文胜, 段文胜, 查明, 等. 利用基于模型的层析速度反演进行低幅度构造成像[J].
石油地球物理勘探, 2017, 52(1): 87-93.
Guan Wensheng, Duan Wensheng, Zha Ming, et al. Low-Relief Structural Imaging with Model-Based Tomographic Velocity Inversion[J]. Oil Geophysical Prospecting, 2017, 52(1): 87-93. |
| [18] |
李贺. 速度场及深度偏移方法的优化与应用[D]. 成都: 成都理工大学, 2015.
Li He. Optimization and Application of Velocity Model Building and Depth Migration Method[D]. Chengdu: Chengdu University of Technology, 2015. |



