2. 湖北大学资源环境学院, 武汉 430062;
3. 国土资源部城市土地资源监测与仿真重点实验室, 广东 深圳 518000
2. Faculty of Resources and Environment, Hubei University, Wuhan 430062, China;
3. Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Land and Resources, Shenzhen 518000, Guangdong, China
0 引言
在大数据时代下,遥感数据获取方法不断丰富,信息提取技术高速发展,单一的遥感数据处理方法已经无法满足各类遥感数据的处理需求。另一方面,高分辨率和多光谱影像的大数据量促使传统遥感图像处理方法寻求机器学习方法的辅助。同时,准确的遥感图像分类可在矿产资源开发现状调查与监测[1]等多方面发挥至关重要的作用。针对多数机器算法需要进行多次迭代,会造成过拟合与训练时间过长等问题,Hinton等[2]提出了Dropout思想,在训练期间从神经网络中随机放弃一些节点,防止出现过度适应样本,从而减低过拟合现象发生的概率;黄广斌等[3]提出极限学习机算法,用线性问题解决复杂的非线性关系,大幅度提高了算法训练速度;随后,黄广斌及其团队持续对极限学习机进行了深入的改进研究[4-7]。同时,许多国内外学者也对极限学习机进行了不断的改进与深入研究。王士同等[8]在极限学习机算法的基础上提出了多层前馈神经网络结构的最小学习机算法;邓万宇等[9]考虑到了样本值的不同会对结果造成不同等级的影响,改进了加权极限学习机算法;王杰等[10]将极限学习机与粒子群算法相结合,利用粒子群算法计算出最优权值,再赋值给极限学习机进行计算。实现高空间分辨率遥感图像高效快速分类已成为遥感图像领域的重要问题,将传统遥感图像分类处理方法与机器学习方法相结合是高空间分辨率遥感数据处理的热门研究方向。
GF-2卫星作为我国自主研发的分辨率最高的民用光学遥感卫星,有效地提升了我国卫星综合观测效能,并且使之达到国际先进水平。本文基于极限学习机理论,选取实验样本进行训练,对GF-2影像进行地物分类;并将极限学习机算法与支持向量机算法和最大似然法进行对比,以验证极限学习机算法能否取得较好的分类效果,实现对遥感影像的准确分类。
1 极限学习机分类原理为提高神经网络学习算法的学习速度,极限学习机算法将神经网络的训练问题转化为解线性方程组的问题,训练前只需设置合适的隐含层节点数和激活函数,然后为输入权值和隐含层偏差量进行随机赋值,最后引入矩阵广义逆的思想且通过最小二乘法获得输出权值。整个训练过程快速简单,无需繁琐的迭代和调整参数,且具有良好的全局搜索能力,因此极限学习机在回归、分类和预测等领域得到了广泛应用。其基本原理如下[11]。
对于N个任意不相同的样本(xi, yi)(i=1, 2, …, N):
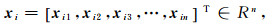 (1)
(1) 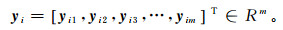 (2)
(2) 则具有L个隐神经元、激励函数为G(x)的极限学习机(extreme learning machine, ELM)输出可以表示为
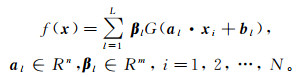 (3)
(3) 式中:al=(al1, al2, al3, …, aln)T是输入到第l个隐神经元的输入权重向量;bl是第l个隐神经元的偏置;βl=[βl1, βl2, βl3, …, βlm]是连接第l个隐神经元的输出权值;al·xi表示向量al与xi的内积。参数al、bl随机产生,本文中激励函数设置为Sigmoid函数。
如果这个含有L个隐神经元的神经网络能以零误差逼近样本(xi, yi)(i=1, 2, …, N),则存在al、bl、βl,使
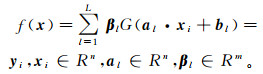 (4)
(4) 将式(4)简化为
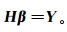 (5)
(5) 式中:β为βl组成的矩阵;Y为样本中yi组成的矩阵;H被称为隐藏层输出矩阵,即
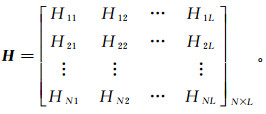 (6)
(6) 式中:H11=G(a1·x1+b1),H12=G(a2·x1+b2),H1L=G(aL·x1+bL),H21=G(a1·x2+b1),H22=G(a2·x2+b2),H2L=G(aL·x2+bL),HN1=G(a1·xN+b1),HN2=G(a2·xN+b2),HNL=G(aL·xN+bL)。
由此,输出层参数β可以由式(5)的极小2-范数最小二乘解得:
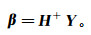 (7)
(7) 式中,H+为H的Moore-Penrose广义逆[12]。
极限学习机算法的图像分类基本流程为[13]:
1) 在图像中选取54个特征区域作为训练样本,对应54个类别,并设置激活函数G(x)及隐含层个数L。
2) 随机赋值al及bl,得到H。
3) 根据式(7)计算输出层参数β。
4) 最后将图像进行初步分类,将所得54类进行同种地物的合并,完成最终分类。
2 研究区域及遥感数据 2.1 研究数据及区域介绍本文选取吉林省长春市卡伦湖水库附近区域作为分类的研究区(图 1)。以GF-2卫星0.8 m全色及3.2 m多光谱分辨率影像作为基础数据源,将预处理后的影像重采样为1-m全色及4-m多光谱分辨率影像;基于图像特征采用scale invariant features transform算法进行图像配准[14],再通过NNDiffuse Pan Sharpening方法将两幅影像进行融合,将融合后(5 705像素×4 575像素)影像作为研究区地物分类的原始图像(图 1)。由图 1可以看出,该区域内主要为耕地,东部有大面积水域,工业仓储用地较为集中,住宅用地零散分布在耕地中,林地大致分布在水域周边及道路两旁,地物较为丰富且具有代表性。

|
| 图 1 研究区影像图 Figure 1 Image of the study area |
|
|
实验过程中,首先对分类原数据进行线性拉伸,以达到图像增强的目的;然后,根据试验区的实际地物类型,将试验区分为6类地物,按照不同地物形状、面积等特征,提取每类地物适当大小的特征区域作为训练样本。所有54个训练样本(表 1)均匀分布在研究区域内,其中水域8个,交通运输用地16个,住宅用地6个,工业仓储用地9个,耕地6个,林地9个。
| 样本名称 | 序号 | 大小(像素×像素) |
| 水域 | 1 | 51×51 |
| 2 | 12×16 | |
| 3 | 12×14 | |
| 4 | 9×10 | |
| 5 | 51×51 | |
| 6 | 51×51 | |
| 7 | 19×28 | |
| 8 | 11×29 | |
| 交通运输用地 | 1 | 31×90 |
| 2 | 14×52 | |
| 3 | 52×24 | |
| 4 | 23×17 | |
| 5 | 66×92 | |
| 6 | 54×60 | |
| 7 | 21×23 | |
| 8 | 23×25 | |
| 9 | 19×20 | |
| 10 | 28×27 | |
| 11 | 6×27 | |
| 12 | 16×7 | |
| 13 | 21×8 | |
| 14 | 16×15 | |
| 15 | 8×19 | |
| 16 | 32×35 | |
| 住宅用地 | 1 | 16×22 |
| 2 | 37×35 | |
| 3 | 26×40 | |
| 4 | 29×38 | |
| 5 | 29×43 | |
| 6 | 20×25 | |
| 工业仓储用地 | 1 | 27×81 |
| 2 | 63×64 | |
| 3 | 99×175 | |
| 4 | 71×73 | |
| 5 | 84×111 | |
| 6 | 66×82 | |
| 7 | 72×253 | |
| 8 | 103×63 | |
| 9 | 161×210 | |
| 耕地 | 1 | 51×51 |
| 2 | 51×51 | |
| 3 | 51×51 | |
| 4 | 51×51 | |
| 5 | 51×51 | |
| 6 | 26×89 | |
| 林地 | 1 | 31×37 |
| 2 | 32×49 | |
| 3 | 23×13 | |
| 4 | 37×24 | |
| 5 | 29×25 | |
| 6 | 19×16 | |
| 7 | 19×27 | |
| 8 | 22×25 | |
| 9 | 29×33 |
将水域、交通运输用地、住宅用地、工业仓储用地、耕地、林地6类样本分别采用极限学习机、支持向量机和最大似然3种监督分类方法进行图像分类,运行环境Intel(R) core(TM)i5-3 210 M,运行内存6 GB,显卡Nvidia GeForce GT 630 M,得到分类结果图,分析其分类精度及各类地物分类结果。
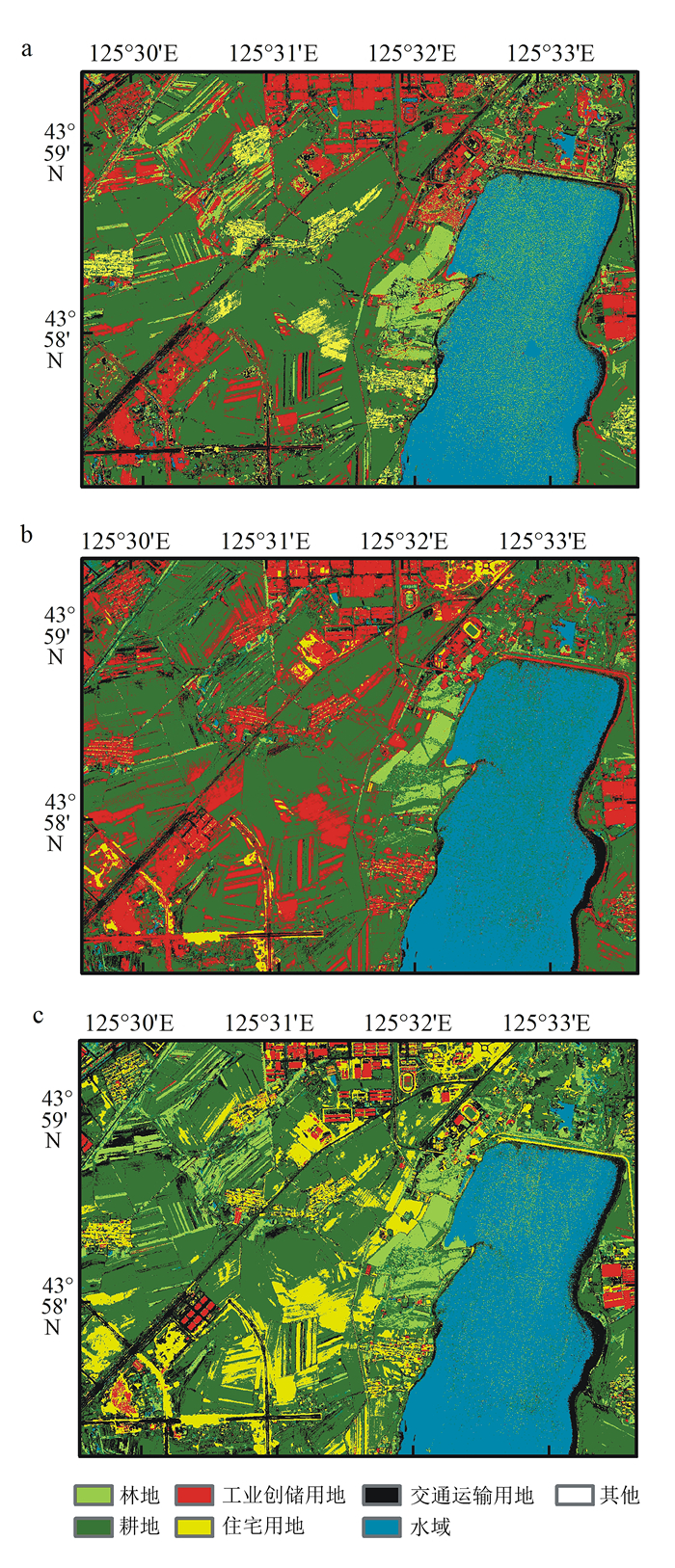
由分类结果(图 2)的正确性可以看出,极限学习机、支持向量机和最大似然3种方法均可以分类出大致的水域、交通运输用地、耕地、林地等,其中虽然存在一些错分、误分现象,但不同地物间存在明显边界,能够准确识别各类地物的位置。极限学习机分类结果(图 2a)与支持向量机分类结果(图 2b)更为相似,分类总体精度(表 2)在85%以上,kappa系数在0.7以上,说明分类结果与真实地物分类基本一致;但极限学习机分类运行时间明显优于支持向量机分类(表 2)。最大似然法分类运行时间最短,但其总体精度仅为71.552%,kappa系数为0.558,对比其他两种分类结果,其分类精度较差。
|
| a. ELM;b. SVM;c.最大似然法。 图 2 分类结果 Figure 2 Classification results |
|
|
| 分类方法 | 总体精度/% | kappa系数 | 运行时间/s |
| ELM | 85.331 | 0.718 | 310.972 |
| SVM | 86.788 | 0.737 | 2 791.614 |
| 最大似然法 | 71.552 | 0.558 | 43.040 |
由表 3可见,3种分类方法对于水域分类最为稳定,分类正确率为78.22%~84.01%;最大似然法虽总体精度较低,对于工业仓储用地的分类不如其他两种方法,但是对于交通运输用地和林地的分类明显优于其他两种方法;极限学习机分类总体精度与支持向量机相差较小,在对水域、工业仓储用地、耕地等类别的分类正确率略低于支持向量机分类,但在住宅用地及林地的分类中优于支持向量机方法;支持向量机方法分类总体精度最高,但在交通运输用地分类中存在不足,对于住宅用地存在明显错分。
| % | |||
| 类别名称 | ELM | SVM | 最大似然法 |
| 林地 | 52.06 | 43.80 | 78.88 |
| 耕地 | 66.86 | 88.94 | 69.54 |
| 工业仓储用地 | 94.11 | 95.68 | 69.45 |
| 住宅用地 | 64.57 | 19.76 | 68.42 |
| 交通运输用地 | 64.55 | 57.37 | 80.69 |
| 水域 | 78.22 | 84.01 | 83.33 |
1) 极限学习机算法能有效地利用图像的信息进行地物分类,得到的分类结果与实际地物分类达到基本一致。
2) 极限学习机算法适用于遥感影像分类问题,其高效且稳定等特点明显优于SVM和最大似然法,符合当前追求效率的趋势。
3) 将极限学习机算法引入基于像元的监督分类中,该方法在遥感图像分类中有较好的推广性,但一些易混淆的地物根据像元值无法被正确分类。在之后的研究中,将优化极限学习机算法,结合地物本身特征对遥感影像进行分类,进一步提高分类精度,为影像分类提供理论和技术支持。
| [1] |
陈圣波, 刘彦丽, 杨倩, 等. 植被覆盖区卫星高光谱遥感岩性分类[J].
吉林大学学报(地球科学版), 2012, 42(6): 1959-1965.
Chen Shengbo, Liu Yanli, Yang Qian, et al. Lithologic Classification from Hyperspectral Data in Dense Vegetation Cover Area[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(6): 1959-1965. |
| [2] | Nitish S, Geoffrey H, Alex K, et al. Dropout:A Simple Way to Prevent Neural Networks from Overfitting[J]. Journal of Machine Learning Research, 2014, 15(6): 1929-1958. |
| [3] | Huang G B, Zhu Q Y, Siew C K. Extreme Learning Machine:A New Learning Scheme of Feedforward Neural Networks[J]. Proc Int Joint Conf Neural Netw, 2004, 2(2): 985-990. |
| [4] | Zong W W, Huang G B, Chen Y Q. Weighted Extreme Learning Machine for Imbalance Learning[J]. Neurocomputing, 2013, 101: 229-242. DOI:10.1016/j.neucom.2012.08.010 |
| [5] | Huang G B, Ding X J, Zhou H M. Optimization Me-thod Based Extreme Learning Machine for Classification[J]. Neurocomputing, 2010, 74: 155-163. DOI:10.1016/j.neucom.2010.02.019 |
| [6] | Zong W W, Huang G B. Face Recognition Based on Extreme Learning Machine[J]. Neurocomputing, 2011, 74(16): 2541-2551. DOI:10.1016/j.neucom.2010.12.041 |
| [7] | Huang G B, Li M B, Chen L, et al. Incremental Extreme Learning Machine with Fully Complex Hidden Nodes[J]. Neurocomputing, 2008, 71(4): 576-583. |
| [8] |
王士同, 钟富礼. 最小学习机[J].
江南大学学报(自然科学版), 2010, 9(5): 505-510.
Wang Shitong, Zhong Fuli. On Least Learning Machine[J]. Journal of Jiangnan University (Natural Science Edition), 2010, 9(5): 505-510. |
| [9] |
邓万宇, 郑庆华, 陈琳, 等. 神经网络极速学习方法研究[J].
计算机学报, 2010, 33(2): 280-287.
Deng Wanyu, Zheng Qinghua, Chen Lin, et al. Research on Extreme Learning of Neural Networks[J]. Chinese Journal of Computer, 2010, 33(2): 280-287. |
| [10] |
王杰, 毕浩洋. 一种基于粒子群优化的极限学习机[J].
郑州大学学报(理学版), 2013, 45(1): 100-104.
Wang Jie, Bi Haoyang. A New Extreme Learning Machine Optimized by PSO[J]. Journal of Zhengzhou University (Natural Science Edition), 2013, 45(1): 100-104. |
| [11] |
陈建原, 何建农. 基于在线连续极限学习机的图像分类改进算法[J].
福州大学学报(自然科学版), 2015, 42(2): 176-181.
Chen Jianyuan, He Jiannong. A Modified Algorithm for Image Classification Based on Online Sequential Extreme Learning Machine[J]. Journal of Fuzhou University (Natural Science Edition), 2015, 42(2): 176-181. DOI:10.7631/issn.1000-2243.2015.02.0176 |
| [12] |
王礼云, 毛文涛, 胡武鹏. 极限学习机多目标模型选择研究[J].
计算机仿真, 2014, 31(8): 387-391.
Wang Liyun, Mao Wentao, Hu Wupeng. Multi-Objective Model Selection for Extreme Learning Machine[J]. Computer Simulation, 2014, 31(8): 387-391. |
| [13] |
吴军, 王士同, 赵鑫. 正负模糊规则系统、极限学习机与图像分类[J].
中国图象图形学报, 2011, 16(8): 1408-1417.
Wu Jun, Wang Shitong, Zhao Xin. Positive and Negative Fuzzy Rule System, Extreme Learning Machine and Image Classification[J]. Journal of Image and Graphics, 2011, 16(8): 1408-1417. |
| [14] |
崔利凯, 孙建孟, 闫伟超, 等. 基于多分辨率图像融合的多尺度多组分数字岩心构建[J].
吉林大学学报(地球科学版), 2017, 47(6): 1904-1912.
Cui Likai, Sun Jianmeng, Yan Weichao, et al. Construction of Multi-Scale and Component Digital Cores Based on Fusion of Different Resolution Core Images[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(6): 1904-1912. |



