2. 吉林大学地球探测科学与技术学院, 长春 130026;
3. 河北省地矿局第一地质大队, 河北 邯郸 056001
2. College of GeoExploration Science and Technology, Jilin University, Changchun 130026, China;
3. No.1 Geological Brigade of Hebei Geology and Mineral Exploration Bureau, Handan 056001, Hebei, China
0 引言
地下管道是城市的生命线,是城市中最重要的基础设施,它担负着人们正常工作和生活的责任,具有传输能量、传递信息,水源供应和排放废液等一系列重要的职能。但绝大多数城市地下管道分布并不是很清楚,相关部门对于管道分布图的资料管理也不够规范,甚至一些废旧居民区和废旧工业区没有管道图。这些问题都给城市扩张及建设造成了不小的困难,有时给人们的生产和生活造成困难(如停水停电等)或导致事故,甚至人员伤亡。管道探测不仅对城市建设、改造等起到了极为重要的作用,甚至对于整个城市的发展进步都至关重要。因此对地下管道快速准确地识别,是我们目前很有必要做的工作[1]。
探地雷达(GPR)是一种无损探测技术,通过天线向地下发射高频电磁波,接收到的电磁波由于地下媒介电磁特性和物理性质的差别,其路径、强度、波形都会发生改变,以此探知地下物质的物性差别[2]。
20世纪90年代出现了研究探地雷达的热潮,这是我国探地雷达对地下管道探测技术发展的起步阶段。在此之后,我国科研人员在探地雷达方面投入了大量的人力物力,我国的探测技术趋于成熟。在90年代中后叶,国防科技大学研究出一种对道路分辨率为4 mm左右、使系统分辨率达到3~5 cm的探地雷达[3]。此后,探地雷达在工程方面的应用日渐增多,对管道探测的研究亦日趋成熟[4]。然而常规探地雷达大多数是单极化雷达,单极化雷达是采用固定极化方式的天线来发射和接收电磁波信号,只接收共极化信息[5],故得到的是单极化数据。但单极化数据信息量远不足以满足实际需求,对管道目标准确快速的识别造成了困难,于是全极化探地雷达在单极化雷达之后得到了快速的发展[6-12]。
全极化探地雷达是通过接收来自不同极化方向的电磁波,利用不同目标体反射回来的电磁波信号中矢量特性的不同以及各矢量分量之间的关系,更好地获得目标体的位置及走向等各方面信息[12]。其优点是能够分析目标体的极化特性,由全极化散射矩阵表述。通过该矩阵可以了解目标体在每个测点上的极化特征,这些极化特征既包括共极化信息也包括交叉极化信息,从而能够获取目标体较为全面的极化信息。极化分解技术主要就是通过分析目标体的全极化信息,提取目标体的极化属性,有效地识别目标体[7]。
1982年,Huynen[13]首次阐明了目标分解理论。自这一独创性的工作开展以来,研究学者相继提出了众多极化分解方法,主要可分为4类[14]:基于Kennaugh矩阵的二分量分解方法;基于特征矢量的目标极化分解;基于散射模型的目标极化分解;基于相干分解的极化目标分解理论。本文所用的H/α极化分解方法是Cloude和Pottier在1997年提出的。该方法基于Kennaugh矩阵,利用二阶统计量平滑算法提取平均参数[15]。
本文将全极化探地雷达与H/α分解方法结合,提取地下目标的极化属性,识别地下管道。由于探地雷达具有数据采集速度快、数据处理快捷方便等优点,因此这种结合方法在快速识别管道问题上有一定的优势。但实际地下管道并不是单独存在的,其或者与其他管道彼此相互影响,或者受其他极化属性目标体的影响,难以识别。为了克服复杂环境下管道难以识别的问题,我们设置了2个不同的实验环境:多个管道彼此之间相互影响的实验环境和将管道和球(其他极化属性的目标体)放置在一起的实验环境,用全极化探地雷达识别。
1 全极化探地雷达地下管道探测原理 1.1 全极化探地雷达系统全极化步进频率探地雷达系统(图 1)由矢量网络分析仪、三维直角坐标机器人、PC控制单元和全极化天线构成。将发射天线、接收天线分别接在发射端口和接收端口,即可构成完整的全极化探地雷达系统。该系统具有精确定位、测量、自动化存储数据等功能,可获得高质量的全极化数据。
在本文中用到的矢量网络分析仪的型号是E5071C,频带宽度为:9 kHz~8.5 GHz,扫描点数可达1 601,输出功率为-15~10 dBm,最大输入功率为20 dBm。通过网络分析仪,可以发射信号和接收信号,能够进行简单的数据处理。在使用网络分析仪之前首先要进行校准,校准主要是去除电缆及仪器本身的干扰。我们一般用双端口校准,校准件的型号是E5052C,包含4个校准件,分别是短路校准件、开路校准件、负载校准件和直通校准件。
三维直角坐标机器人用于空间位置精确定位,能在x, y, z 3个方向上移动,测量精度可达0.1 mm。通过PC控制单元控制三维直角坐标机器人的移动。
在该全极化探地雷达系统中,所用天线是Vivaldi天线。天线在探地雷达系统中至关重要,极化天线分为水平极化(H极化)天线和垂直极化(V极化)天线两种。电磁波的传播方向与极化方向一致时,我们称之为H极化;波的传播方向与极化方向垂直称为V极化,由H极化和V极化可以构成交叉极化(VH极化或者HV极化)[7]。
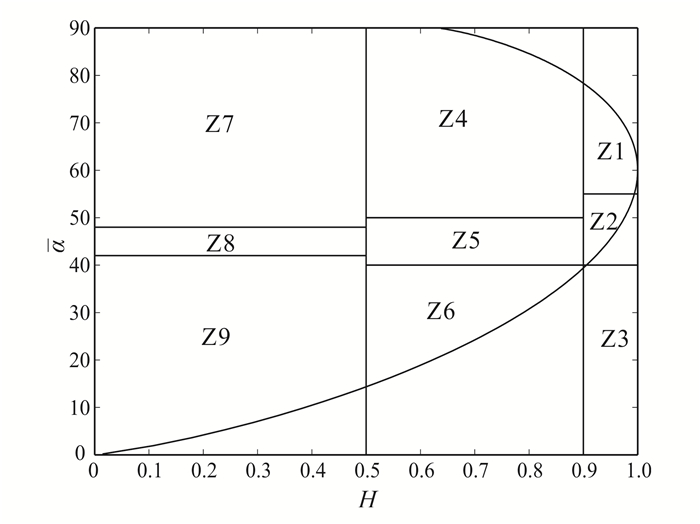
1.2 H/α极化分解H/α(H为极化熵,主要衡量散射数据内在的可逆性;α为极化散射参数,可以识别主要的散射机制)分解是一种非监督分类方法,它能够表征所有的随机散射机制,不依赖特定的统计分布假设,也不受多变量模型物理约束条件的限制。利用对3 × 3相干矩阵的特征矢量分析,将相干矩阵分解成不同的特征矢量及对应的特征值。为了识别出目标体主要存在的散射机制,首先将H值和α值构成一个二维平面,并将该二维特征平面分成9个基本区,每个区域对应不同的散射机制,在H和α可能的组合范围内,各区的边界位置由散射机制具有的整体特性来确定,且边界设定存在一定的任意性,并且与某个数据集无关。该方法的实质是将物理散射过程作出几何划分,这是使散射特征分类问题成为非监督分类且与实际散射特征无关的关键[15-17]。
假设在散射和散射体全部确定的情况下,完全散射就能够由散射矩阵描述。在单站后向散射情况下,发射天线和接收天线在同一位置时,测线中每个测点的散射矩阵S可表示为
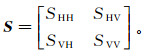 (1)
(1) 式中, SHH,SHV,SVH和SVV是散射系数。SHH和SVV代表入射场和散射场的极化方式相同,称之为“同极化”项;SVH和SHV代表入射场和散射场极化方式相互正交,称之为“交叉极化”项。由于发射天线和接收天线是可交换的,且传播的介质也满足互易性,因此后向散射矩阵也满足互易性,即有SHV=SVH[14]。那么目标矢量Ω可写成
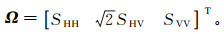 (2)
(2) 那么协方差矩阵C就可以写成
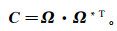 (3)
(3) 式中:*代表共轭变换;上角标T表示转置。
将目标矢量Ω代入式(3)可得
 (4)
(4) 计算协方差矩阵C的特征值和特征向量,可将公式(4)化为标准化形式[17-19]:
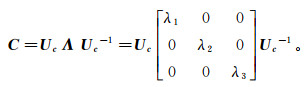 (5)
(5) 其中,
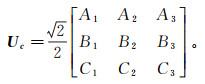 (6)
(6) 式中:
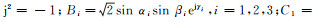
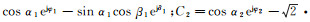

 (7)
(7) 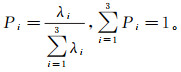 (8)
(8) 式中,Pi是特征值λi获得的伪概率。因特征值旋转不变,极化熵也旋转不变。参数αi与随机过程相关,最好取其平均值α,且α是旋转不变的[29]。
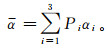 (9)
(9) 至此,我们得到了参数H和α,画出2维H/α分类空间(图 2)。该分类空间描述了对于随机散射问题的H/α分类平面。
| 区域 | 散射机制 |
| Z9 | 低熵表面散射。在这个区域出现低熵散射 |
| Z8 | 低熵偶极散射。在这个区域出现强烈相关机制 |
| Z7 | 低熵二次散射。如孤立的电介质和金属二面角反射器 |
| Z6 | 中等熵表面散射。此区域反映了表面粗糙度的变化 |
| Z5 | 中熵植被散射。此区域对应中等熵但是偶极散射机占主导 |
| Z4 | 中等熵大量散射。此区域对应中度熵的二面角散射 |
| Z3 | 高熵表面散射。对于散射机制的识别这个区域被认为是不可实现的 |
| Z2 | 高熵植被散射,对应随机的各向异性散射体 |
| Z1 | 高熵大量散射,对应复杂的构造 |
我们在实验室均匀的沙槽中分别对单一管道、多个管道彼此之间相互影响以及管道受其他属性目标体影响3种不同类型的实验进行全极化测量。
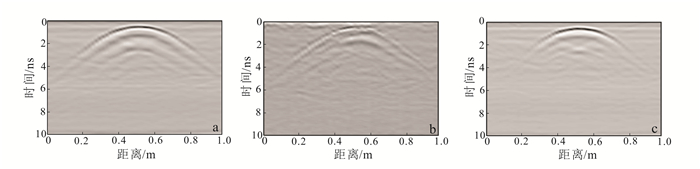
2.1 单一管道极化属性分析将直径为5 cm的金属圆柱体(图 3)埋在2.5 m×2.5 m均匀的白沙沙槽中,目标体大致埋在沙槽中间位置,埋深15 cm左右。用金属圆柱体模拟实际环境中的管道,测线布设在目标体正上方,用全极化探地雷达系统进行测量,分别得到了HH,HV,VV 3种极化方式的测量剖面(图 4)。

|
| 图 3 两个实验目标体 Figure 3 Two experimental objects |
|
|
|
| a.HH,水平发射水平接收;b.HV,水平发射垂直接收;c.VV,垂直发射垂直接收。 图 4 单一管道目标体剖面图 Figure 4 Profiles of a single pipeline |
|
|
在每个测点上可获得地下目标体的全极化散射矩阵,对选定区域内的每个测点上的全极化散射矩阵进行H/α极化属性分解,可得到图 5。从图 5看出,数据点主要集中在Z8区。Z8区主要存在的是低熵偶极子散射和强相关散射机制。因此我们知道地下目标体的散射特性与Z8区类似,发生低熵偶极子散射。根据这个特性,可以将地下目标体识别为管道等线性目标体。这验证了全极化探地雷达数据能够快速有效地识别地下管道,说明了H/α分解在地下管道识别中可发挥极为重要的作用。

|
| 图 5 单一管道目标的H/α的分布图 Figure 5 Distribution of H/α of a single pipeline |
|
|
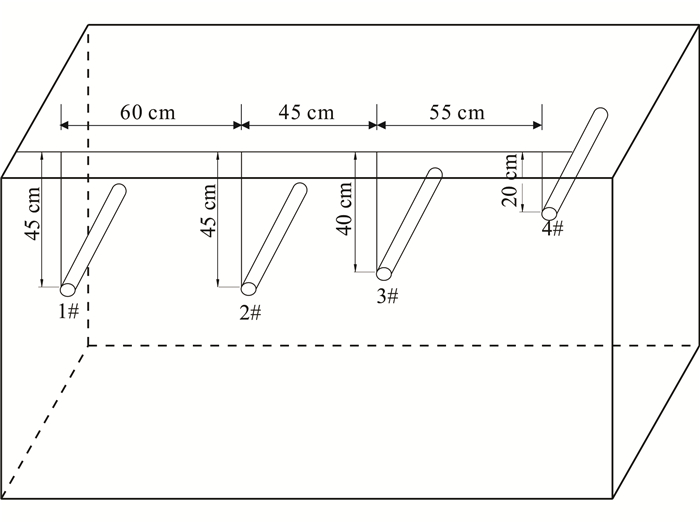
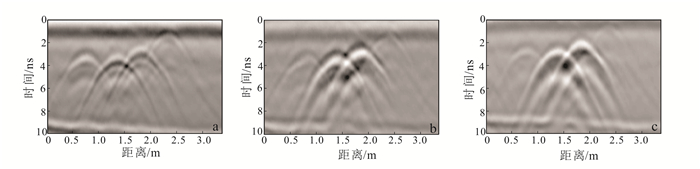
沙槽中均匀沙的相对介电常数约为4,沙中埋置4个相距很近的管道,其分布如图 6所示,从左到右管道的埋深依次为45, 45, 40, 20 cm,横向间隔为60,45,55 cm。中间两个管道(2#、3#)是金属管,两侧分别为PVC管,测量间隔为2 cm。用全极化探地雷达系统进行全极化测量,分别得到了HH,HV,VV 3种极化方式的测量剖面(图 7)。
|
| 图 6 管道的三维立体图 Figure 6 Three dimensional view of four pipes |
|
|
|
| a.HH,水平发射水平接收;b.HV,水平发射垂直接收;c.VV,垂直发射垂直接收。 图 7 4根管道的剖面图 Figure 7 Profiles of the four pipelines |
|
|
由于4根管道的极化属性相互影响,我们对4根管道从左到右依次进行极化属性的分析。对每个管道选定区域内的测点上的全极化散射矩阵进行H/α极化分解,得到图 8。从图 8看出,数据点依然主要集中在Z8区。由于管道的极化属性相同,即使极化属性相互影响,也依然是同属性的影响,不会偏离管道所在的Z8区。因此我们在众多线性管道中也可以识别地下任何一个管道。这就验证了全极化探地雷达数据能够快速有效地识别地下管道,说明了H-α分解在地下管道识别中发挥着极为重要的作用。

|
| a.第一根管道;b.第二根管道;c.第三根管道;d.第四根管道。 图 8 4根金属管道的H/α的分布图 Figure 8 Distribution of H/α of the four metal pipelines |
|
|
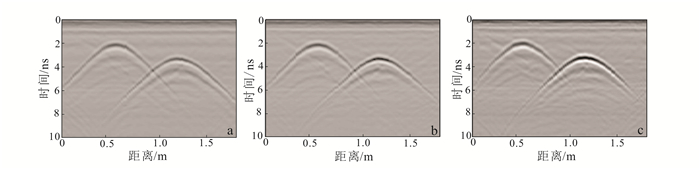
将直径为5 cm的金属圆柱体和直径为15 cm的实心金属球(图 3)埋在各向同性的白沙中,2个目标体大致在沙槽中间位置,目标体相距60 cm左右。用全极化探地雷达系统进行测量,测线依然布设在目标体正上方,分别得到了HH,HV,VV 3种极化方式的测量剖面(图 9)。
|
| a.HH,水平发射水平接收;b.HV,水平发射垂直接收;c.VV,垂直发射垂直接收。 图 9 管道和金属球在全极化GPR系统测量下得到的剖面图 Figure 9 Profiles of pipeline and ball with full polarimetric GPR system |
|
|
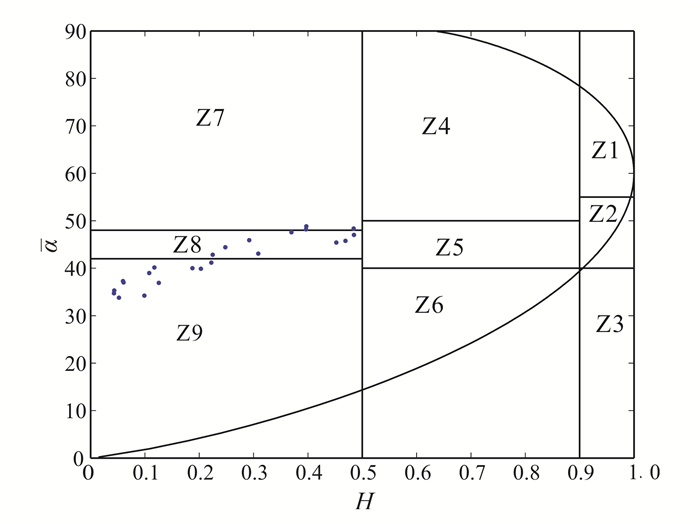
在管道受非线性目标体极化属性影响的情况下,首先对管道进行极化属性识别。对选定区域内的每个测点上的全极化散射矩阵进行H/α极化分解,得到图 10。从图 10看出,数据点依然主要集中在Z8区,但是由于受到非线性目标体球的影响,向球所在的Z9区有一定的偏移。因此我们得出在管道受其他非线性目标体极化属性影响的情况下,依然能识别地下管道,但由于受到非线性目标体极化属性的影响会向该目标体所在的区有一定的偏移。
|
| 图 10 管道在非线性目标体球影响下的H/α的分布图 Figure 10 Distribution of H/α of the pipe under the influence of nonlinear target ball |
|
|
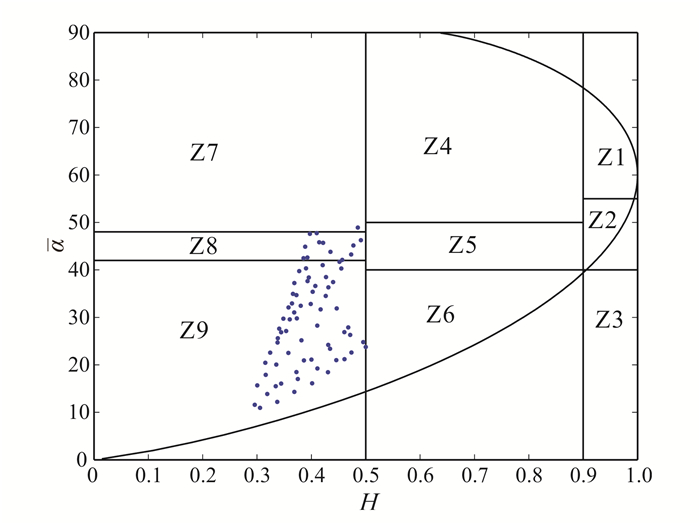
为了验证目标体之间由于极化属性相互影响致使数据点有一定的偏移想法的正确性,对此非线性目标体金属球进行了极化属性的分析,得到图 11。从图 11看出,球的数据点集中在Z9低熵表面散射区。但认真观察会发现,由于线性管道极化属性的影响,位于Z9区的数据点却向Z8线性目标体区有一定的偏移,但主要的数据点依然集中在Z9区。
|
| 图 11 金属球在管道的影响下的H/α的分布图 Figure 11 Distribution of H/α of the ball under the influence of pipeline |
|
|
综上,本文验证了目标体之间由于极化属性的相互影响而有一定偏移想法的正确性;其次验证了即使由于其他非线性目标体极化属性的影响,依然可以识别出地下管道,但管道会受其他非线性目标体的影响,有一定的偏移;最后验证了全极化探地雷达数据能够快速有效地识别地下管道,说明了H/α分解在地下管道识别中可发挥极为重要的作用。
3 结论与展望1) 采用全极化探地雷达方法获取地下管道的全极化数据,结合H/α分解技术提取了地下管道的极化属性H和α,并将其投影在H/α构成的二维特征分类空间的平面中,根据数据点主要存在的区,可识别出目标体存在的主要散射机制,从而可识别地下管道。
2) 对单个管道进行H/α分解,全极化探地雷达系统能够快速有效地识别地下管道;对4个相距很近的管道进行H/α分解,在多个线性管道极化属性相互影响的情况下也可以识别出任何一个管道;在管道受其他非线性目标体极化属性影响的情况下,对管道进行H/α分解,依然可以识别出地下管道,但由于受到非线性目标体极化属性的影响会向该目标体所在的区有一定的偏移。证明了H/α极化属性分析方法可应用于地下管道探测的全极化数据,能够快速、准确地识别地下管道。
3) 对非管道目标在H/α平面中投影的数据点若和管道投影的数据点位于同一区,则不能识别出地下管道,需要进步一完善该方法。本文只讨论了全极化雷达和H/α分解技术在地下管道识别方面的应用,可进一步扩展到对地下任一目标体的识别,例如可扩展到军事中,对于地下未爆炸物和地雷的识别。
| [1] |
张鹏, 董韬, 马彬, 等. 基于探地雷达的地下管线管径探测与判识方法[J].
地下空间与工程学报, 2015, 11(4): 1023-1032.
Zhang Peng, Dong Tao, Ma Bin, et al. Research on Interpreting the Information of Underground Pipeline's Diameter Detected by GPR[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(4): 1023-1032. |
| [2] |
陈义群, 肖柏勋. 论探地雷达现状与发展[J].
工程地球物理学报, 2004, 2(2): 149-155.
Chen Yiqun, Xiao Boxun. On the Status Quo and Development of Ground Penetrating Radar[J]. Chinese Journal of Engineering Geophysics, 2004, 2(2): 149-155. |
| [3] |
张文军. 基于雷达的地下管道探测关键技术研究[D]. 长春: 长春理工大学, 2016.
Zhang Wenjun. Research on Key Technology of Underground Pipeline Detection Based on Radar[D]. Changchun: Changchun University of Science and Technology, 2016. |
| [4] |
张文波, 魏文博, 景建恩, 等. 利用探地雷达的极化特性检测建筑物结构[J].
吉林大学学报(地球科学版), 2008, 38(1): 156-160.
Zhang Wenbo, Wei Wenbo, Jing Jian'en, et al. Application of Ground Penetrating Radar Polarization in the Concrete Structure Detection[J]. Journal of Jilin University(Earth Science Edition), 2008, 38(1): 156-160. |
| [5] |
汪梦奇. 分时极化雷达系统及其实现技术研究[D]. 北京: 北京理工大学, 2015.
Wang Mengqi. The Studies on Time-Division Polarimetric Radar System and Its Implementation Technology[D]. Beijing: Beijing Institute of Technology, 2015. |
| [6] |
李丽丽, 冯晅, 鹿琪, 等. 极化步频探地雷达系统初步研究[J].
吉林大学学报(地球科学版), 2008, 38(1): 150-152.
Li Lili, Feng Xuan, Lu Qi, et al. Preliminary Study on Polarization Step Frequency Radar Systems[J]. Journal of Jilin University(Earth Science Edition), 2008, 38(1): 150-152. |
| [7] |
于月. 全极化探地雷达H/α特征分解技术研究[D]. 长春: 吉林大学, 2016.
Yu Yue. Development of H-Alpha Feature Decomposition Technology For Full-Polarimetric Ground Penetrating Radar[D]. Changchun: Jilin University, 2016. |
| [8] |
梁文婧. 全极化步进频率探地雷达硬件系统研究[D]. 长春: 吉林大学, 2012.
Liang Wenjing. Full-Polarimetric Step-Frequency GPR System Research[D]. Changchun: Jilin University, 2012. |
| [9] |
李丽丽. 全极化探地雷达采集系统及校准技术初探[D]. 长春: 吉林大学, 2010.
Li Lili. Fully-Polarimetric GPR Acquisition System and Calibration Technique Preliminary Study[D]. Changchun: Jilin University, 2010. |
| [10] | Xuan F, Yue Y, Cai L, et al. Subsurface Polarimetric Migration Imaging for Full Polarimetric Ground-Penetrating Radar[J]. Geophysical Journal International, 2015, 202(2): 1324-1338. DOI:10.1093/gji/ggv208 |
| [11] |
邹立龙. 全极化探地雷达正演模拟及极化校准技术[D]. 长春: 吉林大学, 2012.
Zou Lilong. Forward Modeling and Calibration Technique of Full-Polarimetric GPR[D]. Changchun: Jilin University, 2012. |
| [12] |
尤志鑫. 探地雷达地下浅层砂体和管道探测技术研究[D]. 长春: 吉林大学, 2016.
You Zhixin. Study of Underground Shallow Sandstone and Pipeline with Ground Penetrating Radar[D]. Changchun: Jilin University, 2016. |
| [13] | Huynen J R. A Revisitation of the Phenomenological Approach with Applications to Radar Target Decomposition[R]. University of Illinois at Chicago: Department of Electrical Engineering and Computer Sciencesrr, 1982. |
| [14] |
LeeJ S, PottierE.
极化雷达成像基础与应用[M]. 北京: 电子工业出版社, 2013.
Lee J S, Pottier E. Fundamentals and Applications of Polarimetric Radar Imaging[M]. Beijing: Publishing House of Electronics Industry, 2013. |
| [15] | Cloude S R, Pottier E. An Entropy Based Classifi-cation Scheme for Land Applications of Polarimetric SAR[J]. IEEE Trans Geosci Remote Sens, 1997, 35(1): 68-78. DOI:10.1109/36.551935 |
| [16] | Zhao J G, Sato M. Radar Polarimetry Analysis Applied to Single-Hole Fully Polarimetric Borehole Radar[J]. IEEE Trans Geosci Remote Sens, 2006, 44(12): 3547-3554. DOI:10.1109/TGRS.2006.882260 |
| [17] | Yilmaz Ö, Doherty S M. Seismic Data Analysis:Processing, Inversion, and Interpretation of Seismic Data[M]. 2nd ed. Tulsa: Soc Exploration Geophys, 2001. |
| [18] | Lauren F F, Pottier E, Lee J S. Unsupervised Classification of Multifrequency and Fully Polarimetric SAR Images Based on the H/A/Alpha-Wishart Classifier[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2332-2342. DOI:10.1109/36.964969 |
| [19] | Lee J S, Grunes M R, Ainsworth T L, et al. Unsupervised Classification of Polarimetric SAR Images by Applying Target Decomposition and Complex Wishart Distribution[J]. IEEE Trans Geosci Remote Sensing, 1999, 37: 2249-2258. DOI:10.1109/36.789621 |
| [20] | Lee J S, Schuler D L, Ainsworth T L. Polarimetric SAR Data Compensation for Terrain Azimuth Slope Variation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2153-2163. DOI:10.1109/36.868874 |
| [21] | Lee J S, Schuler D L, Ainsworth T L, et al. On the Estimation of Radar Polarization Orientation Shifts Induced by Terrain Slopes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(1): 30-41. DOI:10.1109/36.981347 |
| [22] | Pottier E. Unsupervised Classification Scheme and Topography Derivation of POLSAR Data on the H/A/α Polarimetric Decomposition[C]//Theorem Proceedings of the 4th International Workshop on Radar Polarimetry. Nantes: Taylor & Francis Online, 1998: 535-548. |
| [23] | Pottier E, Boerner W M, Schuler D L. Estimation of Terrain Surface Azimuthal/Range Slopes Using Polarimetric Decomposition of POLSAR Data[C]//Proceedings of IGARSS 1999. Hambourg: IEEE, 1999. |
| [24] | Schuler D L, Lee J S, Grandi G D. Measurement of Topography Using Polarimetric SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(5): 1266-1277. DOI:10.1109/36.536542 |
| [25] | Schuler D L, Lee J S, Ainsworth T L, et al. Terrain Slope Measurement Accuracy Using Polarimetric SAR data[C]//Proceedings of IGARSS 1999. Hambourg: IEEE, 1999. |
| [26] | Schuler D L, Lee J S, Ainsworth T L, et al. Pola-rimetric DEM Generation from POLSAR Image Information[C]//Proceedings of URSI-XXVIth General Assembly. Toronto: University of Toronto, 1999. |
| [27] | Schuler D L, Lee J S, Ainsworth T L, et al. Terrain Topography Measurement Using Multipass Polarimetric Synthetic Aperture Radar Data[J]. Radio Science, 2000, 35(3): 813-832. DOI:10.1029/1999RS002266 |
| [28] | Fisher E, McMechan G A, Annan A P, et al. Exa-mples of Reverse-Time Migration of Single-Channel, Ground-Penetrating Radar Profiles[J]. Geophysics, 1992, 57(4): 577-586. DOI:10.1190/1.1443271 |
| [29] | Lee J S, Pottier E. Polarimetric Radar Imaging:From Basics to Applications[M]. Boca Raton: University of Rochester, 2009. |
| [30] | Cassidy N J. Evaluating LNAPL Contamination Using GPR Signal Attenuation Analysis and Dielectric Property Measurements:Practical Implications for Hydrological Studies[J]. J. Contaminant Hydrol, 2007, 94(1/2): 49-75. |