2. 上海交通大学船舶海洋与建筑工程学院, 上海 200240;
3. 国网新源控股有限公司技术中心, 北京 100161;
4. 厦门市建设局, 福建 厦门 361003
2. School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China;
3. Technology Center, State Grid Xinyuan Company Ltd, Beijing 100161;
4. Xiamen Construction Bureau, Xiamen 361003, Fujian, China
0 引言
综合管廊是建于城市地下用于容纳两类及以上城市工程管线的构筑物及附属设施[1]。地下综合管廊相比直埋管线具有很多优点,是城市现代化发展的必然趋势,目前很多城市正在开展综合管廊的建设或规划。既有的震害记录表明,地下结构在地震过程中会遭到严重破坏,应引起地震工作者的重视[2]。由于室内试验费用高、周期长,数值分析成为地下结构动力响应分析的重要手段。对于半无限地基中地下结构的动力响应分析,目前广泛采用的数值模拟技术是从半无限域中切取有限尺寸的近场计算区,此时需要在计算域边界上引入虚拟的人工边界,以消除反射、模拟远场介质的辐射阻尼效应[3-7]。合理设置人工边界是实现对真实波动的直接模拟、解决土-结构相互作用问题的关键。人工边界可以分为静力人工边界和动力人工边界两大类。静力人工边界是基于静力学基本理论建立的,但已有研究表明,以固定边界为代表的静力人工边界与波动在半无限介质中的传播规律不符[8-9]。目前广泛应用的动力人工边界主要是基于单侧波动概念的局部人工边界,比如黏性边界[10-11]、黏弹性边界[12-17]、透射边界[18]等。
因概念清楚、简单方便,黏性边界应用最为广泛,但其仅考虑了对散射波能量的吸收。从物理概念上理解,施加黏性边界后的力学模型为悬浮在空中的脱离体,其在低频力作用下可能发生整体漂移;此外,黏性边界是基于一维波动理论提出的,简单地将其推广到多维情况将导致相当误差[19]。相比而言,黏弹性边界可以约束动力问题中的零频分量,能够模拟人工边界外半无限介质的弹性恢复性能,具有良好的稳定性和较高的精度。不过,黏弹性边界建模时,需逐点计算并施加弹簧及阻尼器,前处理工作量大;实际应用中,为了便于施加黏弹性边界,通常采用一些近似处理,这会对计算精度造成一定程度的影响[20]。无论是黏性边界还是黏弹性边界都属于吸收边界,只考虑了对外行波的吸收效果,未考虑地震动输入问题。地震动输入一般基于波场分离法,即在底边界输入入射波场、在侧边界输入自由波场来实现,因此在均匀岩土体中,侧边界的自由波场采用一种延时的方法得到。但是在实际的数值计算中,施加侧边吸收边界和输入自由场地震动工作量浩大,前处理繁杂;而且在实际岩土工程中,岩土体往往具有不均匀性和非线性的力学特征,通常会出现水平分层现象,每一层土体具有不同的动力学特性。此时很难通过简单的延时方法得到自由场地的地震反应,而要利用波的频域分析、反射透射理论、波幅系数转换等更复杂的波动理论来计算波动在土层间的传播与叠加。
要想解决此问题,可以采用SHAKE91和EERA等一维土层动力反应分析软件计算水平成层场地的地震反应或者在有限元(有限差分)软件中同步计算自由场地地震反应,从而获得侧边界地震动输入所需要的自由波场,这样也就实现了自由场运动和计算模型侧边界的完美耦联。此理论也就是我们所熟悉的自由场边界的思想基础,它最早由Seed等[21]提出,目前已在PLAXIS、FLAC等数值模拟软件中得到广泛应用,但这些人工边界本身固有的优缺点及其局限性仍然存在。以PLAXIS中内置的黏性边界为例,其松弛系数C1和C2需要建立一系列模型进行试算确定,才可获得较好的动力响应效果;自由场边界具有较好的场地动力响应,但其适用性也需进行验证和深入探讨。
为研究综合管廊动力边界条件对地震动力响应的影响,本文以厦门地区的代表性土层为例,分别研究了固定边界、黏性边界和自由场3种人工边界在Rayleigh波和地震底部剪切波作用下的场地响应,并根据加速度时程和拟绝对加速度反应谱(PSA)评价了3种边界的有效性;进而提出综合管廊地震动力分析的优化动力边界组合。
1 边界条件在数值分析软件中的实现 1.1 黏性边界黏性边界的基本思想是在人工边界上设置阻尼器,以吸收振动过程中的散射波能量。PLAXIS软件提供了基于该方法建立的黏性边界条件。地震分析中,如果在模型底部设置黏性边界,则地震输入应为荷载时程。
以边界上x方向的某一阻尼器为例,其吸收的法向和切向应力分量分别为
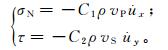 (1)
(1) 式中:σN为沿黏性边界作用的法向应力;τ为沿黏性边界作用的切向应力;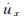
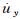
松弛系数C1和C2用于改善黏性边界的波动吸收效果:C1调整沿边界法向的能量耗散;C2调整沿边界切向的能量耗散。若边界上只受到法向波动,则无需考虑松弛,此时C1=C2=1。一般情况下,波动方向并非仅垂直于边界,而是沿任意方向,此时应调整C2的值以改善吸收效果。
1.2 自由场边界黏性边界与黏弹性边界对爆破等内源问题比较有效,但因其均属于吸收边界,主要考虑对外行波的吸收效果,而没有考虑地震动的输入问题,因此尚不能很好地解决地震等外源问题。通常,地震波考虑为底边界垂直入射,此时两侧边界内行波场为自由波场[22]。自由场边界通过“强制”自由场运动,同时保证工程计算区域产生的外行波被适当地吸收,以模拟无限域边界条件。在有限元软件中,通过在模型四周生成与其边界节点对应的自由场网格来实现自由场边界条件,主网格的侧边界与自由场网格通过阻尼器(黏性边界)进行耦合,以吸收有结构存在时入射地震波发生的散射;在求解过程中,主网格进行计算时自由场网格也进行同步运算,自由场网格的不平衡力会施加到主网格的侧边界上以满足侧边界上的位移和应力条件。自由场提供的条件与无限场地完全相同。自由场边接触面上所施加的沿x、y、z方向的不平衡力Fx、Fy、Fz表达式为
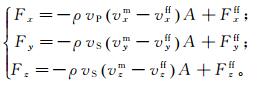 (2)
(2) 式中:A为自由场节点影响面积;vxm、vym、vzm为主网格边界节点沿x、y、z方向的速度;vxff、vyff、vzff为自由场节点沿x、y、z方向的速度;Fxff、Fyff、Fzff为自由场单元沿x、y、z方向正应力产生的节点力。
PLAXIS中自由场边界的实现与上述方法类似。自由场边界由荷载时程和黏性边界组成,荷载时程由自由场运动产生。荷载时程和黏性边界结合而成的自由场边界,能够同时实现模型边界上地震动输入和对散射波的吸收。
2 动力有限元数值模型 2.1 工程概况厦门湖边水库综合管廊长约5.2 km,断面形式主要有矩形单仓(3.0 m×2.8 m)、双仓(5.6 m×2.8 m)(图 1)和三仓(8.6 m×2.8 m),以及单仓圆形(内径3.4 m),管廊埋深3.0~5.0 m,管廊结构为预制形式;纳入的管线主要为110、220 kV高压电缆,10 kV电力、通讯电缆,给水、有线电视、交通信号及预留管线。

|
| 图 1 双仓综合管廊 Figure 1 Double chamber utility tunnel |
|
|
基坑开挖揭露土层情况:填土(已建道路为填筑土),最大厚度2.4 m;以下为粉质黏土、残积土、全风化花岗岩、强风化花岗岩及中风化花岗岩。填土透水性中等,总体水量不大;粉质黏土、残积土及散体状强风化花岗岩属弱透水弱含水层,水量较小。场地局部为空地,周边房屋大部分为3~4层的砖混结构民房及厂房,场地内及附近无不良地质作用和地质灾害。综合管廊采用明挖基坑埋设预制管廊结构,基坑宽度为9~12 m,开挖深度一般为5.5 m,局部地段基坑开挖深度最大为14.5 m。图 2为单仓圆形现场吊装图。

|
| 图 2 预制综合管廊现场吊装 Figure 2 Field hoisting of prefabricated utility tunnel |
|
|
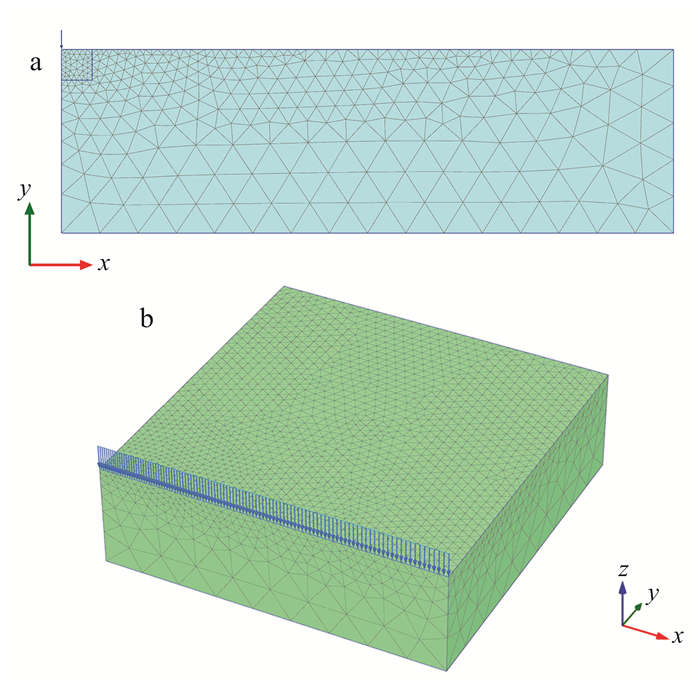
为了对比二维模型与三维模型对计算结果的差异,分别建立二维数值模型和三维数值模型。二维数值模型水平方向长100 m,地表以下土体深度取30 m,如图 3a所示。三维模型尺寸为100 m×100 m×30 m,如图 3b所示。静力边界均为模型侧边界法向约束,底部固定约束。
|
| a.二维;b.三维。 图 3 动力边界研究数值模型 Figure 3 Numerical models for studying dynamic boundary conditions |
|
|
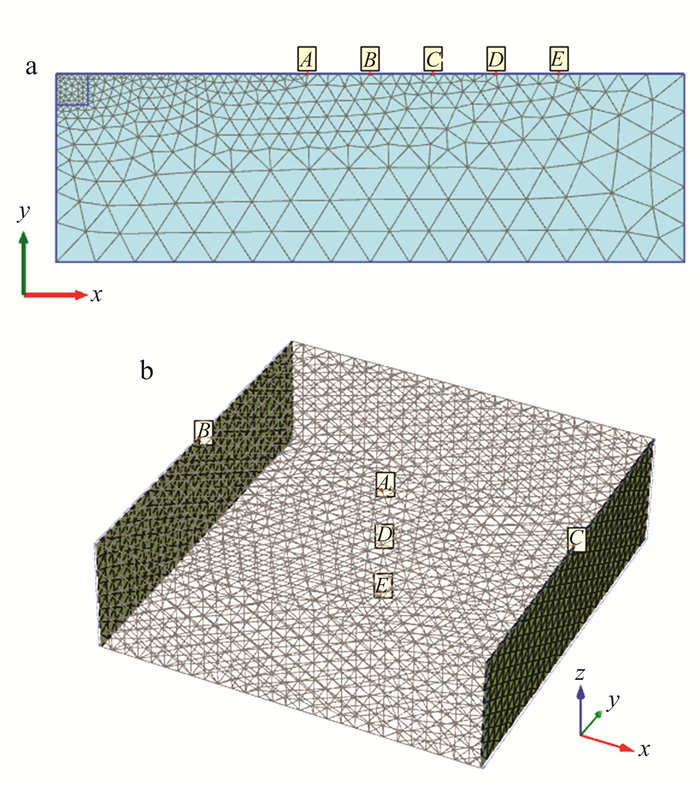
计算过程中,在模型中设置监测点(图 4)。图 4a中,A,B,C,D,E的坐标分别为(40, 0),(50, 0),(60, 0),(70, 0),(80, 0);图 4b中,A,B,C,D,E的坐标分别为(50, 50, 0),(0, 50, 0),(100, 50, 0),(50, 50, -15),(50, 50, -30)。
|
| a.二维;b.三维。 图 4 不同模型监测点布置 Figure 4 Layout of monitoring sites in different numerical models |
|
|
厦门地铁深基坑开挖深度15.0~25.0 m揭示的土层主要为人工填土、粉质黏土、淤泥质土和残积砂质黏性土。表层人工填土厚度一般为0.5~3.0 m;粉质黏土和淤泥质土在大部分地区普遍连续分布,埋深较浅;残积土埋深和厚度变化大,埋深为8.0~20.0 m,平均厚度可达10.0~16.0 m。城市综合管廊通常埋深较浅,一般情况下会处于粉质黏土层中,因此,主要取粉质黏土层作为综合管廊的埋置地层。
土体本构模型采用小应变硬化模型(hardening soil model with smallstrain stiffness,HSS)。以厦门地区为例,结合地勘报告及参数优化结果,确定地基土基本物理力学参数见表 1。
| 参数 | 人工填土 | 粉质黏土 |
| γ/(kN/m3) | 18 | 18.4 |
| E50ref/MPa | 6 | 5 |
| Eoedref/MPa | 6 | 5 |
| Eurref/MPa | 30 | 25 |
| c′ref/kPa | 25 | 37 |
| φ′/(°) | 15 | 15 |
| G0ref/MPa | 30 | 30 |
| γ0.7/10-3 | 0.30 | 0.15 |
| α/10-3 | 0.25 | 0.65 |
| β/10-3 | 0.25 | 0.65 |
| Rinter | 0.5 | 0.5 |
| K/(m/d) | 0.500 | 0.003 |
| 注:γ.重度;E50ref.三轴固结排水剪切实验的参考割线模量;Eoedref.固结实验的参考切线模量;Eurref.三轴固结排水卸载-再加载试验的参考卸载再加载模量;c′ref.有效黏聚力;φ′.有效内摩擦角;G0ref.小应变刚度试验的参考初始剪切模量;γ0.7.割线剪切模量衰减为0.7倍的初始剪切模量G0时对应的剪应变;α,β.阻尼系数;Rinter.界面折减系数;K.渗透系数。 | ||
福建省南部是东南沿海地震带活动相对频繁和强烈的地区,自1445年以来共发震级Ms≥5的强震8次。厦门市地处我国东南沿海地震带,遭受的震害主要是区外强震的波及。根据剪切波速测试结果,依国标《铁路工程抗震设计规范》(GB50111-2006)[23]有关标准划分,场地土类型为软弱土。另据钻探揭露和波速测试结果,场地覆盖层厚度小于50 m,依《建筑抗震设计规范》(GB50011-2001)[24]有关标准划分,拟建场地类别综合按Ⅱ类考虑。
为了模拟动力荷载产生的Rayleigh波,借鉴Lamb[25]问题施加荷载的方式,在边界上施加一个脉冲激励荷载。动力荷载采用随时间按三角形变化的荷载来模拟,自0.05 s之后开始施加荷载,荷载持续时间取0.025 s,荷载振幅取50 kN。关于该方法激励Rayleigh波的可行性笔者已在文献[26]中论证。
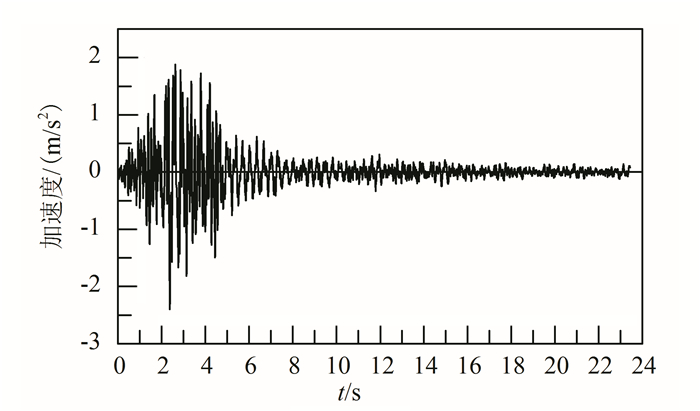
由于本文的重点在于研究边界条件对地震动力响应的影响,而非实际综合管廊的动力响应分析,因此采用PLAXIS程序的美国Upland波作为底部动力时程,峰值加速度0.2 g(g为重力加深度),如图 5所示。它的强度适中,与Rayleigh波的强度也较为匹配。经过试算,在该地震波作用下,同时激活的Rayleigh波能够产生显著的影响。
|
| t为时间。 图 5 美国加利福尼亚Upland地震波加速度时程曲线(NE155°方向) Figure 5 Acceleration time history curve for seismic waves in Upland, California (in NE155° direction) |
|
|
Rayleigh波作用下不同动力边界条件对场地动力响应的影响研究计算方案见表 2。
| 方案 | 模型尺寸 | 材料模型及参数 | 动力边界 |
| 1 | 100 m×30 m | HSS, α=β=2.5×10-2, C1 =C2 =1.0 | 两侧固定边界 |
| 2 | 100 m×30 m | HSS, α=β=2.5×10-2, C1 =C2 =1.0 | 两侧黏性边界;底部固定边界 |
| 3 | 100 m×30 m | HSS, α=β=2.5×10-2, C1 =C2 =1.0 | 两侧自由场边界;底部固定边界 |
| 4 | 100 m×30 m | HSS, α=β=2.5×10-2, C1 =C2 =1.0 | 远离激励侧黏性边界;激励侧固定边界 |
| 5 | 100 m×30 m | HSS, α=β=2.5×10-2, C1 =C2 =2.0 | 远离激励侧黏性边界;激励侧固定边界 |
| 6 | 100 m×30 m | HSS, α=β=2. 5×10-2, C1 =C2 =2.0 | 远离激励侧黏性边界;激励侧固定边界 |
| 7 | 100 m×30 m | MC, α=β=2.5×10-2, C1 =C2 =1.0 | 远离激励侧黏性边界;激励侧固定边界 |
| 8 | 100 m×100 m×30 m | HSS, α=β=2.5×10-2, C1 =C2 =1.0 | 远离激励侧黏性边界;激励侧固定边界 |
| 注:方案1—7为二维模型,模型尺寸为长×宽;方案8为三维模型,模型尺寸为长×宽×高。MC为摩尔库伦模型。 | |||
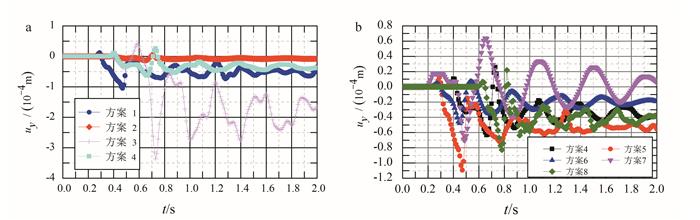
以二维应变模型中心监测点B(50,0)为例,输出其在Rayleigh波作用下随动力作用时间的动力响应曲线,如图 6所示。
|
| a.方案1—4的竖向位移-动力时间曲线;b.方案4—8的竖向位移-动力时间曲线。t为时间。 图 6 Rayleigh波作用下不同方案时平面模型监测点B(50, 0)动力响应曲线 Figure 6 Dynamic response curves for the monitoring site B(50, 0) in a planar model with different calculation schemes under the effects of Rayleigh waves |
|
|
从图 6a可以看出:对于Rayleigh波采用两侧自由场边界(方案3)时,uy-t曲线震荡非常大,但能量经过传播后,耗散较慢;采用两侧黏性边界(方案2)时,过大吸收荷载激励的耗散导致传递到监测点位置的波能量很小,uy仍在0左右小幅波动;采用两侧固定边界(方案1)和激励侧固定边界另一侧黏性边界(方案4)时,可以看到波的初次到达相差不大(约0.1 s);而后的震荡过程中,方案4波动较小,具有更好的收敛性,能够在Rayleigh波的动力分析中获得更好的场地响应。因此,将方案4的边界称为优化边界条件。
在采用优化边界条件下,分别考虑松弛系数变化(方案5)、Rayleigh阻尼变化(方案6)、土体为摩尔库伦(MC)本构模型(方案7)以及三维模型(方案8)的情况,与方案4得到的监测点B(50,0)竖向位移时程曲线共同绘于图 6b。
通过图 6b可以看出:动力边界松弛系数(方案5)变化对场地动力响应影响较小;增大地基的材料阻尼系数β(方案6)使得其动力响应振幅减小且衰减速度更快;采用MC材料本构模型(方案7)时由于没有滞回阻尼导致振荡幅度过大、衰减缓慢;三维(方案8)与二维模型结果体现的场地动力响应规律一致。
综上所述,在Rayleigh波作用下,采用本文所提的优化边界,不会使过大的吸收荷载激励导致能量衰减过快,能考虑到动力作用的震荡效应,又能较好地收敛,具有较好的动力响应结果。
4 Rayleigh波+底部地震波激励共同作用下动力边界影响分析 4.1 计算方案Rayleigh波和地震波共同作用下不同动力边界条件对场地动力响应的影响研究计算方案见表 3。其中底部地震波采用美国加利福尼亚Upland地震波加速度时程(图 5)。
| 方案 | 模型尺寸 | 激励荷载 | 动力边界 |
| 9 | 100 m×30 m | Rayleigh波+底部加速度时程 | 两侧黏性边界;底部柔性地基边界 |
| 10 | 100 m×30 m | Rayleigh波+底部加速度时程 | 两侧自由场边界;底部柔性地基边界 |
| 11 | 150 m×30 m | Rayleigh波+底部加速度时程 | 两侧自由场边界;底部柔性地基边界 |
| 12 | 50 m×30 m | Rayleigh波+底部加速度时程 | 两侧自由场边界;底部柔性地基边界 |
| 13 | 100 m×100 m×30 m | 底部加速度时程 | 激励左右两侧自由场边界;其余侧固定边界 |
| 注:方案9—12为二维模型,模型尺寸为长×宽;方案13为三维模型,模型尺寸为长×宽×高。 | |||
场地水平加速度ax(以g表示)的云图如图 7所示。
|
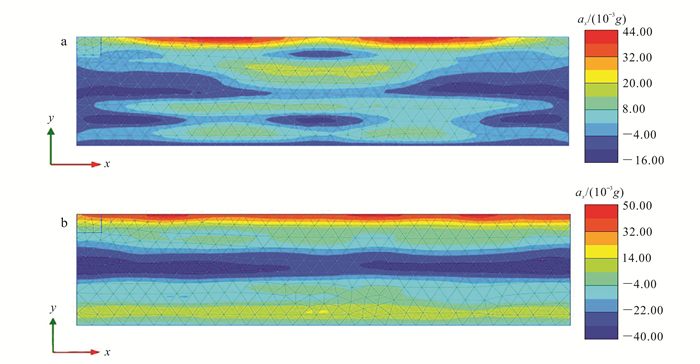
| a.方案9;b.方案10。 图 7 Rayleigh波+地震波作用下场地水平加速度云图 Figure 7 Cloud chart for horizontal acceleration of site under the effects of Rayleigh waves and seismic waves |
|
|
从图 7可以看出:采用黏性边界(图 7a)时,场地水平加速度响应不成层,此外,模型两侧边界效应明显;采用自由场边界(图 7b)时,场地水平加速度响应表现出较规律的成层性分布特征,且模型两侧边界无明显的过度吸收或者能量反射现象。
以位于模型表面中心的监测点B(50, 0)为例,将两侧黏性边界(方案9)、两侧自由场边界(方案10)、模型长度增大(方案11)和减小(方案12)4种情况下的点B水平位移时程曲线、加速度频谱和PSA峰值共同绘于图 8。
|
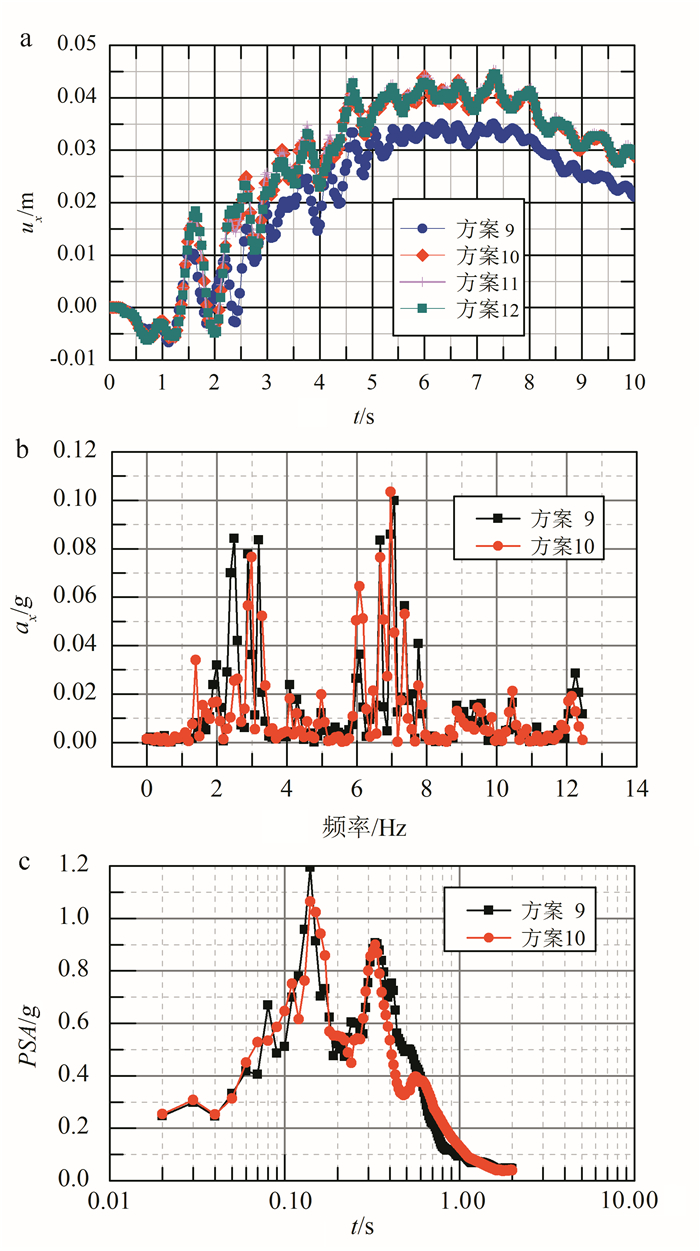
| a.水平位移-时间曲线;b.水平加速度频谱曲线;c.水平加速度PSA曲线。 图 8 Rayleigh波+地震波作用下点B(50, 0)动力响应曲线 Figure 8 Horizontal displacement-time curve for B (50, 0) under the effects of rayleigh dynamic response waves |
|
|
从图 8可知:模型两侧采用自由场边界时,无论模型水平尺寸取与黏性边界模型尺寸相同,还是比之更大或更小的模型尺寸时,自由场边界下的点B水平位移都比黏性边界下的点B水平位移偏大一些(图 8a),进一步表明黏性边界限制了模型内部土体的水平位移;黏性边界(方案9)和自由场边界(方案10)得到的点B响应加速度频谱差别不大(图 8b);黏性边界(方案9)的PSA峰值略大于自由场边界(方案10)(图 8c),这是由于黏性边界吸收不足,一部分波反射叠加引起的;黏性边界计算所得的PSA在0.4 s~0.6 s区间大于自由场边界的计算值,而在0.6 s~1.1 s区间则较小,这也是由边界条件引起的。
在二维和三维模型中,通过不同高度的监测点输出PSA加速度曲线,如图 9所示。
|
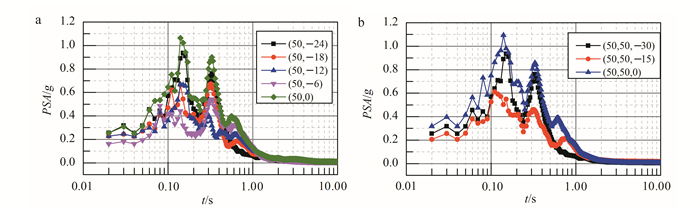
| a.二维;b.三维。 图 9 Rayleigh波+地震波作用下不同高度监测点水平加速度PSA曲线 Figure 9 Horizontal acceleration PSA curves for monitoring sites at different heights under the effects of Rayleigh waves and seismic waves |
|
|
从图 9a可以看出,PSA加速度在0.04 s后逐步被放大,产生一定的波动后,最后减少至0。从图 9b可以看出,在三维模型中存在同样的效果,且中心点(50,50,0)PSA加速度曲线与二维能够很好地对应。
5 Rayleigh波+底部地震波共同作用下动力边界优化组合效果分析 5.1 计算方案通过前述分析可知,单独设置黏性边界或自由场边界,能够在一定程度上实现波在模型边界上的传播和对反射的吸收,但效果还不够理想。下面主要通过三维计算模型,研究Rayleigh波+底部地震波双动力输入作用下,采用黏性边界、自由场边界及固定边界的组合设置人工边界条件,研究土体本构为线弹性及弹塑性(如小应变硬化模型HSS)的综合管廊对场地动力响应的影响,具体组合计算方案及边界条件见表 4、表 5。
| 方案 | 模型尺寸 | 激励荷载 | 动力边界组合 |
| 14 | 100 m×100 m×30 m | Rayleigh波 | 激励侧固定边界,远离激励侧黏性边界,其余两侧自由场边界 |
| 15 | 100 m×100 m×30 m | 底部加速度时程 | |
| 16 | 100 m×100 m×30 m | Rayleigh波+底部加速度时程 | |
| 注:方案14—16均为三维模型,模型尺寸为长×宽×高。 | |||
| 方案 | 模型尺寸 | 激励荷载 | 动力边界组合 |
| 17 | 100 m×100 m×30 m | Rayleigh波 | 激励侧固定边界,远离激励侧黏性边界,其余两侧自由场边界 |
| 18 | 100 m×100 m×30 m | 底部加速度时程 | |
| 19 | 100 m×100 m×30 m | Rayleigh波+底部加速度时程 | |
| 注:方案17—19均为三维模型,模型尺寸为长×宽×高。 | |||
土体为线弹性模型时,Rayleigh波+底部加速度时程(方案16)共同作用下不同时刻的变形网格如图 10所示。不同本构模型、不同边界、不同动力作用下点A(50, 50, 0)的竖向位移时程曲线如图 11所示。考虑土体弹塑性模型(HSS)条件下,底部地震波作用(方案18)下地基水平加速度云图如图 12所示。
|
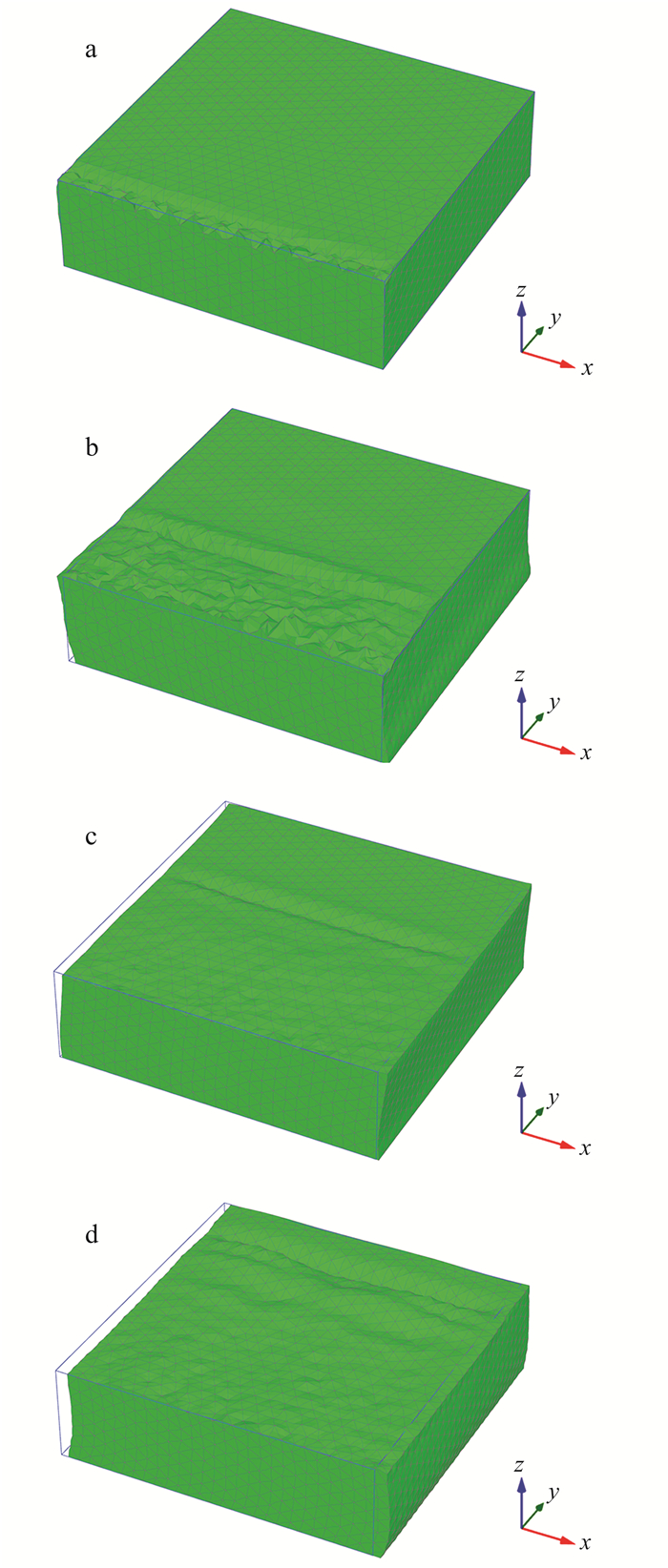
| a.t=2.14 s;b.t=2.40 s;c. t =2.66 s;d. t=2.92 s。 图 10 Rayleigh波+底部地震波共同作用下在不同时刻网格变形特征 Figure 10 Mesh deformation characteristics under the effects of Rayleigh waves and bottom seismic waves at different times |
|
|

|
| a.线弹性模型;b. HSS模型。 图 11 Rayleigh波+底部地震波共同作用下点A(50, 50, 0)的竖向位移时程曲线 Figure 11 Vertical displacement time history curve for A (50, 50, 0) under the effects of Rayleigh waves and bottom seismic waves |
|
|
|
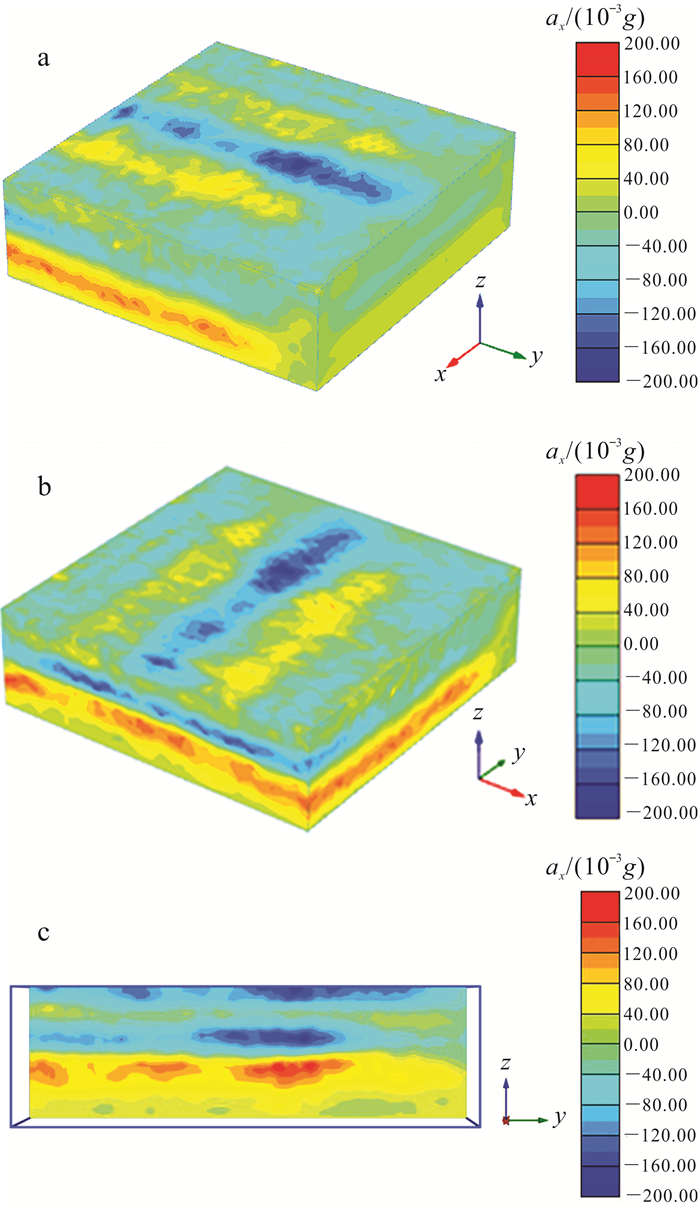
| a.三维ax云图,t =1.10 s,视角1;b.三维ax云图,t=1.10 s,视角2;c.剖面ax云图,t =1.10 s。a、b图中,axmax=0.192 2g(单元14472在节点23474),axmin=-0.192 7g(单元27662在节点26433)。 图 12 优化动力边界下地基水平加速度云图 Figure 12 Cloud chart for horizontal acceleration of foundation in optimized dynamic boundary conditions |
|
|
由图 10可以看出,当地基为线弹性体时,Rayleigh波和底部地震波的交叉干扰较少,Rayleigh波和底部地震波共同作用时均能够得到较好的传播,在模型边界上能够得到恰当的吸收和释放,表明了此时边界条件设置是有效的。图 11a显示,底部加速度时程(方案15)引起的模型表面中心点竖向位移基本可忽略;而单独Rayleigh波作用下(方案14)与双动力(Rayleigh波+底部加速度时程)输入作用下(方案16)的该中心点的竖向位移基本一致,进一步表明线弹性条件下,使用该动力边界,Rayleigh波与底部地震波引起的场地动力响应相互干扰很小,近似为线性叠加。
从图 11b可以看出,Rayleigh波(方案17)引起的模型表面中心点竖向位移很小,底部地震波(方案18)引起的竖向位移占主导,双动力输入下(方案19)该中心点的竖向位移基本可视为Rayleigh波和地震波作用效果的线性叠加。这是由于HSS模型能够反映土体的滞回阻尼特性,土体塑性变形随着动力作用时间的推进产生了一定的累积增长,模型表面中心监测点竖向位移时程曲线的形态与弹性地基条件下有明显差别。
对于类似HSS本构模型的弹塑性材料地基而言,分析Rayleigh波+底部地震波共同作用下的动力响应,采用上述边界条件下也同样适用。从图 12可以看出:对于考虑土体小应变特性的弹塑性地基,计算模型y方向的最小值ymin(即激励侧)未设动力人工边界,波的传播受影响不大,加速度仍较大(云图中蓝色区域较大);但是计算模型y方向的最大值ymax(即远离激励侧)设置了黏性边界,在边界附近加速度快速衰减,(云图中蓝色区域几乎没有)可见黏性边界造成了一定范围内的能量吸收。
综上所述,Rayleigh波和地震波这两种动力输入引起的场地动力响应(位移和加速度)可以按线性叠加处理,二者交叉干扰较小;从动力人工边界的影响来看,黏性边界对地震波引起的动力响应有一定范围的吸收,自由场边界对Rayleigh波引起的动力响应也有一定范围的变形限制影响。在Rayleigh波和底部加速度时程共同作用下,可采用激励侧固定边界、远离激励侧黏性边界、其余两侧自由场边界的优化动力边界。
6 结论1) 黏性边界主要考虑对外行波的吸收效果,而没有考虑地震动的输入问题,在地震波(底部水平加速度时程)作用下,黏性边界会对模型内部土体的水平位移产生限制作用而使得场地内水平位移响应偏小,自由场边界则基本不存在这种限制作用,更适用于底部加速度时程引起的动力响应分析。
2) 黏性边界仅考虑了对散射波能量的吸收,并未考虑人工边界外半无限介质的弹性恢复性能,在Rayleigh波作用下,黏性边界对散射能量的吸收效果偏大,导致场地动力响应偏小,而采用自由场边界时则表现出明显偏大的强烈振荡。相比之下,采用激励侧固定边界、另一侧黏性边界的组合动力边界设置能够得到较好的场地动力响应结果,具有较好的收敛性。
3) 基于激励侧固定边界、远离激励侧黏性边界、其余侧自由场边界的优化组合动力边界设置,在Rayleigh波和底部加速度时程共同作用下,二者引起的动力响应交叉干扰较少,可按线性叠加处理;同时,黏性边界对地震波引起的动力响应有一定范围的吸收,自由场边界对Rayleigh波引起的动力响应也有一定范围的变形限制影响。
4) 计算Rayleigh波和底部加速度时程共同作用下,弹塑性地基的综合管廊地震动力响应,边界条件可设置为:激励侧固定边界、远离激励侧黏性边界、其余侧自由场边界。
| [1] |
城市综合管廊工程技术规范: GB 50838-2015[S]. 北京: 中国建筑工业出版社, 2015.
Technical Code for Urban Utility Tunnel Engineering: GB 50838-2015[S]. Beijing: China Architecture & Building Press, 2015. |
| [2] |
庄海洋, 程绍革, 陈国兴. 阪神地震中大开地铁车站震害机制数值仿真分析[J].
岩土力学, 2008, 29(1): 245-250.
Zhuang Haiyang, Cheng Shaoge, Chen Guoxing. Numerical Simulation and Analysis of Earthquake Damages of Dakai Metro Station Caused by Kobe Earthquake[J]. Rock & Soil Mechanics, 2008, 29(1): 245-250. |
| [3] | Wolf J P, Song C. Some Cornerstones of Dynamic Soil-Structure Interaction[J]. Engineering Structures, 2002, 24(1): 13-28. DOI:10.1016/S0141-0296(01)00082-7 |
| [4] |
邱流潮, 金峰. 地震分析中人工边界处理与地震动输入方法研究[J].
岩土力学, 2006, 27(9): 1501-1504.
Qiu Liuchao, Jin Feng. Study on Method of Earthquake Input and Artificial Boundary Conditions for Seismic Soil-Structure Interaction Analysis[J]. Rock & Soil Mechanics, 2006, 27(9): 1501-1504. |
| [5] | Hatzigeorgiou G D, Beskos D E. Soil-Structure In-teraction Effects on Seismic Inelastic Analysis of 3-D Tunnels[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(9): 851-861. DOI:10.1016/j.soildyn.2010.03.010 |
| [6] | Ghandil M, Behnamfar F. The Near-Field Method for Dynamic Analysis of Structures on Soft Soils Including Inelastic Soil-Structure Interaction[J]. Soil Dynamics and Earthquake Engineering, 2015, 75: 1-17. DOI:10.1016/j.soildyn.2015.03.018 |
| [7] |
张波, 李术才, 杨学英, 等. 三维黏弹性介质人工边界研究[J].
岩土力学, 2009, 30(11): 3469-3475.
Zhang Bo, Li Shucai, Yang Xueying, et al. Study of Three Dimensional Viscoelastic Medium Artificial Boundary[J]. Rock & Soil Mechanics, 2009, 30(11): 3469-3475. DOI:10.3969/j.issn.1000-7598.2009.11.042 |
| [8] |
高峰, 关宝树. 沉管隧道三维地震反应分析[J].
兰州交通大学学报, 2003, 22(1): 6-10.
Gao Feng, Guan Baoshu. Three-Dimensional Seismic Response Analysis of Immersed Tunnel[J]. Journal of Lanzhou Jiaotong University, 2003, 22(1): 6-10. |
| [9] |
孙海峰, 景立平, 孟宪春, 等. ABAQUS中动力问题边界条件的选取[J].
地震工程与工程振动, 2011, 31(3): 71-76.
Sun Haifeng, Jing Liping, Meng Xianchun, et al. The Selection of Boundary Conditions in Dynamic Problems by Using ABAQUS[J]. Journal of Earthquake Engineering & Engineering Vibration, 2011, 31(3): 71-76. |
| [10] |
刘志强, 孙建国, 孙辉, 等. 曲线坐标系下的完全匹配层吸收边界条件[J/OL]. 吉林大学学报(地球科学版) (2017-03-23)[2017-09-28]. http://kns.cnki.net/kcms/detail/22.1343.p.20170323.1418.002.html.
Liu Zhiqiang, Sun Jianguo, Sun Hui, et al. A Perfectly Matched Layer Absorbing Boundary Condition Under the Curvilinear Coordinate System[J/OL]. Journal of Jilin University (Earth Science Edition), (2017-03-23)[2017-09-28]. http://kns.cnki.net/kcms/detail/22.1343.p.20170323.1418.002.html. http://xuebao.jlu.edu.cn/dxb/CN/abstract/abstract10748.shtml |
| [11] | Jiao Y Y, Zhang X L, Zhao J, et al. Viscous Bou-ndary of DDA for Modeling Stress Wave Propagation in Jointed Rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(7): 1070-1076. DOI:10.1016/j.ijrmms.2007.03.001 |
| [12] | Deeks A, Randolph M. Axisymmetric Time-Domain Transmitting Boundaries[J]. Journal of Engineering Mechanics, 1994, 120(1): 25-42. DOI:10.1061/(ASCE)0733-9399(1994)120:1(25) |
| [13] |
刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法[J].
土木工程学报, 1998, 31(3): 55-64.
Liu Jingbo, Lü Yandong. A Direct Method for Analysis of Dynamic Soil-Structure Interaction[J]. China Civil Engineering Journal, 1998, 31(3): 55-64. |
| [14] |
刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J].
工程力学, 2005, 22(6): 46-51.
Liu Jingbo, Wang Zhenyu, Du Xiuli, et al. Three-Dimensional Visco-Elastic Artificial Boundaries in Time Domain for Wave Motion Problems[J]. Engineering Mechanics, 2005, 22(6): 46-51. |
| [15] |
谷音, 刘晶波, 杜义欣. 三维一致粘弹性人工边界及等效粘弹性边界单元[J].
工程力学, 2007, 24(12): 31-37.
Gu Yin, Liu Jingbo, Du Yixin. 3D Consistent Viscous-Spring Artificial Boundary and Viscous-Spring Boundary Element[J]. Engineering Mechanics, 2007, 24(12): 31-37. DOI:10.3969/j.issn.1000-4750.2007.12.006 |
| [16] |
张燎军, 张慧星, 王大胜, 等. 黏弹性人工边界在ADINA中的应用[J].
世界地震工程, 2008, 24(1): 12-16.
Zhang Liaojun, Zhang Huixing, Wang Dasheng, et al. The Application of Artificial Viscous-Spring Boundary in ADINA[J]. World Earthquake Engineering, 2008, 24(1): 12-16. |
| [17] |
蒋新新, 李建波, 林皋. 边坡场地条件下粘弹性人工边界模型的地震输入模式研究[J].
世界地震工程, 2013, 29(4): 126-132.
Jiang Xinxin, Li Jianbo, Lin Gao. Study on the Seismic Input Mode of Viscoelastic Artificial Boundary Under the Condition of Slope Site[J]. World Earthquake Engineering, 2013, 29(4): 126-132. |
| [18] |
朱志辉, 余志武, 吴方伯, 等. 考虑衰减波特性的透射边界及其实现[J].
湖南大学学报(自然科学版), 2007, 34(12): 1-5.
Zhu Zhihui, Yu Zhiwu, Wu Fangbo, et al. Research on the Artificial Boundary in the Soil-Structure Dynamic Interaction[J]. Journal of Hunan University (Natural Sciences), 2007, 34(12): 1-5. |
| [19] | Liu J, Lu Y. A Direct Method for Analysis of Dynamic Soil-Structure Interaction Based on Interface Idea[J]. Developments in Geotechnical Engineering, 1998, 83(3): 261-276. |
| [20] |
权登州, 王毅红, 井彦林, 等. 黄土区地铁车站动力分析中的无限元传输边界[J].
西安建筑科技大学学报(自然科学版), 2015, 47(4): 537-542.
Quan Dengzhou, Wang Yihong, Jing Yanlin, et al. Infinite-Element Transmitting Boundary in Dynamic Analysis of Subway Station in Loess Area[J]. Journal of Xi'an University of Architecture & Technology (Natural Science Edition), 2015, 47(4): 537-542. |
| [21] | Seed H B, Martin P P, Lysmer J. The Generation and Dissipation of Pore Water Pressures During Soil Liquefaction[R]. Oakland: University of California, 1975. |
| [22] |
付晓东, 盛谦, 张勇慧. DDA方法中的人工边界问题研究[J].
岩石力学与工程学报, 2015, 34(5): 986-993.
Fu Xiaodong, Sheng Qian, Zhang Yonghui. Investigation on Artificial Boundary Problem in Discontinuous Deformation Analysis Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 986-993. |
| [23] |
铁路工程抗震设计规范GB50111-2006[S]. 北京: 中国计划出版社, 2006.
Code for Seismic Design of Railway Engineering: GB50111-2006[S]. Beijing: China Planning Press, 2006. |
| [24] |
建筑抗震设计规范GB50011-2001[S]. 北京: 中国建筑工业出版社, 2001.
Code for Seismic Design of Building GB50011-2010[S]. Beijing: China Architecture & Building Press, 2001. |
| [25] | Lamb H. On the Propagation of Tremors over the Surface of an Elastic Solid[J]. Philosophical Transactions of the Royal Society of London, 1904, 203, 359: 1-42. |
| [26] | Shi Youzhi. Contribution of Rayleigh Damping Para-meters to Site Response Under Influence of Rayleigh Wave[J]. Revista Tecnica De La Facultad De Ingenieria Universidad Del Zulia, 2016, 39(6): 48-59. |


