0 引言
滑坡地质灾害危害严重,因此其一直都引起世界各国学者的关注,多年来研究人员对于滑坡的研究从未间断。滑坡的分类在认识滑坡形成机理和治理过程中具有非常重要的意义[1],滑坡的破坏类型多种多样,一般按滑坡的受力状态可分为牵引式滑坡和推移式滑坡[2],以及具有两者特点的复合式滑坡。其中:牵引式滑坡由于前缘受库水位冲刷或人工开挖形成由前至后的变形破坏[3-10];推移式滑坡由于后缘常年加载及降雨作用影响导致由后至前的变形破坏[11-17];复合式滑坡由于前缘关键阻滑段缺失以及后缘加载效应致使形成由前后至中间的变形破坏[18-21]。因此,准确认识滑坡的变形破坏模式、确定滑坡的变形破坏类型在工程中尤为重要,是不同类型滑坡定性、定量分析及防护治理的前提。
很多学者对滑坡进行了长期的研究发现,边坡变形破坏是一个渐变的过程:Quinn等[22]和Dey等[23]分别采用断裂力学原理和大变形有限元建模方法对敏感性黏土边坡渐进式破坏过程进行了分析;王庚荪等[24]和刘忠玉等[25]提出了一个具有应变软化性质的土质边坡渐进破坏力学模型,分析了边坡稳定性变化情况;刘开富等[26]依据大变形的分岔理论采用D-P屈服准则研究了边坡剪切带位置及扩展情况,并进行了变形渐进破坏稳定性分析;唐芬等[27]进行了土坡渐进破坏的双安全系数的讨论;刘爱华等[28]首次提出了平面渐进破坏模型,并给出了该模型的稳定性计算方法;余飞等[29]采用了基于接触单元模型的数值模拟方法,探讨了顺层岩质高斜坡渐进变形失稳机制;朱雷等[30]提出了基于滑带强度参数动态演化的滑坡稳定性评价方法,研究了滑坡力学参数与稳定性的动态变化过程;卢应发等[31-32]在对滑坡渐进变形分析的基础上,提出了几种新的滑坡稳定性系数计算方法;凌道盛等[33]基于黏聚区域模型及强化有限单元法,提出了一种剪切带渐进扩展过程模拟的有限元分析方法,模拟了剪切带的应变软化特性;何忠明等[34]基于应变软化模型采用FLAC3D软件研究了软岩边坡开挖过程中及支护后的稳定性变化规律;薛海斌等[35]通过研究验证了基于矢量和法和基于等效强度参数的极限平衡法,分析了应变软化边坡稳定性的合理性与可靠性。综上,在滑坡渐进破坏过程中,滑带的性质对滑坡的稳定性具有控制作用,并将对抗滑工程设计产生很大影响。
在现有工程的滑坡推力计算过程中,为了让计算得以简化,滑带的强度参数都是统一取值,这与大部分滑坡实际不相符。本文通过不同类型滑坡渐进破坏过程的研究,基于滑带参数弱化特征进行不同类型滑坡推力的计算,提出了滑带参数的合理取值方法,以期为进行合理的防治工程设计提供理论依据。
1 滑坡变形破坏模式 1.1 牵引式滑坡变形破坏模式牵引式滑坡的坡脚是重要的阻滑段,经过人工开挖或者河流冲刷,加上持续降雨作用,斜坡前缘临空高度增加,产生剪应力集中效应,导致滑坡前缘首先变形;滑坡前缘变形将对其后部坡体产生牵引效应,使得关键阻滑段缺失,支撑削弱甚至临空,进而使中后部坡体产生应力集中效应,潜在滑动面变形而产生应力损伤,导致后部滑体变形;随着变形逐步向后向上发展,形成受前缘阻滑段渐变式牵引变形控制、中后段逐步变形破坏的链式传递过程,表现为后退式渐进破坏模式(图 1)。
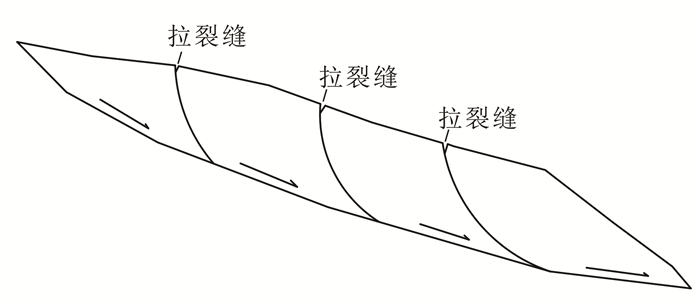
|
| 图 1 牵引式滑坡破坏模式图 Figure 1 Deformation and failure model of retrogressive landslide |
|
|
推移式滑坡由于后缘常年加载,后缘张开裂缝发育,后缘滑体荷载不断积累,触发了滑坡的变形,引起后部失稳始滑;滑坡后缘滑动带向下扩展,随着塑性区的扩大,应力集中范围向前部扩大,并逐渐向前缘积累,局部产生鼓胀裂缝。变形具有由后至前传递的特征,而前缘较平缓的滑坡区域有效地阻挡了后缘所传递的变形量;但当前缘滑体所提供的抗滑力不足以维持后缘所施加的下滑力时,滑动面由上至下逐渐贯通,从而导致滑坡整体失稳破坏,表现为前进式渐进破坏模式(图 2)。

|
| 图 2 推移式滑坡破坏模式图 Figure 2 Deformation and failure model of load-caused landslide |
|
|
复合式滑坡同时具有牵引式滑坡和推移式滑坡的特点,变形始于前缘和后缘坡体,引起后部失稳始滑而推动中部滑动,以及前部关键阻滑段缺失而牵引中部滑动;这样将导致塑性区由上下逐渐向中间贯通,随着塑性区的扩大,当整个滑动面空间贯通时,滑坡就开始整体滑移,表现为由上下至中间复合式渐进破坏模式(图 3)。
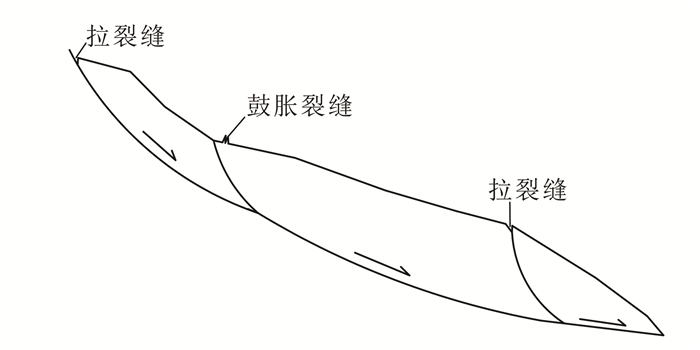
|
| 图 3 复合式滑坡破坏模式图 Figure 3 Deformation and failure model of combined landslide |
|
|
滑坡力的传递与岩土体的力学特性紧密相关[31]。滑坡的演化规律遵循量变到质变的过程,也即滑坡渐进破坏的过程[36]。渐进性破坏一般源于岩土材料的应变软化效应,因此,本文对滑带的研究都是基于材料应变软化这一特性展开。对于具有应变软化属性的滑带,其力学强度基本都经历峰前应力阶段、软化阶段和残余应力阶段(图 4)。大量试验表明,对于应变软化的岩土体,当岩土体承受的剪切力达到最大剪切强度后,随着岩土体连续的变形而发生剪切破坏,岩土体的抗剪强度便降到残余强度。
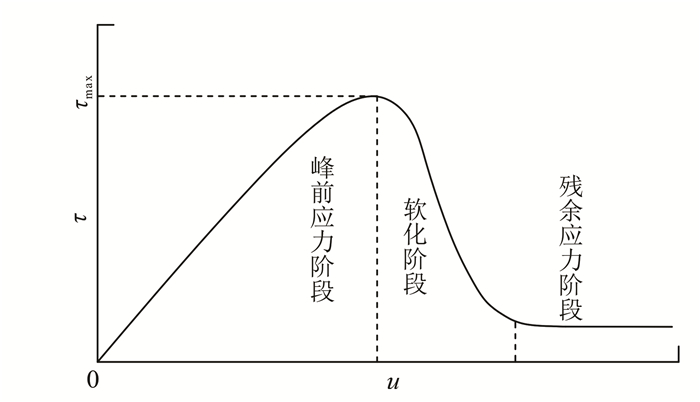
|
| τ为岩土体剪应力;τmax为岩土体最大剪应力;u为岩土体剪切位移。 图 4 滑带本构曲线 Figure 4 Constitutive curves of sliding zone |
|
|
滑坡的演化规律遵循量变到质变的规律,滑坡渐进破坏的实质是滑带的力学参数弱化的过程[34]。滑坡渐进破坏过程主要表现在2个方面:在空间上,滑带参数弱化是逐步产生发展的,不同部位滑带的力学参数存在差异性;在时间上,滑带力学参数随着滑坡演化发展而呈现不同的速率弱化。
斜坡破坏是坡体累积变形发展的最终状态[37]。根据滑带力学参数弱化过程,可以从宏观上刻画滑带在空间上存在的峰前应力、临界应力、残余应力3种状态。滑坡在整个演化过程中,在二维平面内一般只有一点处于峰值应力状态[31]。为了更清晰地解析滑坡渐进破坏过程,对3种类型滑坡渐进式演化过程进行分析。
1) 牵引式滑坡:在整个渐进演化过程中,当某条块下滑力等于抗滑力时,该滑坡条块一般处于临界状态;处于该条块之前的条块为残余应力状态条块即发生剪切破坏,处于该条块之后的条块处于峰前应力状态条块即未发生剪切破坏。临界状态位置随着渐进破坏过程而逐渐向上移动(图 5)。
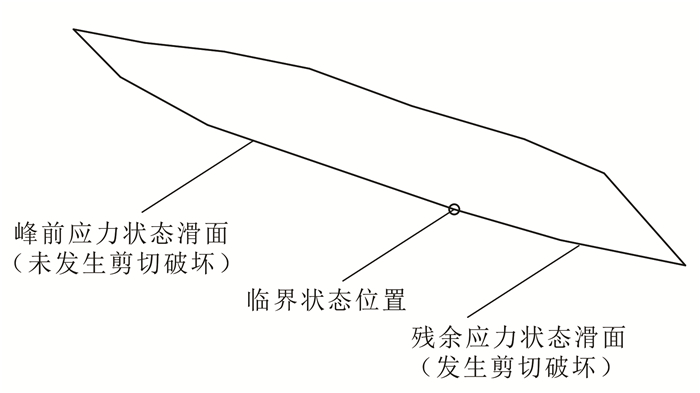
|
| 图 5 牵引式滑坡渐进演化过程图 Figure 5 Progressive failure process of retrogressive landslide |
|
|
2) 推移式滑坡:在整个渐进演化过程中,当某条块下滑力等于抗滑力时,该滑坡条块一般处于临界状态;处于该条块之前的条块为峰前应力状态条块即未发生剪切破坏,处于该条块之后的条块处于残余应力状态条块即发生剪切破坏。临界状态位置随着渐进破坏过程而逐渐向下移动(图 6)。
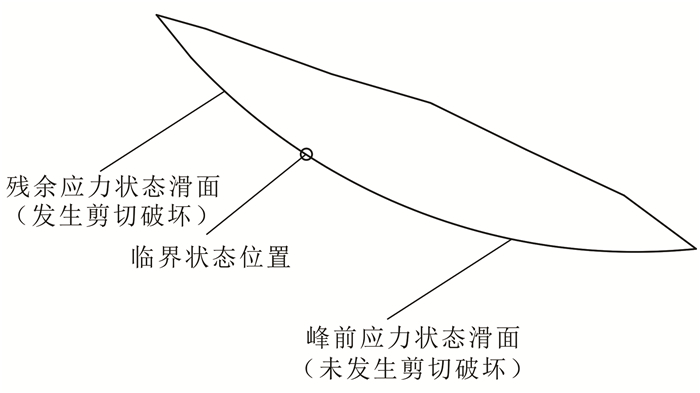
|
| 图 6 推移式滑坡渐进演化过程图 Figure 6 Progressive failure process of load-caused landslide |
|
|
3) 复合式滑坡:复合式滑坡渐进破坏过程较为复杂,一般情况下,临界状态位置有2个,前部的临界条块定义为第一临界状态条块,后部的临界条块定义为第二临界状态条块。第一临界状态条块前部和第二临界状态条块后部的条块处于残余应力状态条块即发生剪切破坏;第一临界状态条块和第二临界状态条块之间的条块处于峰值应力状态条块即未发生剪切破坏。临界状态位置随着渐进破坏过程而逐渐由前后向中间移动(图 7)。

|
| 图 7 复合式滑坡渐进演化过程图 Figure 7 Progressive failure process of combined landslide |
|
|
基于滑带参数弱化特征,并且在临界状态下满足摩尔-库伦准则条件,假设滑坡的第m条块为临界状态条块,判别条件如下:假设第m条块为临界状态条块,则其抗滑力等于下滑力。这里对不同类型的滑坡分别进行判别。
1) 牵引式滑坡
牵引式滑坡是后退式渐进破坏过程,其临界状态条块是逐渐向后递进的;因此,第m条块之上的1~(m-1)条块处于峰前应力状态而未发生剪切破坏,即稳定条块(即第m-1条块的剩余下滑力Em-1 = 0),则第m条块为临界状态条块的判别标准为
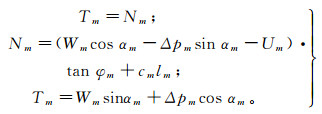 (1)
(1) 式中:Δpm=pm-pm′,pm为第m条块上边静水压力的合力,pm′为第m条块下边静水压力的合力,Δpm为第m条块土体两侧静水压力的合力;Tm为第m条块的下滑力;Nm为第m条块的抗滑力;Wm为第m条块的重力;Um为第m条块土体底部孔隙水压力;αm为第m条块滑面倾角;cm为黏聚力;φm为内摩擦角;lm为条块底边长。
2) 推移式滑坡
推移式滑坡是前进式渐进破坏,其临界状态条块是逐渐向前递进的,m条块之上的1~(m-1)条块处于残余应力状态而发生了剪切破坏,即为不稳定条块(Em-1>0);因此m条块受力要考虑上部条块的推力作用,则第m条块为临界状态条块的判别标准为
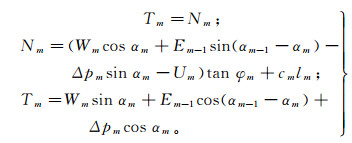 (2)
(2) 3) 复合式滑坡
复合式滑坡是复合式渐进破坏过程,在渐进演化过程中存在两处临界状态条块,两处的临界状态条块判别标准为:第一临界状态条块按牵引式滑坡的确定方法确定;第二临界状态条块按推移式滑坡的确定方法确定。
3 不同类型滑坡推力计算 3.1 不同类型滑坡推力计算公式建立在不平衡推力法的基础上,考虑不同类型滑坡的渐进破坏过程,现在滑坡在演化过程的某一时刻进行条分,并作如下假设:假设滑坡的总条块数为n,对于牵引式滑坡,滑坡从下至上发生剪切破坏,假设第m条块为临界状态条块;对于推移式滑坡,滑坡从上至下发生剪切破坏,假设第k条块为临界状态条块;对于复合式滑坡,滑坡从上下至中间发生剪切破坏,第m条块为第一临界状态条块,第k条块为第二临界状态条块。由于滑带参数对滑坡稳定性起着控制作用,而滑坡设计推力的准确计算又是实现有效治理的前提;因此,基于上述不同类型滑坡的渐进破坏过程分析,在确定工程治理安全等级相同的前提下,本文提出随着渐进破坏过程的滑带参数选择方法,即滑带发生剪切段取残余强度,未发生剪切段取峰值强度。
因此,依次得到在重力作用下考虑渐进破坏过程的牵引式滑坡、推移式滑坡及复合式滑坡推力计算公式分别为:
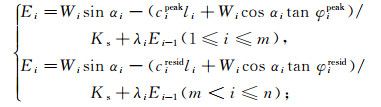 (3)
(3) 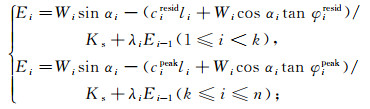 (4)
(4) 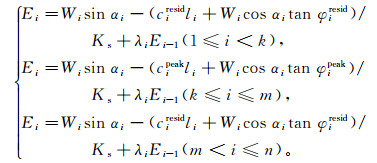 (5)
(5) 其中, 
为了反映不同类型滑坡的渐进演化过程,现以任一个滑坡为例(图 8),对比分析分别产生3种变形破坏模式时滑坡推力变化情况。假设滑坡推力计算参数:滑体容重为21 kN/m3,滑带2种强度参数的取值可参照文献[38-41],本文取滑带的峰值强度参数为黏聚力cpeak=25 kPa、内摩擦角φpeak=18°,滑带的残余强度参数为黏聚力cresid=22.5 kPa、内摩擦角φresid=15°,设计安全系数取1.2,滑体条块数为14。

|
| 1, 2, 3…14为滑块条数。 图 8 滑坡推力计算模型 Figure 8 Thrust calculation model of landslide |
|
|
依据3种类型滑坡的渐进破坏演化过程,结合前面所述方法对其推力进行计算,实现过程分别为:1)滑坡产生牵引式渐进破坏时,2个条块依次从前至后发生剪切破坏,计算得到渐进破坏过程的滑坡设计推力曲线见图 9a;2)对于产生推移式渐进破坏的滑坡,2个条块依次从后向前发生剪切破坏,计算得到渐进破坏过程的滑坡设计推力曲线见图 9b;3)对于产生复合式渐进破坏的滑坡,从前后向中间条块依次发生剪切破坏,计算得到渐进破坏过程的滑坡设计推力曲线见图 9c。

|
| 1.滑坡整体取峰值强度计算结果,2-7.滑坡渐进破坏过程计算结果,8.滑坡整体取残余强度计算结果。 图 9 3种类型滑坡推力计算对比图 Figure 9 Thrust contrast curve of three types of landslides |
|
|
从不同类型滑坡设计推力曲线可以看出:
1) 滑坡整体按照峰值强度进行推力计算与滑坡整体按照残余强度进行推力计算得到的设计推力相差很大,在考虑滑坡渐进式破坏过程计算的推力一般在前两者之间;说明针对具有应变软化的滑坡,如果按照峰值强度进行设计计算的话将产生安全隐患,达不到治理的目的,如果滑坡未发生整体破坏而仍按照残余强度进行设计计算的话将采用较强的加固措施,造成经济浪费。
2) 对于牵引式滑坡,在由前向后渐进破坏的过程中,滑坡推力从前部至后部由峰值强度计算推力值逐渐增大至残余强度计算推力值;对于推移式滑坡,在由后向前渐进破坏过程中,滑坡推力从后部至前部由峰值强度计算推力值逐渐增大至残余强度计算推力值;对于复合式滑坡,在由前后向中间渐进破坏过程中,滑坡推力从前后部至中部由峰值强度计算推力值逐渐增大至残余强度计算推力值。这说明随着渐进破坏过程不同,不同类型滑坡的推力在不断发生不同形式的变化。
3) 假如在某一位置设置抗滑桩工程,对于不同类型的滑坡,在同一位置考虑渐进破坏过程计算得到的设计推力也不同,从图 9中可以看出不同类型滑坡渐进破坏到第5状态时,牵引式滑坡、推移式滑坡和复合式滑坡的推力大小分别为4 100,4 980和3 150 kN/m(图 9);因此,准确把握滑坡的渐进破坏类型在防治工程设计当中也至关重要,是滑坡的有效治理关键。
4) 文中的假设,只是理想状态,更重要的是想说明不同类型滑坡渐进破坏过程及在这个过程中推力变化规律是不同的问题。
4 结论1) 对比分析了牵引式滑坡、推移式滑坡和复合式滑坡3种类型滑坡的变形破坏模式,分别呈现后退式渐进破坏模式、前进式渐进破坏模式和复合式渐进破坏模式。
2) 基于岩土体应变软化性质,阐述滑带性质时空上逐渐软化并呈现峰前应力状态、临界应力状态和残余应力状态;从3种类型滑坡的角度揭示滑坡的渐进演化过程,即牵引式滑坡的临界状态位置随着渐进破坏过程而逐渐向上移动、推移式滑坡的临界状态位置随着渐进破坏过程而逐渐向下移动、复合式滑坡的临界状态位置随着渐进破坏过程由上下逐渐向中间移动,并提出不同类型滑坡临界状态位置的确定方法。
3) 考虑滑坡的渐进破坏过程,提出了不同类型滑坡的渐进破坏过程推力计算公式及计算过程中滑带强度参数选取方法,并通过实例计算不同渐进演化过程滑坡的推力变化规律。如果滑坡设计推力按照峰值强度进行计算,治理后将出现安全隐患;如果滑坡设计推力按照残余强度进行计算,将造成不必要的工程浪费。进一步说明考虑渐进破坏过程进行推力计算既能够从滑坡抗滑本质出发,合理利用自身抗滑作用,又能够满足滑坡渐进破坏过程中的安全要求,具有明确的理论科学依据。
| [1] |
王恭先.
滑坡学与滑坡防治技术文集[M]. 北京: 人民交通出版社, 2010: 34-42.
Wang Gongxian. Proceedings of Landslide Science and Landslide Prevention Technology[M]. Beijing: China Communications Press, 2010: 34-42. |
| [2] |
郑颖人, 陈祖煜, 王恭先, 等.
边坡与滑坡工程治理[M]. 2版. 北京: 人民交通出版社, 2007: 14-24.
Zheng Yingren, Chen Zuyu, Wang Gongxian, et al. Engineering Treatment of Slope and Landslide[M]. 2nd ed. Beijing: China Communications Press, 2007: 14-24. |
| [3] | Lu Yingfa. Deformation and Failure Mechanism of Slope in Three Dimensions[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2015, 7(2): 109-119. DOI:10.1016/j.jrmge.2015.02.008 |
| [4] |
卢应发, 邓国栋, 杨丽平, 等. 滑坡关键块力学行为及力传递特征和不同应力状态的稳定系数研究[J].
岩石力学与工程学报, 2014, 33(5): 884-891.
Lu Yingfa, Deng Guodong, Yang Liping, et al. Study of Mechanical Behaviors of Key Blocks and Characteristics of Force Transmit and Stability Coefficient of Different Stress States of Landslides[J]. Chinese Journal of Geotechnical Engineering, 2014, 33(5): 884-891. |
| [5] |
宋东日, 任伟中, 沈波, 等. 牵引式滑坡的破坏机制及其加固措施探讨:以某高速公路牵引式滑坡为例[J].
岩土力学, 2013, 34(12): 3587-3593.
Song Dongri, Ren Weizhong, Shen Bo, et al. Discussion on Failure Mechanism of Retrogressive Landslide and Its Reinforcement Measures: Taking a Certain Expressway Retrogressive Landslide for Example[J]. Rock and Soil Mechanics, 2013, 34(12): 3587-3593. |
| [6] |
袁从华, 童志怡, 卢海峰. 牵引式滑坡特征及主被动加固比较分析[J].
岩土力学, 2008, 29(10): 2853-2858.
Yuan Conghua, Tong Zhiyi, Lu Haifeng. Analysis of Characteristics of Retrogressive Landslide and Comparison Between Active and Passive Reinforcements[J]. Rock and Soil Mechanics, 2008, 29(10): 2853-2858. DOI:10.3969/j.issn.1000-7598.2008.10.049 |
| [7] |
周跃峰, 龚壁卫, 胡波, 等. 牵引式滑坡演化模式研究[J].
岩土工程学报, 2014, 36(10): 1855-1862.
Zhou Yuefeng, Gong Biwei, Hu Bo, et al. Evolution Mode of Retrogressive Landslide[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(10): 1855-1862. DOI:10.11779/CJGE201410013 |
| [8] |
蔡文, 曹洪, 罗彦, 等. 强度折减有限元法模拟边坡牵引式破坏过程[J].
岩石力学与工程学报, 2011, 30(增刊2): 3529-3533.
Cai Wen, Cao Hong, Luo Yan, et al. Simulation of Retrogressive Landslide Failure Process by Strength Reduction FEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Sup.2): 3529-3533. |
| [9] | Lin Hungchou, Yu Yuzhen, Li Guangxin, et al. A Simplified Numerical Approach for the Prediction of Rainfall-Induced Retrogressive Landslides[J]. Acta Geologica Sinica, 2016, 90(4): 1471-1480. DOI:10.1111/acgs.2016.90.issue-4 |
| [10] |
谭福林, 胡新丽, 张玉明, 等. 牵引式滑坡推力计算方法研究[J].
岩土力学, 2015, 36(增刊2): 532-538.
Tan Fulin, Hu Xinli, Zhang Yuming, et al. Study on Calculation Method of Retrogressive Landslide Thrust[J]. Rock and Soil Mechanics, 2015, 36(Sup.2): 532-538. |
| [11] |
王宝亮, 彭盛恩, 陈洪凯. 推移式滑坡形成机制的力学演绎[J].
地质灾害与环境保护, 2010, 21(2): 74-77.
Wang Baoliang, Peng Sheng'en, Chen Hongkai. Mechanical Deduction of Formation Mechanism for the Thrust Load Caused Landslide[J]. Journal of Geological Hazards and Environment Preservation, 2010, 21(2): 74-77. |
| [12] |
雍睿, 胡新丽, 唐辉明, 等. 推移式滑坡演化过程模型试验与数值模拟研究[J].
岩土力学, 2013, 34(10): 3018-3027.
Yong Rui, Hu Xinli, Tang Huiming, et al. Model Testing and Numerical Simulation Study of Evolutionary Process of Thrust Load Caused Landslide[J]. Rock and Soil Mechanics, 2013, 34(10): 3018-3027. |
| [13] |
易朋莹, 邓时义, 吕涛, 等. 基于FLAC3D的浮托型推移式滑坡稳定性分析[J].
四川理工学院学报(自然科学版), 2012, 25(2): 60-63.
Yi Pengying, Deng Shiyi, Lü Tao, et al. Analysis of Stability for Floated-Pushed Landslide Based on FLAC3D[J]. Journal of Sichuan University of Science & Engineering (Natural Science Edition), 2012, 25(2): 60-63. |
| [14] | Tang Huiming, Hu Xinli, Xu Cong, et al. A Novel Approach for Determining Landslide Pushing Force Based on Landslide-Pile Interactions[J]. Engineering Geology, 2014, 182: 15-24. DOI:10.1016/j.enggeo.2014.07.024 |
| [15] | Zhang Min, Nie Lei, Xu Yan, et al. A Thrust Load-Caused Landslide Triggered by Excavation of the Slope Toe: A Case Study of the Chaancun Landslide in Dalian City, China[J]. Arabian Journal of Geosciences, 2015, 8(9): 6555-6565. DOI:10.1007/s12517-014-1710-6 |
| [16] |
夏浩, 雍睿, 马俊伟. 推移式滑坡模型试验推力加载方法的研究[J].
长江科学院院报, 2015, 32(1): 112-116.
Xia Hao, Yong Rui, Ma Junwei. Method of Driving Force Loading in Model Test of Landslide Caused by Thrust Load[J]. Journal of Yangtze River Scientific Research Institute, 2015, 32(1): 112-116. |
| [17] |
邬爱清, 丁秀丽, 李会中, 等. 非连续变形分析方法模拟千将坪滑坡启动与滑坡全过程[J].
岩石力学与工程学报, 2006, 29(7): 1297-1303.
Wu Aiqing, Ding Xiuli, Li Huizhong, et al. Numerical Simulation of Startup and Whole Failure Process of Qianjiangping Landslide Using Discontinuous Deformation Analysis Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 29(7): 1297-1303. |
| [18] |
杨光华, 钟志辉, 张玉成, 等. 根据应力场和位移场判断滑坡的破坏类型及最优加固位置确定[J].
岩石力学与工程学, 2012, 31(9): 1879-1887.
Yang Guanghua, Zhong Zhihui, Zhang Yucheng, et al. Identification of Landslide Type and Determination of Optimal Reinforcement Site Based on Stress Field and Displacement Field[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(9): 1879-1887. |
| [19] |
肖林萍, 赵玉光. 复合型滑坡体系统的工程地质勘察及其稳定性分析[J].
工程地质学报, 2002, 10(增刊2): 320-325.
Xiao Linping, Zhao Yuguang. Engineering Geological Exploration and Stability Analysis of Complex Landslip System[J]. Journal of Engineering Geology, 2002, 10(Sup.2): 320-325. |
| [20] |
石豫川, 冯文凯, 刘汉超, 等. 特大多期复合型滑坡稳定性评价及因素敏感性分析[J].
岩土力学, 2004, 25(6): 975-980.
Shi Yuchuan, Feng Wenkai, Liu Hanchao, et al. Stability Evaluation for Giant and Multiple Landslide and Sensitive Analysis Factors[J]. Rock and Soil Mechanics, 2004, 25(6): 975-980. |
| [21] |
谭福林, 胡新丽, 张玉明, 等. 复合式滑坡推力计算方法研究[J].
长江科学院院报, 2016, 33(6): 99-104.
Tan Fulin, Hu Xinli, Zhang Yuming, et al. A Method of Calculating the Thrust of Complex Landslide[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(6): 99-104. |
| [22] | Quinn P E, Diederichs M S, Rowe R K, et al. Development of Progressive Failure in Sensitive Clay Slopes[J]. Canadian Geotechnical Journal, 2012, 49(7): 782-795. DOI:10.1139/t2012-034 |
| [23] | Dey R, Hawlader B, Phillips R, et al. Large Deformation Finite-Element Modelling of Progressive Failure Leading to Spread in Sensitive Clay Slopes[J]. Geotechnique, 2015, 65(8): 657-668. DOI:10.1680/geot.14.P.193 |
| [24] |
王庚荪, 孔令伟, 郭爱国, 等. 含剪切带单元模型及其在边坡渐进破坏分析中的应用[J].
岩石力学与工程学报, 2005, 24(21): 3852-3857.
Wang Gengsun, Kong Lingwei, Guo Aiguo, et al. Element Model with Shear Band and Its Application to Progressive Failure Analysis of Slopes[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(21): 3852-3857. DOI:10.3321/j.issn:1000-6915.2005.21.008 |
| [25] |
刘忠玉, 陈少伟. 应变软化土质边坡渐进破坏的演化模型[J].
郑州大学学报(工学版), 2002, 23(2): 37-40.
Liu Zhongyu, Chen Shaowei. Evolution Model of Progressive Failure of Strain-Softening Soil Slopes[J]. Journal of Zhengzhou University(Engineering Science), 2002, 23(2): 37-40. |
| [26] |
刘开富, 谢新宇, 张继发, 等. 土质边坡的弹塑性应变局部化分析[J].
岩土工程学报, 2008, 30(增刊): 291-294.
Liu Kaifu, Xie Xinyu, Zhang Jifa, et al. Elasticplastic Strain Localization Analysis of Soil Slope[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(Sup.): 291-294. |
| [27] |
唐芬, 郑颖人, 赵尚毅. 土坡渐进破坏的双安全系数讨论[J].
岩石力学与工程学报, 2007, 26(7): 1402-1407.
Tang Fen, Zheng Yingren, Zhao Shangyi. Discussion on Two Safety Factors for Progressive Failure of Soil Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7): 1402-1407. |
| [28] |
刘爱华, 王思敬. 平面坡体渐进破坏模型及其应用[J].
工程地质学报, 1994, 2(1): 1-8.
Liu Aihua, Wang Sijing. Progressive Failure Model for Slope with Plane Sliding Surface and Its Application[J]. Journal of Engineering Geology, 1994, 2(1): 1-8. |
| [29] |
余飞, 陈善雄, 余和平. 顺层岩质边坡渐进破坏及失稳机理的数值模拟研究[J].
岩土力学, 2005, 26(增刊1): 36-40.
Yu Fei, Chen Shanxiong, Yu Heping. Numerical Simulation Study on Progressive Destruction and Failure Mechanism of Bedding Rock Slopes[J]. Rock and Soil Mechanics, 2005, 26(Sup.1): 36-40. |
| [30] |
朱雷, 黄润秋, 王小群, 等. 基于滑带强度参数动态演化的滑坡稳定性研究[J].
岩土力学, 2015, 36(增刊2): 431-437.
Zhu Lei, Huang Runqiu, Wang Xiaoqun, et al. Stability Study of Landslide Based on Dynamic Evolution of Sliding Surface Strength Parameter[J]. Rock and Soil Mechanics, 2015, 36(Sup.2): 431-437. |
| [31] |
卢应发, 杨丽平, 刘德富. 一种新的节理本构模型及几种新的滑坡稳定系数计算方法[J].
岩石力学与工程学报, 2013, 32(12): 2431-2438.
Lu Yingfa, Yang Liping, Liu Defu. A New Joint Constitutive Model and a few New Methods of Stability Coefficient Calculation of Landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(12): 2431-2438. |
| [32] |
卢应发, 黄学斌, 刘德富. 边坡稳定分析条块力-位移法及其应用[J].
岩土力学, 2015, 36(10): 2787-2798.
Lu Yingfa, Huang Xuebin, Liu Defu. Slice Block Force-Displacement Method of Slope Stability Analysis and Its Application[J]. Rock and Soil Mechanics, 2015, 36(10): 2787-2798. |
| [33] |
凌道盛, 涂福彬, 卜令方. 基于黏聚区域模型的边坡渐进破坏过程强化有限元分析[J].
岩土工程学报, 2012, 34(8): 1387-1393.
Ling Daosheng, Tu Fubin, Bu Lingfang. Enhanced Finite Element Analysis of Progressive Failure of Slopes Based on Cohesive Zone Model[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1387-1393. |
| [34] |
何忠明, 吴维, 付宏渊, 等. 基于应变软化模型的软岩高边坡过程稳定性研究[J].
中南大学学报(自然科学版), 2013, 44(3): 1203-1208.
He Zhongming, Wu Wei, Fu Hongyuan, et al. Process Stability of Soft Rock High Slope Based on Strain Softening Model[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 1203-1208. |
| [35] |
薛海斌, 党发宁, 尹小涛, 等. 应变软化边坡稳定性分析方法研究[J].
岩土工程学报, 2016, 38(3): 570-576.
Xue Haibin, Dang Faning, Yin Xiaotao, et al. Stability Analysis Methods for Strain-Softening Slopes[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(3): 570-576. |
| [36] |
邹宗兴, 唐辉明, 熊承仁, 等. 大型顺层岩质滑坡渐进破坏地质力学模型与稳定性分析[J].
岩石力学与工程学报, 2012, 31(11): 2222-2231.
Zou Zongxing, Tang Huiming, Xiong Chengren, et al. Geomechanical Model of Progressive Failure for Large Consequent Bedding Rockslide and Its Stability Analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(11): 2222-2231. DOI:10.3969/j.issn.1000-6915.2012.11.010 |
| [37] |
张倬元, 王士天, 王兰生.
工程地质分析原理[M]. 北京: 地质出版社, 1994: 327-330.
Zhang Zhuoyuan, Wang Shitian, Wang Lansheng. Analyzing Principle of Engineering Geology[M]. Beijing: Geological Publishing House, 1994: 327-330. |
| [38] |
张芳枝, 陈晓平. 东深供水工程风化泥质软岩残余强度特性研究[J].
工程地质学报, 2003, 11(1): 54-57.
Zhang Fangzhi, Chen Xiaoping. The Characteristic of Residual Strength of Soft Clayey Rocks of the East River-Shenzhen Water Supply Project[J]. Journal of Engineering Geology, 2003, 11(1): 54-57. |
| [39] |
田斌, 戴会超, 王世梅. 滑带土结构强度特征及其强度参数取值研究[J].
岩石力学与工程学报, 2004, 23(17): 2887-2892.
Tian Bin, Dai Huichao, Wang Shimei. Strength Characteristics of Soil in Slide Zone and Determination of Its Parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(17): 2887-2892. DOI:10.3321/j.issn:1000-6915.2004.17.007 |
| [40] |
谭文辉, 任奋华, 苗胜军. 峰值强度与残余强度对边坡加固的影响研究[J].
岩土力学, 2007, 28(10): 616-618.
Tan Wenhui, Ren Fenhua, Miao Shengjun. Influence of Parameters of Peak Strength and Residual Strength on the Reinforcement of Slopes[J]. Rock and Soil Mechanics, 2007, 28(10): 616-618. |
| [41] |
洪勇, 岳玉秋, 郑孝玉, 等. 大连滨海粉质黏土剪切力学特性环剪试验[J].
吉林大学学报(地球科学版), 2016, 46(5): 1475-1481.
Hong Yong, Yue Yuqiu, Zheng Xiaoyu, et al. Shear Strength of Silty Clay in Dalian by Ring Shear Tests[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(5): 1475-1481. |



