2. 河北省电力勘测设计研究院, 石家庄 050031;
3. 中国科学院电子学研究所, 北京 100190
2. Hebei Electric Power Design & Research Institute, Shijiazhuang 050031, China;
3. Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China
0 引言
传统探地雷达系统多以单输入单输出(single-input-single-output, SISO)的方式进行探测及目标成像。虽然传统单天线雷达的成像技术具有系统简单、探测工作方便等优点,但由于系统获取的信息量有限,在雷达成像中目标的方位、空间分辨率很难提高[1-2]。在探地雷达成像中,也存在许多技术瓶颈,例如数据处理方法单一、有效探测距离近、成像分辨率低等。另外,常规探地雷达天线受电子器件发展水平的限制,难以实现高保真、理想、超窄时宽脉冲信号的发射,单观测点数据目标成像位置参数存在较大的模糊性,系统对目标空间信息识别能力不足。所以,单输入单输出方法获取到的目标信息量有限,容易受多种因素及干扰影响,成像效果很难再取得本质上的提升与飞跃[3]。
多输入多输出(multiple-input-multiple-output, MIMO)雷达是近年来提出的一种新体制雷达,相比SISO探测系统更加有效地利用了探测系统和目标的时空域信息,改善了目标散射截面(radar cross section, RCS)角度起伏给参数估计带来的负面影响,提高了检测性能和空间分辨力。Tan等[4]为了实现MIMO雷达成像,应用了一种基于加权最小二乘的迭代自适应方法,通过比较最小二乘(least squares, LS)估计算法获得的图像,证明了MIMO阵列多普勒和角度分辨能力高于单输入多输出阵列。Xu等[5]利用自适应超分辨谱估计算法进行MIMO雷达成像,探讨了阵列校正误差存在与否的情况下Capon算法、幅度相位估计(amplitude and phase estimation, APES)等自适应技术的抗干扰能力和分辨性能。Tabrikian[6]研究了MIMO雷达DOA(direction of arrival)估计的Barankin限。王鞠庭等[7]研究了复合高斯杂波背景中MIMO雷达DOA估计的克拉美-罗下界。夏威等[8]研究了APES算法在MIMO算法参数估计中的稳健性。在天线阵列设计、成像模型和成像算法等方面,有学者讨论了超宽带MIMO雷达阵列小空域监视问题,研究理想点目标成像时应用了后向投影算法。韩兴斌等[9]和Li等[10]研究了MIMO雷达体制的分布式多通道雷达成像问题,并针对简单的收发阵列共址直线排列,建立了MIMO雷达二维成像模型。Ma等[11]和Wang等[12]建立了一种垂直收发线阵模式的三维宽带MIMO雷达成像模型,并给出了与之相关的三维成像算法。但这些研究成果并没有显著提高雷达的目标探测性能及成像分辨率,应用技术和算法复杂、控制因素及条件假设多样,均难以实现。因此,寻找新的技术方法研究探地雷达成像势在必行。
在常规探地雷达体系中,为了获得目标空间的高分辨信息,通常都尽可能地提高雷达系统的信号带宽。但是由于系统硬件实现难度的限制,超宽带雷达系统实现复杂度大、成本高、可操作性差,因此以超带宽来实现高分辨的方法成效性较差。另外,相对于探空雷达系统,探地雷达系统中电磁信号的传播路径是具有强衰减和低通特性的地下介质,因此无论采用多宽的超宽带信号,最终可分析的有效信号带宽仍是有限的。无限增大带宽和加大发射功率在探测效率和系统探测性能上的提升是有限的,因此应考虑有效利用有限带宽信号或窄带信号的其他信息来加强目标探测性能。时空信息是MIMO雷达探测系统中重要的信号分析对像。MIMO雷达系统主要利用了目标反射信号多径传播的空间特征,有效地提高了目标探测空间分辨率。本文提出的MIMO探地雷达信号模型是一种基于调制窄带信号及散射点目标模型的目标检测系统。该系统设计使用调制窄带信号作为目标探测信号,并在天线阵列各发射单元上使用正交调制信号来实现波形分集。在数据处理上则利用自适应阵列波束形成技术及逆向成像方法(inverse direction imaging method, IDIM)对目标进行成像。自适应波束形成算法可以根据信号环境的变化自适应高速各阵元的加权因子,达到增强信号同时抑制干扰的目的。
在阵列信号处理中,DOA的稳键估计是关键技术。常规阵列信号的DOA估计受到阵列物理孔径和阵元数固定的限制,估计性能受限,而MIMO雷达发射的正交信号具有分集特性,经过一系列处理后可以扩展阵列的孔径,自由度成几何级数增长,因此能提高DOA估计的性能。基于此,本文提出了基于DOA估计的阵列式探地雷达探测目标成像方法。
1 MIMO-GPR信号模型考虑一个具有NT个发射天线和NR个接收天线的MIMO雷达系统。设s(t)为由阵列发射天线发射出去的基带信号,t为时刻。sm(t)表示第m个发射天线阵元的离散基带信号,该基带信号经由角频率为ω0的载波信号调制并发射出去。为了简便分析逆成像算法的应用性能,所建立的理论仿真模型为均匀背景介质模型,并且只考虑电磁波场的空间扩散特性,不考虑背景介质的强衰减与频散特性。在衰减介质模型中,只需增加介质衰减因子,而以下分析过程和方法仍是有效的。
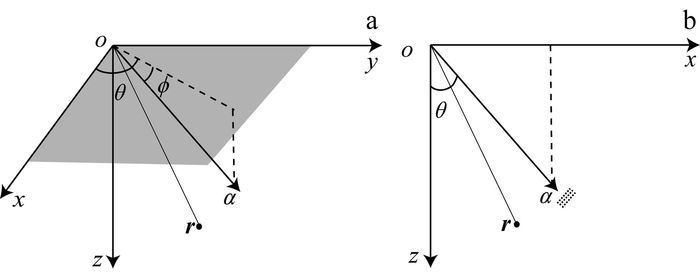
电磁波在空中传播如图 1所示,α为发射阵列探测电磁波的传播方向。在坐标原点位置处,阵列合成平面波可用解析信号表示[13-14]为
|
| 图 1 阵列信号坐标系约定 Figure 1 Array signal coordinate conventions |
|
|
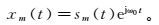 (1)
(1) 式中,j为虚数单位。
在窄带条件下,空间阵列中各阵元采样信号的复包络相同。远场目标位置r处的场值为
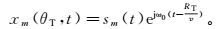 (2)
(2) 式中:θT为电磁波传播方向与z轴的夹角;RT为目标到发射阵元的参考单元距离;v为电磁波的传播速度。
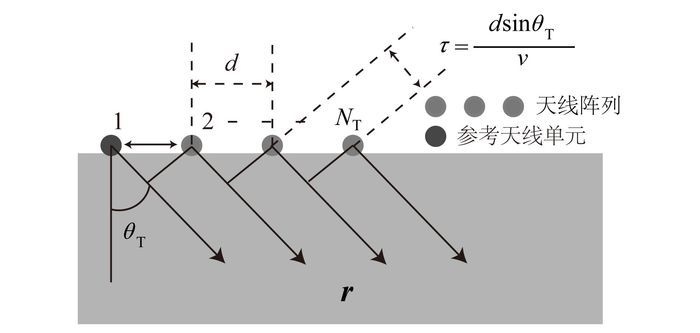
假设NT元天线阵列为均匀线性阵列,相邻阵元间距为d,如图 2所示。设在方向θT处存在散射点目标,目标电磁反射信号幅度为β(θT),则目标散射信号为
|
| 图 2 等距发射线阵几何结构 Figure 2 Geometry of isometric emission line array |
|
|
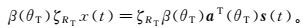 (3)
(3) 式中: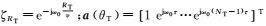
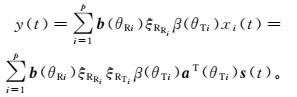 (4)
(4) 式中: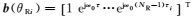
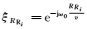
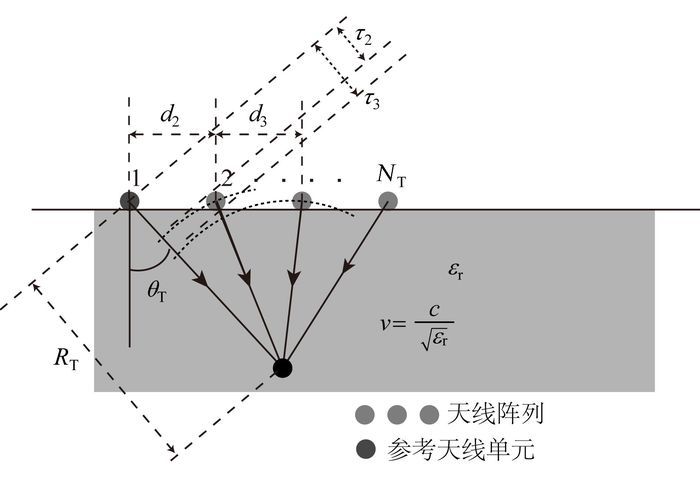
对于更广泛的非均匀天线阵列的情况,系统信号模型的区别在于阵列导向矢量的不同,a(θT)和b(θR)变成具通用性的形式a(θT)和b(θR),各参数示意见图 3。
|
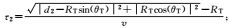 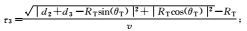 c.真空中的光速;εr.相对介电常数。
图 3 广义发射天线阵列
Figure 3 Generalized transmitting antenna array c.真空中的光速;εr.相对介电常数。
图 3 广义发射天线阵列
Figure 3 Generalized transmitting antenna array
|
|
|
 (5)
(5) 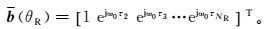 (6)
(6) 式中,τm(m=1, 2, …, NR)为第m个天线单元与参考天线的相对时移。
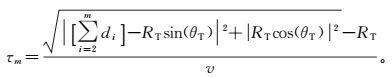 (7)
(7) 可见,对于非均匀连续阵列,阵列信号的方向矢量需由阵列单元分布参数di、目标相对参考天线的到达角和目标距离RT共同决定。在目标DOA估计中除了对DOA进行扫描估计之外,还需考虑目标距离参数RT。
2 目标成像方法本文目标成像方法的成像过程可分为3个步骤。
第一步,从阵列信号中通过匹配滤波方法解调出发射的基带信号,并估计出阵列相对于目标的距离延时τ。
第二步,采用基于波束形成器的DOA估计法,估计出阵列所在测点位置处的目标响应信号DOA;并同时估计出目标响应的幅度与相位(amplitude and phase, AP)。
第三步,根据τ、DOA、AP对成像空间进行扫描,对目标进行成像。其中,目标成像的信息来自两个方面:一是由正交性获得的各发射天线单元的幅度信息,二是窄带载波信号在阵列上表现出的相位信息。
2.1 目标DOA估计方法阵列信号模型为
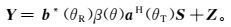 (8)
(8) 式中:Y∈NR×N为接收信号矩阵;β(θ)为在方向θ上的目标反射信号复幅度,它与在方向θ上目标的雷达散射截面成正比;S=[s1 s2 … sN]为发射的基带信号;Z∈NR×N为剩余项,它包含了噪声及干扰[15];*表示共轭;H表示共轭的转置。成像的问题在于如何从接收信号Y中估计出所有θ角度上的目标反射信号幅度β(θ),从而可以形成一个空间谱。
我们建立的信号模型忽略了目标信号到达延时(time of arrival, TOA,即τ),式(8) 也很容易扩展到目标回波信号τ未知的情况。采用现有方法同时估计出τ和β(θ)之后,即可形成2D雷达检测图像。我们提出的MIMO-GPR逆向投影成像方法只从阵列信号中估计出DOA,目标位置或距离参数不直接从TOA中获取,而是由多个估计DOA的几何关系来确定,从样就避开了目标反射信号时延和速度估计不精确的问题。
自适应波束形成的基本思想是使波束最大值指向目标方向的同时,尽可能地抑制干扰和噪声功率;这等价于在保证信号功率为一定值的条件下,使波束形成输出的总功率最小[16]。
在数学上可以将自适应波束形成一般框架描述为一个带约束的二次优化问题,即
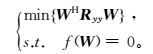 (9)
(9) 式中:W∈NR×1是空域滤波器的权向量,用于在压制噪声和干扰的同时保持信号不失真;矩阵Ryy是天线单元观测信号采样值(时间样点数为Ns)的协方差矩阵。
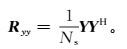 (10)
(10) 我们分别采用LS估计、Capon估计及APES的最优化波束形成算法来实现DOA的估计。
2.2 3种DOA估计对比建立MIMO雷达探测仿真模型,分析不同参数条件下的DOA估计性能。背景介质εr=9,载波频率f0=0.1 GHz,则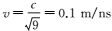
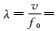

|
| 图 4 单目标体模型 Figure 4 Single target model |
|
|
阵列1号参考天线单元在(0, 0) 处,则点目标相对阵列的DOA为45°。图 5给出了SNR为0 dB时单目标体模型3种DOA估计在角度分辨率上的对比结果。从图 5中可以看出,3种方法都具有相同的幅度估计精度,然而在角度分辨率方面,它们具有较大的差异:Capon估计具有较高的DOA分辨率,其次是APES和LS估计。

|
| 图 5 单目标体模型3种DOA估计β(θ)比较 Figure 5 Comparison for β(θ) in three DOA methods for single target |
|
|
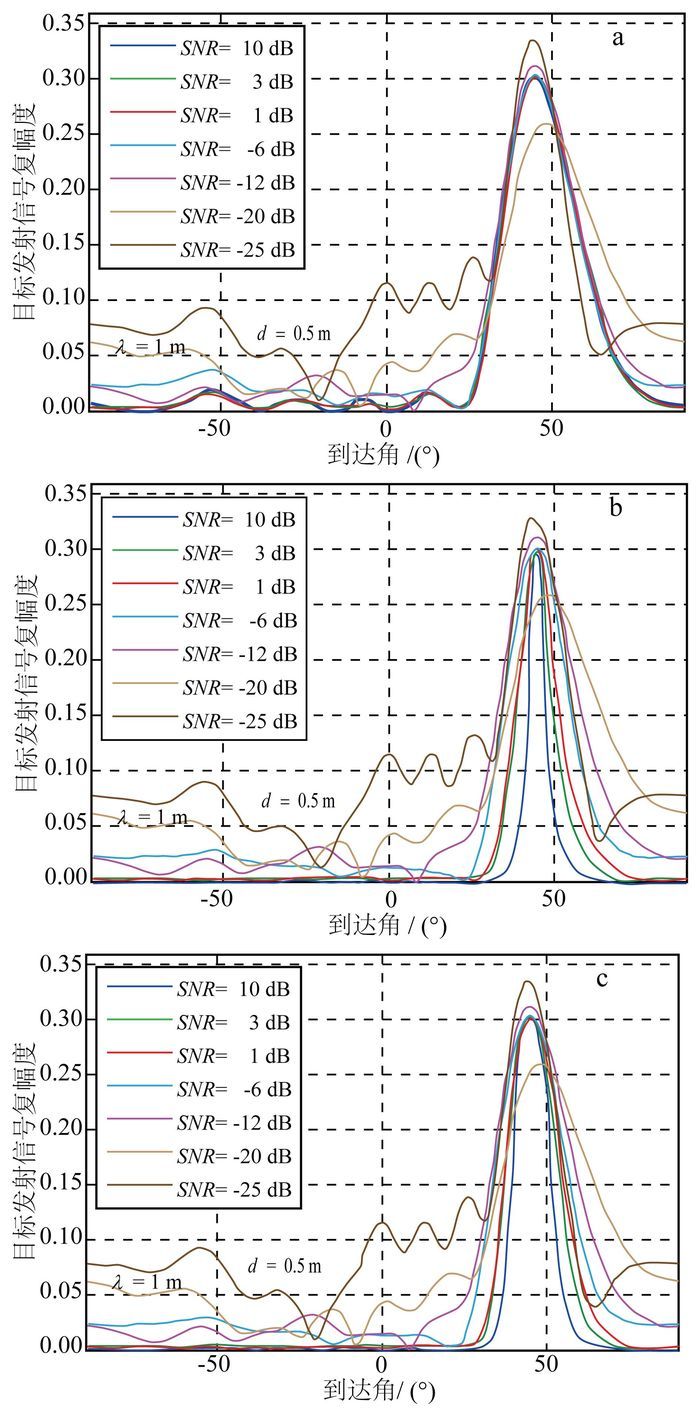
图 6给出了SNR为-25~10 dB时3种DOA估计的结果对比。可以看出,在低信噪比的情况下,3种DOA估计结果基本相同:在信噪比低于-20 dB的情况下,3种估计方法都出现比较大的旁瓣,这会造成假目标的出现,或是削弱目标位置处的成像能量。在目标方向上:LS估计的估计精度几乎与信噪比无关;而Capon估计虽然在高信噪比的情况下对目标DOA的估计具有较高的精度,但是其角度估计精度随信噪比的降低而降低;APES的估计性能介于LS估计与Capon估计之间。
|
| a.LS估计;b.Capon估计;c.APES。 图 6 单目标体模型3种DOA估计β(θ)与SNR的关系 Figure 6 Relationship between β(θ) and SNR in three DOA methods for single target |
|
|
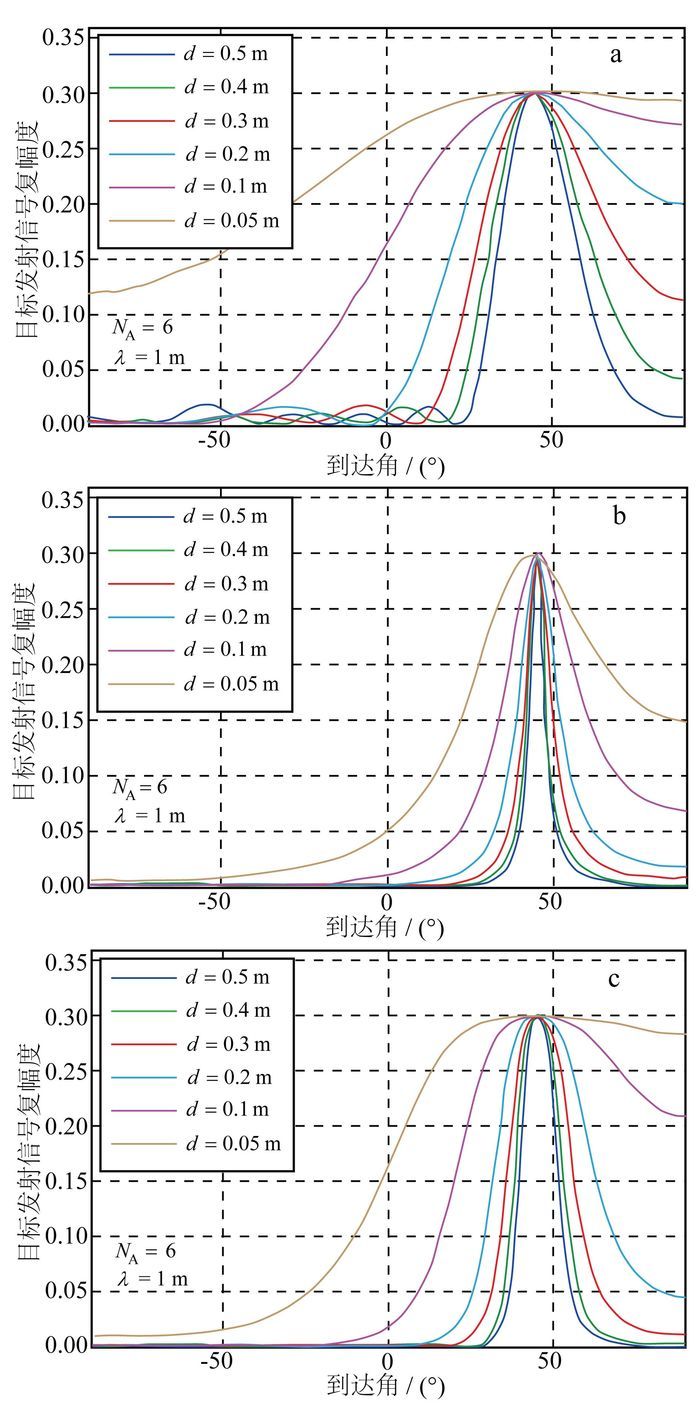
图 7给出了不同天线单元距条件下3种DOA估计的结果对比。阵列天线单元数NA=6,天线单元间距d=λ/2~λ/10。对比图 7可以明显看出,Capon估计在小天线间距的情况下仍有比较高的估计精度和稳定性。随着天线间距的减小,LS估计精度迅速降低,与Capon估计和APES相比,存在比较大的旁瓣振荡,在小天线间距情况下几乎无法估计出目标的DOA。而Capon估计仍有比较高的角度分辨率。因此,Capon估计和APES的DOA估计都具有比较高的稳定性。
|
| a.LS估计;b.Capon估计;c.APES。 图 7 单目标体模型3种DOA估计β(θ)与d的关系 Figure 7 Relationship between β(θ) and d in three DOA methods for single target |
|
|
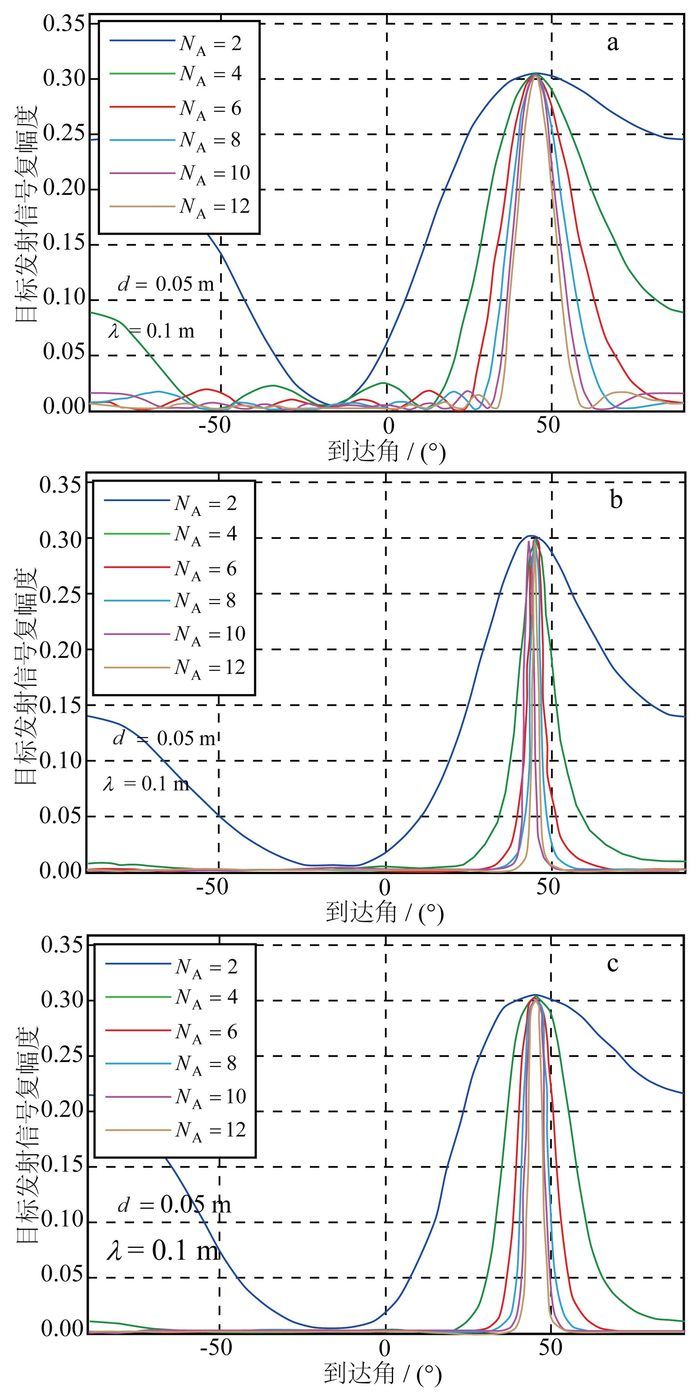
图 8给出了d不变、NA改变时,3种DOA估计的结果对比。从图 8可以看出:3种DOA估计方法在NA为2的情况下都无法很好地估计出目标DOA,目标方向无法分辨;但是当NA≥4时,3种方法都能比较地给出DOA估计;APES与Capon估计具有相近的DOA估计精度,LS估计次之。
|
| a.LS估计;b.Capon估计;c.APES。 图 8 单目标体模型3种DOA估计β(θ)与NA的关系 Figure 8 Relationship between β(θ) and NA in three DOA methods for single target |
|
|
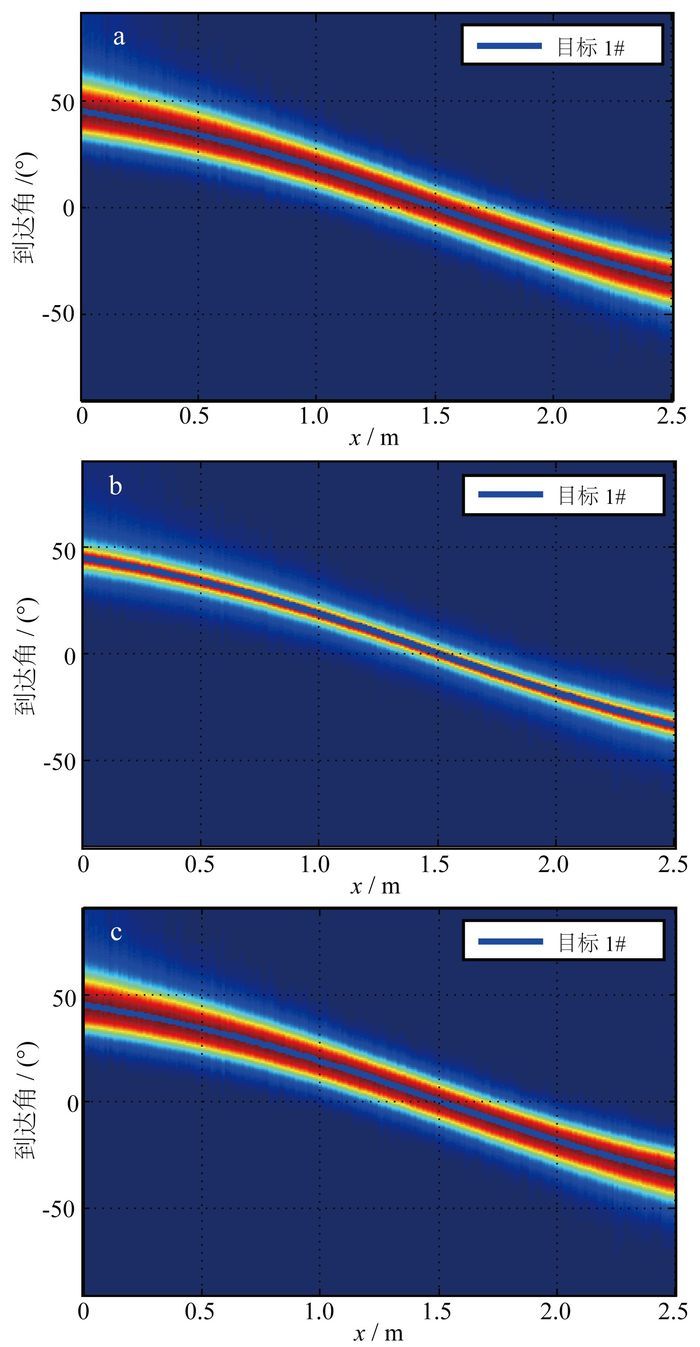
另外,我们采用类似于常规脉冲探地雷达的剖面观测方式,雷达天线阵列沿水平方向进行多次测量,并估计目标DOA值。图 9给出了这种观测方式下单目标体模型的连续DOA估计结果。从图 9可以看出:LS估计和APES在目标DOA为小角度时,估计精度比较低,在大角度时能获得较高的分辨率;Capon估计在整个目标DOA范围内都能获得比较高的估计精度。
|
| a.LS估计;b.Capon估计;c.APES。 图 9 单目标体模型测线不同位置的DOA估计值 Figure 9 DOA in different positions of the measuring line for single target |
|
|
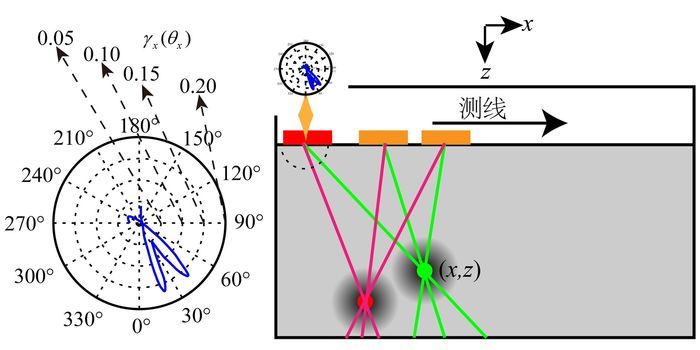
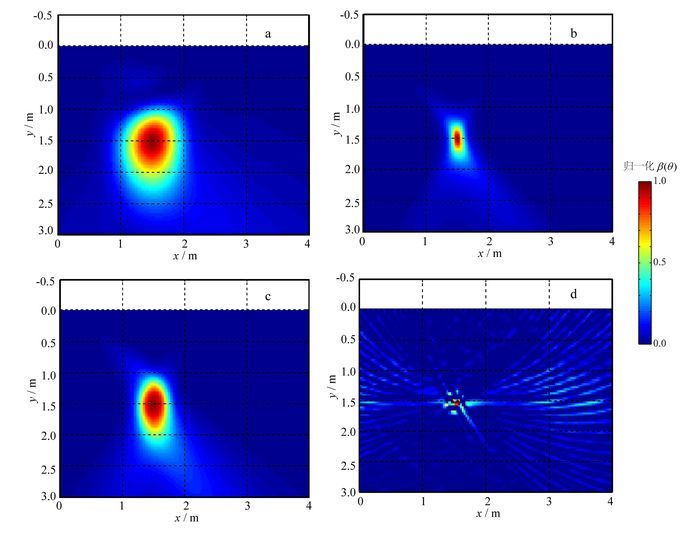
基于DOA估计的逆向投影目标成像方法原理如图 10所示。在二维模型假设条件下,设观测阵列沿地表y=0测量、成像点为(x, z),则在测线x上成像点对应的目标DOA信号幅度系数为γx(θx),DOA变化范围为[-90°, 90°]。其中,目标点方位角θx=arctan(x2+z2)。成像点(x, z)的成像值P(x, z)可通过叠加阵列所有观测位置x的DOA信号幅度系数得到:
|
| 图 10 基于DOA估计的逆向投影目标成像法原理示意图 Figure 10 IDIM Principle schematic diagram based on DOA estimation |
|
|
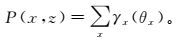 (11)
(11) 可见,P(x, z)是阵列观测空间位置和θx的函数。该成像方法利用了阵列空间观测位置的多样性和由DOA估计出的信号幅度系数,而不利用与速度关系密切的时间延时参数,从而避开了速度估计不精确的问题。
2.3.1 单目标体成像单目标体模型如图 4所示。收发共用均匀线性天线阵列,NT=NR=6,d=2.5 cm,天线阵列总长LAnt=5 d=12.5 cm。阵列移动范围为x=0~2.5 m,共均匀地采集了50个测点数据。
图 11a、b、c分别为基于LS估计、Capon估计和APES的DOA估计成像结果,可见Capon估计相对于其他两种方法明显具有较高的成像分辨率。图 11d为采用传统逆时偏移算法(RTM)对相同模型仿真数据进行成像的结果。对于单一的点目标探测,RTM具有很高的目标分辨率,能给出更为精确的目标坐标位置和深度信息;但在整个偏移剖上也出现了许多条纹状的偏移误差,这使得成像结果显得略为混乱。
|
| a.LS估计;b.Capon估计;c.APES;d.RTM。 图 11 单目标体不同方法反演成像结果图 Figure 11 IDIM results of different method for single target |
|
|
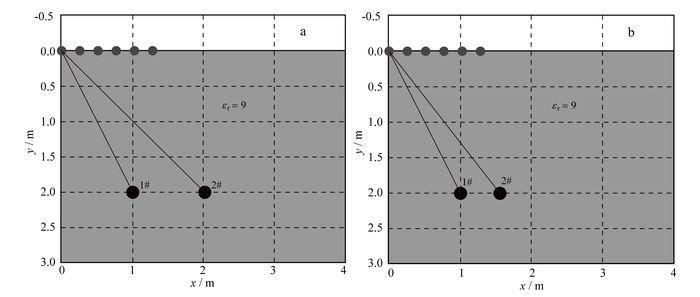
多目标体模型如图 12所示,系统观测参数与单目标体模型相同。模型中两目标体沿水平方向放置,但间距不同,模型一的目标间距为1 m,模型二的目标间距为0.5 m。图 13—图 16为目标成像结果。
|
| a.模型一;b.模型二。 图 12 水平间距不同的两目标体模型 Figure 12 Two-target model equidistant to the array initial position |
|
|

|
| a.模型一;b.模型二。 图 13 LS估计成像结果 Figure 13 LS IDIM imaging results |
|
|
|
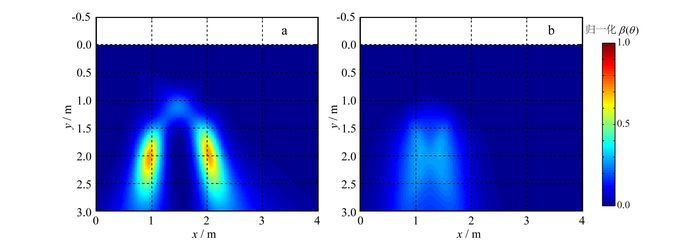
| a.模型一;b.模型二。 图 14 Capon估计成像结果 Figure 14 Capon IDIM imaging results |
|
|
|
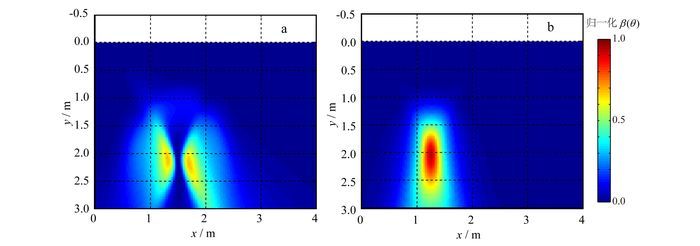
| a.模型一;b.模型二。 图 15 APES成像结果 Figure 15 APES IDIM imaging results |
|
|

|
| a.模型一;b.模型二。 图 16 RTM成像结果 Figure 16 Reverse time migration imaging results |
|
|
图 13、14、图 15分别为两目标体模型LS估计、Capon估计和APES的DOA估计方法成像结果。对于模型一,3种DOA估计方法都能获得比较好的成像结果。LS估计对两个目标的成像精度相对其他两种方法较低,目标范围较大;LS估计及APES在位置估计上存在较大的偏差,这是由于其DOA估计的角度分辨率不足引起的。具体而言,模型中两个目标都位于测线范围正下方,阵列可观测目标角度包含了目标地表一侧的正负DOA角度值,因此目标成像结果的水平分辨率较高;而由于目标的测线张角较小,成像结果的垂向分辨率则较低。LS估计使两目标沿水平方向间距增大,是目标对阵列观测位置张角不同引起的:目标1#阵列观测位置主要集中在负角度范围,则目标成像沿水平向左拉伸上,即成像向左侧偏移;与之相反,目标2#阵列观测位置的张角主要集中在正角度范围,则目标成像沿水平向右拉伸,即成像向右侧偏移,最终使两目标间距增大。
对于模型二,LS估计及APES成像方法精度严重降低,已经无法反映出目标体数目;Capon估计虽然对目标反射幅度估计降低了许多,但是其对目标位置的估计仍比较好。
图 16为两目标体模型RTM成像结果。逆时偏移结果相对于基于DOA估计的逆向成像方法具有较高的目标分辨能力,目标反演位置比较精确;但其散射条件也更为复杂,并分布于整个反演成像剖面。基于DOA估计的逆向成像算法虽然在两目标间距比较小的情况下都无法正确估计出目标数和目标位置,但成像剖面显得比较平滑,易于确定目标的存在大致区域;而RTM结果中误差条纹复杂多样,空间分布广、复杂的偏移衍射条纹可能会在目标个数多、分布空间不明确时造成目标误判问题。
3 结论1) 本文分析了LS估计、Capon估计及APES 3种基于自适应波束形成的DOA估计方法的精度及目标成像特征,提出了基于DOA估计的阵列探地雷达目标成像方法,并与常规逆时偏移成像算法进行了对比分析。
2) 在3种DOA估计方法中,Capon估计具有较高的DOA估计分辨率。在目标方向上,LS估计的精度几乎与信噪比无关,APES的性能介于LS估计与Capon估计之间;Capon估计在小天线距下仍有较高的估计精度和稳定性。
3) 基于DOA估计的逆向投影目标成像方法能比较好地对点目标进行成像,它需要在不同的空间位置进行数次采集,并联合阵列信号处理估计出的DOA对目标进行成像。成像方法从成像模型空间从发,扫描成像空间中各成像点,对各测点估计出的DOA幅度值在成像点位置进行积分求和即可同时进行目标位置及幅度的定位,从而获得目标更精确的位置参数,提高了目标检测的精度。虽然基于DOA估计的逆向投影目标成像方法在目标偏移成像分辨率和精度方面略差于逆时偏移算法,但是该方向成像算法实现简单、高效,可以广泛应用于地下孤石、地雷、地下管线等独立浅层地下埋设物方面的探测。
| [1] | Jabbarian-Jahromi M, Kahaei M H. Two-Dimensional SLIM with Application to Pulse Doppler MIMO Radars[J]. Eurasip Journal on Advances in Signal Processing, 2015(1): 1-12. |
| [2] |
王天云. 分布式雷达稀疏成像技术研究[D]. 合肥: 中国科学技术大学, 2015: 3-25
Wang Tianyun. Research on Distributed Radar Sparse Imaging Technologies [D]. Hefei: University of Science and Technology of China, 2015: 3-25. |
| [3] | 习建军, 曾昭发, 黄玲, 等. 阵列式探地雷达信号极化场特征[J]. 吉林大学学报(地球科学版), 2017, 47(2): 633-644. |
| [4] | Tan X, Roberts W, Li J, et al. Sparse Learning via Iterative Minimization with Application to MIMO Radar Imaging[J]. Signal Processing, 2014, 59(3): 1088-1101. |
| [5] | Xu L Z, Li J, Stoica P. Radar Imaging via Adaptive MIMO Techniques[C]//The 14th European Signal Processing Conference. [S. l.]: IET, 2006:1-5. |
| [6] | Tabrikian J. Barankin Bounds for Target Localization by MIMO Radars[C]//Sensor Array and Multichannel Processing. [S. l.]: IEEE, 2006:278-281. |
| [7] |
王鞠庭, 江胜利. 复合高斯杂波中MIMO雷达DOA估计的克拉美-罗下限[J].
电子与信息学报, 2009, 31(4): 786-789.
Wang Juting, Jiang Shengli. Cramer-Rao Bounds of DOA Estimation for MIMO Radars in Compound -Gaussian Clutter[J]. Journal of Electronics & Information Technology, 2009, 31(4): 786-789. |
| [8] |
夏威, 何子述. APES算法在MIMO雷达参数估计中的稳健性研究[J].
电子学报, 2008, 36(9): 1804-1809.
Xia Wei, He Zishu. On the Robustness of the APES Algorithm in the Parameter Estimation of MIMO Radars[J]. Acta Electronica Sinica, 2008, 36(9): 1804-1809. |
| [9] |
韩兴斌, 胡卫东, 郁文贤, 等. 分布式多通道雷达成像技术[J].
电子与信息学报, 2007, 29(10): 2354-2358.
Han Xingbin, Hu Weidong, Yu Wenxian, et al. An Imaging Technique Based on Distributed Multi-Channel Radars[J]. Journal of Electronics & Information Technology, 2007, 29(10): 2354-2358. |
| [10] | Li N, Cui G, Kong L, et al. MIMO RadarMoving Target Detection Against Compound-Gaussian Clutter[J]. Circuits Systems & Signal Processing, 2014, 33(6): 1-21. |
| [11] | Ma X Y, Wang D W, Su Y. High-Resolution Imaging Using a Narrowband MIMO Radar System[C]//The 9th Internation Conference on Signal Processing. Beijing: IET, 2008:2263-2267. |
| [12] | Wang H J, Su Y. Narrowband MIMO Radar Imaging with Two Orthogonal Linear T/R arrays[C]//The 9th Internation Conference on Signal Processing. Beijing: IET, 2008:2513-2516. |
| [13] | Zeng Zhaofa, Li Jing, Huang Ling, et al. Improving Target Detection Accuracy Based on Multipolarization MIMO GPR[J]. Geosciences and Remote Sensing, 2015, 53(1): 15-24. DOI:10.1109/TGRS.2014.2312937 |
| [14] | Zhao Y N, Li F C, Zhang T, et al. Computational Design of Optimal Waveforms for MIMO Radar via Multi-Dimensional Iterative Spectral Approximation[J]. Multidimensional Systems & Signal Processing, 2016, 27(1): 1-18. |
| [15] | Fuhnrmann D R, Antonio G S. Transmit Beamfo-nning for MIMO Radar Systems Using Partial Signal Correlation[C]//Conference Record of The 38th Asilmar Conference on Signals Systems and Computers. [S. l.]: IET, 2014:295-299. |
| [16] | Liu X, Sun C, Zhuo J, et al. High-Resolution Swath Bathymetry Using MIMO Sonar System[J]. Journal of Systems Engineering and Electronics, 2014, 25(5): 761-768. |



