0 引言
瞬变电磁法(transient electromagnetic,TEM)是一种广泛应用于水文地质和工程勘探等领域的时间域电磁勘探方法。在野外勘测中人们发现,TEM响应有时会在电流关断后出现负感应电动势并出现符号反转现象。符号反转通常出现在曲线中期或晚期,但在曲线早期也可能被探测到[1-2]。这种现象无法通过实电阻率解释,被认为可能是由磁效应、层间反射或复电阻率效应造成的[3-4]。很多学者对此进行了研究,其中:Cole-Cole模型通常被用来模拟大地的激发极化效应[5-8];Hohmann等[9]给出了激发极化效应影响TEM响应的基本近似理论;殷长春等[10]、王隆平等[11]、徐凯军等[12]通过正演计算分析了不同复电阻率参数的影响规律。
在TEM反演方面,Zhdanov等[13]利用浮动薄板解释法,通过视纵向电导曲线特征值划分地层进行近似解释;Nabighian等[14]利用烟圈理论解释法研究了TEM响应随时间的变化规律;翁爱华[15]将Occam方法应用到了TEM反演中,并得到了较为准确的结果。
以上方法均采用实电阻率反演,在考虑激发极化效应的TEM反演方面,目前的研究并不多,且很少应用最优化算法[16]。EI-Kaliouby等[17]通过分析响应的负值特征确定均匀极化半空间的Cole-Cole模型参数,并给出了计算最大负值的近似公式;Kozhevnikov等[18]采用单独反演与联合反演法对二层模型进行了复电阻率反演,证明联合反演可以在缺少先验信息的情况下分辨极化地层。
本文首先实现考虑激发极化效应的瞬变电磁一维正演,并在此基础上,采用Occam方法研究层状极化模型中的复电阻率反演,以缓解多参数引起的欠定性[19-20]。最后,通过典型理论层状极化模型试算验证算法的合理性和稳定性。该算法可以解决传统实电阻率反演无法解释瞬变电磁中负值响应的问题,具有较强的理论和实际应用意义。
1 算法基本原理 1.1 正演计算在频率域中,瞬变电磁中心回线产生的总磁场可以表示为水平电偶极子产生的垂直磁场积分累加和[21],即
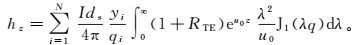 (1)
(1) 式中:hz为x方向水平电偶极子产生的垂直磁场;N为线源剖分的水平电偶极子总数;yi为第i个水平电偶极子的y坐标值;qi为第i个电偶极子的径向距离(q2=x2+y2);I为电流;ds为电偶极子长度;RTE为反射系数;z为场点的高度;λ=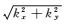
用Cole-Cole复电阻率模型(式(2))替换频率域中的实电阻率,再利用正弦变换数值滤波法完成频率域到时间域的转换,最终得到瞬变电磁场的时间域响应fsin(t)。
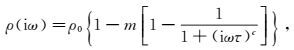 (2)
(2) 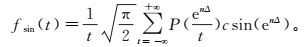 (3)
(3) 式中:ω为角频率;ρ0为零频电阻率;m为充电率;τ为时间常数;c为频率相关系数;t为时间;P为频率域函数;n为滤波系数的数目,n值越大,计算的精度越高、速度越慢[22];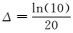
图 1为对正演结果的验证。实电阻率正演结果验证采用圆形回线作为发射源,半径为50 m,置于电阻率为100 Ω·m的均匀大地上,供电电流为1 A。在t=0时切断电流,并观测垂直磁场对时间的导数。圆形回线中心垂直磁场对时间的导数随时间的变化曲线由晚延时段解析解公式算出:
|
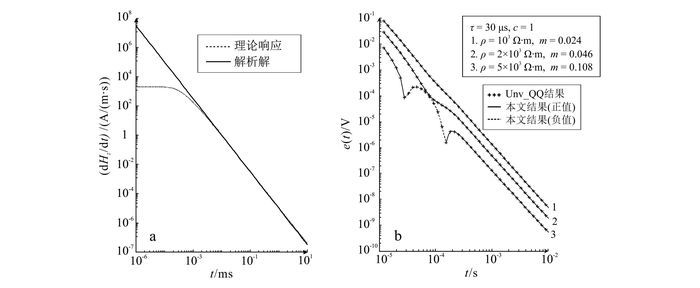
| a.实电阻率验证;b.复电阻率验证。 图 1 正演计算验证图 Figure 1 Transient electromagnetic (TEM) forward modeling validation |
|
|
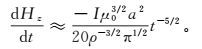 (4)
(4) 式中:Hz为圆形回线中心垂直磁场;ρ为电阻率;a为圆回线半径。由圆形回线等效面积换算的中心回线边长为88.62 m。由图 1a可以看出,晚延时段(0.01 ms以后)理论计算值与解析解重合,验证了实电阻率正演计算的可靠性。
复电阻率正演结果验证采用100 m×100 m的重叠回线作为发射源,在均匀极化半空间中观测感应电动势e(t)。由于感应电动势与垂直磁场对时间的导数成正比,所以后文中均采用感应电动势作为正演响应。由图 1b可以看出,复电阻率正演计算结果与Kozhevnikov等[16]编写的Unv_QQ程序结果一致,验证了复电阻率正演计算的可靠性。
1.2 反演计算在地球物理反演问题中,关于观测数据和模型参数的非线性方程可以表示为
 (5)
(5) 式中:d=(d1, ..., dN)为观测数据矢量,由N个时间道的观测数据组成;F为理论正演函数;m为模型参数,代表 4种复电阻率参数,每个复电阻率参数的数量为M个,共有4M个参数;ε为方差为σ2的噪声。
反演问题可以通过对目标函数的最优化来解决[19]。定义观测数据与模型参数正演数据之间的数据拟合差为
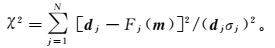 (6)
(6) 式中:Fj为与dj相对应的第j个正演函数值;σj为第j个数据的标准差。式(6) 通过对dj进行归一化,可以保证早期和晚期的观测数据拥有一致的权值。将式(6) 表示为矩阵形式,为
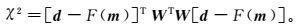 (7)
(7) 其中,权值矩阵W为
 (8)
(8) 式中,diag代表对角矩阵。
反演过程就是最小化χ2的过程。
由于观测数据有限,仅靠拟合数据进行反演往往会在升高分辨率的同时降低可靠性,这时就需要加入Occam平滑模型约束R(也称为粗糙度矩阵)来控制分辨率,突出主要异常。模型粗糙度也可以写为
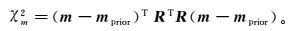 (9)
(9) 式中:mprior为先验模型参数;R为N×N阶模型约束矩阵。
 (10)
(10) 拟合差项和粗糙度项之间的权重用拉格朗日因子来平衡。综上,反演目标函数可以定义为
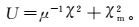 (11)
(11) 式中,μ为拉格朗日因子,是模型光滑和数据拟合的折衷参数。
F[m]是m的非线性函数,所以目标函数也是非线性的。为了将其线性化,在模型参数的上一次迭代值m1附近进行Taylor级数展开并略去二阶以上高阶项,得
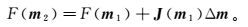 (12)
(12) 式中: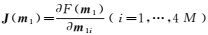
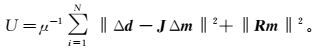 (13)
(13) 式中,Δd=d-F(m1)。对Δm求导并令其等于零,整理得
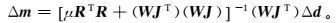 (14)
(14) 但事实上,式(14) 中的矩阵大多数情况下是病态的,所以直接求逆并不稳定。于是Marquardt[23]提出了一种修正方法,即让每次模型改变量是被阻尼的。其形式为
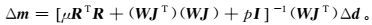 (15)
(15) 式中:I为单位矩阵;p是用来控制步长的阻尼因子,其值随拟合差变化而变化。得到模型修正量Δm后,由式(16) 更新模型,继续进行下一次迭代。
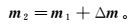 (16)
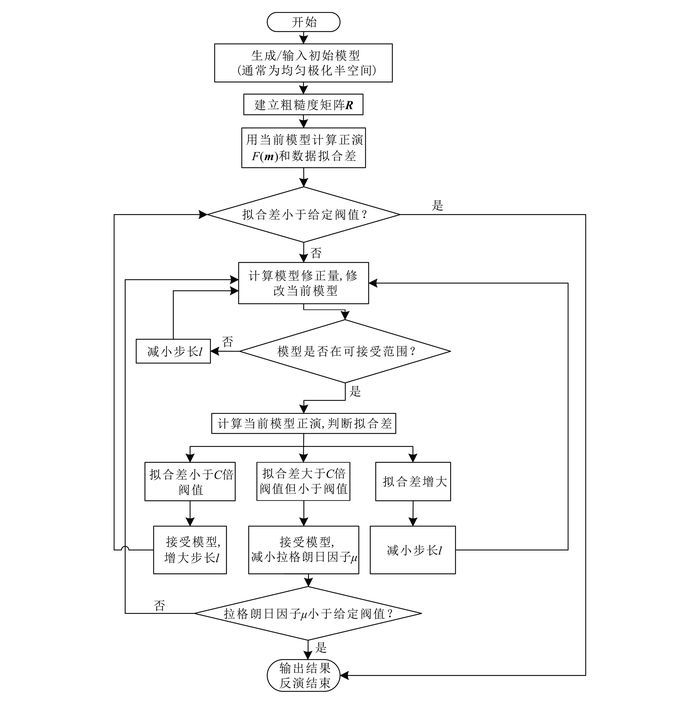
(16) 由式(15) 以及图 2可以看出,迭代过程是通过修改阻尼因子p和拉格朗日因子μ来控制的。p控制收敛程度:当模型改变导致拟合差增加时,增大p以减小步长,重新搜索目标函数下降方向;当拟合差减小时,减小p以增大步长,使目标函数沿下降方向修改模型,继续下一次迭代。μ控制拟合数据与模型平滑之间的平衡。每次迭代的更新模型mn+1为μ的函数,通过线性搜索可以找到最佳μ值,从而使拟合差达到最小[19]。但一维搜索需要多次正演计算,过程十分缓慢,所以此处采用μ值在一定步长下逐次递减的简单求取方法,即在反演开始阶段给定初始μ0及步长l>1,较大的μ0值可以保证反演不受初始模型的影响。当拟合差小于前一次迭代拟合差的C倍阀值时(本文中取C=0.8),令当前第k次迭代的拉格朗日因子μk变为μk-1/l。随着迭代进行,μ值逐渐减小,目标函数中拟合差项的权值逐渐增大,最终使其满足给定的误差阀值。
|
| 图 2 算法流程图 Figure 2 Inversion flow chart |
|
|
下面分别通过典型H型低阻高极化地层和K型高阻低极化地层模型来检测复电阻率法的反演能力,并与实电阻率反演作为对比。算例均采用1匝400 m×400 m的回线作为发射源,并用1匝面积为200 m2的回线接收;回线均水平置于地面,接收回线位于发射回线中心;发射电流为17 A,数据采集时间窗口共30道。初始阻尼因子和拉格朗日因子均为100,要求迭代终止拟合差阀值为7.0×10-6,最多迭代次数为50次。复电阻率和实电阻率初始模型均为对数等间隔厚度的15层均匀半空间。对于H型模型:初始地层参数ρ0=100 Ω·m,m=0.3,τ=0.2 s,c=0.3;实电阻率初始地层参数ρ=100 Ω·m。对于K型模型:初始地层参数ρ0=70 Ω·m,m=0.3,τ=0.4 s,c=0.3;实电阻率初始地层参数ρ=70 Ω·m。理论模型响应均加入了5%的随机噪声。
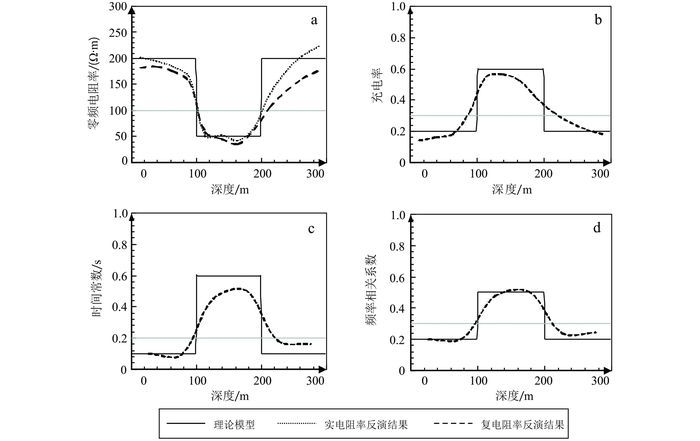
图 3为H型模型的反演结果,由于加入了平滑模型,所以反演结果没有突跳现象。从零频电阻率的反演结果(图 3a)可以看出,实电阻率比复电阻率的反演值要略高一些。这是由于实电阻率没有考虑与感应电流方向相反的感应激发极化电流,所以将瞬变响应中快速下降的部分误判为由高阻地层引起,从而导致其反演值高于复电阻率反演值。4种复电阻率参数在反演结束时均能得到较好的恢复,但在反演过程中,由于零频电阻率和充电率的灵敏度大于时间常数和频率相关系数的灵敏度,所以时间常数和频率相关系数需要比前两个参数更长的反演时间来恢复到接近真实值。
|
| 图 3 H型模型复电阻率反演结果 Figure 3 Inversion results of model H |
|
|
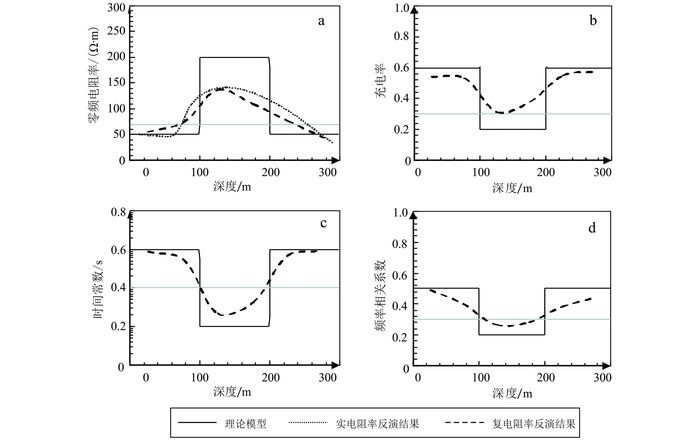
图 4为K型模型的反演结果。从零频电阻率的反演结果(图 4a)仍可以看出实电阻率反演结果比复电阻率略高。与H型模型对比发现,高阻极化层的反演效果不如低阻极化层,4种复电阻率参数虽然在变化趋势上与理论模型一致,但均没有恢复到真实值。而且,由于低阻围岩压制了激发极化效应,导致时间常数的灵敏度不如其他3个参数,但经过较多次数的迭代,时间常数仍可得到较好的恢复。
|
| 图 4 K型模型复电阻率反演结果 Figure 4 Inversion results of model K |
|
|
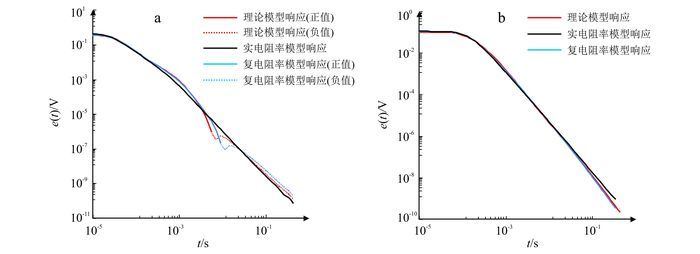
图 5为H型模型和K型模型的响应拟合曲线,响应值均由图 3和图 4中的理论复电阻率模型参数值计算得出。从图 5a中可以看出,由于高阻围岩中感应电流衰减速度很快,所以激发极化效果十分明显,并且在晚期响应中出现负值变号现象。复电阻率反演结果在早期拟合良好,同时也能拟合晚期响应的负值部分;实电阻率反演只能通过正值去拟合响应,对于晚期的负值特征则无法表现。K型模型由于存在低阻围岩,感应电流衰减比H型模型要慢,在晚期仍然占据主要作用且强度高于感应激发极化电流,所以在晚期没有出现负值;此时K型模型中的激发极化效应不明显,复电阻率反演和实电阻率反演的最终响应曲线在早期和中期均能很好地拟合观测数据,仅在晚期有细微的不同(图 5b)。
|
| 图 5 H型模型(a)和K型模型(b)的响应拟合曲线 Figure 5 Fitting curves of model H (a) and model K (b) |
|
|
H型模型和K型模型的反演拟合差以及迭代次数见表 1,反演均稳定收敛。
| 电阻率 | 模型 | 迭代次数 | 拟合差/10-6 |
| 复电阻率 | H型模型 | 17 | 1.830 504 |
| K型模型 | 22 | 5.507 210 | |
| 实电阻率 | H型模型 | 11 | 4.107 291 |
| K型模型 | 14 | 5.832 343 |
本文实现了瞬变电磁一维Occam复电阻率反演,通过对H型与K型极化模型的反演试算与结果分析,得到如下结论:
1) 高阻围岩中的感应电流衰减比低阻围岩中快,感应激发极化电流更容易占优势并出现负值变号现象。
2) 激发极化效应会造成瞬变响应的快速衰减,实电阻率反演由于没有考虑激发极化效应,导致其反演值升高。
3) 进行复电阻率反演不仅可以拟合观测得到的负值部分,而且还能很好地还原4种Cole-Cole模型参数;低阻高极化地层的反演效果强于高阻低极化地层;零频电阻率和充电率的灵敏度比时间常数和频率相关系数大,可以在反演中更快地恢复到接近真实值。
| [1] | Walker G G, Kawasaki K. Observation of Double Sign Reversals in Transient Electromagnetic Central Induction Soundings[J]. Geoexploration, 1988, 25(3): 245-254. DOI:10.1016/0016-7142(88)90019-1 |
| [2] | Descloitres M, Guérin R, Albouy Y, et al. Improve-ment in TDEM Sounding Interpretation in Presence of Induced Polarization: A Case Study in Resistive Rocks of the Fogo Volcano, Cape Verde Islands[J]. Journal of Applied Geophysics, 2000, 45(1): 1-18. DOI:10.1016/S0926-9851(00)00015-X |
| [3] | Weidelt P. Response Characteristics of Coincident Loop Transient Electromagnetic Systems[J]. Geophysics, 2012, 47(9): 1325-1330. |
| [4] | Spies B R. AField Occurrence of Sign Reversals with the Transient Electromagnetic Method[J]. Geophysical Prospecting, 1980, 28(4): 620-632. DOI:10.1111/gpr.1980.28.issue-4 |
| [5] | Pelton W H, Ward S H, Hallof P G, et al. Mineral Discrimination and Removal of Inductive Coupling with Multifrequency IP[J]. Geophysics, 1978, 43(3): 588-609. DOI:10.1190/1.1440839 |
| [6] | Flis M F, Newman G A, Hohmann G W. Induced-Polarization Effects in Time-Domain Electromagnetic Measurements[J]. Geophysics, 1989, 54(4): 514-523. DOI:10.1190/1.1442678 |
| [7] | Kaufman A A, Geoltrain S, Knoshaug R N. Influence of Induced Polarization in Inductive Methods[J]. Geoexploration, 1989, 26(2): 75-93. DOI:10.1016/0016-7142(89)90054-9 |
| [8] | Smith R S, West G F. Field Examples of Negative Coincident-Loop Transient Electromagnetic Responses Modeled with Polarizable Half-Planes[J]. Geophysics, 1989, 54(11): 1491-1498. DOI:10.1190/1.1442613 |
| [9] | Hohmann G W, Kintzinger P R, Van Voorhis G D, et al. Evaluation of the Measurement of Induced Electrical Polarization with an Inductive System[J]. Geophysics, 1970, 35(5): 901-915. DOI:10.1190/1.1440136 |
| [10] |
殷长春, 刘斌. 瞬变电磁法三维问题正演及激电效应特征研究[J].
地球物理学报, 1994, 37(增刊 1): 486-492.
Yin Changchun, Liu Bin. The Research on the 3D TDEM Modeling and IP Effect[J]. Acta Geophysica Sinica, 1994, 37(Sup. 1): 486-492. |
| [11] |
王隆平, 温佩琳. 论TEM法中的IP效应[J].
中南工业大学学报, 1998, 29(3): 209-211.
Wang Longping, Wen Peilin. IP Effects in TEM Response[J]. Journal of Central South University, 1998, 29(3): 209-211. |
| [12] |
徐凯军, 李桐林, 刘展. 激电效应对瞬变电磁影响特征研究[J].
物探化探计算技术, 2010, 32(6): 613-616.
Xu Kaijun, Li Tonglin, Liu Zhan. The Study of Induced Polarization Effect in Transient Electromagnetic Fields[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2010, 32(6): 613-616. |
| [13] | Zhdanov M S, Portniaguine O. Time-Domain Electro-magnetic Migration in the Solution of Inverse Problems[J]. Geophysical Journal International, 1997, 131(2): 293-309. DOI:10.1111/gji.1997.131.issue-2 |
| [14] | Nabighian M N, Macnae J C. Time Domain Electro-magnetic Prospecting Methods[J]. Electromagnetic Methods in Applied Geophysics, 1991, 2(Part A): 427-509. |
| [15] |
翁爱华. Occam反演及其在瞬变电磁测深中的应用[J].
地质与勘探, 2007, 43(5): 74-76.
Weng Aihua. Occam's Inversion and Its Application to Transient Electromagnetic Method[J]. Geology and Prospecting, 2007, 43(5): 74-76. |
| [16] | Kozhevnikov N O, Antonov E Y. Inversion of TEM Data Affected by Fast-Decaying Induced Polarization: Numerical Simulation Experiment with Homogeneous Half-Space[J]. Journal of Applied Geophysics, 2008, 66(1): 31-43. |
| [17] | El-Kaliouby H M, El-Diwany E A, Hussain S A, et al. Optimum Negative Response of a Coincident-Loop Electromagnetic System Above a Polarizable Half-Space[J]. Geophysics, 1997, 62(1): 75-79. DOI:10.1190/1.1444147 |
| [18] | Kozhevnikov N O, Antonov E Y. Inversion of IP-Affected TEM Responses of a Two-Layer Earth[J]. Russian Geology and Geophysics, 2010, 51(6): 708-718. DOI:10.1016/j.rgg.2010.05.011 |
| [19] | Constable S C, Parker R L, Constable C G. Occam's Inversion: A Practical Algorithm for Generating Smooth Models from Electromagnetic Sounding Data[J]. Geophysics, 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [20] |
朴英哲, 李桐林, 刘永亮. 在大地电磁二维Occam反演中求取拉格朗日乘子方法改进[J].
吉林大学学报(地球科学版), 2014, 44(2): 660-667.
Piao Yingzhe, Li Tonglin, Liu Yongliang. Improvement of Choosing Lagrange Multiplier on MT 2D Occam Inversion[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(2): 660-667. |
| [21] |
李建平, 李桐林, 张亚东. 层状介质任意形状回线源瞬变电磁场正反演[J].
物探与化探, 2012, 36(2): 256-259.
Li Jianping, Li Tonglin, Zhang Yadong. TEM Forward and Inversion of Arbitrary Shape Loop Source in Layered Media[J]. Geophysical & Geochemical Exploration, 2012, 36(2): 256-259. DOI:10.11720/wtyht.2012.2.21 |
| [22] |
王华军. 正余弦变换的数值滤波算法[J].
工程地球物理学报, 2004, 1(4): 329-335.
Wang Huajun. Digital Filter Algorithm of the Sine and Cosine Transform[J]. Chinese Journal of Engineering Geophysics, 2004, 1(4): 329-335. |
| [23] | Marquardt D W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441. DOI:10.1137/0111030 |



