2. 中国科学院电磁辐射与探测技术重点实验室, 北京 100190;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Electromagnetic Radiation and Sensing Technology, Chinese Academy of Sciences, Beijing 100190, China;
3. Chinese Academy of Sciences, Beijing 100049, China
0 引言
相较于基于大回线的时间域电磁法,基于磁偶极子模型的频率域电磁法具有不受关断时间影响、信噪比高等优点,可实现对浅地表的探测,目前已在地质普查、探矿、考古、城市地下管道探测等方面广泛应用。国内外市场上已有的频率域电磁系统主要有:应用于航空探测的法国CGG公司的DIGHEM系统[1-2]、RESOLVE系统[3]以及美国Geophex公司的GEM-2A系统[4]等,应用于地面探测的Geonics公司的EM31、EM34、EM38系统[5-7],Geophex公司的GEM-2、GEM-3、GEM-5系统[8-10]以及俄罗斯的NEMFIS系统[11]等。按照收发线圈摆放轴向的不同,会产生9种线圈架构;由于部分线圈架构具有几何对称性,通常只分析其中的6种[12];最常见的是垂直共轴(vertical coaxial,VCA)、垂直共面(vertical coplanar,VCP)、水平共面(horizontal coplanar,HCP)以及xz轴正交(perpendicular xz,PERxz)4种线圈架构[13]。
在频率域航空电磁法仪器的制作及探测过程中,不仅坡度较陡的地形对频率域航空电磁响应产生较大影响[14],收发线圈存在的安装误差、晃动以及材料形变等因素,使得收发线圈的位置及姿态角发生变化,也同样会产生较大的测量误差。而测量误差的存在使反演得到的层状大地电导率、磁化率以及各层厚度等参数存在误差,从而会影响到探测水深、海冰厚度时的精度[15-17]。因此,对收发线圈位置及姿态角变化引起的几何误差进行研究具有重要意义;另外,在指导仪器制作、系统校正以及野外实验的设计方面也具有重要价值[18-21]。为了便于分析几何误差,本文将几何误差根据误差来源的不同分为一次场误差及二次场误差两类。
在已有分析几何误差的文章中:Lin[22]着重分析比较了PERzx、PERzy线圈架构中接收线圈分别在yz轴向的位置变化、绕y轴旋转角变化引入的一次场误差,但并未对二次场误差进行分析;Yin等[19]分析校正了VCA、VCP与HCP 3种线圈架构收发线圈绕相同轴向旋转较大姿态角时引起的二次场误差,但并未分析收发线圈姿态角单独变化且变化较小时引起的二次场误差;王琦等[20]在分析校正姿态角变化引起二次场误差的同时,考虑了相应的收发距(收发线圈的水平间距)和高度变化,但未单独考虑位置变化引起的二次场误差;曲昕馨等[21]单独求取了由收发距和高度变化引起的位置误差,仅考虑了姿态角变化的情况,通用性不强。与Guillemoteau等[23]将入射波等效成TE波和TM波的方式进行姿态误差分析不同,本文通过引入一次场张量矩阵、位置误差矩阵以及姿态角旋转矩阵分别求取9种线圈架构收发线圈几何形变引起的一次场误差,通过引入二次场张量矩阵以及姿态角旋转矩阵求取VCA、VCP、HCP、PERxz 4种线圈架构由姿态角变化引起的二次场误差,而通过求取4种常用线圈架构下二次场对高度及收发距的微分得到了高度及收发距微小变化引起的二次场误差,从而为基于磁偶极子模型的频率域电磁法仪器制作、校正以及野外实验操作提供指导。
1 频率域电磁法几何误差正演模型在收发线圈理想放置的情况下,可精确地计算出接收线圈接收到的一次场值,或由理想放置的Bucking线圈测得[4, 8]。由于对Bucking线圈的几何误差分析与接收线圈类似,本文不再叙述Bucking线圈的影响。在收发线圈发生几何形变的情况下,接收线圈接收到的一次场会发生变化,从而产生一次场误差。而在系统实际测量时,该一次场误差则被视为二次场信号且仅引起了二次场同相分量的变化。由于频率域电磁法仪器的输出(包括同相分量Inphase与正交分量Quadrature)常以二次场与一次场的比值(以10-6为单位)表示[4, 8],为便于分析误差对信号的影响,本文通过求取一次场误差与理论一次场的比值,以及二次场误差与理论二次场的比值来定量地分析几何误差的变化特征及规律。
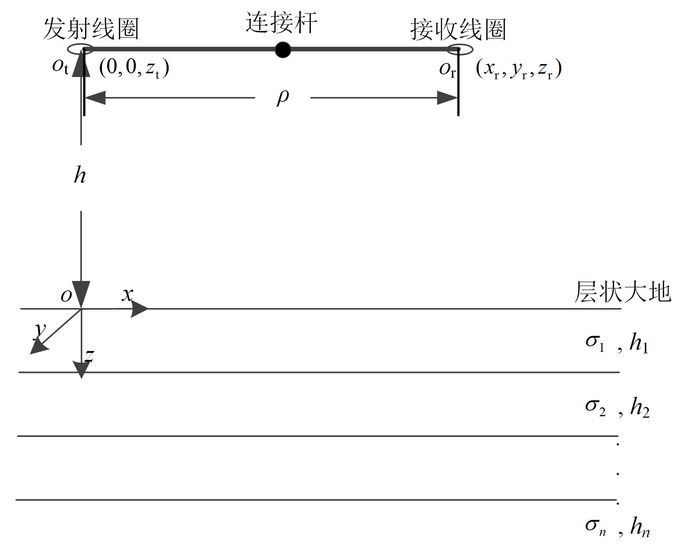
在直角坐标系下,以层状大地为研究模型(图 1),以发射线圈中心沿z轴方向的垂线与大地的交点为坐标原点O,收发线圈沿x轴向分布,可知发射线圈的坐标为(0, 0, -h),接收线圈的坐标为(xr, yr, zr)。
|
| 图 1 频率域电磁法仪器探测层状大地模型 Figure 1 Model of frequency domain electromagnetic instrument detecting layered earth |
|
|
当收发线圈的轴向分别取为x、y、z时,即为9种线圈架构。分别求取9种线圈架构接收线圈接收到的一次场,可得一次场张量矩阵[24]Hp:
 (1)
(1) 式中:Hpab分别对应9种线圈架构下的一次场值,b轴向发射、a轴向接收,a, b∈{x, y, z};rr=
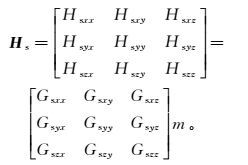 (2)
(2) 其中:
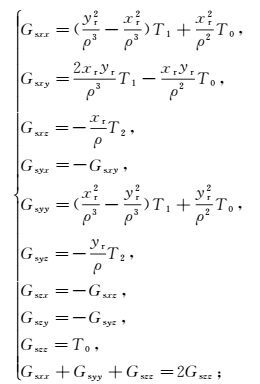 (3)
(3) 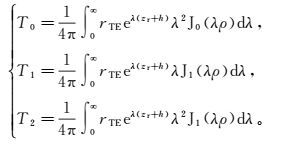 (4)
(4) 式中:Hsab分别对应于9种线圈架构下的二次场值;Gsab分别对应9种线圈架构下二次场的格林函数,b轴向发射、a轴向接收,a, b∈{x, y, z};ρ=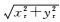
 (5)
(5) 式中:
由式(3) 可知,yr=0,此时Gsxy, Gsyz≡0,这与在实际探测时,运动方向取为x轴向方向相符。因此在考虑二次场误差时,主要分析Gsxx、Gsxz、Gsyy、Gszz4种常用的线圈架构。收发线圈姿态角与位置变化引起的几何误差求取公式中包含姿态角变化的正余弦函数、多个轴向的旋转姿态角变化与位置变化的乘积等参量,因此,在分析较小的姿态角变化(<0.01 rad)与位置变化(<0.01 m)时,可忽略一次场误差中的三次项及更高次项,可忽略二次场误差中的二次项及更高次项。
2 几何误差模型仿真文中在进行几何误差分析时,以Fugro公司的RESOLVE航空宽频带频率域电磁法仪器的技术参数[3]为仿真模型,收发距为7.9 m,采用直升机悬吊式搭载,飞行高度为30 m。为便于分析几何误差受系统发射频率f及大地电导率σ的影响,选用频率电导率乘积(即fσ)作为仿真变量[12]。选择待测大地电导率为0.02 S/m的均匀大地,此时频率电导率乘积的变化仅由发射频率的变化引起。
2.1 一次场误差 2.1.1 位置变化引入的一次场误差由式(1) 可知,位置变化引入的一次场误差是由收发线圈之间相对位置的变化引入的,因此可以只分析接收线圈位置的变化。设接收线圈位置发生变化后的坐标为(xr+Δxr, Δyr, zr+Δzr),带入式(1),将其进行多元函数的泰勒级数展开,在满足Δxr, Δyr, Δzr≪xr和xr=rr的条件下,可以忽略位置变化引起的三次及更高次项误差。另外,若Δxr、Δyr、Δzr存在一次项误差,由于一次项误差远大于二次项误差,则可以忽略相应的二次项误差。经过化简可得一次场位置误差为
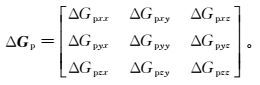 (6)
(6) 其中:
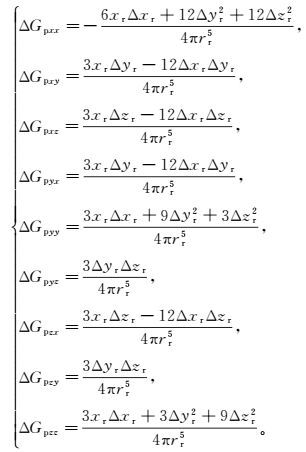 (7)
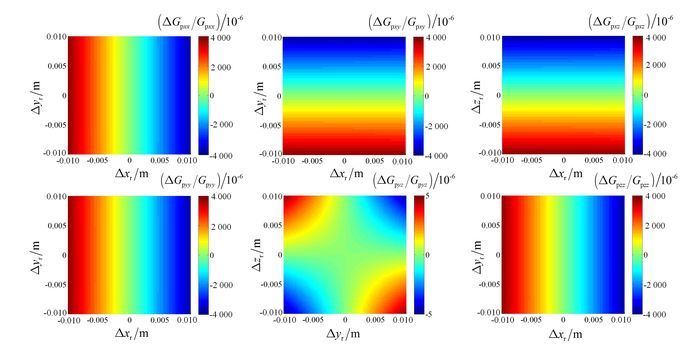
(7) 由式(6)、(7) 可知,位置变化引入的一次场误差满足对称性,即ΔGpxy=ΔGpyx,ΔGpxz=ΔGpzx,ΔGpyz=ΔGpzy。其中,ΔGpxy、ΔGpxz、ΔGpyz仅受其收发线圈轴向位置变化的影响,而ΔGpxx、ΔGpyy、ΔGpzz则与Δxr、Δyr、Δzr有关。已知ΔGpyy在Δyr与Δzr互换后成为ΔGpzz,且ΔGpxx中Δyr、Δzr本身具有对称性,则只需仿真ΔGpxx、ΔGpyy、ΔGpzz中Δxr、Δyr位置变化引入的一次场误差,结果如图 2所示。
|
| 图 2 6种线圈架构接收线圈位置变化引入的一次场误差 Figure 2 Primary field errors generated by position change of receiver coils of six coil configurations |
|
|
由图 2可知:Gpxx、Gpyy、Gpzz线圈架构的一次场误差与Δxr成线性关系;Gpxy(Gpyx)线圈架构的一次场误差与Δyr成线性关系;Gpxz(Gpzx)线圈架构的一次场误差与Δzr成线性关系;Gpxx线圈架构的一次场误差最大;仅有Gpyz(Gpzy)线圈架构的一次场误差中不包含位置变化的一次项误差。
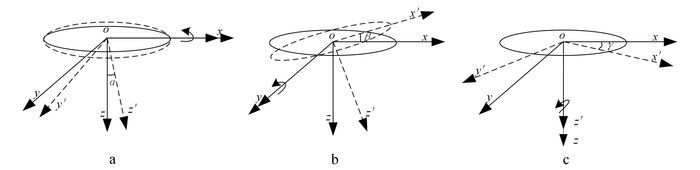
2.1.2 姿态角变化引入的一次场误差图 3所示为单个线圈姿态角的变化:线圈绕x轴旋转,产生摇摆角α;绕y轴旋转,产生俯仰角β;绕z轴旋转,产生偏航角γ。认为线圈姿态角未发生变化时处于惯性坐标系(x, y, z)下,而当线圈发生姿态角旋转后,处于线圈坐标系(x′, y′, z′)下。由惯性坐标系旋转为线圈坐标系,需要相应的姿态角旋转矩阵R:
|
| a.摇摆旋转;b.俯仰旋转;c.偏航旋转。 图 3 线圈姿态旋转示意图 Figure 3 Coil's attitude rotation schematic |
|
|
 (8)
(8) 其中:
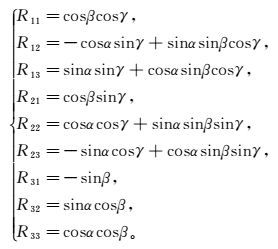 (9)
(9) 在忽略姿态角变化的三次及更高次项后,可将R化简为
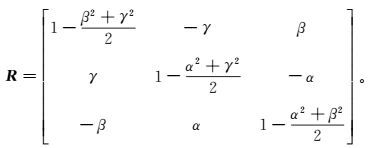 (10)
(10) 由于发射线圈与接收线圈旋转的角度可以不同,令Rt、Rr分别代表发射线圈、接收线圈的旋转矩阵,分别对应于旋转角αt、βt、γt, αr、βr、γr且均满足Rr-1=RrT, Rt-1=RtT,则
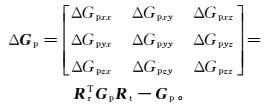 (11)
(11) 由式(7) 可知,Δxr、Δyr、Δzr不为零,仿真时取Δxr, Δyr, Δzr=0.001 m会引入位置变化的一次误差项及二次误差项,结合姿态角变化引起的误差,忽略三次及更高次项误差,式(11) 化简为
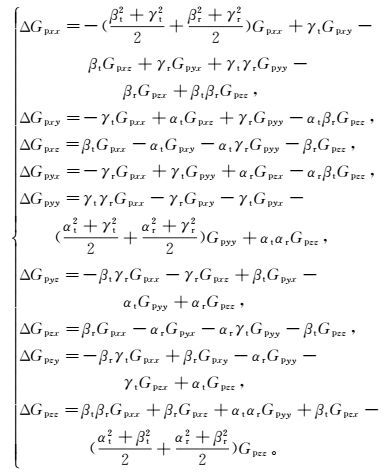 (12)
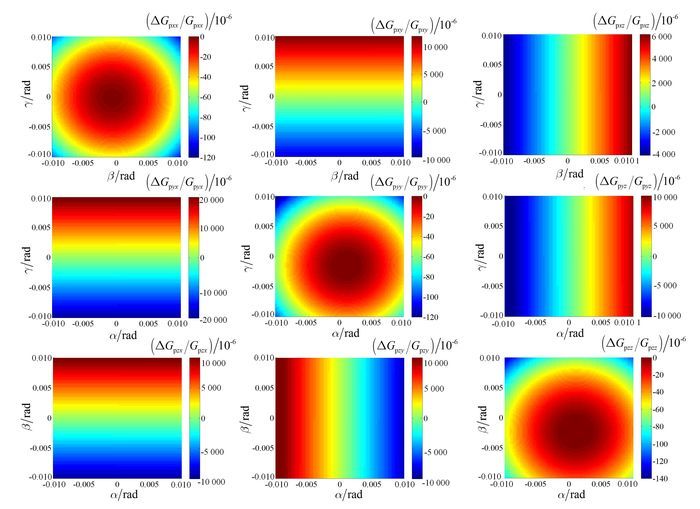
(12) 在满足Gpxy=Gpyx, Gpxz=Gpzx, Gpyz=Gpzy的情况下,根据收发线圈姿态角变化对误差作用的对称关系,只需分析接收线圈姿态角变化引入的一次场误差,此时取αt, βt, γt=0.001 rad,结果如图 4所示。
|
| 图 4 9种线圈架构接收线圈姿态角变化引入的一次场误差 Figure 4 Primary field errors generated by altitude change of receiver coil of nine coil configurations |
|
|
由图 4可知:Gpxy、Gpxz、Gpyx、Gpyz、Gpzx、Gpzy线圈架构中包含收发线圈姿态角变化的一次项误差,其中Gpxy、Gpyx线圈架构与收发线圈偏航角γ的变化成线性关系,Gpxz、Gpzx线圈架构与收发线圈俯仰角β的变化成线性关系,Gpyz、Gpzy线圈架构与收发线圈摇摆角α的变化成线性关系;而Gpxx、Gpyy、Gpzz线圈架构的一次场误差中不包含有收发线圈姿态角变化的一次项误差。
2.2 二次场误差由9种线圈架构下二次场的求取公式(式(2))可知,二次场误差主要受收发距ρ、收发线圈高度|zr|及h、系统发射频率与大地电导率乘积的影响。
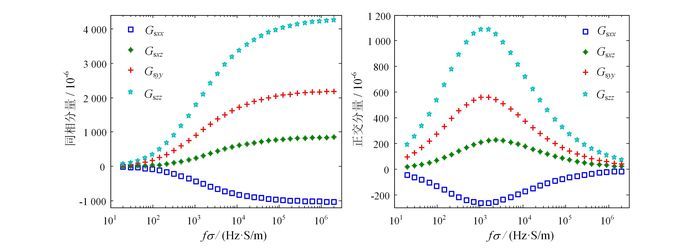
由于采用相对误差来分析二次场误差,需要给出RESOLVE航空宽频带频率域电磁法仪器在4种线圈架构下接收到的二次场与一次场的比值(以10-6值为单位)随fσ的变化,结果如图 5所示。由图 5可知,在系统高度(30 m)远大于收发距(7.9 m)时,满足Gsxx、Gszz线圈架构的二次场幅度值分别是Gsyy线圈架构二次场幅度值的0.5倍、2倍[19, 25],且Gsxz线圈架构二次场幅度值最小。
|
| 图 5 4种线圈架构下二次场的同相分量与正交分量曲线 Figure 5 Inphase and quadrature components of four coil configurations' secondary field |
|
|
将Gsxx, Gsxz, Gsyy, Gszz 4种线圈架构的二次场求取公式对接收线圈高度zr求导,并取差分,得
 (13)
(13) 由于收发线圈是以高度和(即zr-h)的形式出现,可知当收发线圈的高度均发生变化时,若其高度和不变,所产生的二次场值不会发生改变,而当收发线圈同时增加或减少相同高度时,相较于仅有接收线圈高度的变化,将产生两倍的相对误差。
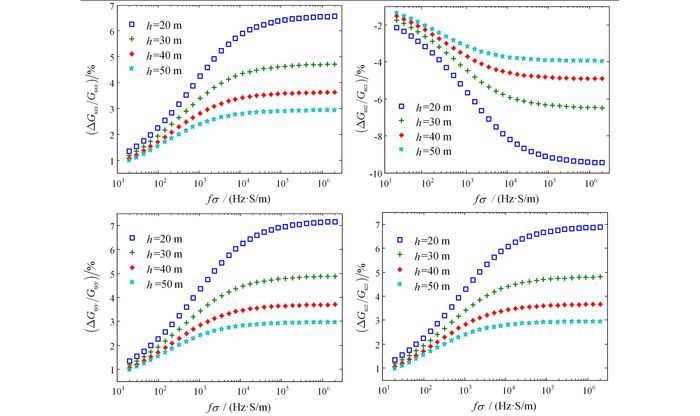
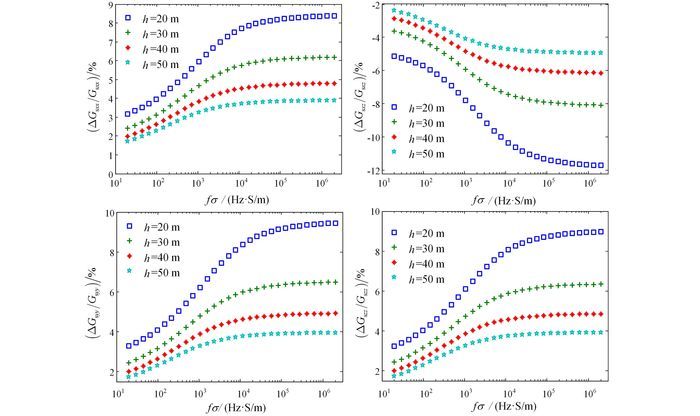
如图 6、7所示, Gsxx、Gsxz、Gsyy、Gszz 4种线圈架构同相分量与正交分量的相对误差幅度均随着系统高度的增加而减小,随着频率电导率乘积的增加先快速而后缓慢的增大,并逐渐趋于平稳,最大分别可以达到8.37%、-11.70%、9.45%、8.97%。若收发线圈的高度同时增大或减小1 m,这种情况在航空频率域电磁法仪器飞行当中时常发生,此时产生的误差是接收线圈高度变化1 m的两倍。可知,高度变化引起的相对误差很大,需通过实时测量并校正。
|
| 图 6 不同高度、接收线圈高度变化1 m时,4种线圈架构二次场同相分量的相对误差 Figure 6 Inphase component relative errors of the four configurations' secondary field, with the receiver coil's height change of 1 m in different heights |
|
|
|
| 图 7 不同高度、接收线圈高度变化1 m时,4种线圈架构二次场正交分量的相对误差 Figure 7 Quadrature component relative errors of the four configurations' secondary field, with the receiver coil's height change of 1 m in different heights |
|
|
由于收发距为收发线圈的水平间距,因此收发距的变化包括收发线圈x轴向上的位置变化和y轴向上的位置变化两种。将Gsxx、Gsxz、Gsyy、Gszz 4种线圈架构的二次场分别对xr、yr求导可知,yr的微小变化引起的二次场误差均为二次或更高次项误差,可以忽略。这里仅保留xr的导数,取微分得
 (14)
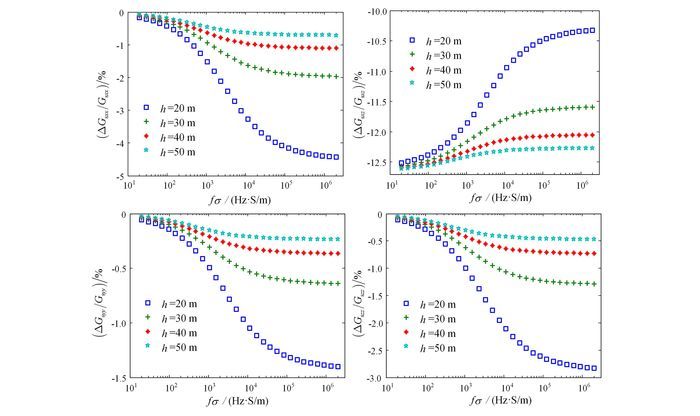
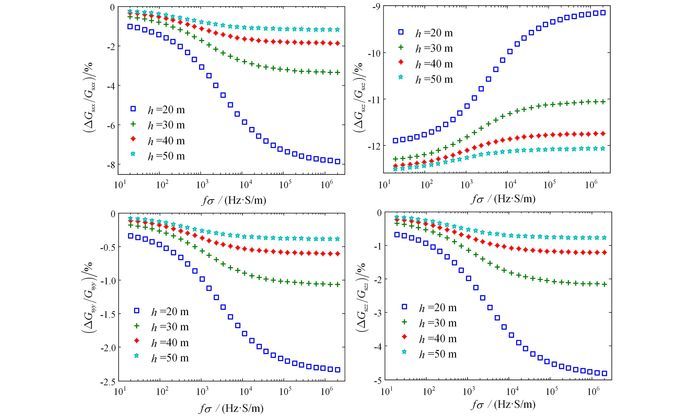
(14) 如图 8、9所示:Gsxx、Gsyy、Gszz线圈架构下二次场同相分量及正交分量的相对误差幅度均随着系统高度的增大而减小,而随着fσ的增大而先快速而后缓慢地增大,并趋于平坦,最大分别可以达到-7.85%、-2.34%、-4.81%;而Gsxz线圈架构下二次场同相分量及正交分量的相对误差幅度随着仪器系统高度的增大而增大,而随着fσ的增大先快而后缓慢地减小,并趋于平坦,最大可以达到-12.51%。其中,Gsyy线圈架构的相对误差幅度最小,而Gsxz线圈架构的相对误差幅度最大。
|
| 图 8 不同高度、收发距变化为1 m时,4种线圈架构下二次场同相分量的相对误差 Figure 8 Inphase component relative errors of the four configurations' secondary field, with the coil separation change of 1 m in different heights |
|
|
|
| 图 9 不同高度、收发距变化为1 m时,4种线圈架构下二次场正交分量的相对误差 Figure 9 Quadrature component relative errors of the four configurations' secondary field, with the coil separation change of 1 m in different heights |
|
|
Yin等[19]分析校正了VCA、VCP、HCP 3种线圈架构的收发线圈绕相同轴向旋转较大姿态角引起的二次场误差。与之不同,本文分析收发线圈姿态角单独变化且变化较小时引入的二次场误差。这一情况常见于系统的安装误差和探测过程中收发线圈发生形变时引入的误差。
在收发线圈的姿态角分别发生变化的情况下,接收线圈接收到的二次场误差为
 (15)
(15) 已知Gsxy, Gsyx, Gsyz, Gszy=0,在忽略姿态角变化的二次及高次项误差的情况下,式(15) 可化简为
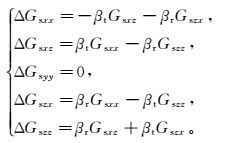 (16)
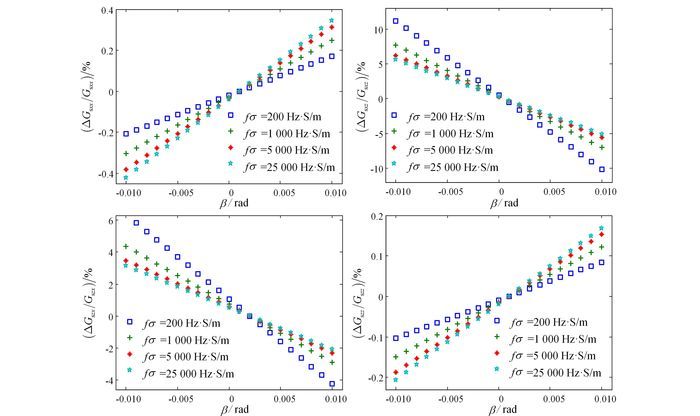
(16) 由式(16) 可知,Gsxx、Gsxz、Gszx、Gszz线圈架构仅受收发线圈俯仰角β变化的影响,而Gsyy线圈架构则不受较小角度变化的影响。在满足Gsxz=-Gszx的情况下,由收发线圈姿态角变化引起误差的对称关系,只需仿真接收线圈姿态角变化对二次场误差的影响,此时βt=0.001 rad,结果如图 10、11所示。
|
| 图 10 频率电导率乘积不同、俯仰角变化时,4种线圈架构下二次场同相分量的相对误差 Figure 10 Inphase component relative errors of the four configurations' secondary field, with the change of pitch rotation and different frequency-conductivity products |
|
|
|
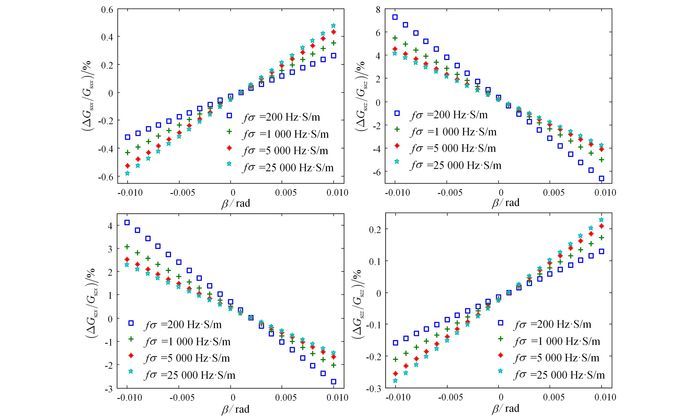
| 图 11 频率电导率乘积不同、俯仰角变化时,4种线圈架构下二次场正交分量的相对误差 Figure 11 Quadrature component relative errors of the four configurations' secondary field, with the change of pitch rotation and different frequency-conductivity products |
|
|
由图 10、图 11可知,Gsxx、Gszz线圈架构的同相分量与正交分量的相对误差幅度均随着收发线圈俯仰角β的增大先线性降低而后线性增大,随着fσ的增大而增大,最大分别可以达到-0.58%、-0.28%。Gsxz、Gszx线圈架构的同相分量与正交分量的相对误差幅度均随着收发线圈俯仰角β的增大先线性降低而后线性增大,随着fσ的增大而减小。Gsxz、Gszx线圈架构的相对误差幅度最大,最大可以达到11.2%。
需要指出的是,式(16) 是在忽略姿态角变化的二次及高次项误差时得到的;当姿态角变化较大时,二次及高次项误差则不能忽略,需要测量相应的姿态角信息(此时还包括摇摆角α),对系统测得的二次场进行校正[19-21]。
3 结论与讨论本文首先对9种线圈架构的接收线圈在均匀大地模型下接收到的一次场及二次场分别进行建模,并以Fugro公司的RESOLVE系统参数为例,对9种线圈架构由于收发线圈位置、姿态角变化引起的一次场误差及二次场误差在均匀大地模型下进行了定量分析。其中一次场误差仅能影响二次场的同相分量。经过分析可以得出以下结论:
1) 由于收发线圈位置变化,一次场引入的误差中,仅PERyz、PERzy线圈架构中不包含位置变化的一次项误差。
2) 由于收发线圈姿态角变化,一次场引入的误差中,仅VCA、VCP、HCP线圈架构不包含姿态角变化的一次项误差。
3) 仪器的飞行高度变化1 m时,二次场引入的误差中, VCA、VCP、HCP、PERxz、PERzx线圈架构二次场同相分量与正交分量的相对误差均很大,因此需要实时测量系统的飞行高度并校正。其中以PERxz、PERzx线圈架构为最大。
4) 仪器的收发距变化1 m时,二次场引入的误差中,VCA、VCP、HCP、PERxz、PERzx线圈架构二次场同相分量与正交分量的相对误差均很大,因此需要实时测量系统的收发距并校正。其中以PERxz、PERxz线圈架构为最大,VCP线圈架构为最小。
5) 在收发线圈姿态角单独变化且变化较小时,VCA、VCP、HCP、PERxz、PERzx线圈架构引入的二次场误差仅与俯仰角β的变化有关。其中PERxz、PERxz线圈架构为最大,VCP线圈架构为最小。
本文对几何误差的定量分析在基于磁偶极子模型的频率域电磁法仪器制作、校正以及野外实验操作方面具有很强的指导意义。在野外实验操作时,对于引起二次项误差的几何形变,如果变化较小时,则可以忽略;在进行仪器校正时,对引起一次项误差或较大二次项误差的几何形变则需要进行建模,可以参考磁通门传感器偏置、线性度以及三轴正交度等参数的旋转校正算法予以校正[26-27],而该部分将是作者下一步的主要研究内容,这里不再详细叙述。
致谢: 中国科学院电子学研究所的齐有政博士、张建国博士在软件编程方面给予了耐心讲解与帮助,在此表示衷心感谢。| [1] | Fraser D C. The Multicoil: Ⅱ: Airborne Electro-magnetic System[J]. Geophysics, 1979, 44(8): 1367-1394. DOI:10.1190/1.1441013 |
| [2] | Fraser D C. Dighem Resistivity Techniques in Airborne Electromagnetic Mapping[J]. Geological Survey of Canada, 1986, 22: 49-54. |
| [3] | Cain M J. ResolveSurvey for US Geological Survey East Poplar Oil Fields[R]. Montana: Fugro Airborne Surveys, 2004. |
| [4] | Won I J, Oren A, Funak F. GEM-2A: A Programmable Broadband Helicopter-Towed Electromagnetic Sensor[J]. Geophysics, 2003, 68(6): 1888-1895. DOI:10.1190/1.1635041 |
| [5] | McNeill J D. EM34-3 Measurements at Two Inter-Coil Spacings to Reduce Sensitivity to Near-Surface Material[R]. Mississauga: Geonics, 1985. |
| [6] | McNeill J D. Why Doesn't Geonics Limited Build a Multi-Frequency EM31 or EM38?[R]. Mississauga: Geonics, 1996. |
| [7] | McNeill J D. Electromagnetic Terrain Conductivity Measurement at Low Induction Numbers[R]. Mississauga: Geonics, 1980. |
| [8] | Won I J, Keiswetter D A, Fields G R A, et al. GEM-2: A New Multifrequency Electromagnetic Sensor[J]. Journal of Environmental and Engineering Geophysics, 1996, 1(2): 129-137. DOI:10.4133/JEEG1.2.129 |
| [9] | Won I J, Keiswetter D A, Hanson D R, et al. GEM-3: AMonostatic Broadband Electromagnetic Induction Sensor[J]. Journal of Environmental and Engineering Geophysics, 1997, 2(1): 53-64. DOI:10.4133/JEEG2.1.53 |
| [10] | Huang H, San Filipo B, Oren A, et al. Coaxial Coil Towed EMI Sensor Array for UXO Detection and Characterization[J]. Journal of Applied Geophysics, 2007, 61(3): 217-226. |
| [11] | Manstein Y, Manstein A. EM-ISensor NEMFIS: Method, Equipment and Case Stories of Archaeological Prospection[J]. ArcheoSciences, 2009, 33: 321-324. |
| [12] | Tølbøll R J, Christensen N B. Sensitivity Functions of Frequency-Domain Magnetic Dipole-Dipole Systems[J]. Geophysics, 2007, 72(2): F45-F56. DOI:10.1190/1.2409623 |
| [13] | Ward S H, Hohmann G W. Electromagnetic Theory for Geophysical Applications[M]. Tulsa: Society of Exploration Geophysicists, 1988: 131-311. |
| [14] |
王卫平, 曾昭发, 李静, 等. 频率域航空电磁法地形影响和校正方法[J].
吉林大学学报(地球科学版), 2015, 45(3): 941-951.
Wang Weiping, Zeng Zhaofa, Li Jing, et al. Topographic Effects and Correction for Frequency Airborne Electromagnetic Method[J]. Journal of Jilin University (Earth Science Edition), 2015, 45(3): 941-951. |
| [15] | Son K H. Interpretation of Electromagnetic Dipole-Dipole Frequency Sounding Data over a Vertically Stratified Earth[D]. North Carolina: North Carolina State University, 1985. |
| [16] | Won I J, Smits K. Airborne Electromagnetic Bathymetry[J]. Geoexploration, 1991, 27(3): 297-319. |
| [17] | Holladay J S, Lo B, Prinsenberg S K. Bird Orientation Effects in Quantitative Airborne Electromagnetic Interpretation of Pack Ice Thickness Sounding[C]//Oceans'97 MTS/IEEE Conference Proceedings. Halifax: [s. n.], 1997: 1114-1119. |
| [18] | Balkov E V, Epov M I, Manstein A K, et al. Elements of Calibration and Data Interpretation of EMI Sounding Device EMS[C]//The 10th European Meeting of Environmental and Engineering Geophysics. Utrecht: Near Surface, 2004. |
| [19] | Yin C, Fraser D C. Attitude Corrections of Helicopter EM Data Using a Superposed Dipole Model[J]. Geophysics, 2004, 69(2): 431-439. DOI:10.1190/1.1707063 |
| [20] |
王琦, 林君, 于生宝, 等. 固定翼航空电磁系统的线圈姿态及吊舱摆动影响研究与校正[J].
地球物理学报, 2013, 56(11): 3741-3750.
Wang Qi, Lin Jun, Yu Shengbao, et al. Study on Influence and Correction of Coil Attitude and Bird Swing for the Fixed-Wing Time-Domain Electromagnetic System[J]. Chinese Journal of Geophysics, 2013, 56(11): 3741-3750. DOI:10.6038/cjg20131115 |
| [21] |
曲昕馨, 李桐林, 王飞. 直升机吊舱姿态变化对电磁场测量的影响规律及其校正方法研究[J].
地球物理学报, 2014, 57(4): 1310-1321.
Qu Xinxin, Li Tonglin, Wang Fei. A Study on the Effect of Bird's Attitude on Helicopter EM Data and the Correction Method[J]. Chinese Journal of Geophysics, 2014, 57(4): 1310-1321. DOI:10.6038/cjg20140428 |
| [22] | Lin J. Sensitivity Analysis and Comparison of Frequency-Domain Electromagnetic System Configurations[C]//International Symposium on Antennas, Propagation and EM Theory, 2000 Proceedings. Isape: IEEE Xplore, 2000: 630-633. |
| [23] | Guillemoteau J, Sailhac P, Behaegel M. Modelling an Arbitrarily Oriented Magnetic Dipole over a Homogeneous Half-Space for a Rapid Topographic Correction of Airborne EM Data[J]. Exploration Geophysics, 2015, 46(1): 85-96. DOI:10.1071/EG13093 |
| [24] | West G F, Macnae J C. Physics of the Electroma-gnetic Induction Exploration Method: Electromagnetic Methods in Applied Geophysics: Applications: Part A and Part B[M]. Tulsa: Society of Exploration Geophysicists, 1991: 5-45. |
| [25] | Frischknecht F C, Labson V F, Spies B R, et al. Profiling Methods Using Small Sources[M]. Tulsa: Society of Exploration Geophysicists, 1991: 105-270. |
| [26] | Bracken R E, Smith D V, Brown P J, et al. Calibrating a Tensor Magnetic Gradiometer Using Spin Data[R]. Reston: US Geological Survey, 2005. |
| [27] | Pang H, Li J, Chen D, et al. Calibration of Three-Axis Fluxgate Magnetometers with Nonlinear Least Square Method[J]. Measurement, 2013, 46(4): 1600-1606. DOI:10.1016/j.measurement.2012.11.001 |


