2. 中国石油渤海钻探工程有限公司测井分公司, 天津 300280
2. Logging Branch of CNPC Bohai Drilling Engineering CO. LTD., Tianjin 300280, China
0 引言
钻井过程中,井内泥浆液柱和地层之间通常存在压差,在压差的作用下泥浆滤液侵入渗透性地层。泥浆侵入过程中,由于泥浆滤液的渗滤性质、侵入压差、油水相对渗透率、泥浆滤液与地层水矿化度差异以及泥浆滤液侵入储层的时间等因素的影响,井眼周围地层的压力、流体饱和度、矿化度和井周的电阻率发生变化,造成储集层电测井响应特征在一定程度上不能反映原状地层的真实情况,给油水层的准确判断带来困难。因此,认识和掌握泥浆滤液侵入特征,对储层的精确评价具有重要作用。
随着石油勘探开发的不断发展,测井仪器设计和解释方法方面也取得了很大进展,但由于地下储层不同流体相的渗流机理差异,加上泥浆侵入过程本身的复杂性,对泥浆侵入过程特征的探索研究仍存在难点。近年来国内外很多专家在探明泥浆滤液侵入对地层特征影响方面做了大量研究工作。张松扬等[1]、黄龙等[2]、刘尊年等[3]从泥浆侵入机理角度分析,阐述了泥浆侵入的影响因素及侵入对测井响应的影响,为储层精确评价提供了参考。陈福煊等[4]根据模拟理论设计泥浆侵入实验,获得了泥浆滤液侵入油层、气层和水层的径向侵入剖面,为准确评价储层提供了实验依据。张建华等[5]、Mark等[6]、Won等[7]、徐文远等[8]、Malik等[9]、常文会等[10]采用数值模拟方法,从储层物性、侵入压差、流体性质、侵入时间等方面对泥浆侵入特征及地层电阻率变化特征做了影响因素分析,为储层描述和测井解释提供了理论依据。Wu等[11]、杨振等[12]、邓少贵等[13]应用数值模拟方法,对斜井、水平井等情况下泥浆侵入特性及井眼周围电性变化进行了深入研究,有助于斜井储层的评价。Dewan等[14]、范宜仁等[15]、Ling等[16]在研究泥浆侵入特性时着重考虑了泥饼特性对侵入规律的影响作用。Tobola等[17]利用数值方法,模拟了地层泥浆侵入过程井周侵入带的动态变化,并对时间推移测井响应变化特征进行分析研究,提出了评价地层渗透性的方法。邓少贵等[18]、范文同等[19]、任好等[20]根据泥浆侵入机理及侵入特征,采用数值模拟方法对双感应、阵列感应等测井响应进行电阻率校正,取得了较好的效果。
目前,大部分泥浆侵入研究成果没有把侵入特征与阵列感应测井响应特征有机结合起来, 进行储层流体性质识别与电阻率校正。本文针对大港某地区实际储层特点,基于油藏流体流动满足的质量守恒定律和达西定律,采用数值模拟方法[21],研究泥浆侵入过程中地层含水饱和度、矿化度及地层电阻率的动态变化情况,以及泥浆侵入后井周油藏的分布情况; 并结合对实例井的模拟,分析侵入特征与阵列感应电测井响应之间的关系,并提出有效的电阻率校正方法,以期为准确的储层性质评价提供可靠依据。
1 泥浆侵入理论模型 1.1 油水两相渗流有限差分模型模拟假设地层中只有油相和水相,认为油水两相不混溶,考虑重力和毛管压力影响,考虑流体和岩石的压缩性。泥浆侵入过程中流体渗流遵循质量守恒定律,油水两相质量平衡方程为:
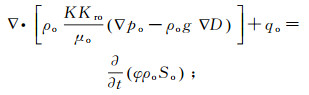 (1)
(1) 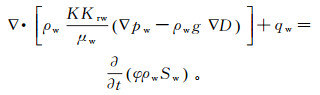 (2)
(2) 式中:K为地层渗透率;Kro和Krw分别为油相和水相的相对渗透率;ρo和ρw分别为油和水的密度;μo和μw分别为油和水的黏度;po和pw分别为油相和水相压力;g为重力加速度;D为地层深度;qo和qw分别为油、水流量;φ为地层孔隙度;So和Sw分别为含油饱和度和含水饱和度;t为泥浆滤液侵入时间。
辅助方程为:
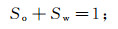 (3)
(3) 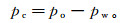 (4)
(4) 式中:pc为油、水两相间的毛管压力,是Sw的函数。
模型初始条件为:
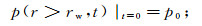 (5)
(5) 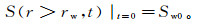 (6)
(6) 式中:p0为初始地层压力;Sw0为初始地层含水饱和度;r为地层径向半径;rw为井眼半径。
模型边界条件采用内边界定压条件、外边界封闭条件:
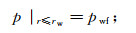 (7)
(7) 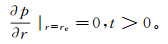 (8)
(8) 式中:pwf为井底流压;re为地层外边界。
1.2 不同矿化度水对流扩散模型泥浆侵入过程中,当泥浆滤液矿化度与地层水矿化度存在差异时,泥浆滤液与地层水会发生对流扩散,遵循的方程为
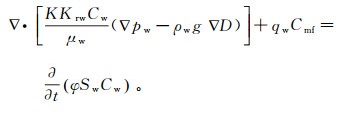 (9)
(9) 式中:Cw为地层水矿化度;Cmf为泥浆滤液矿化度。根据不同时刻储层压力和饱和度分布情况,可得到不同时刻地层水矿化度的分布状态。
1.3 电性参数计算公式根据侵入后地层水矿化度分布,可计算不同时刻距离井轴为r的地层水电阻率Rw(r, t):
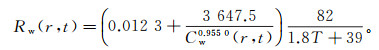 (10)
(10) 式中:Cw(r, t)为侵入时间为t、距离井轴为r的地层水矿化度;T为地层温度。
根据前面得到的地层含水饱和度和地层水电阻率随时间的分布,可应用阿尔奇公式确定不同侵入时刻距离井轴为r的地层电阻率Rt(r, t):
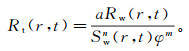 (11)
(11) 式中:Sw(r, t)为侵入时间t距离井轴为r的地层含水饱和度;a为岩性指数;m为胶结指数;n为饱和度指数。
1.4 泥饼渗透率参数计算公式泥浆滤液侵入到渗透性地层的同时,泥浆中固相颗粒在近井壁处逐渐沉积并形成一层渗透性很差的泥饼,泥饼渗透率很低,是影响泥浆侵入的主要因素之一。Tobola等[5]、Zhang等[22]研究认为泥饼渗透率随侵入时间呈指数下降,文中模拟时引用如下经验公式[1, 22]计算泥饼渗透率Kmc:
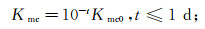 (12)
(12) 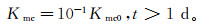 (13)
(13) 式中,Kmc0为泥饼初始渗透率。模拟过程中假设泥饼形成稳定时渗透率不再随时间变化。
2 泥浆侵入数值模拟地层模型本研究基于泥浆侵入地层机理,采用有限差分数值模拟方法[23]建立地层模型,模拟泥浆滤液侵入过程储层流体饱和度、地层水矿化度和地层电阻率等参数随侵入时间变化的径向和垂向分布特征。
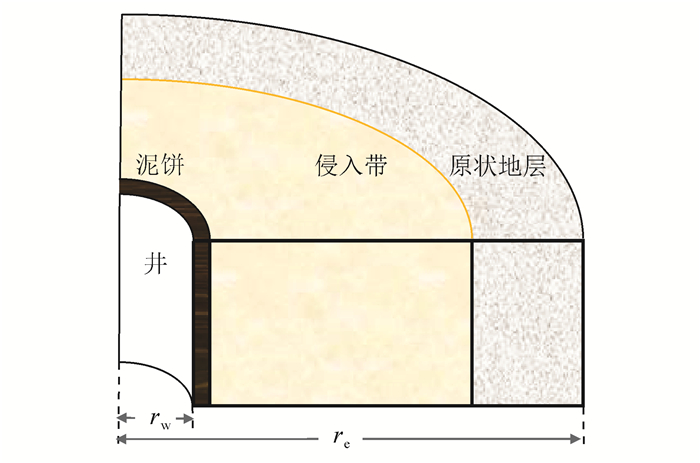
泥浆侵入数值模拟地层模型考虑垂直井情况,选用径向坐标,采用径向和垂向均匀网格划分。参考研究区实际储层物性特征、流体特征及生产动态特性资料,模型中具体参数设置为:rw=0.1 m,re=6.1 m,Sw0=0.4,岩石压缩系数为5.8×10-4 MPa-1,地层水压缩系数为4.3×10-4 MPa-1,ρw=1.05 g/cm3,ρo=0.83 g/cm3,μw=1.03 mPa·s,μo=1.13 mPa·s,g=9.8 m/s2,Cw=20 000 mg/L,T=105 ℃,井眼与地层之间压差为5 MPa,a=1,m=2,n=2。考虑地层渗透率各向同性。地层模型如图 1所示。
|
| 图 1 泥浆侵入数值模拟地层模型 Figure 1 Numerical simulation formation model of mud invasion |
|
|
泥浆滤液侵入渗透性地层后驱替掉井周地层流体,改变了地层原始流体的分布状态,井周形成侵入带。为研究该地区低渗储层不同渗透率情况下泥浆侵入过程中井周地层特征的变化规律,模拟时参考研究区储层岩心物性分析资料,根据渗透率变化范围,模拟地层渗透率分别为0.3、3.0和30.0 mD①3种典型情况的侵入特征。
① mD (毫达西)为非法定计量单位,1 mD=0.986 9×10-3 μm2,下同。
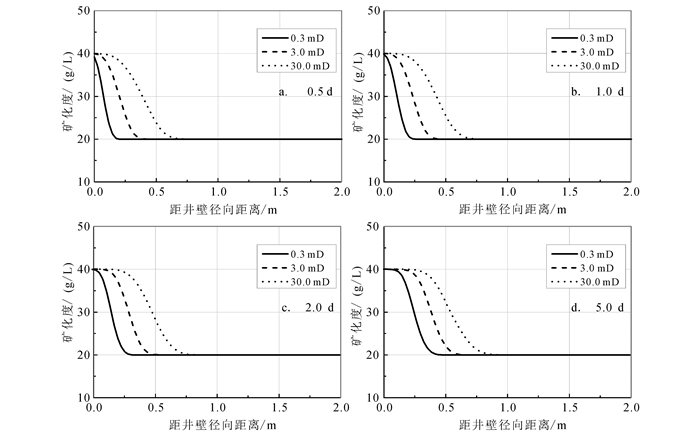
3.1 井周地层水矿化度变化情况模拟时泥浆滤液矿化度为40 000 mg/L,高于地层水矿化度,为盐水泥浆侵入。图 2是泥浆侵入0.5、1.0、2.0和5.0 d后,井周地层水矿化度的径向变化情况。
|
| 图 2 井周矿化度径向分布图 Figure 2 Radial distribution of salinity around the well |
|
|
由于泥浆滤液与地层水矿化度不同,随着侵入现象发生,泥浆滤液与地层水发生物理混合。以t=1.0 d为例,从图 2b中可以看出,随着地层渗透率的增加,泥浆侵入深度增加,矿化度侵入剖面逐渐延伸。从图 2中井周地层水矿化度与侵入深度的关系可以看出,随着侵入时间的增加,3种渗透率情况下的地层矿化度侵入剖面前缘逐渐向远离井眼方向延伸。
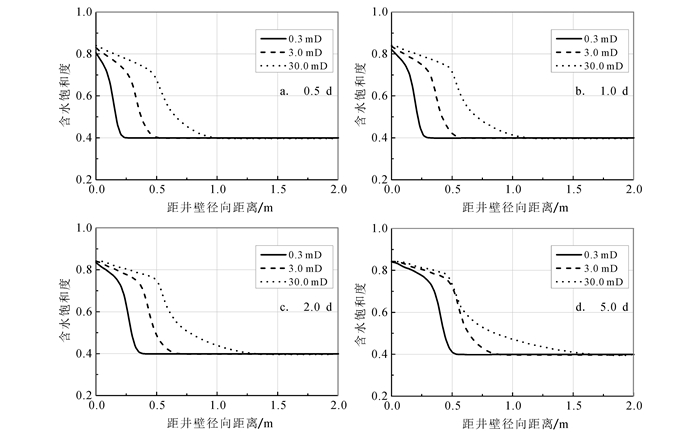
3.2 井周地层含水饱和度变化情况在井眼与地层压力差作用下,泥浆滤液侵入渗透性地层并改变地层流体原始分布状态。图 3是泥浆侵入0.5、1.0、2.0和5.0 d后,井周地层含水饱和度的径向变化情况。以t=1.0 d为例,发生泥浆侵入时,井周地层含水饱和度增加,随着距井眼距离的增加,含水饱和度逐渐降低到地层原始状态。从图 3b中还可以看出,由于储层渗透性的差异,侵入时间相同时,随着地层渗透率由低到高变化,泥浆侵入深度明显呈逐层增加特征。从图 3不同侵入时刻井周含水饱和度与侵入深度的关系可以看出:在侵入初期(t≤2 d时), 随着侵入时间的增加,3种渗透率情况下泥浆侵入深度逐渐增加;在侵入时间达到5.0 d时,从井周含水饱和度变化情况可以看出,30 mD地层含水饱和度侵入剖面没有明显向远离井眼方向延伸。分析认为:一是渗透率较高的地层在泥浆侵入过程中地层压力变化较快,侵入后期井眼与地层压力相差较小或两者达到平衡,此时泥浆侵入程度明显降低;二是渗透率较高的地层在侵入后期泥饼形成并稳定,其渗透率较差,泥浆滤液侵入量也相应降低。
|
| 图 3 井周含水饱和度径向分布图 Figure 3 Radial distribution of water saturation around the well |
|
|
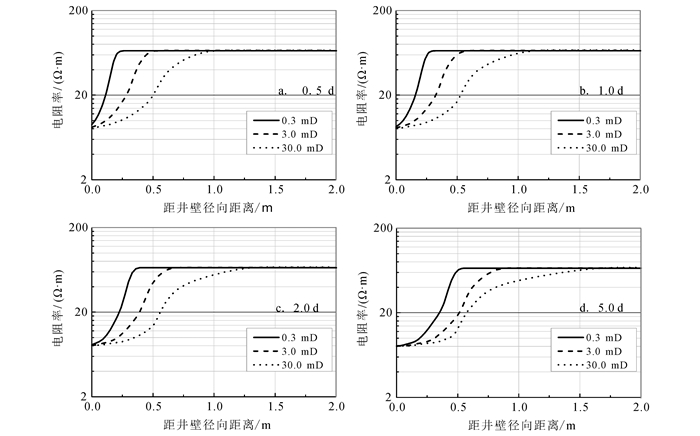
根据前面模拟得到的井周矿化度和含水饱和度变化结果,应用式(10)、(11)计算得到不同侵入时刻下的井周地层电阻率变化结果。图 4是泥浆侵入0.5、1.0、2.0和5.0 d后,井周地层电阻率的径向变化情况。
|
| 图 4 井周电阻率径向分布图 Figure 4 Radial distribution of resistivity around the well |
|
|
从图 4中可以看出,原状地层的电阻率为65 Ω·m,发生盐水泥浆侵入后,井眼附近电阻率降至约8 Ω·m;从模拟结果看出,井周附近地层电阻率呈现明显低侵特征。
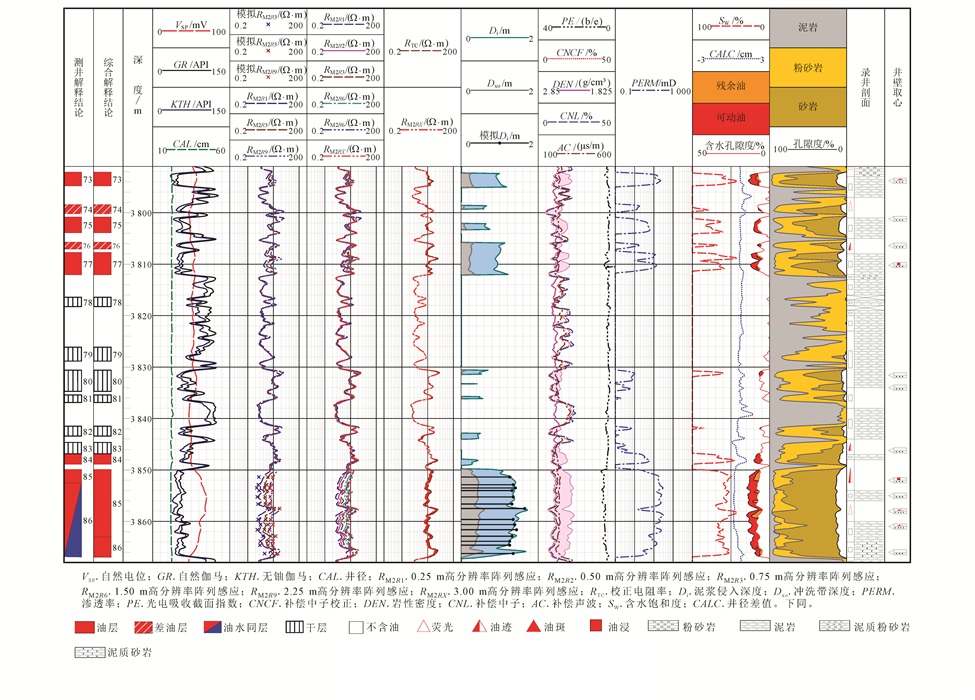
4 泥浆侵入特征实例分析 4.1 实际井泥浆侵入数值模拟研究大港油田某地区属低渗的复杂储层,试井资料显示部分层段存在低阻油层,这给该地区测井解释评价带来了很大困难。图 5是A1X井测井解释成果图,3 850~3 864 m层段解释为油层,6条高分辨率阵列感应测井曲线显示为低值且曲线存在明显的分离,RM2R1 < RM2R2 < RM2R3 < RM2R6 < RM2R9 < RM2RX,分析认为泥浆侵入引起储层低阻。在该层段选取14个小层,根据岩心分析实验数据,选取深度点物性、相对渗透率、毛管压力特征,考虑层段重力分异作用和侵入时间等因素,应用泥浆侵入数值模拟方法,模拟侵入7 d后井周地层的电阻率变化情况及侵入深度。根据模拟得到的侵入深度及侵入带电阻率,应用几何因子理论计算得出相应深度层段的阵列感应电阻率值[24-25]。从图 5第八道中侵入深度的模拟结果可以看出,该层段泥浆侵入深度为1.5 m左右。在图 5第五道中,×代表模拟计算的阵列感应电阻率响应值,曲线代表实测的阵列感应电阻率值,可以看出两者的对应关系较好。
|
| 图 5 AIX并测并解释成果图 Figure 5 Log interpretation graph of well AIX |
|
|
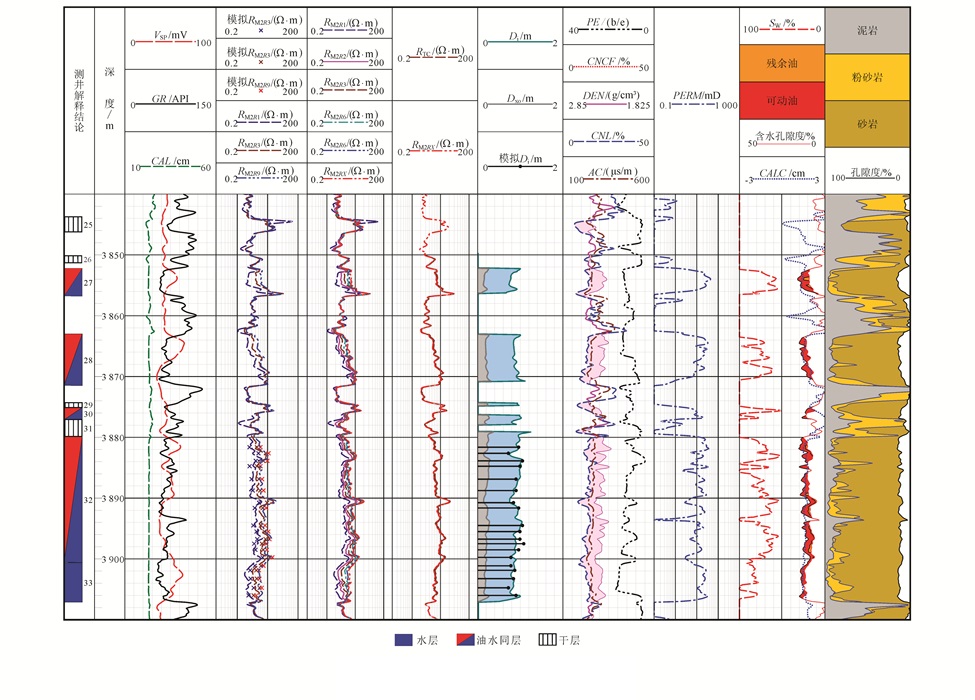
图 6是Z1X井测井解释成果图,3 880~3 890 m层段试油结果为油水同层,6条高分辨率阵列感应测井曲线显示为低值且存在分离,RM2R1 < RM2R2 < RM2R3 < RM2R6 < RM2R9≈RM2RX,RM2R9和RM2RX曲线几乎重合。在该层段选取19个小层,根据储层特征及测井信息资料,应用泥浆侵入数值模拟方法,模拟侵入5 d后井周地层的电阻率变化情况及侵入深度。从模拟结果看出,该层段泥浆侵入深度为0.9 m左右,计算得到的视电阻率值与实测电阻率值在部分层段有差别,整体上两者的变化趋势较一致。
|
| 图 6 Z1X并测井解释成果图 Figure 6 Log interpretation graph of well ZIX |
|
|
图 7是C1X井测井解释成果图,在3 920~3 936 m深度段107-110层段解释结论为干层,该深度段6条高分辨率阵列感应测井曲线几乎重合。在该层段选取9个小层,根据储层特征及测井信息资料,应用泥浆侵入数值模拟方法,模拟侵入4 d后井周地层的电阻率变化情况及侵入深度。从模拟结果看出,该层段泥浆侵入深度为0.1 m左右,通过模拟计算得到的视电阻率值几乎重合,与实测电阻率值相差很小。

|
| 图 7 CIX并测并解释成果图 Figure 7 Log interpretation graph of well C1X |
|
|
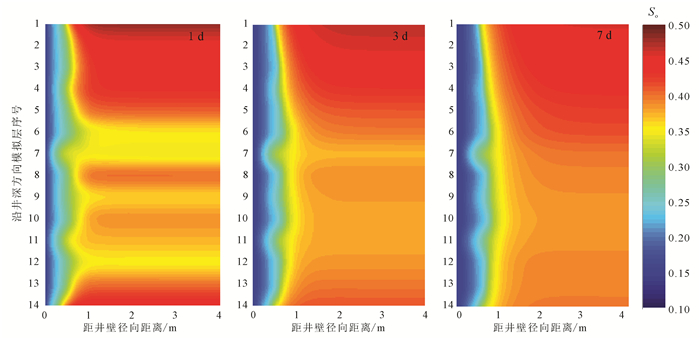
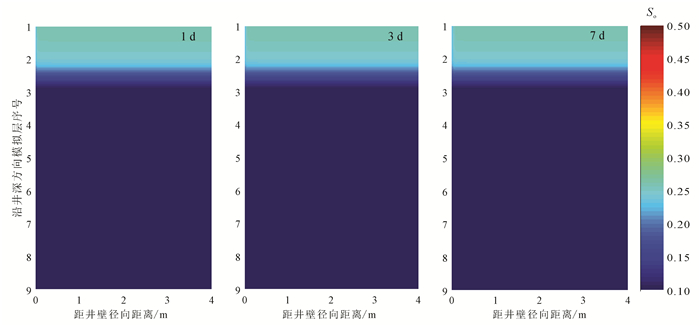
为研究泥浆侵入地层后井周油藏的分布特征及其与储层流体性质的关系,本文对上面3口实际井模拟层段的井周油藏分布特征进行深入分析。图 8、图 9、图 10分别是A1X井、Z1X井和C1X井在侵入时间为1、3和7 d时井周油相的分布状态。从井周储层油藏分布模拟结果,得到以下认识:
|
| 图 8 A1X井不同侵入时刻井周油藏动态演化规律示意图 Figure 8 Dynamic evolution diagram of reservoir around well A1X at different invasion time |
|
|

|
| 图 9 Z1X井不同侵入时刻井周油藏动态演化规律示意图 Figure 9 Dynamic evolution diagram of reservoir around well Z1X at different invasion time |
|
|
|
| 图 10 C1X井不同侵入时刻井周油藏动态演化规律示意图 Figure 10 Dynamic evolution diagram of reservoir around well C1X at different invasion time |
|
|
1) 泥浆侵入数值模拟能够很好地揭示侵入过程中井周地层的油藏动态演化规律。从图 8-10中可以看出,在泥浆侵入过程中,泥浆滤液进入地层后改变了井周流体的原始分布状态,井周附近的含油饱和度降低,由井眼向地层方向饱和度逐渐增加到地层原始含油饱和度。
2) 图 8是A1X井下部油层层段模拟结果,整个层段的初始含油饱和度有一定差异(根据含水饱和度曲线可知该层段底部含油饱和度略高于中部含油饱和度)。从模拟结果可以看出:随着侵入时间的增加,近井周处,储层含油饱和度较小,与初始地层含油饱和度值相比变化较大;从整个层段上看,层段中下部含油饱和度降低较明显,主要是由于模拟时考虑储层各向同性,侵入时间较长时重力分异作用导致储层下部含水量增加。图 9模拟井层段上部为油水同层,下部为水层。从图 9中可以看出:泥浆侵入过程中,油水同层层段井周油藏变化相对明显,而水层层段含油饱和度变化不明显,与原始地层的含油饱和度相差不大;且储层饱和度变化情况能够清晰地显示出层段的油水界面,模拟结果可以提高储层油水界面划分的准确性。图 10模拟井层段为干层。干层的物性差,内部孔隙连通性差,模拟结果显示泥浆侵入深度很小,随着侵入时间的增加,井周油藏分布几乎没有变化。
对比3口井不同侵入时刻井周油藏动态演化规律示意图发现,泥浆侵入后,随着侵入时间的增加,油层层段井周油藏分布变化最大,含油饱和度降低较明显,油水同层次之,水层变化很小,干层几乎没有变化;可以说井周油藏的变化情况与储层流体性质有明显关系。
5 阵列感应测井电阻率校正方法根据6条阵列感应测井曲线的响应特征,结合实际井泥浆侵入数值模拟结果,分析认为6条阵列感应测井曲线的分离程度与泥浆侵入深度Di密切相关:当6条曲线分离不明显、几乎达到重合时,Di值很小或接近于0;当深探测深度的阵列感应测井曲线(如2.25 m和3 m探测深度测井曲线)出现重合时,Di值增大,此时侵入剖面出现冲洗带;当不同探测深度的阵列感应曲线出现明显分离时,Di值更大。因此,根据Di与阵列感应曲线特征关系,构建Di与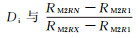
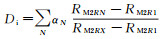
根据前面实际井泥浆侵入模拟结果,将模拟层段的侵入深度和阵列感应测井值建立方程组,经多元回归确定系数αN,系数α2、α3、α6、α9分别为2.85,-3.28,-0.71,2.71。由此,可确定整个井段泥浆Di的计算公式。
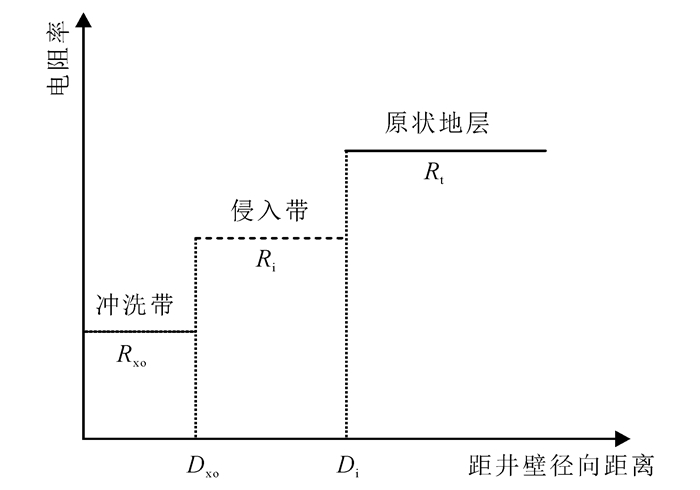
盐水泥浆侵入地层后井周地层电阻率分布为阶跃模型,采用5个参数(Rxo(冲洗带电阻率)、Dxo、Ri(侵入带电阻率)、Di、Rt)来描述地层侵入剖面情况,如图 11所示。
|
| 图 11 侵入阶跃模型 Figure 11 Step model for invasion |
|
|
根据径向伪几何因子,按照侵入阶跃模型计算的原状地层电阻率为
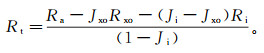 (13)
(13) 式中,Jxo、Ji分别为Dxo、Di对应的横向积分几何因子。
利用本文建立的方法对研究区实际井资料进行处理,以选取模拟的3口井为例。图 5-7中Di、Dxo曲线为采用上述方法计算得到的泥浆侵入带深度和冲洗带深度。从图 5-7中可看出阵列感应测井响应特征与侵入阶跃剖面的变化情况;校正电阻率RTC为采用5参数方法计算的储层侵入初始时刻的电阻率曲线。通过对实际井的处理,对比发现:当6条阵列感应曲线明显分离时,形成明显的冲洗带和侵入带,电阻率校正量约为2~3 Ω·m;当2.25 m和3 m阵列感应曲线出现重合时,冲洗带和侵入带深度减小,电阻率校正量约为0.2~1.2 Ω·m;当6条阵列感应曲线接近重合时,此时侵入剖面不存在冲洗带且侵入带深度很小,电阻率校正量约为0。对比3口井的电阻率校正情况发现,阵列感应曲线分离越明显,泥浆侵入越深,储层电阻率校正幅度越大。当深探测深度的阵列感应曲线出现重合时,3 m探测深度的感应测井曲线与原状地层的电阻率十分接近,可以很好地反映地层电阻率的变化情况。
本研究中将泥浆侵入特征和阵列感应测井曲线分离特征结合起来建立的电阻率校正方法,有效地隐去了侵入时间的影响因素;实际应用时,对不同侵入时刻的电测井曲线均有很好的应用效果。
6 结论本文依据油藏中油水两相流体的渗流理论,应用数值模拟方法构建地层模型,研究低渗储层井周地层泥浆侵入特征及油藏分布特征,并建立了阵列感应电阻率校正方法。通过模拟得出以下结论:
1) 低渗储层的岩石渗透性、流体饱和度、泥浆及地层水矿化度、侵入时间等因素对泥浆侵入后井周地层电阻率变化具有明显影响。
2) 在低渗储层泥浆侵入过程中,在相同的侵入时间内,随着地层渗透率增加,泥浆侵入深度增加;在高矿化度泥浆侵入油层后,井周地层水矿化度增加,含水饱和度增加,电阻率降低,储层呈现明显低侵剖面。
3) 根据阵列感应测井曲线的分离情况,对3口井进行泥浆侵入数值模拟,结果表明泥浆侵入时间和侵入深度是对阵列感应测井响应特征及其电阻率的幅度差异重要影响因素。将侵入特征与阵列感应测井响应特征有机结合,可更好地对储层流体进行识别,有助于提高电测井评价储层的准确性。
4) 泥浆侵入后井周油藏动态分布模拟结果显示,随着侵入时间的增加,油层层段井周油藏分布变化最大,含油饱和度降低较明显,油水同层次之,水层变化很小,干层几乎没有变化;可以说明井周油藏的变化情况与储层流体性质有明显关系。
5) 结合泥浆侵入特征模拟实例与阵列感应测井响应特征,在利用阵列感应测井曲线分离程度构建侵入深度计算模型的基础上,根据侵入剖面特征应用积分几何因子理论建立电阻率校正公式,经实际井处理,阵列感应曲线分离越明显,泥浆侵入越深,储层电阻率校正幅度越大。
| [1] | 张松扬, 陈玉魁. 钻井液侵入机理特征及影响因素研究[J]. 勘探地球物理进展, 2002, 25 (6) : 28-31. Zhang Songyang, Chen Yukui. Reponses to Drilling-Fluid[J]. Progress in Exploration Geophysics, 2002, 25 (6) : 28-31. |
| [2] | 黄龙, 鲍志东, 张文瑞, 等. 淡水泥浆侵入引起的低阻油气层实例分析[J]. 西南石油大学学报(自然科学版), 2008, 30 (2) : 14-18. Huang Long, Bao Zhidong, Zhang Wenrui, et al. Case Study on Low Resistivity Oil & Gas Zone Caused by Fresh Water Mud Invasion[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2008, 30 (2) : 14-18. |
| [3] | 刘尊年, 孙建孟, 迟秀荣, 等. 泥浆侵入研究现状分析[J]. 地球物理学进展, 2012, 27 (6) : 2594-2599. Liu Zunnian, Sun Jianmeng, Chi Xiurong, et al. Analysis of Research Present Situation of Mud Invasion[J]. Progress in Geophysics, 2012, 27 (6) : 2594-2599. |
| [4] | 陈福煊, 孙嘉戌. 泥浆滤液侵入孔隙地层径向导电特性的模拟实验[J]. 地球物理学报, 1996, 39 (增刊1) : 371-378. Chen Fuxuan, Sun Jiaxu. Simulation Test of Radial Electric Conductivity During the Mud Filtrate Invading Porous Formation[J]. Chinese Journal of Geophysics, 1996, 39 (Sup.1) : 371-378. |
| [5] | 张建华, 胡启, 刘振华. 钻井泥浆滤液侵入储集层的理论计算模型[J]. 石油学报, 1994, 15 (4) : 73-78. Zhang Jianhua, Hu Qi, Liu Zhenhua. A Theoretical Model for Mud-Filtrate Invasion in Reservoir Formations During Drilling[J]. Acta Petrolei Sinica, 1994, 15 (4) : 73-78. |
| [6] | Mark A P, Wilson C C, Mohan M, et al. Multiple Factors that Influence Wireline Formation Tester Pressure Measurements and Fluid Contacts Estimates[C]//SPE Annual Technical Conference and Exhibition. New Orleans:Society of Petroleum Engineers, 2001:1-16. |
| [7] | Won S, Bilgesu H I, Ameri S. Investigation of Mud-Filtrate Using Computational Fluid Dynamics[C]//SPE Eastern Regional/AAPG Eastern Section Joint Meeting. Pittsburgh:Society of Petroleum Engineers, 2008:1-9. |
| [8] | 徐文远.泥浆侵入数值模拟及校正方法研究[D].武汉:长江大学, 2012. Xu Wenyuan. A Study Based on Numerical Simulation for Resistivity Correction in Mud-Invasion Reservoir[D]. Wuhan:Yangtze University, 2012. |
| [9] | Mayank M, Carlos T V, Jesús M S, et al. Influence of Petrophysical and Fluid Properties on Apply-Induction Measurements Acquired in the Presence of Oil-Base Mud-Filtrate Invasion[C]//SPWLA 48th Annual Logging Symposium.[S. l.]:Society of Petrophysicists and Well-Log Analysts, 2007:1-16. |
| [10] | 常文会, 潘和平, 周峰. 泥浆侵入二维数值模拟[J]. 地球科学:中国地质大学学报, 2010, 35 (4) : 674-680. Chang Wenhui, Pan Heping, Zhou Feng. Two-Dimensional Numerical Simulation of Mud Invasion[J]. Earth Science:Journal of China University of Geosciences, 2010, 35 (4) : 674-680. DOI:10.3799/dqkx.2010.082 |
| [11] | Wu J, Carlos T V, Kamy S, et al. Numerical Simu-lation of Mud-Filtrate Invasion in Deviated Wells[J]. SPE Reservoir Evaluation & Engineering, 2004, 7 (2) : 143-154. |
| [12] | 杨震, 李志强, 邓少贵, 等. 大斜度井钻井液侵入数值模拟[J]. 中国石油大学学报(自然科学版), 2008, 32 (3) : 55-59. Yang Zhen, Li Zhiqiang, Deng Shaogui, et al. Numerical Simulation of Drilling Fluid Invasion in Highly Deviated Wells[J]. Joumal of China University of Petroleum (Edition of Natural Sciences), 2008, 32 (3) : 55-59. |
| [13] | 邓少贵, 李志强, 范宜仁, 等. 斜井泥浆侵入仿真及其阵列侧向测井响应数值模拟[J]. 地球物理学报, 2010, 53 (4) : 994-1000. Deng Shaogui, Li Zhiqiang, Fan Yiren, et al. Numerical Simulation of Mud Invasion and Array Laterolog Response in Deviaed Wells[J]. Chinese Journal of Geophysics, 2010, 53 (4) : 994-1000. |
| [14] | Dewan J T, Martin E. Mudcake Buildup and Invasion in Low Permeability Formations:Application to Permeability Determination by Measurement While Drilling[C]//SPWLA 34th Annual Logging Symposium. Calgary:Society of Petrophysicists and Well-Log Analysts, 1993:1-24. |
| [15] | 范宜仁, 胡云云, 李虎, 等. 泥饼动态生长于泥浆侵入数值模拟[J]. 测井技术, 2013, 37 (5) : 466-471. Fan Yiren, Hu Yunyun, Li Hu, et al. Numerical Simulation of Mud-Cake Dynamic Formation and Reservoir Mud Filtrate Invasion[J]. Well Logging Technology, 2013, 37 (5) : 466-471. |
| [16] | Ling K, Shen Z, He J, et al. A Comprehensive App-roach to Estimate Invasion Radius of Mud Filtrate to Evaluate Formation Damage Caused by Overbalanced Drilling[C]//SPE International Symposium and Exhibition on Formation Damage Control. Lafayette:Society of Petroleum Engineers, 2014:1-18. |
| [17] | Tobola D P, Holditch S A. Determination of Reser-voir Permeability from Repeated Induction Logging[J]. SPE Formation Evaluation, 1991, 6 (1) : 20-26. DOI:10.2118/19606-PA |
| [18] | 邓少贵, 范宜仁, 谢关宝, 等. 泥浆侵入地层双感应测井曲线正负差异特性分析[J]. 测井技术, 2004, 28 (6) : 496-498. Deng Shaogui, Fan Yiren, Xie Guanbao, et al. The Influential Factors on Electrolog Response of Formation with Mud Filtration Invasion[J]. Well Logging Technology, 2004, 28 (6) : 496-498. |
| [19] | 范文同, 章成广, 周红涛, 等. 塔河油田电阻率泥浆侵入影响分析与校正[J]. 石油天然气学报, 2009, 31 (4) : 86-90. Fan Wentong, Zhang Chengguang, Zhou Hongtao, et al. The Analysis and Correction for Effect of Mud Invasion on Resistivity in Tahe Oilfield[J]. Journal of Oil and Gas Technology, 2009, 31 (4) : 86-90. |
| [20] | 任好, 章成广, 刘晓梅. 泥浆侵入对阵列感应电阻率测井影响的数值模拟与校正[J]. 石油天然气学报(江汉石油学院学报), 2006, 28 (3) : 82-84. Ren Hao, Zhang Chengguang, Liu Xiaomei. Numerical Simulation and Correction of Influence of Array Induction Resistivity Logging in Mud Invaded Reservoirs[J]. Journal of Oil and Gas Technology (Journal of Jianghan Petroleum Institute), 2006, 28 (3) : 82-84. |
| [21] | 韩大匡. 油藏数值模拟基础[M]. 北京: 石油工业出版社, 1993 : 1-325. Han Dakuang. Reservoir Numerical Simulation[M]. Beijing: Publishing House of Oil Industry, 1993: 1-325. |
| [22] | Zhang J, Hu Q, Liu Z. Estimation of True Forma-tion Resistivity and Water Saturation with a Time-Lapse Induction Logging Method[J]. The Log Analyst, 1999, 40 (2) : 138-148. |
| [23] | 张剑波, 李谢清, 石阳, 等. 油藏数值模拟中地质模型的建模流程与方法[J]. 吉林大学学报(地球科学版), 2015, 45 (3) : 860-868. Zhang Jianbo, Li Xieqing, Shi Yang, et al. Processes and Technology of Three-Dimensional Geological Modeling System in Numerical Reservoir Simulation[J]. Journal of Jilin University (Earth Science Edition), 2015, 45 (3) : 860-868. |
| [24] | 张建华, 欧阳健. 泥浆侵入储层电阻率测井动态反演多解性研究[J]. 测井技术, 2000, 24 (2) : 102-107. Zhang Jianhua, Ouyang Jian. Study of Multi-Solution Characters for Inversion of Dynamic Resistivity Logging Responses to Oil/Gas Formation Invaded by Mud-Filtrate[J]. Well Logging Technology, 2000, 24 (2) : 102-107. |
| [25] | 朱留芳, 沈建国. 测井曲线几何因子理论[J]. 测井技术, 2013, 37 (6) : 624-628. Zhu Liufang, Shen Jianguo. The Geometric Factor Theory for Logging Curves[J]. Well Logging Technology, 2013, 37 (6) : 624-628. |


