0 引言
偏移成像是用于探测地下地质结构、指导油气勘探和生产的重要处理技术,由于观测系统孔径、复杂的上覆构造及目标倾角等因素的影响,常常产生扭曲的地下成像结果。地震照明分析对上述影响因素提供了有效的定量分析,是复杂构造及区域地震采集设计的有效手段。常见的地震照明分析方法主要分为两大类:基于射线理论的射线照明分析[1]和基于波动理论的波动方程照明分析[1-5]。基于射线的地震波照明分析方法能够适应非规则的观测系统及横向速度变化模型,且没有角度限制,因此广泛应用于照明计算中[6-7]。但是高频渐进特性和射线理论本身的缺陷,使得该技术很难适用于具有复杂上覆结构的目标区。单程波传播算子广泛地应用于地震偏移成像中,同时由地震波场中抽取角度信息的技术获得了发展[8-9]。研究者提出了基于单程波波动方程的照明分析方法[10-15],但是该方法不能正确处理诸如回转波等大角度波场。基于双程波波动方程的逆时偏移成像(reverse time migration, RTM)由于没有角度限制并能对陡倾角构造正确成像而重新引起了人们的注意。Xie等[16]提出了结合双程波有限差分传播算子及时域局部慢度分析的波场角度及照明计算方法;Cao等[17]提出了频域裂步局部平面波分解的波场角度分析方法并应用于照明计算;Xie等[18-19]、Wu等[20]、Mao等[21]研究了成像分辨率函数、点弥散函数(point spreading function, PSF)及波数域照明之间的关系;Jin等[22]进行了基于照明的地震可视性分析并应用于叠前成像校正;李万万[23]通过照明及分辨率分析研究了面向对象的地震观测系统的优化设计;Li等[24]研究了基于照明分析的采集系统优化设计;朱金平等[25]研究了对地下给定目标进行照明时对地表观测系统的要求。
由于需要在模型局部空间进行波场传播角度的分解,因此采用局部平面波分解等方法均需要大量的计算。Hu等[26]对波场传播方向提取方法进行了详细的总结。第一类是基于方向矢量的方法,例如Poynting矢量[27]、极化矢量或瞬时波数矢量[28-29]等。这类方法计算效率高,具有较好的角度分辨率。缺点是在每个空间点的每个时间步长上只能得到一个传播方向,对于有多个波同时到达的情况,存在一定问题。第二类方法是在成像阶段进行局部空间偏移或时间移位成像,获得偏移距域共成像点道集,然后通过傅里叶变换或Radon变换转换到角度域[30-34]。该方法计算量较大,且只能在成像过程中进行角度分解。第三类方法是局部平面波分解,通过倾斜叠加[8, 35]、子波变换[11]或局部傅里叶变换[36-37]对源及接收波场进行局部平面波分解。这种方法的角度分解独立于成像过程,计算比较稳定,但是仍需要大量的计算。当同时存在多个波前时,利用Poynting矢量不能分别提取每个波场传播角度,但是由于其计算效率高、角度分辨率好等优点,在角度域偏移成像及相关分析中仍获得了广泛的应用。裴正林[38]从地震波能量理论出发, 提出了基于Poynting矢量的地震波场方向性分解方法和地震波定向照明度计算方法,计算精度高且速度快, 具有一定的实用性。雷涛等[39]采用双程声波波动方程传播算子,通过地震波传播的Poynting矢量分析对波场进行方向性分解,进而提出了一种面向目标区的地震定向照明分析技术。
本文给出了一种基于Poynting矢量的地震定向照明分析及成像补偿方法。采用一阶速度-应力方程及交错网格计算双程声波波场,同时计算源及接收波场的Poynting矢量并进行波场角度分解。由角度域波场计算不同入射及散射角下的部分照明,据此建立局部照明矩阵。该矩阵可以作为角度域照明分析的基础,包括了在目标附近所有可能的入射和散射方向对照明的贡献,通过研究入射和反射波在角度域中与反射面的相互作用,获得对地下结构的不同照明描述及采集倾角响应[40]。文中以SEG/EAGE模型作为数值计算实例,进行基于Poynting矢量的照明分析及成像补偿。
1 波场方向性分解Yoon等[41]利用Poynting矢量提取震源及检点波场的角度信息,并据此构建了角度域成像条件。二维声波波动方程的Poynting矢量P可以通过下式计算:
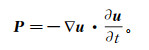 (1)
(1) 其中:u为波场;∂u/∂t为波场的时间微分;▽u=(∂u/∂x, ∂u/∂z)为波场的空间梯度。式(1)需要计算波场的时间和空间导数,计算较复杂。为便于计算Poynting矢量,采用一阶应力-速度波动方程构建波场传播算子:
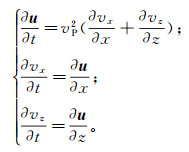 (2)
(2) 式中:vP为介质纵波波速;vx及vz分别为x轴和z轴上的质点振动速度。对式(2)采用交错网格差分格式计算,此时Poynting矢量[42]为
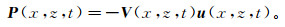 (3)
(3) 式中:P(x, z, t)为Poynting矢量;V=(vx, vz, t)为位移速度矢量。波场u及位移速度矢量在交错网格计算中可以直接得到。
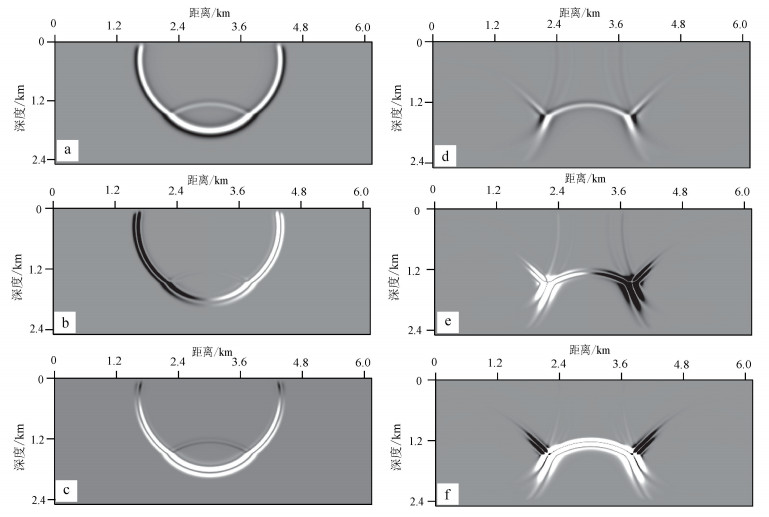
图 1为一个两层模型在t=1 s时刻的波场快照及根据式(3)计算的源及接收波场的Poynting矢量。由图 1的分解结果可以看出,通过计算Poynting矢量的各个分量值,可确定波场传播方向θ为
 (4)
(4)
|
|
图中白颜色表示正方向,黑颜色表示负方向。 a-c依次为源波场及其Poynting矢量的水平和垂直分量;d-f依次为接收波场及其Poynting矢量的水平和垂直分量。 图 1 源和接收波场快照及Poynting矢量 Figure 1 Snapshots of source and receiver wave-fields and their Poynting vectors |
|
|
式中,px、pz分别为Poynting矢量的x及z分量。
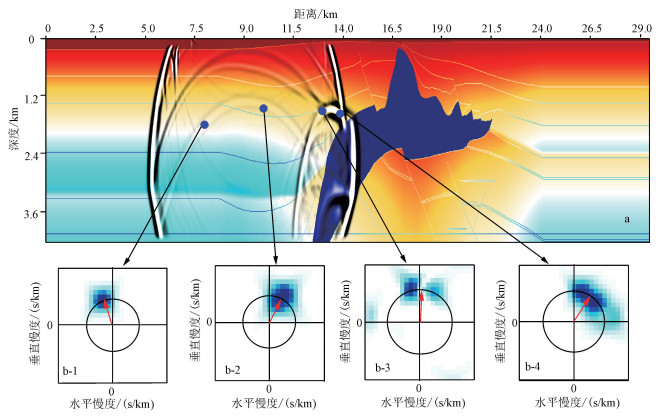
图 2为利用SEG/EAGE模型采用慢度分析[16, 38]及Poynting矢量方法计算波场传播方向的结果。图 2a是SEG/EAGE速度模型,单个震源发出的波场快照叠加在速度模型上面。图 2b是在波前若干位置处进行慢度分析及Poynting矢量计算的角度分解结果:频散关系导致慢度分析中不同的能量峰落在不同半径的圆上,峰的大小给出波的能量,其在极坐标中的方位给出了波的传播方向[40];红色箭头为利用Poynting矢量得到的波传播方向。在只有单个波前的情况下,两种方法得到的传播方向基本相同(图 2b-1、b-2);但是当有多个波前时,慢度分析可以给出每个波前的传播方向,Poynting矢量只能给出一个传播方向的估计(图 2b-3、b-4)。因此,Poynting矢量方法在每个时刻每个网格点上只能得到一个传播方向。为了提高Poynting矢量方法计算传播方向的稳定性,人们提出了空间域或时间域Poynting矢量平滑滤波等不同的处理技术[43-45]。尽管Poynting矢量方法存在一定的缺陷,但是由于其大大降低了角度估计的计算量,仍获得了广泛的应用。
|
| 图 2 慢度分析及Poynting矢量计算的波场传播方向 Figure 2 Direction of wavefield by slowness analysis and Poynting vector respectively |
|
|
根据前述波场分解过程,可以将源及接收波场分解为沿入射角θs及散射角θg方向的不同波束,照明分析可以从研究目标处的θs角度入射波束和θg角度散射波束开始。入射-散射波束构成了最基本的照明测量。由于多径、散射及反射等,由震源到目标处的波可能来自多个方向,由目标到检波器的过程类似。收集来自一对震源-检波器的所有可能的入射-散射波束即可给出目标照明的完整描述。给定一对震源及检波器,在频域内,目标的局部照明矩阵[4]可表示为
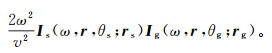 (5)
(5) 式中:ω为频率;v为局部速度;r为目标位置;rs及rg分别为震源及检波器位置;Is及Ig分别为源波场沿θs方向及检点波场沿θg方向的能量流。且有
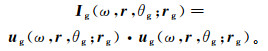 (7)
(7) 式中,us(ω, r, θs; rs)及ug(ω, r, θg; rg)分别为源及检点波场θs及θg方向的角度域分量。根据时域与频域之间的对应关系,有:
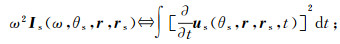 (8)
(8) 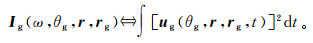 (9)
(9) 由此可得时域内局部照明矩阵为
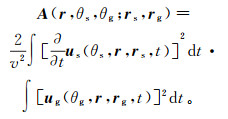 (10)
(10) 式中:A为局部照明矩阵;us(θs, r, rs, t)与ug(θg, r, rg, t)分别为r处t时刻的源及接收波场θs及θg方向的分量。θs及θg分别由下式确定:
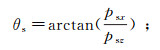 (11)
(11) 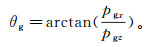 (12)
(12) 式中,psx与psz、pgx与pgz分别为源及接收波场在r处t时刻x及z方向的Poynting矢量分量。若采集系统包含多个震源及检波器,其局部照明矩阵可由每对源-检点对的照明累加得到:
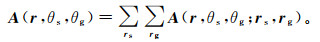 (13)
(13) 其中,(rs, rg)的空间位置与所设计的采集系统有关。局部照明矩阵A是空间位置r的函数。照明矩阵包含了目标处所有入射和散射角度情况下的照明情况,通过研究局部照明矩阵A可以方便地分析采集系统对目标r的照明作用[40]。
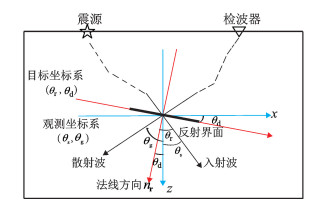
利用坐标转换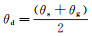
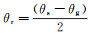
|
| 图 3 观测坐标系(蓝色)与目标坐标系(红色) Figure 3 Observation coordinate (blue) and target coordinate (red) |
|
|
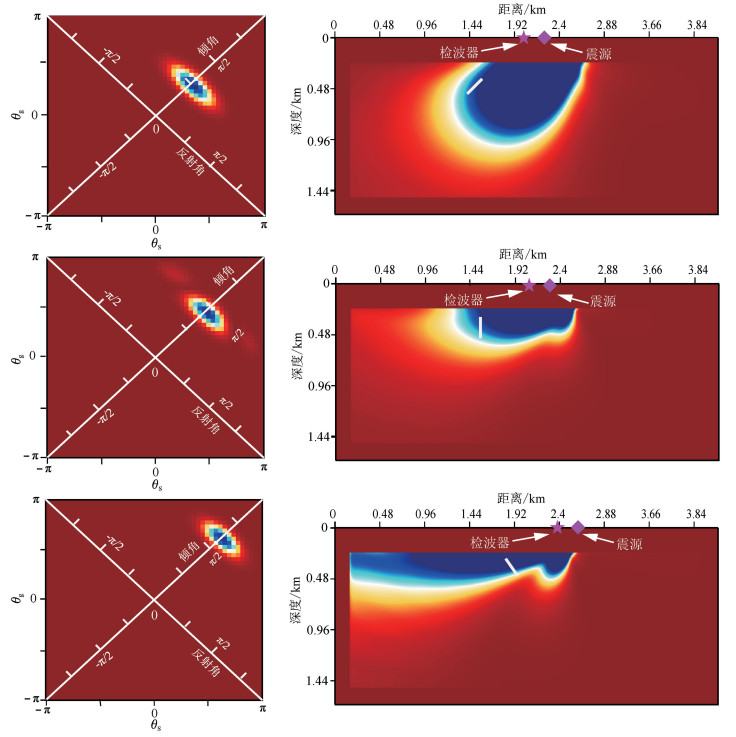
|
| 自上而下依次为反射界面倾角为45°、90°、120°时的局部照明矩阵。 图 4 局部照明矩阵 Figure 4 Localillumination matrix |
|
|
局部照明矩阵包含了局部目标处所有方向的入射波和散射波及局部界面倾角信息,因此在局部照明矩阵中可以进行各种不同类型的照明分析。采集倾角响应(acquisition dip response, ADR)是震源-检波器对关于具有特定倾角的目标的总照明,描述了对地下特定倾角界面的探测能力。如果已估计出模型中局部反射界面的倾角,则可以在局部照明矩阵中计算其对应的采集倾角响应:
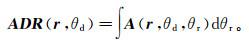 (14)
(14) 理想情况下,RTM成像的幅度直接与反射系数相关;但实际上,由于有限的采集孔径导致的不均衡照明、复杂上覆构造及反射界面倾角等诸多因素的影响,RTM像的真实幅度产生扭曲。ADR可以用于RTM成像校正,以提高成像质量。校正后的像为
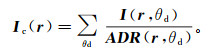 (15)
(15) 式中:Ic(r)为位置r处校正后的像;I(r, θd)为共倾角部分的像。
3 数值计算本文选用标准的SEG/EAGE二维盐丘模型(图 5)作数值试验。该模型是根据墨西哥湾的实际地质构造而产生的, 模型中不仅含有高速盐体, 还有陡倾构造。网格点数为1 200×300,水平及垂直网格间距均为12.192 m。合成数据采用右侧放炮、左侧接收的单边采集方式,共计301炮,炮间距48.768 m,每炮161个检波器,检波器间距12.192 m,震源函数为15 Hz的Ricker子波。图 5为在SEG/EAGE盐丘模型中选择了8个位置(如图中圆点所示)计算的局部照明矩阵。由图 5可以看出,由于单边接收,照明范围主要集中在矩阵右下部的三角形区域。对于单程波方程,入射角和散射角范围为±90°,因此其照明角度区域限于图 5中虚线所示范围。由于采用双程波波动方程计算波场,入射角和散射角可达到±180°的照明计算范围,可以实现陡倾角等复杂界面的照明分析,对于实现逆时偏移的照明补偿及成像校正具有重要意义。随着深度的增加,反射角覆盖范围及可照明的倾角范围也随之减小。高速盐体速度与背景速度存在显著差异,导致盐体附近部位的局部照明矩阵形态相对复杂。由于高速盐体对波的剧烈衰减作用,盐体下部的照明明显不足,因此对高速盐体下部区域的成像困难[40]。
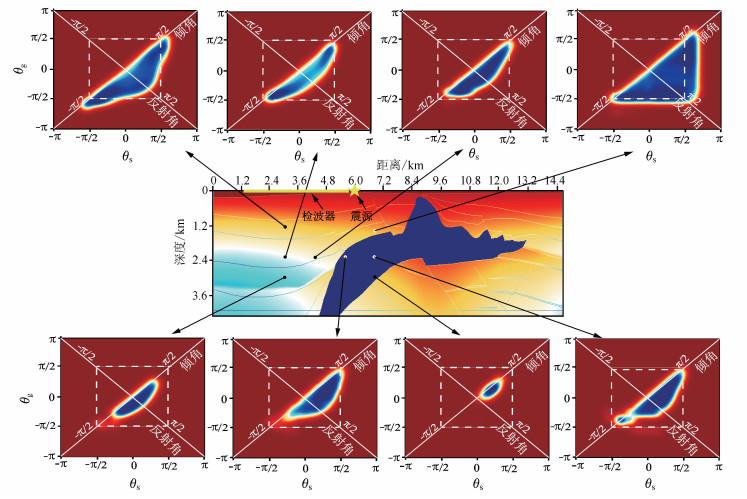
|
| 图 5 SEG/EAGE模型中不同位置的局部照明矩阵 Figure 5 Local illumination matrix for different positions in SEG/EAGE model |
|
|
图 6为SEG/EAGE模型在不同地下构造倾角方向和全角度的照明结果。采用中间放炮、两侧接收的双边采集方式,每炮161个检波器,其他参数与上述相同。某个倾角方向的照明强度的强弱,反映了观测系统是否能有效地获取该倾角方向构造的反射信息。如果照明强,则在这些倾角方向构造上偏移成像的效果就好。由图 6可以看出,尽管在0°倾角时盐体下的照明分布相对均匀,但是其他倾角时的照明分布差异很大,尤其对于大角度情况。因此,在上述观测系统下,照明强度总体较弱,-30°和-45°倾角方向的照明能力更差,在这些倾角方向构造的反射信息难以获取,成像效果较差。
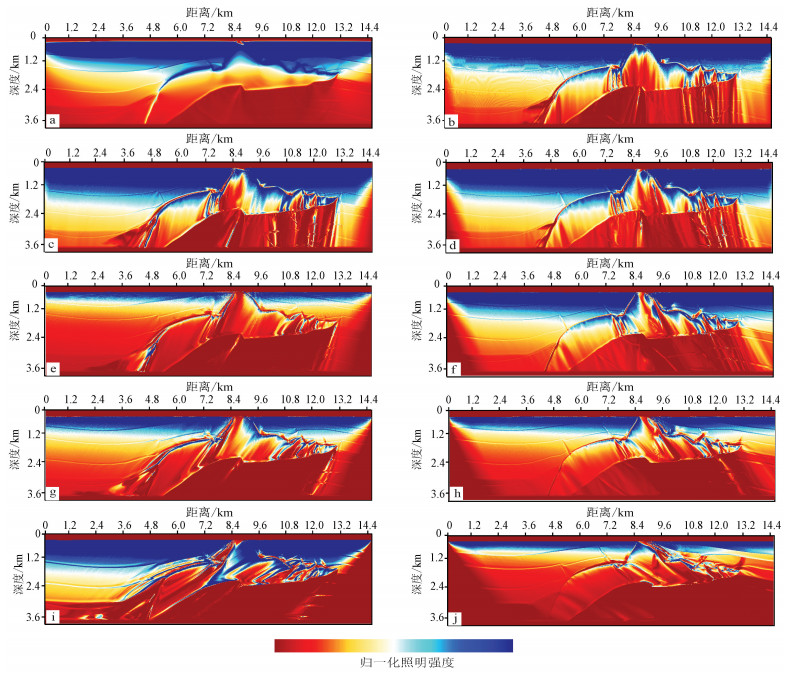
|
| a.全角度照明;bj.倾角依次为0°、-15°、15°、-30°、30°、-45°、45°、-60°、60°时的采集倾角响应。 图 6 SEG/EAGE模型不同倾角的的采集倾角响应 Figure 6 Acquisition dip response for different dip angle in SEG/EAGE model |
|
|
图 7是利用式(15)将ADR用于RTM成像校正的结果。从图 7可以看到,经ADR校正后的像不但增强了构造成像效果,并且降低了成像噪声。

|
| a.未校正的RTM像;b.校正后的像;c、d. a中白色区域校正前后的像。 图 7 SEG/EAGE成像及采集倾角响应校正后的像 Figure 7 Regular RTM image of SEG/EAGE model and the imagecorrected by acquisition dip response |
|
|
1) 本文讨论了基于Poynting矢量方法的波场角度分解和照明分析,并以此为基础构造了局部照明矩阵。该矩阵是分析波场与反射体相互作用及定向照明分析的有效工具。
2) 根据局部照明矩阵进行采集倾角响应计算,并将其应用于RTM成像校正。
3) 为验证所述方法,利用SEG/EAGE二维模型进行了数值计算,实验结果表明了方法的有效性。
4) 相比于其他的波场角度分解方法,基于Poynting矢量的方法具有更高的计算效率。但是该方法在每个时空点只能确定一个传播方向,所以对于有多个波场同时到达的情况其计算的传播角度可能存在误差,需要在实际应用折中考虑。
致谢: University of California-Santa Cruz MIL研究组的陈波、严哲等在照明分析中提供的有益帮助,在此表示感谢。| [1] | Gelius L J, Lecomte I, Tabti H. Analysis of the Resolution Function in Seismic Prestack Depth Imaging[J]. Geophysical Prospecting, 2002, 50 (5) : 505-515. DOI:10.1046/j.1365-2478.2002.00331.x |
| [2] | Lecomte I. Resolution and Illumination Analyses in PSDM:A Ray-Based Approach[J]. The Leading Edge, 2008, 27 (5) : 650-663. DOI:10.1190/1.2919584 |
| [3] | Xie X B, Wu R S, Fehler M, et al. Seismic Resolution and Illumination:A Wave Equation Based Analysis[C]//Expanded Abstracts of the 75th Annual International Meeting. Houston:SEG, 2005:1862-1865. |
| [4] | Xie X B, Jin S W, Wu R S. Wave-Equation Based Seismic Illumination Analysis[J]. Geophysics, 2006, 71 (5) : S169-S177. DOI:10.1190/1.2227619 |
| [5] | Wu R S, Chen L. Directional Illumination Analysis Using Beamlet Decomposition and Propagation[J]. Geophysics, 2006, 71 (4) : S147-S159. DOI:10.1190/1.2204963 |
| [6] | Schneider W A, Winbow G A. Efficient and Accurate Modeling of 3-D Seismic Illumination[C]//Expanded Abstracts of the 69th Annual International Meeting. Houston:SEG,1999:633-636. |
| [7] | Muerdter D, Ratcliff D. Understanding Subsalt Illumi-nation Through Ray-Trace Modeling:Part 1:Simple 2-D Salt Models[J]. The Leading Edge, 2001, 20 (6) : 578-594. DOI:10.1190/1.1438998 |
| [8] | Xie X B, Wu R S. Extracting Angle Domain Infor-mation from Migrated Wavefields[C]//Expanded Abstracts of the 72th Annual International Meeting. Salt Lake City:SEG, 2002:1360-1363. |
| [9] | Sava P, Fomel S. Angle-Domain Common Image Ga-thers By Wavefield Continuation Methods[J]. Geophysics, 2003, 68 (3) : 1065-1074. DOI:10.1190/1.1581078 |
| [10] | Xie X B, Jin S W, Wu R S. Three-Dimensional Illu-mination Analysis Using Wave-Equation Based Propagator[C]//Expanded Abstracts of the 73rd Annual International Meeting. Dallas:SEG, 2003:989-992. |
| [11] | Wu R S, Chen L. Mapping Directional Illumination and Acquisition-Aperture Efficacy by Beamlet Propagators[C]//Expanded Abstracts of the 72nd Annual International Meeting. Salt Lake City:SEG, 2002:1352-1355. |
| [12] | Wu R S, Chen L, Xie X B. Directional Illumination and Acquisition Dip-Response[C]//Expanded abstracts of the 65th Conference and Technical Exhibition. Stavanger:EAGE, 2003(Z-99):1-4. |
| [13] | Jin S W, Walraven D. Wave Equation GSP Prestack Depth Migration and Illumination[J]. The Leading Edge, 2003, 22 (7) : 606-610. DOI:10.1190/1.1599687 |
| [14] | Jin S W, Luo M Q, Xu S, et al. Illumination Amp-litude Correction with Beamlet Migration[J]. The Leading Edge, 2006, 25 (9) : 1046-1050. DOI:10.1190/1.2349807 |
| [15] | Mao J, Wu R S. Illumination Analysis Using Local Exponential Beamlets[C]//Expanded Abstracts of the 77th Annual International Meeting. San Antonio:SEG, 2007:2235-2239. |
| [16] | Xie X B, Yang H. A Full-Wave Equation Based Seismic Illumination Analysis Methods[C]//Extended Abstracts of the 70th Annual International Conference and Exhibition. Rome:EAGE, 2008:284. |
| [17] | Cao J, Wu R S. Local-Angle Domain Illumination for Full-Wave Propagators[C]//Expanded Abstracts of the 78th Annual International Meeting. Las Vegas:SEG, 2008:2246-2251. |
| [18] | Xie X B, Wu R S, Fehler M, el al. Seismic Reso-lution and Illumination:A Wave Equation Based Analysis[C]//Expanded Abstracts of the 75th Annual International Meeting. Houston:SEG, 2005:1862-1865. |
| [19] | Xie X B, Jin S W, Wu R S. Wave-Equation Based Seismic Illumination Analysis[J]. Geophysics, 2005, 71 (5) : S169-S177. |
| [20] | Wu R S, Xie X B, Fehler M, el at. Resolution Analysis of Seismic Imaging[C]//Extended Abstracts of the 68th Annual International Conference and Exhibition. Wien:EAGE, 2006:G048. |
| [21] | Mao J, Wu R S. Fast Image Decomposition in Dip Angle Domain and Its Application for Illumination Compensation[C]//Expanded Abstracts of the 81th Annual International Meeting. San Antonio:SEG, 2011:3201-3204. |
| [22] | Jin S W, Xu S. Seismic Visibility Analysis and Its Applications to Data Acquisition and Prestack Migration[C]//Extended Abstract of the 71th EAGE Annual Conference. Amsterdam:EAGE, 2009:SO15. |
| [23] | 李万万. 基于波动方程正演的地震观测系统设计[J]. 石油地球物理勘探, 2008, 43 (2) : 134-141. Li Wanwan. Design of Seismic Geometry Based on Wave Equation Forward Simulation[J]. Oil Geophysical Prospecting, 2008, 43 (2) : 134-141. |
| [24] | Li P M, Dong L G. Optimal Seismic Survey Design Based on Seismic Wave Illumination[C]//Extended Abstracts of the 68th Annual International Conference and Exhibition. Wien:EAGE, 2006:FO29. |
| [25] | 朱金平, 董良国, 程玖兵. 基于地震照明、面向勘探目标的三维观测系统优化设计[J]. 石油地球物理勘探, 2011, 46 (3) : 339-348. Zhu Jinping, Dong Liangguo, Cheng Jiubing. Target-Oriented 3D Seismic Optimal Geometry Design Based on Seismic Illumination[J]. Oil Geophysical Prospecting, 2011, 46 (3) : 339-348. |
| [26] | Hu J, McMechan G A, Guan H M. Comparison of Methods for Extracting ADCIGs from RTM[J]. Geophysics, 2014, 79 (3) : 89-103. DOI:10.1190/geo2013-0336.1 |
| [27] | Yoon K, Kurt J, Marfurt J K. Reverse-Time Migra-tion Using the Poynting Vector[J]. Exploration Geophysics, 2006, 37 (1) : 102-107. DOI:10.1071/EG06102 |
| [28] | Zhang Q S, McMechan G A. Common-Image Gathers in the Incident Phase-Angle Domain from Reverse Time Migration in 2D Elastic VTI Media[J]. Geophysics, 2011, 76 (6) : 197-206. DOI:10.1190/geo2011-0015.1 |
| [29] | Zhang Q S, McMechan G A. Direct Vector-Field Method to Obtain Angle-Domain Common-Image Gathers from Isotropic Acoustic and Elastic Reverse-Time Migration[J]. Geophysics, 2011, 76 (5) : 135-149. |
| [30] | Sava P, Fomel S. Angle-Domain Common Image Gathers by Wavefield Continuation Methods[J]. Geophysics, 2003, 68 (3) : 1065-1074. DOI:10.1190/1.1581078 |
| [31] | Sava P, Fomel S. Coordinate-Independent Angle Gathers for Wave Equation Migration[C]//Expanded Abstracts of the 75th Annual International Meeting. Houston:SEG, 2005:2052-2055. |
| [32] | Sava P, Fomel S. Time-Shift Imaging Condition[C]//Expanded Abstracts of the 75th Annual International Meeting. Houston:SEG, 2005:1850-1853. |
| [33] | Sava P, Fomel S. Wave-Equation Common Angle Gathers for Converted Waves[C]//Expanded Abstracts of the 75th Annual International Meeting. Houston:SEG, 2005:947-950. |
| [34] | Sava P, Vasconcelos I. Extended Imaging Conditions for Wave Equation Migration[J]. Geophysical Prospecting, 2011, 59 (1) : 35-55. DOI:10.1111/gpr.2010.59.issue-1 |
| [35] | Yan R, Xie X B. An Angle-Domain Iimaging Condi-tion for Elastic Reverse Time Migration and Its Application to Angle Gather Extraction[J]. Geophysics, 2012, 77 (5) : 105-115. DOI:10.1190/geo2011-0455.1 |
| [36] | 高成, 孙建国. 不同域的局部平面波分解应用与对比[J]. 吉林大学学报(地球科学版), 2015, 45 (5) : 1523-1529. Gao Cheng, Sun Jiguo. Local Plane Wave Decomposition Methods in Different Domain[J]. Journal of Jilin University (Earth Science Edition), 2015, 45 (5) : 1523-1529. |
| [37] | Xu S, Zhang Y, Tang B. 3D Common Image Gathers from Reverse Time Migration[J]. Geophysics, 2011, 76 (2) : S77-S92. DOI:10.1190/1.3536527 |
| [38] | 裴正林. 波动方程地震定向照明分析[J]. 石油地球物理勘探, 2008, 43 (6) : 645-651. Pei Zhenglin. Analysis on Wave Equation Seismic Directional Illumination[J]. Oil Geophysical Prospecting, 2008, 43 (6) : 645-651. |
| [39] | 雷涛, 顾汉明, 李列, 等. 面向目标靶区的双程波动方程地震定向照明分析[J]. 石油物探, 2014, 53 (4) : 437-443. Lei Tao, Gu Hanming, Li Lie, et al. Target-Oriented Seismic Directional Illumination Analysis Based on Two-Way Acoustic Wave Equation[J]. Geophysical Prospecting for petroleum, 2014, 53 (4) : 437-443. |
| [40] | 谢小碧, 何永清, 李培明. 地震照明分析及其在地震采集设计中的应用[J]. 地球物理学报, 2013, 56 (5) : 1-14. Xie Xiaobi, He Yongqing, Li Peiming. Seismic Illumination Analysis and Its Applications in Seismic Survey Design[J]. Chinese Journal of Geophysics, 2013, 56 (5) : 1-14. |
| [41] | Yoon K, Marfurt, Starr W. Challenges in Reverse-Time Migration[C]//Expanded Abstracts of the 74th Annual International Meeting. Denver:SEG, 2004:1057-1060. |
| [42] | 王保利, 高静怀, 陈文超, 等. 逆时偏移中用Poynting矢量高效地提取角道集[J]. 地球物理学报, 2013, 56 (1) : 262-268. Wang Baoli, Gao Jinghuai, Chen Wenchao, et al. Extracting Efficiently Angle Gathers Using Poynting Vector During Reverse Time Migration[J]. Chinese Journal of Geophysics, 2013, 56 (1) : 262-268. |
| [43] | Yoon K, Guo M H, Cai J, et al. 3D RTM Angle Gathers from Source Wave Propagation Direction and Dip of Reflector[C]//Expanded Abstracts of the 81th Annual International Meeting. San Antonio:SEG, 2011:3136-3140. |
| [44] | Yan J, Ross W. Improving the Stability of Angle Gather Computation Using Poynting Vectors[C]//Expanded Abstracts of the 83th Annual International Meeting. Houston:SEG, 2013:3784-3788. |
| [45] | Dickens A, Winbow G A. RTM Angle Gathers Using Poynting Vectors[C]//Expanded Abstracts of the 81st Annual International Meeting. San Antonio:SEG, 2011:3109-3113. |



