0 引言
裂缝是地壳中最常见的结构特征,裂缝型油气藏泛指以裂缝及孔隙为油气储集空间的储层。研究表明,以碳酸盐岩和非常规油气(致密气和页岩气)为主的绝大多数储层都包含天然裂缝结构[1-2],其储量超过世界探明油气总量的一半。甚至有学者提出:“在有明确证据排除之前,所有储层都应该被当做裂缝性对待。”[3]裂缝既可以作为流体的储集空间,又能成为流体的渗流通道,对储层管理和经济评价均有深远影响;因此,对裂缝更有效、更精细的描述逐渐成为勘探地球物理学追寻的目标。
目前,裂缝检测和描述方法大致可分为钻井测井手段和地震手段两种。钻井取心和测井手段有可信度高和精度高的优点;但裂缝描述结果的有效性只能局限在特定井位或周围极小的范围内,而高昂的勘探成本也决定了该类方法无法达到较大的覆盖范围。相比之下,地震手段的空间覆盖范围较大,有利于对裂缝储层的分布情况和岩石物理特征做出总体描述[4-5]。特别是近30年来,AVO (amplitude variation with offset)反演技术的快速发展为利用地震手段描述裂缝储层提供了新的思路。如Ruger等[6]通过解析裂缝储层AVO响应,阐述了与纵波反射系数有关的裂缝信息,并给出了在弱各向异性假设下HTI (horizontal transverse isotropy)介质中的纵波近似反射系数公式。刘财等[7]提出了一种基于方位相交的纵波AVO数据反演储层裂缝密度方法。
然而,由于裂缝性储层有成因复杂、裂缝多尺度、填充物多类型和分布非均匀等特点,以往的数据驱动类AVO反演方法往往不能取得较好的效果。为了克服这些难点,近年来涌现出一类基于等效介质理论的模型驱动类AVO反演方法;该类方法直接从裂缝储层的宏观或者微观特征入手,通过匹配地震响应来反演模型参数,得到的参数具有明确的岩石物理意义。典型的有:刘喜武等[8]提出了一种基于Chapman模型的裂缝渗透率反演策略;桂金咏等[9]基于Gassmann理论提出了一种孔隙度、含气饱和度和泥质含量的反演方法;Guo等[10]基于Carcione薄互层模型提出了一种储层孔隙度及层厚度同步反演方法。在此基础上,兰慧田[11]进一步探讨了薄层裂缝储层中的参数反演问题。
基于等效介质理论的裂缝描述方法中一个关键任务就是根据实际问题选择合适的等效介质模型。与裂缝储层相关的等效介质模型可以分为静态和动态两类。静态等效介质模型的假设是频率和尺度独立,反映裂缝在长波长极限条件下的地震响应,无法量化裂缝几何结构和微观细节信息(如裂缝尺寸、裂缝密度、流体类型等),也无法模拟裂缝储层引起的地震波频散衰减现象。如Hudson的孤立裂缝模型[12]、Schoenberg的线性滑动模型[13]、Thomson的等径孔隙模型[14]等。而事实上,这些频散和衰减响应是很重要的,研究地震各向异性的频率依赖特性可以为我们提供更加丰富的储层信息;因此,动态等效介质模型的引入具有很强的现实意义。该类模型在考虑了微观孔隙结构和流体填充的基础上,进一步兼顾了地震波传播过程中流体在孔隙和各尺度裂缝之间的交换,更加有利于我们利用地震波场进行裂缝储层描述。Parra模型[15]和BISQ模型[16]都是典型的动态裂缝等效介质模型。遗憾的是,这些模型往往更适用于超声波频段的频散预测,而对地震频段的频散现象严重低估。
基于喷射流机制,Chapman等[17]将介质假设为含有球状孔隙加随机方向扁椭球状裂隙的各向同性岩石,根据由地震波传播引起的、介质内部的、使相邻区域发生流体交换的压力梯度弛豫时间建立了新的模型,并将弹性张量整合成Eshelby[18]提出的形式,计算各频率的速度和衰减因子。随后Chapman等[19]又将该理论扩展到多尺度范围,形成一个尺度依赖、频率依赖的定量模型。后来,Liu等[20]、Maultzsch等[21]和Tillotson等[22]陆续通过实际数据观测和解释验证了这一模型的有效性。在此基础上,Chapman等[23]又利用数值方法研究了高频散储层在反射地震资料中的影响,发现反射界面的频率响应与AVO表现关系密切。也就是说,我们可以凭借Chapman模型为实际观测地震资料中的振幅频变异常现象做出合理的建模和解释。
本文利用动态裂缝等效介质模型作为地震波频散的预测算子,借助频变AVO理论构建新的反演目标函数,实现对裂缝参数的准确估计。
1 理论与方法 1.1 裂缝等效介质模型Chapman等[17]基于喷流机制提出了一个微结构动态多孔弹性模型。该模型的固相为线性弹性固体,孔隙空间由随机分布的纵横比较小的厘米级颗粒尺度裂隙和孔隙组成。地震波的传播引起岩石中孔隙与裂隙之间、裂隙与裂隙之间的流体交换。随后,Chapman等[19]又将模型扩展至包含米级开放裂缝的中尺度, 每条裂缝可以与多个裂隙或孔隙连通,但每条裂隙、每个孔隙至多与一条裂缝连通,裂缝之间互不连通[19]。该模型通过各尺度裂缝之间的流体交换来模拟动态流体替换过程。模型的预测结果在低频范围内与Brown等[24]的结果一致,在高频范围内与Hudson孤立裂缝模型一致。通过这样一个模型,我们便可以利用岩石骨架性质(孔隙度、渗透率、裂缝密度)和孔隙流体性质(黏滞度、体积模量和密度等)模拟裂缝储层的地震波频变各向异性响应。
Chapman弹性张量的分解形式如下:
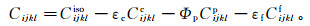 (1)
(1) 式中:Φp为孔隙度;εc为裂隙密度;εf为裂缝密度;Cijkliso为不含填充物的各向同性岩石骨架的弹性张量;Cijklc、Cijklp和Cijklf分别表示由裂隙、孔隙和裂缝引起的改变,均为拉梅系数、流体和裂缝性质以及频率的函数。
颗粒尺度(厘米级的裂纹或裂隙)和裂缝尺度(米级的裂缝)下的流体流动性对应了不同的时间尺度因子。在颗粒尺度下,流体的流动与时间尺度因子τm有关:
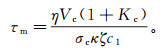 (2)
(2) 式中:η为流体的黏滞系数;Vc是单一裂隙的体积;Kc=σc/kF,kF为流体体积模量,σc为临界应力,σc=πμr/2(1-ν),r为裂缝纵横比,μ为剪切模量,ν为泊松比;κ为渗透率;ζ为颗粒尺寸;c1是孔隙空间连通点数目。而在裂缝尺度下,流体压力松弛需要更大的时间尺度因子τf:
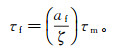 (3)
(3) 式中:af为裂隙半径。
为了使模型更加贴近实际数据,Chapman等[17]从岩石基质的密度ρ以及纵横波速度vP0、vS0入手,引入了基质拉梅系数λ0和μ0,并且进一步定义了各向同性刚度张量Ciso(Λ, M)。这样就便于在实验室中对拉梅系数做直接测量以完成模型的参数化。即,我们可以获取如下参考常数:
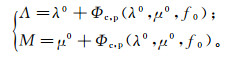 (4)
(4) 式中:Φc, p为对弹性张量的修正,它正比于εc和Φp;λ0=ρ(vP0)2-2μ0;μ0=ρ(vS0)2。那么方程(1)可以改写为
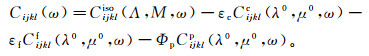 (5)
(5) 式中:ω为角频率。
通过将修正项改造成这种形式,Chapman模型保证了我们可以通过测量岩石样本来量化由裂缝、孔隙和裂隙造成的介质频变特征与各向异性[19]。研究表明,当介质不含裂隙或研究频段低于微观喷射流动频率时,可以通过忽略式(5)中与裂隙有关项来完成方程的进一步简化。
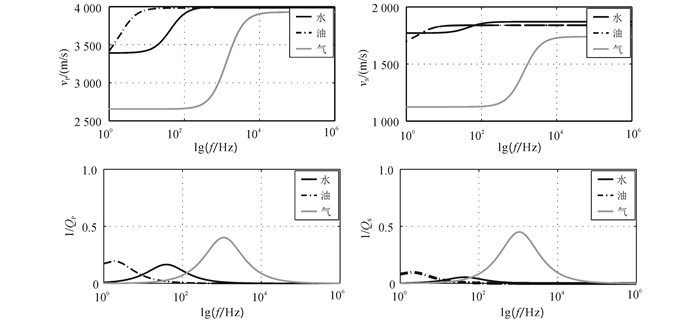
根据Chapman模型计算的随频率变化的弹性张量,任意TTI (tilted transverse isotropy)介质的弹性张量可以通过Bond转换求取,进而通过Christoffel方程预测地震波的速度频散。值得注意的是,在Chapman模型中,裂缝密度εf和时间尺度因子τf是地震波频散的两个关键输入参数,它们分别决定了频散的剧烈程度和频散发生的频带范围[23]。图 1为3种不同流体填充垂直裂缝系统时,模型计算的沿垂直裂缝传播的地震波速度和逆品质因子。图 2为3种裂缝密度情况下的模型计算结果。
|
| f为观测频率;QP、QS分别为纵、横波品质因子。 图 1 不同裂缝流体填充情况下的纵横波速度及逆品质因子 Figure 1 Predicted result for a fractured reservoir saturated with different fluid types |
|
|
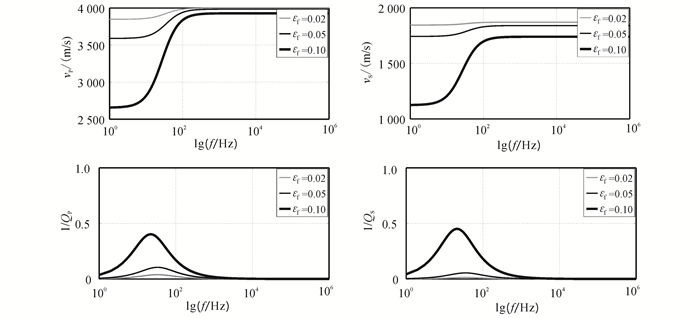
从图 1可以观察到,模型描述的频散机制包含三部分:不发生衰减的低频段、不发生衰减的高频段,以及发生显著频散和衰减现象的过度频段。在过度频段,地震波频散出现的频带范围取决于裂缝填充流体的流动性,流动性弱的流体需要更大的时间尺度因子来达到新的压力平衡状态(公式(2)),所以频散主要发生在低频段。从图 2可以观察到,频散和衰减的剧烈程度随着裂缝密度的增大而增大。这是因为,裂缝密度代表了裂缝的发育程度,地震波传播过程中较大的裂缝密度值会带来更多的流体交换量。
|
| 图 2 不同裂缝密度情况下的纵横波速度及逆品质因子 Figure 2 Predicted result for a fractured reservoir with different fracture densities |
|
|
当界面两侧介质不符合弹性、各向同性岩石的假设时,Zoeppritz方程便不再适用。Schoenberg等[25]考虑到波在界面处的应力、位移连续性,以Zoeppritz方程系数矩阵子矩阵的形式,给出了平面波反射和透射问题的显式解。该矩阵可以计算界面两侧存在非弹性或各向异性介质时的反射、透射矩阵。其中,3×3的反射矩阵R为
 (6)
(6) 式中,矩阵向量R中的元素为反射系数,其两个下标分别表示入射波类型和反射波类型。R的计算公式为
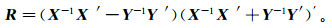 (7)
(7) 式中,X和Y是Schoenberg和Protazio通过慢度矢量、入射角和介质的弹性张量定义的阻抗矩阵。
本文将Chapman计算的弹性张量Cijkl(ω)(公式(5))带入式(6)计算反射系数RPP。由于Cijkl是ω的函数,所以反射系数可以表示成时间t、入射角θ和频率ω的函数R(t, ω, θ)。
根据Yang等[26]推导的频率分解褶积模型,在预先提取子波的情况下,时频域的地震记录可以表示为
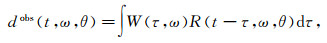 (8)
(8) 时间域的计算形式为
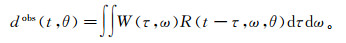 (9)
(9) 式中,W为经过时频变换得到的子波时频谱。
1.3 裂缝储层参数反演裂缝密度和时间尺度因子分别是描述裂缝结构和流体流动性的重要参数,而由于受频率和尺度独立假设的限制,以往基于数据驱动和静态等效介质模型驱动的反演方法都无法对这两个参数做出直接估计。基于裂缝密度和时间尺度因子对地震波敏感的频散响应,我们可以合理地固定其他参数并借助频变AVO反演理论构建目标函数对这两个参数进行同步估计。设待反演裂缝模型参数向量为
 (10)
(10) 式中:τfi和εfi分别为第i个时间采样点处的时间尺度因子和裂缝密度;Ns为时间采样点数。
频变AVO反演是在传统时间域进行AVO反演的基础上,增加了对振幅与频率依赖关系的考虑,也就是在时频域进行AVO反演。通过引入这一思想,裂缝储层引起的振幅频变响应就可以认为是深度、入射角和频率的函数。我们将叠前观测地震数据做时频分析处理后得到的三维时频数据体表示为
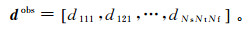
式中:dijkobs表示在第i个时间采样点、第j道、第k个频率采样点观测到的地震振幅值;Nt、Nf分别为地震道数和观测频率数。我们可以通过在时频域内搜寻模型数据与观测数据的最佳拟合向量
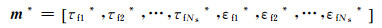
来初步定义反问题的适应度函数,即
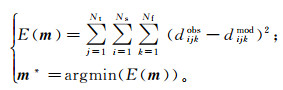 (11)
(11) 式中,dijkmod为模型在第i个时间采样点、第j道、第k个频率采样点的地震波场模拟数据。我们进一步将式(11)表示为最优化问题形式。定义目标函数为
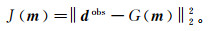 (12)
(12) 式中:G为正演算子。我们可以通过Chapman模型计算地震波纵横波速度及密度,并结合地震波场正演模拟算法(见1.2节)来构建算子G。
在实际地质条件下,裂缝参数在整个空间中大部分位置为0,或者接近于0,这就满足了压缩感知意义下的稀疏性和可压缩性,可以通过对方程(12)加入L1范数正则化约束条件避免解非线性方程或者噪声干扰给求解反问题带来不稳定性[27],即:
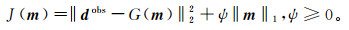 (13)
(13) 式中,ψ为正则化参数,它的作用是调节适应度函数和模型参数稀疏度之间的权重。如果ψ取值过大,那么可能造成反演结果保真度和分辨率降低;而过小的ψ会造成反演结果的剧烈抖动。本文通过小模型测试的方法选取合适的ψ值。
考虑到反演涉及参数数量多、裂缝参数与地震波振幅之间关系复杂、梯度信息难以求取等情况,我们采用了遗传算法(GA)解非线性反演问题(公式(13))。遗传算法是Holland借鉴生物界的进化规律而提出的一种全局最优化自适应概率搜索算法,在反演过程中不依赖于初值和目标函数的梯度信息,通用性强且对局部极值有一定免疫效果。
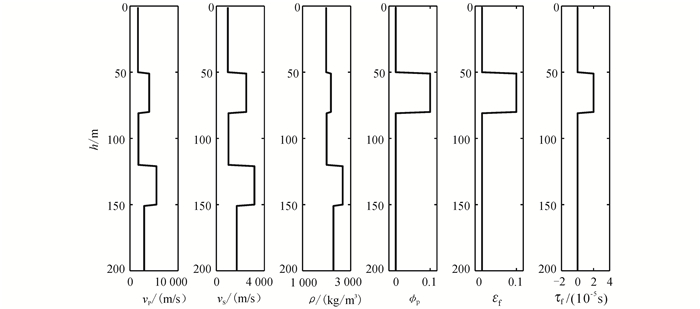
2 模型测试 2.1 一维模型测试为测试算法的有效性,笔者构建了一个200 m深度的一维模型,在50~80 m深度处有一盐水饱和裂缝储层,裂缝长度0.1 m,不含裂隙,其他模型参数曲线如图 3所示。
|
| h为深度。 图 3 一维模型参数曲线 Figure 3 1D model parameters |
|
|
在进行反演之前,需针对待反演的两个参数εf和τf做频变响应敏感分析。频变AVO反演的基础是反射系数随入射角的变化规律对频率的依赖程度。输入储层参数值的改变引起反射系数对频率的依赖性差异越大,表示反射系数频变异常对储层参数的敏感性越强,利用反射系数反演该储层参数的可行性也就越高。
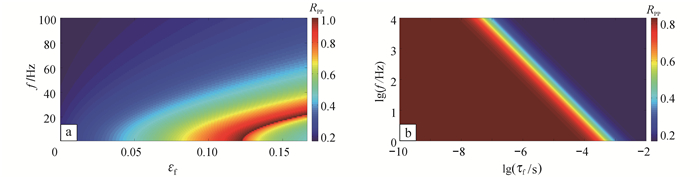
以裂缝储层的顶界面为例,计算反射系数随入射角和频率的变化关系。如图 4所示,可以观察到,除了受到入射角变化带来的整体变化趋势之外,由于地震波在裂缝储层中传播发生的速度频散现象,使得反射系数表现出了频率依赖特征,即频变响应。图 5为入射角为30°的情况下反射系数对待反演参数的频变响应。可以看出:随着裂缝密度的增大,反射系数的频变现象越来越明显(图 5a);而时间尺度因子对于反射系数频变现象的频带范围有决定性作用,当时间尺度因子为10-6~10-3 s时,反射系数在整个地震频带内(0~100 Hz)都有显著的频变响应(图 5b)。从参数敏感分析结果中,我们认为从反射系数的频变响应入手、同步反演裂缝参数εf和τf的策略具有可行性。

|
| 图 4 裂缝储层顶界面反射系数 Figure 4 Reflection coefficients for the top interface of the fractured reservoir |
|
|
|
| a.τf=2×10-5s,εf=0.01~0.15,f=1~100 Hz;b.εf=0.1,τf=10-10~10-2 s,f=1~104 Hz。 图 5 裂缝储层顶界面反射系数随裂缝参数的变化 Figure 5 Reflection coefficients varying with parameters for the top interface of the fractured reservoir |
|
|
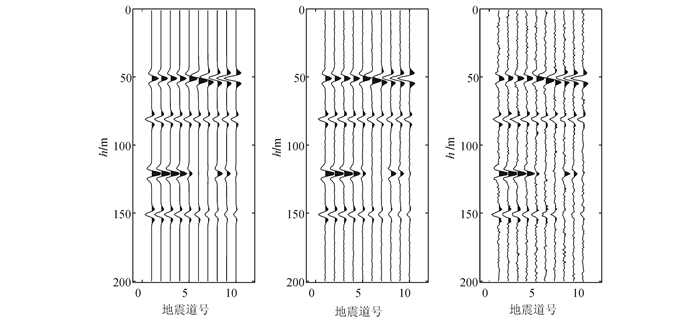
取25 Hz标准雷克子波合成模拟地震记录CMP (common middle point)道集,入射角为0°~60°,分别按照信噪比50和40 dB加入随机噪声,校正后结果如图 6所示。可以看出在频散层顶、底界面,反射系数的频变现象对地震波的波形有明显的改造。
|
| 图 6 无噪(左)、SNR=50 dB (中)、SNR=40 dB (右)情况下模型合成地震记录 Figure 6 Seismic synthetic record without (left), SNR=50 dB (middle), and SNR=40 dB (right) Gaussian noise |
|
|
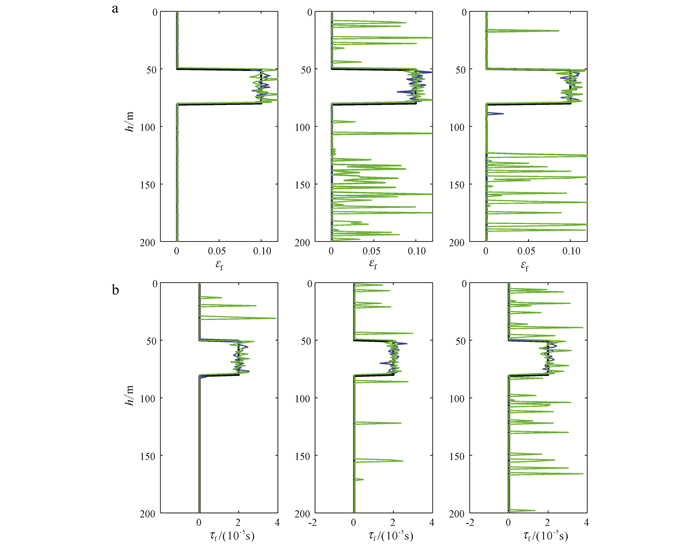
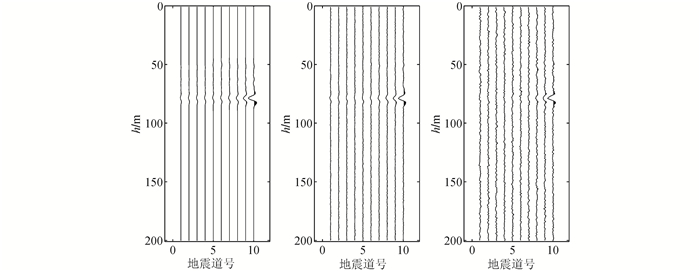
现将图 6作为输入观测数据,分别依据公式(12)和公式(13)进行未加入约束和加入约束的频变AVO反演,ψ=0.2。时频分析方法采用连续小波变换(CWT),频率采样范围为1~100 Hz,采样间隔1 Hz。遗传算法种群规模为500,交配概率为0.9,变异概率为0.2,最大迭代次数为8。图 7为3种噪声水平下的反演结果,可以看出反演结果对原模型都有一定程度的还原。此外,对比加入L1范数约束前、后的反演结果不难发现:在参数估计值总体趋势上(即低频成分),二者均能对裂缝储层有较好的描述;但是加入了约束后的反演结果稳定性更好,抖动更少,抗噪音干扰能力更强,对我们定量描述裂缝更有利。做模拟记录与反演结果合成记录的残差(图 8)可以看出,在近道(约θ≤40°)情况下,残差中基本不包含模型相关的有效信息;在远道(约θ>40°)情况下,由于反射系数高阶项的剧烈变化在一定程度上影响了拟合的精度,残差中包含了少量有效信息。
|
|
a.裂缝密度;b.时间尺度因子。 黑色曲线为原模型;绿色曲线为未加入约束的反演结果;蓝色曲线为加入L1范数约束的反演结果。 图 7 无噪(左)、SNR=50 dB (中)、SNR=40 dB (右)情况下裂缝参数反演结果 Figure 7 Inversion result of data without (left), with SNR=50 dB (middle), and SNR=40 dB (right) Gaussian noise |
|
|
|
| 图 8 无噪(左)、SNR=50 dB (中)、SNR=40 dB (右)情况下反演结果合成记录与模型记录之间的残差 Figure 8 Residual error of seismic synthetic record of the model and inversion result of data without (left), with SNR=50 dB (middle), and SNR=40 dB (right) Gaussian noise |
|
|
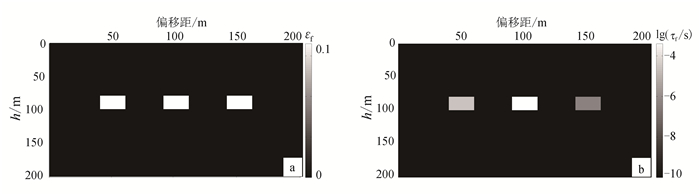
为测试该方法在复杂区域构造中裂缝描述的有效性,笔者构造了一个200 m×200 m的二维岩性剖面模型(截取Marmousi 2模型水平方向1~200 m、深度方向300~500 m为背景速度和密度模型),在80 m深度处加入3个20 m×20 m的矩形裂缝性砂岩储层(图 9),裂缝密度为0.1,孔隙度为0.1,分别为盐水饱和、油饱和和天然气饱和状态。储层参数如表 1所示,待反演参数模型如图 10所示。

|
| 图 9 二维速度模型 Figure 9 2D velocity model |
|
|
|
| 图 10 裂缝参数原始模型 Figure 10 The original model of fracture parameters |
|
|
| 储层 | 密度/ (kg/m3) |
纵波速 度/(m/s) |
横波速 度/(m/s) |
时间尺度 因子/s |
| 盐水 | 2 180 | 3 820 | 2 237 | 2×10-5 |
| 油 | 2 150 | 3 761 | 2 193 | 4×10-4 |
| 天然气 | 2 076 | 2 193 | 2 155 | 4×10-7 |
根据模型参数合成200个CMP道集作为输入数据,分别考虑无噪声和信噪比为40 dB两种情况,正演参数与上节一维模型相同。再次根据L1范数约束的频变反演(公式(13))方法逐道集进行裂缝参数同步估计。考虑到二维模型带来的较大计算量,把遗传算法种群规模减少为100,最大迭代次数减少为2,其他反演输入参数均与上节相同。
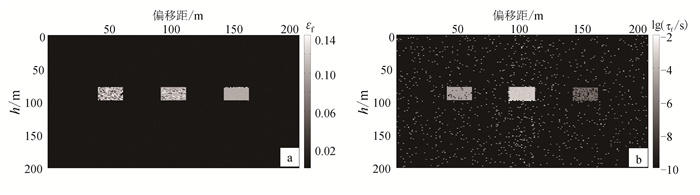
输入无噪声地震记录,裂缝参数同步反演结果如图 11所示。对比原始模型(图 10),我们可以发现,裂缝储层的空间位置和形状较为清晰和准确地反映在了反演结果中,并且裂缝参数值得到了较好的还原。另外可以观察到,由于考虑计算成本,没有出现在遗传算法中使用大种群规模和多次数迭代造成的反演结果中存在的一些虚假的高频数值抖动(尤其是时间尺度因子)的现象;但我们认为这些抖动分散且不连续,不会对构造解释和流体识别工作造成较大阻碍。
|
| 图 11 无噪情况裂缝参数反演结果 Figure 11 Inverted fracture parameters for noise-free data |
|
|
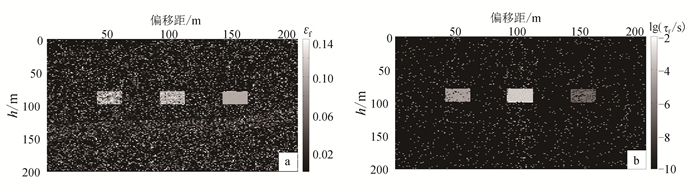
图 12为输入有噪声数据的同步反演结果,可以看到即使在较强的噪声背景下(SNR=40 dB),我们提出的基于频变AVO反演的参数估计算法仍然对裂缝储层形状、位置和岩石物理特性具有一定的描述精度。另外我们发现,相比于时间尺度因子,裂缝密度的反演结果更容易受到噪声水平的干扰。这是由于高斯噪声在频带内的均匀分布对频散范围(时间尺度因子决定)的影响较为整体,而对幅值(裂缝密度决定)的影响较为随机。在以后在实际资料处理和解释工作中可以参考这个规律。
|
| 图 12 SNR=40 dB时裂缝参数反演结果 Figure 12 Inverted fracture parameters for noisy data (SNR=40 dB) |
|
|
本文提出了一种基于频变AVO理论与Chapman等效介质模型的裂缝密度和流体时间尺度因子的同步反演方法,得出结论如下:
1) 本文提出的模型驱动的频变AVO反演算法充分利用了Chapman模型可以频率依赖地描述裂缝储层这一优势,更加符合裂缝储层的实际岩石物理特征。
2) 经过一维和二维模型测试,证明本文方法可以在保证精度的前提下,同步反演裂缝密度和时间尺度因子两个关键裂缝参数,这是基于弹性假设的常规AVO反演方法无法做到的。另外,加入L1范数约束反演,可以使估算结果更加稳定且不易受噪声干扰。
3) 本文方法为最大化地利用叠前地震资料解决裂缝储层描述问题提供了一种有效的方案,有广阔的应用前景。但运算量较大、地震资料品质要求较高和依赖测井或先验资料等弊端仍需进一步研究改进,以达到实际应用的目的。
| [1] | Engelder T, Lash G G, Uzcátegui R S. Joint Sets that Enhance Production from Middle and Upper Devonian Gas Shales of the Appalachian Basin[J]. AAPG Bulletin, 2009, 93 (7) : 857-889. DOI:10.1306/03230908032 |
| [2] | Engelder T. Joints and Shear Fractures in Rock[M]//Fracture Mechanics of Rock. London:Academic Press Inc (London) Ltd, 1987:27-69. |
| [3] | Narr W, Schechter D W, Thompson L B. Naturally Fractured Reservoir Characterization[M]. Richardson: Society of Petroleum Engineers, 2006. |
| [4] | 张国君, 冯晅, 王典, 等. 裂隙性油气藏发展现状[J]. 吉林大学学报(地球科学版), 2008, 38 (增刊 1) : 43-47. Zhang Guojun, Feng Xuan, Wang Dian, et al. Study on the Recovery of Aliasing Seismic Data Based on the Compressive Sensing Theory[J]. Journal of Jilin University (Earth Science Edition), 2008, 38 (Sup. 1) : 43-47. |
| [5] | 张广智, 陈怀震, 印兴耀, 等. 基于各向异性AVO的裂缝弹性参数叠前反演方法[J]. 吉林大学学报(地球科学版), 2012, 42 (3) : 845-851. Zhang Guangzhi, Chen Huaizhen, Yin Xingyao, et al. Method of Fracture Elastic Parameter Inversion Based on Anisotropic AVO[J]. Journal of Jilin University (Earth Science Edition), 2012, 42 (3) : 845-851. |
| [6] | Rüger A, Tsvankin I. Using AVO for Fracture De-tection:Analytic Basis and Practical Solutions[J]. The Leading Edge, 1997, 16 (10) : 1429-1434. DOI:10.1190/1.1437466 |
| [7] | 刘财, 刘宇巍, 冯晅, 等. 基于方位相交的纵波AVA数据运用SVD反演HTI介质裂缝密度[J]. 吉林大学学报(地球科学版), 2013, 43 (5) : 1655-1662. Liu Cai, Liu Yuwei, Feng Xuan, et al. Invert Crack Density of HTI Media by Using SVD Based on PP-Wave AVA Data from Crossing Seismic Survey Lines[J]. Journal of Jilin University (Earth Science Edition), 2013, 43 (5) : 1655-1662. |
| [8] | 刘喜武, 董宁, 刘宇巍. 裂缝性孔隙介质频变AVAZ反演方法研究进展[J]. 石油物探, 2015, 54 (2) : 210-217. Liu Xiwu, Dong Ning, Liu Yuwei. Progress on Frequency-Dependent AVAZ Inversion for Characterization of Fractured Porous Media[J]. Geophysical Prospecting for Petroleum, 2015, 54 (2) : 210-217. |
| [9] | 桂金咏, 高建虎, 雍学善, 等. 基于双相介质理论的储层参数反演方法[J]. 地球物理学报, 2015, 58 (9) : 3424-3438. Gui Jinyong, Gao Jianhu, Yong Xueshan, et al. Inversion of Reservoir Parameters based on Dual-Phase Media Theory[J]. Chinese Journal of Geophysicsics, 2015, 58 (9) : 3424-3438. |
| [10] | Guo Z Q, Li X Y, Liu C, et al. AVO Inversion Based on a Thin Bed Model for the Characterization of Fracture Zones in the Bakken Formation[C]//75th EAGE Conference & Exhibition.[S.1.]:EAGE, 2013. |
| [11] | 兰慧田.裂缝性孔隙介质波场模拟与频变AVO储层参数反演[D].长春:吉林大学, 2014. Lan Huitian. Wave Field Modeling in Fractured Porous Media and Frequency-Dependent AVO Reservoir Parameters Inversion[D]. Changchun:Jilin University, 2014. |
| [12] | Hudson J A. Wave Speeds and Attenuation of Elastic Waves in Material Containing Cracks[J]. Geophysical Journal International, 1981, 64 (1) : 133-150. DOI:10.1111/j.1365-246X.1981.tb02662.x |
| [13] | Schoenberg M, Sayers C M. Seismic Anisotropy of Fractured Rock[J]. Geophysics, 1995, 60 (1) : 204-211. DOI:10.1190/1.1443748 |
| [14] | Thomsen L. Elastic Anisotropy due to Aligned Cra-cks in Porous Rock[J]. Geophysical Prospecting, 1995, 43 (6) : 805-829. DOI:10.1111/gpr.1995.43.issue-6 |
| [15] | Parra J O. Poroelastic Model to Relate Seismic Wave Attenuation and Dispersion to Permeability Anisotropy[J]. Geophysics, 2000, 65 (1) : 202-210. DOI:10.1190/1.1444711 |
| [16] | 孟庆生, 何樵登, 朱建伟, 等. 基于BISQ模型双相各向同性介质中地震波数值模拟[J]. 吉林大学学报(地球科学版), 2003, 33 (2) : 217-221. Meng Qingsheng, He Qiaodeng, Zhu Jianwei, et al. Seismic Modeling in Isotropic Porous Media Based on BISQ Model[J]. Journal of Jilin University (Earth Science Edition), 2003, 33 (2) : 217-221. |
| [17] | Chapman M, Zatsepin S V, Crampin S. Derivation of a Microstructural Poroelastic Model[J]. Geophysical Journal International, 2002, 151 (2) : 427-451. DOI:10.1046/j.1365-246X.2002.01769.x |
| [18] | Eshelby J. The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems[J]. Proceedings of the Royal Society of London, 1957, 241 : 376-396. DOI:10.1098/rspa.1957.0133 |
| [19] | Chapman M, Maultzsch S, Liu E, et al. The Effect of Fluid Saturation in an Anisotropic Multi-Scale Equant Porosity Model[J]. Journal of Applied Geophysics, 2003, 54 (3) : 191-202. |
| [20] | Liu E, Maultzsch S, Chapman M, et al. Frequency-Dependent Seismic Anisotropy and Its Implication for Estimating Fracture Size in Low Porosity Reservoirs[J]. The Leading Edge, 2003, 22 (7) : 662-665. DOI:10.1190/1.1599692 |
| [21] | Maultzsch S, Chapman M, Liu E, et al. Modelling Frequency-Dependent Seismic Anisotropy in Fluid-Saturated Rock with Aligned Fractures:Implication of Fracture Size Estimation from Anisotropic Measurements[J]. Geophysical Prospecting, 2003, 51 (5) : 381-392. DOI:10.1046/j.1365-2478.2003.00386.x |
| [22] | Tillotson P, Chapman M, Best A I, et al. Obser-vations of Fluid-Dependent Shear-Wave Splitting in Synthetic Porous Rocks with Aligned Penny-Shaped Fractures[J]. Geophysical Prospecting, 2011, 59 (1) : 111-119. DOI:10.1111/gpr.2010.59.issue-1 |
| [23] | Chapman M, Liu E, Li X Y. The Influence of Fluid Sensitive Dispersion and Attenuation on AVO Analysis[J]. Geophysical Journal International, 2006, 167 (1) : 89-105. DOI:10.1111/gji.2006.167.issue-1 |
| [24] | Brown R J S, Korringa J. On the Dependence of the Elastic Properties of a Porous Rock on the Compressibility of the Pore Fluid[J]. Geophysics, 1975, 40 (4) : 608-616. DOI:10.1190/1.1440551 |
| [25] | Schoenberg M, Protazio J. "Zoeppritz" Rationalized, and Generalized to Anisotropic Media[J]. The Journal of the Acoustical Society of America, 1990, 88 (Sup. 1) : S46-S46. |
| [26] | Yang J, Geng J, Zhao L. Frequency Decomposition Convolutional Model for AVO/AVF Analysis in Viscoelastic Media[C]//2015 SEG Annual Meeting. New Orleans:Society of Exploration Geophysicists, 2015:613-618. |
| [27] | Liu C, Song C, Lu Q, et al. Impedance Inversion Based on L1 Norm Regularization[J]. Journal of Applied Geophysics, 2015, 120 : 7-13. DOI:10.1016/j.jappgeo.2015.06.002 |



