2. 中国石油勘探开发研究院西北分院, 兰州 730020;
3. 中石化江苏油田分公司物探研究院, 南京 210046
2. Research Institute of Petroleum Exploration & Development-Northwest, PetroChina, Lanzhou 730020;
3. Geophysical Prospecting Research Institute, JOECO, SINOPEC, Nanjing 210046
0 引言
在地震勘探数据采集过程中,由于受到施工条件的影响,或是由于仪器可能出现的故障以及海上地震资料采集时震源与最近检波点存在一定的距离,通常会造成近偏移距数据缺失,以及野值道和某些测线方向上存在道间距太大的情况。数据缺失不仅导致地震信息的丢失,还可能严重影响诸如波动方程偏移成像等多道处理算法的精度,从而对后续的工作造成不良影响。
目前存在多种数据重构或地震道插值的方法,诸如预测误差滤波法地震道插值[1]、倾向-样条插值法[2]、傅里叶变换[3-5]、利用数据压缩特性或稀疏特性的方法[6-8]、Radon变换[9-12]等。预测误差滤波法和倾向-样条插值法对动校正速度具有较高要求;而且如果同相轴是倾斜的或者当数据中含有噪声时,重建结果中可能会出现假的同相轴,导致重建效果差。采样傅里叶变换法[3-5]可以在频率-波数域实现地震道插值,利用曲波变换的压缩特性可以重建缺失的地震数据[6],利用压缩感知和稀疏反演技术也能够进行缺失数据重建[7-8],一般不用这些方法进行近偏移距的外推。利用抛物Radon变换法进行近偏移距数据重构是目前比较常用的方法。黄新武等[9]给出了基于抛物Radon变换的地震数据重构方法,但单纯基于抛物线Radon变换的地震道插值与外推方法通过多次迭代获得重建数据,需要较多的迭代次数。王维红等[10]在抛物Radon变换的基础上,通过与道均衡方法相结合,极大地减少了抛物线Radon正、反变换的次数,提高了计算效率。李晶晶等[12]研究了相对保幅的抛物线Radon变换地震道重建方法,利用较少的迭代次数达到相对保幅重建的目的。Radon变换的变种(如λ-f域抛物Radon变换)也能够实现地震数据重建[13]。然而,基于抛物Radon变换法进行数据重构的基本假设是经过动校正数据的同相轴接近抛物线,所以该方法不适应存在绕射等复杂波场的数据。随着地震采集和处理技术的进步,兴起了五维插值方法[14-16],地震数据可以在纵测线-横测线-炮检距-方位角-频率域进行重建,能够得到较好的重建效果;但该方法依旧是在已有的数据基础上进行数学变换,然后在新的数据域中实现数据重建,本质上并没有得到更多的数据信息。
多次波通常被当作噪声而被衰减和消除[17-19]。然而,多次波是地震信号在反射界面之间的多次反射,它和一次波一样,经过适当方法处理后,能够反映地下的地质构造特征;因此,可以利用多次波获取更加丰富的地质构造信息,实现利用多次波数据的插值[21-24]和成像[20,24]。Curry等[21]使用多次波和预测误差滤波实现了近偏移距数据的重构:当待重构的地震数据较为复杂时,滤波器可能难以拾取所有同相轴的信息而导致重构效果变差,该方法使用共轭梯度法计算预测误差滤波器,能够提高运算速度;但计算量仍然较大,计算效率不高。郭书娟等[22-24]使用多次波和最小平方匹配滤波法进行了近偏移距数据重构,由于该方法采用的是一维滤波,且用来进行数据重构的匹配滤波器是多个滤波器的均值,因此重构数据的同相轴在横向上变化不自然;此外,在时间域计算匹配滤波因子,计算量依然较大。
本文分析并研究了由表层多次波构建准一次波的方法,在时间-空间滑动窗口内利用准一次波和对应的一次波计算二维匹配滤波器,进而利用该滤波器进行数据重构。由于整个计算过程都在频率域进行,避免了基于维纳滤波方法求取滤波器的大量计算,并且使用快速傅里叶变换算法,提高了计算效率。用该方法对Sigsbee 2B数据进行处理并对实际资料进行测试,以验证它的可行性。
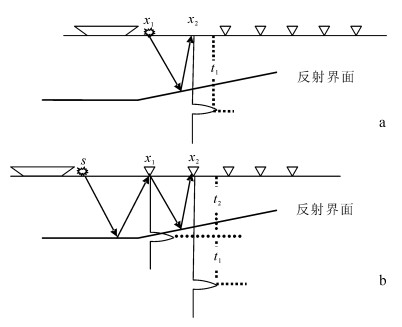
1 准一次波构建图 1是海上地震资料采集示意图。当空气枪在x1处激发时,由于最近的接收点与x1之间有一定的距离,导致x2处无法记录到地下反射信息,因此存在近偏移距数据的缺失。假设x2处有检波器,则地震波从x1处出发,被地下界面反射到达x2处的时间为t1(图 1a)。随着勘探船的移动,在s处激发时(图 1b),位于x1处的接收点可以接收到地下界面的反射信息,地震波从s处向下传播并在地下界面发生反射,到达检波器x1处被接收得到一次波,此过程需要时间为t2;同时,一次波在x1处又被反射向地下传播,进而形成多次波并在x2处被接收,这段过程需要时间为t1。因此,x2接收的多次波,其传播时间为t1+t2。将x1处的地震记录与x2处的地震记录做互相关、x1处接收到的一次波与对应的多次波(多次波包含在x2记录中)互相关,可以消除x1处一次波的传播时间t2,得到拟激发点位于x1处、拟接收点位于x2处的新的地震数据[21-22, 24]。它与一次波的运动学特征非常相似,因此称它为准一次波:
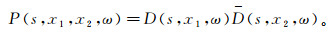 (1)
(1)
|
| 图 1 利用多次波构建准一次波示意图 Figure 1 Illustration of constructing pseudo primaries using multiples |
|
|
式中:s是激发点位置;x1和x2是接收点位置;ω是频率;D(s, x1, ω)、D(s, x2, ω)是同时含一次波和表层多次波的地表接收波场,D(s, x2, ω)是D(s, x2, ω)的共轭;P(s, x1, x2, ω)是激发点位于x1处、接收点位于x2处的准一次波场。固定激发点的位置x1不变,不断改变x2,则得到一个激发点位于x1处的准一次波炮记录。
然而,x1处的一次波与非对应的多次波做互相关,并不能得到与一次波类似的准一次波,它们的互相关能量将以随机噪音的形式出现。为提高信噪比,应先确定某一个位置作为准一次波炮记录的虚拟震源位置,然后在互相关的过程中,将所有炮集位于虚拟震源位置的地震数据与其他道互相关结果进行叠加[21-22, 24],叠加结果就是准一次波炮记录。构建准一次波时,输入数据不必进行一次波和多次波的分离,成对的一次波和与它相对应多次波互相关的能量通过各炮叠加能够逐渐得到加强并保留下来;而那些非成对的互相关能量则在叠加的过程中相互削弱,以类似于随机量叠加的形式在各炮叠加的过程中相互抵消,因此不会出现真正的同相轴。通常采用如下方法求取准一次波:
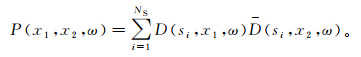 (2)
(2) 式中:si为参与互相关的第i炮的激发点位置;i=1, 2, …, NS,NS为参与互相关的总炮数;D(si, x1, ω)、D(si, x2, ω)是同时含一次波和多次波的第i炮的波场,D(si, x2, ω)是D(si, x2, ω)的共轭;P(x1, x2, ω)是激发点位置为x1、接收点位置为x2的准一次波场。
由于没有压制参与互相关数据中的高阶多次波,成对一次波和一阶多次波互相关、一阶多次波和二阶多次波互相关都可以得到准一次波;同理,一次波与二阶多次波进行互相关,可以得到准一阶多次波。因此,通过互相关方法(公式(2))计算出的准一次波记录中不仅含有准一次波,而且同时含有准多次波。
由于空气的速度和密度很小,空气与地面(或者水面)的分界面是一个良好的反射界面,该分界面具有较大的波阻抗差,为表层多次波的产生提供了必要的条件[19]。由于球面扩散和地层吸收的影响,随着传播距离的增加,地震波的能量逐渐减小,导致深层的界面没有对应的表层多次波;因此,本文方法一般不对深层数据进行数据重构,且不能用于表层多次波不发育地区的数据重构。
2 近偏移距数据重构准一次波和实际一次波具有相似的运动学特征[21],但相位和振幅方面与一次波的差异较大;此外,准一次波数据中也可能有乱真同相轴的存在。因此,准一次波不能直接用于缺失的地震数据重构。然而,可以在滑动时间-空间窗口内利用准一次波计算匹配滤波器,然后用匹配滤波器进行数据重构,从而消除相位和振幅等差异,使准一次波与一次波具有相似运动学特征的特点得以利用。
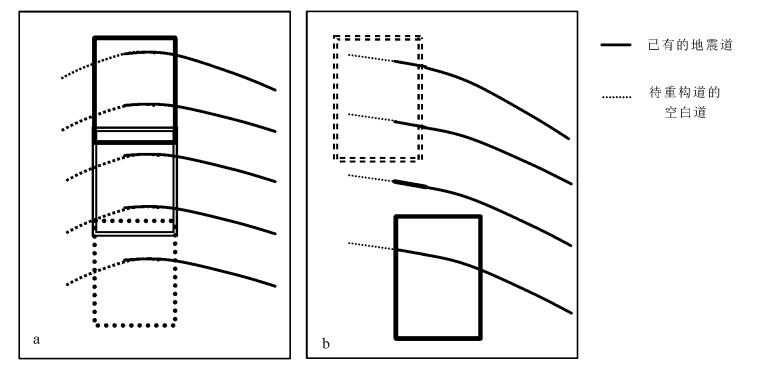
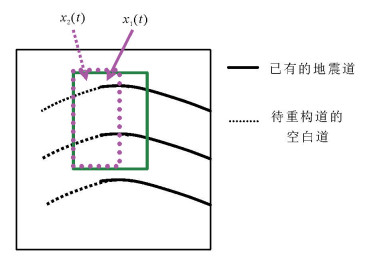
数据重构是在时间-空间数据窗口内进行的[22-24]。图 2是时间和空间窗口的滑动示意图。图 2a在虚曲线表示的空白道附近开一个窗口,该窗口包含已有的地震道和待重构的空白道。利用该窗口已有的地震数据(一次波数据)和对应位置的准一次波数据计算匹配滤波器,然后利用该滤波器重构缺失数据并校正振幅,最后用重构的数据填充窗口中的缺失道,即完成这个数据窗口内缺失数据的重构。在时间上按照浅、中、深层的顺序滑动数据窗口,缺失的地震数据逐步得到重构,如图 2a所示;窗口重叠的部分用两次重构数据进行线性加权。当从浅至深所有的缺失数据都已经重构好,则窗口需要在空间方向上滑动,如图 2b所示,数据窗口由实线窗的位置移到相邻空间的虚线窗位置,继续按照上述方法重构缺失数据。如此依次进行,直到完成所有近偏移距数据的重构。
|
| 图 2 时间方向(a)与空间方向(b)滑动窗示意图 Figure 2 Illustration of time (a) and spatial (b) sliding windows |
|
|
设图 2a窗口内实曲线表示的已有地震数据的一道为x1(t),对应位置的准一次波为p1(t),则存在一个匹配滤波器c (t),该滤波器对准一次p1(t)滤波后逼近地震道x1(t):
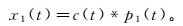 (3)
(3) 式中,*表示褶积。对公式(3)两端分别作傅里叶变换,得到频率域的匹配滤波器为
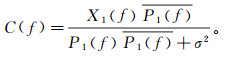 (4)
(4) 式中:C(f)、P1(f)和X1(f)分别是c(t)、p1(t)和x1(t)的频率域表达;P1(f)是P1(f)的共轭;σ2是数值很小的正数,起到防止分母为0的作用。
假设x1(t)的相邻道x2(t)是缺失的,x2(t)对应的准一次波为p2(t),则利用匹配滤波器c (t)能够计算出缺失地震道x2(t),从而实现缺失地震数据的重构:
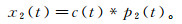 (5)
(5) 对公式(5)两端分别作傅里叶变换,并将公式(4)代入,得到频率域的数据重构公式:
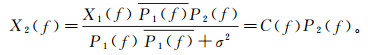 (6)
(6) 式中,X2(f)和P2(f)是x2(t)和p2(t)的频率域表达。
类似地,在二维情况下,有二维匹配滤波器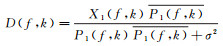
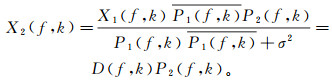 (7)
(7) 式中:X1(f, k),X2(f, k)和P1(f, k),P2(f, k)是对应一次波和准一次波的二维频率域表达;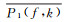
通过匹配滤波器得到的重构数据,其相位和波形与原始数据很接近,但振幅存在一些差异,需要对振幅进行进一步校正。本文采用均方根振幅校正法进行振幅校正。图 3是图 2a窗口的放大显示。为满足振幅校正的需要,待重构道可以包含一部分已有的原始数据x1(t),设其道数为M1,与它对应的由准一次波重构的数据为y1(t);图 3虚线窗内由准一次波重构的数据为x2(t),设其道数为M2。则它们的均方根振幅Ax1,Ay1和Ax2分别为:
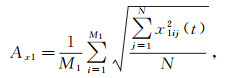 (8a)
(8a) 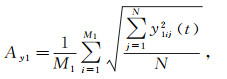 (8b)
(8b) 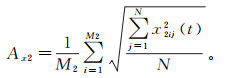 (8c)
(8c)
|
| 图 3 均方根振幅校正示意图 Figure 3 Illustration of root mean square amplitude correction |
|
|
式中:N为用于均方根振幅校正的时间长度;x1ij(t)、y1ij(t)、x2ij(t)分别为视窗内第i道第j个采样点的原始数据、与原始数据对应的重构数据、重构数据。则均方根振幅的校正因子A的计算公式为
 (9)
(9) 用振幅校正因子对重构数据进行振幅校正,经过振幅校正的重构数据在相位、波形和振幅上都具有较高的准确度。
3 数值试验为了验证方法的有效性,使用Sigsbee 2B数据进行近偏移距数据的重构试验。分别利用准一次波和一维匹配滤波的方法(公式(6))及二维匹配滤波的方法(公式(7))进行数据重构,并对比分析两种方法的重构效果。最后通过实际资料的测试验证该方法的正确性。
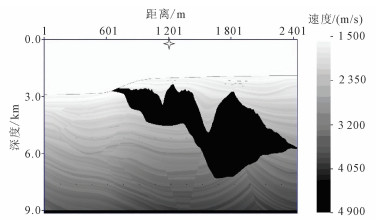
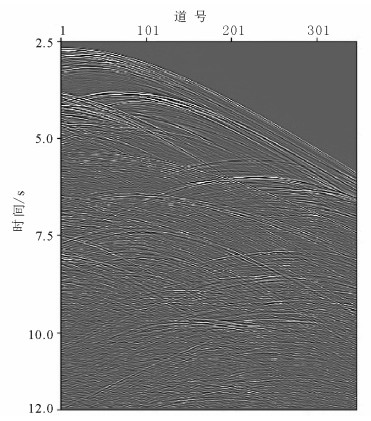
3.1 Sigsbee 2B数据试验为验证数据重构方法对复杂数据的适应性,选取Sigsbee 2B模型数据进行试验。SMAART (subsalt multiples attenuation and reduction team)推出的Sigsbee 2B模型数据是主要用于多次波数据处理的标准模型数据。该模型数据共496炮,左边放炮;前142炮的接收道数从65道逐渐增加到347道,增加速度为2道/炮,143炮之后为每炮348道接收;道间距22.86 m (75 ft ft①),记录长度为12 s,时间采样率8 ms。图 4是Sigsbee 2B的速度模型,它包含一个用于产生多次波的起伏海底界面。图 5是Sigsbee 2B模型数据中含多次波的一个单炮记录,其炮点位置在图 4的星号位置。
① (英尺)为非法定计量单位,1 ft=0.304 8 m
|
| 图 4 Sigsbee 2B速度模型 Figure 4 Sigsbee 2B velocity model |
|
|
|
| 图 5 含多次波的炮记录 Figure 5 Shot gathers with multiples |
|
|
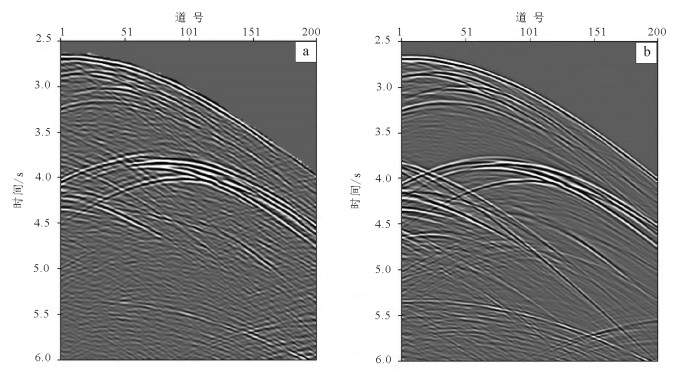
利用公式(2)从含有多次波的炮记录中构建准一次波。图 6a所示为切除了浅层相干噪音的准一次波记录;为清晰地展示重构效果,横向上显示200道,时间方向上只截取2.5~6.0 s的部分显示。图 6b是一次波炮记录,它与图 6a的准一次波记录具有相同的炮点位置。从图 6a和图 6b可以看出,准一次波和对应的一次波整体上非常相似,但准一次波的信噪比更低,且有些细节不如一次波的清晰。
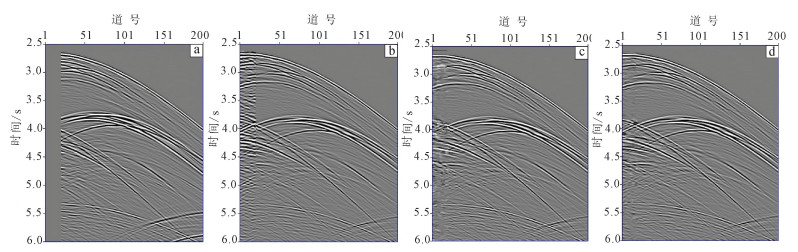
图 7a将图 6b的20道近偏移距赋零,从而造成457.2 m的近偏移距缺失。图 7b将图 7a的缺失道直接用准一次波替换。从图 7a、b可以看出,准一次波和一次波同相轴的振幅、相位等特征不一致,说明准一次波不能直接用于缺失数据的重建。图 7c是利用准一次波计算一维匹配滤波器,然后进行数据重构得到的剖面。从图 7c中可以看出,重构的同相轴与未缺失部分的同相轴特征基本类似,但重构数据有些模糊,重构效果不理想。图 7d是利用准一次波计算二维匹配滤波器,然后进行数据重构得到的剖面。从图 7d中可以看出,重构的同相轴与未缺失部分的同相轴具有类似的特征,与一维匹配滤波重构的数据相比,二维匹配滤波重构的数据更清晰,具有较好的重构效果。
|
| a.近偏移距缺失20道;b.准一次波直接替代缺失道;c.一维匹配滤波重构剖面;d.二维匹配滤波重构剖面。 图 7 Sigsbee 2B数据的重构 Figure 7 Reconstruction of Sigsbee 2B data |
|
|
图 8是20道原始数据及它与图 7c、d对应地震道的差值;为清楚地显示细节,采用波形加变面积的显示方式。从图 8中可以看出:一维匹配滤波重构的误差较大,采用二维匹配滤波重构的误差更小;在4 s附近的重构误差较大,是由于准一次波(图 6a)与对应的一次波(图 6b)相比,在4 s附近个别同相轴能量极弱甚至缺失,是以进行数据重构时,匹配滤波产生了较大的误差。
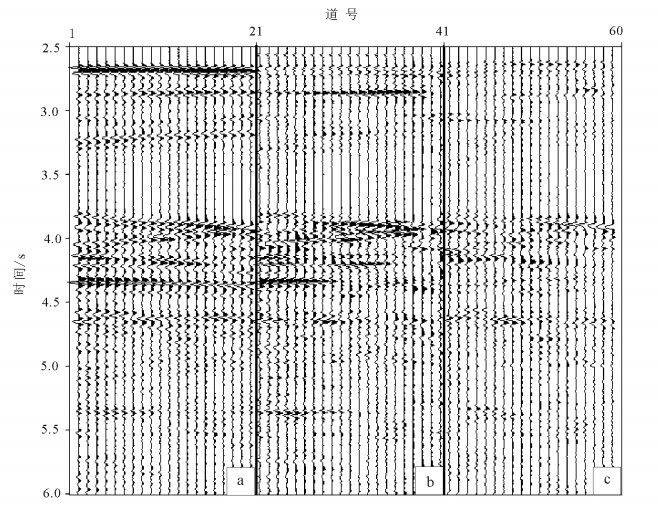
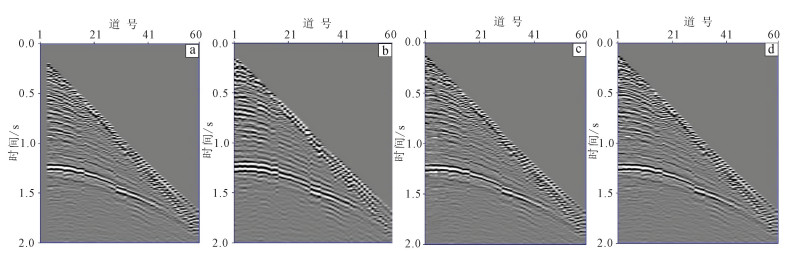
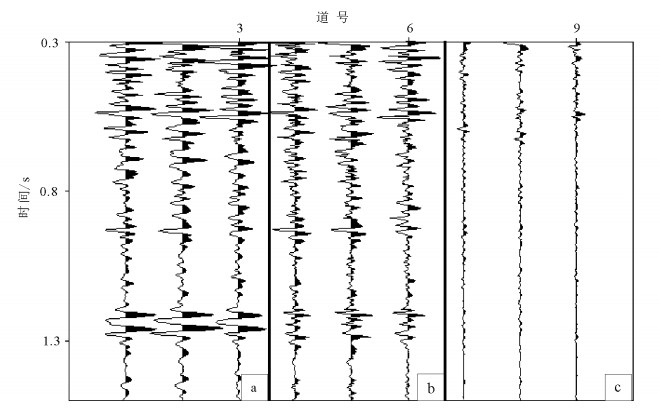
图 9a为某探区实际地震资料的原始记录,最小炮检距为150 m,道间距为50 m,因此从零偏移距到最近偏移距之间存在3道数据缺失(图中的零值道)。为了方便数据重构前后的对比,从图 9a近偏移距数据中切除3道数据,从而得到连续缺失6道的数据(偏移距缺失范围是0~300 m)。图 9b是采用公式(2)计算的准一次波,与未缺失的一次波(图 9a)相比,两者同相轴的相位存在差异,但具有类似的运动学特征。图 9c是采用一维匹配滤波方法的重构剖面,缺失数据得到重构,但重构效果并不理想。图 9d是采用二维匹配滤波方法的重构剖面,相对一维匹配滤波方法的重构剖面,具有较好的重构效果。图 10是图 9a中切除的3道数据以及它与图 9c、d对应位置数据的差值。从图 10中可以看出,采用一维匹配滤波重构的误差较大,采用二维匹配滤波重构的误差更小。
|
| a.原始地震数据;b.准一次波数据;c.一维匹配滤波重构剖面;d.二维匹配滤波重构剖面。 图 9 实际资料的重构 Figure 9 Reconstruction of real seismic data |
|
|
|
| 图 10 3道原始数据(a)及它与图 9c和图 9d对应地震道的差值(b、c) Figure 10 Three traces of original data (a) and its differences with the corresponding traces of Fig. 9c (b) and Fig. 9d (c) |
|
|
本文分析并研究了利用表层多次波和匹配滤波方法的近偏移距数据重构方法,通过对Sigsbee 2B数据的处理及实际资料的测试,验证了该方法的准确性,得出如下结论:
1) 采用互相关方法提取的准一次波与一次波具有相似的运动学特征,但在振幅和相位等方面与一次波存在差异,因此不能直接替代缺失数据。
2) 利用准一次波计算出的一维匹配滤波器和二维匹配滤波器都能进行数据重构,但二维匹配滤波具有更好的重构效果。
3) 本方法是对准一次波进行二维滤波处理,将滤波后的数据替代缺失道,从而完成数据重构。由于地震波的能量随着传播距离的增大而减弱,导致深层界面对应的表层多次波很弱,因此使用本文方法一般不对深层数据进行数据重构。
| [1] | Spitz S. Seismic Trace Interpolation in F-X Domain[J]. Geophysics, 1991, 56 (6) : 785-794. DOI:10.1190/1.1443096 |
| [2] | Verschuur D. Surface-Related Multiple Elimination:An Inversion Approach[D]. Delft:Delft University of Technology, 1991. https://www.researchgate.net/publication/27343211_Surface-related_multiple_elimination_an_inversion_approach |
| [3] | 高建军, 陈小宏, 李景叶, 等. 基于非均匀Fourier变换的地震数据重建方法研究[J]. 地球物理学进展, 2009, 24 (5) : 1741-1747. Gao Jianjun, Chen Xiaohong, Li Jingye, et al. Study on Reconstruction of Seismic Data Based on Nonuniform Fourier Transform[J]. Progress in Geophysics, 2009, 24 (5) : 1741-1747. |
| [4] | 国九英, 周兴元. F-K域等道距道内插[J]. 石油地球物理勘探, 1996, 31 (2) : 211-218. Guo Jiuying, Zhou Xingyuan. Iso-Spaced Trace Interpolation in F-K Domain[J]. Oil Geophysical Prospecting, 1996, 31 (2) : 211-218. |
| [5] | 张文颖.保幅性三维傅里叶变换叠前道内插技术研究[D].青岛:中国石油大学(华东), 2011. Zhang Wenying. Amplitude-Preserved Prestack Interpolation of Seismic Data with 3-D Fourier Transform[D]. Qingdao:China University of Petroleum (East China), 2011. |
| [6] | 刘国昌, 陈小宏, 郭志峰, 等. 基于Curvelet变换的缺失地震数据插值方法[J]. 石油地球物理勘探, 2011, 46 (2) : 237-246. Liu Guochang, Cheng Xiaohong, Guo Zhifeng, et al. Missing Seismic Data Rebuilding by Interpolation Based on Curvelet Transform[J]. Oil Geophysical Prospecting, 2011, 46 (2) : 237-246. |
| [7] | 韩立国, 张莹, 韩利, 等. 基于压缩感知和稀疏反演的地震数据低频补偿[J]. 吉林大学学报(地球科学版), 2012, 42 (增刊3) : 259-264. Han Liguo, Zhang Ying, Han Li, et al. Compressed Sensing and Sparse Inversion Based Low-Frequency Information Compensation of Seismic Data[J]. Journal of Jilin University (Earth Science Edition), 2012, 42 (Sup.3) : 259-264. |
| [8] | 周亚同, 王丽莉, 蒲青山. 压缩感知框架下基于K-奇异值分解字典学习的地震数据重建[J]. 石油地球物理勘探, 2014, 49 (4) : 652-660. Zhou Yatong, Wang Lili, Pu Qingshan. Seismic Data Reconstruction Based on K-SVD Dictionary Learning Under Compressive Sensing Framework[J]. Oil Geophysical Prospecting, 2014, 49 (4) : 652-660. |
| [9] | 黄新武, 吴律, 牛滨华. 基于抛物线拉东变换的地震道重构[J]. 中国矿业大学学报, 2003, 32 (5) : 534-539. Huang Xinwu, Wu Lü, Niu Binhua. Reconstruction of Seismic Trace by Parabolic Radon Transform[J]. Journal of China University of Mining & Technology, 2003, 32 (5) : 534-539. |
| [10] | 王维红, 高红伟, 刘洪. 道均衡抛物线Radon变换法地震道重建[J]. 石油地球物理勘探, 2005, 40 (5) : 518-522. Wang Weihong, Gao Hongwei, Liu Hong. Seismic Trace Reconstruction by Trace Equalization Parabolic Radon Transform[J]. Oil Geophysical Prospecting, 2005, 40 (5) : 518-522. |
| [11] | 张军华, 吕宁, 雷凌, 等. 抛物线拉冬变换消除多次波的应用要素分析[J]. 石油地球物理勘探, 2004, 39 (4) : 398-405. Zhang Junhua, Lü Ning, Lei Ling, et al. Analysis of Applied Factors for Using Parabolic Radon Transform to Remove Multiple[J]. Oil Geophysical Prospecting, 2004, 39 (4) : 398-405. |
| [12] | 李晶晶, 孙成禹, 谢俊法, 等. 相对保幅的抛物线Radon变换法地震道重建[J]. 石油物探, 2014, 53 (2) : 181-187. Li Jingjing, Sun Chengyu, Xie Junfa, et al. Seismic Trace Reconstruction by Relative Amplitude-Preserved Parabolic Radon Transform[J]. Geophysical Prospecting for Petroleum, 2014, 53 (2) : 181-187. |
| [13] | 石颖, 张振, 李婷婷, 等. λ-f域加权抛物Radon变换地震数据重建方法研究[J]. 地球物理学进展, 2014, 29 (4) : 1752-1757. Shi Ying, Zhang Zhen, Li Tingting, et al. Investigation on Seismic Data Reconstruction by λ-f Domain Weighted Parabolic Radon Transform Method[J]. Progress in Geophysics, 2014, 29 (4) : 1752-1757. |
| [14] | Liu B, Sacchi M. Minimum Weighted Norm Inter-polation of Seismic Records[J]. Geophysics, 2004, 69 (6) : 1560-1568. DOI:10.1190/1.1836829 |
| [15] | Trad D. Five-Dimensional Interpolation:Recovering from Acquisition Constraints[J]. Geophysics, 2009, 74 (6) : V123-V132. DOI:10.1190/1.3245216 |
| [16] | Wang J, Wang S. Hybrid 5D Fourier Transform:A Flexible Tool for Land Data Interpolation[C]//SEG Annual Meeting. Houston:Society of Exploration Geophysicists, 2013:3603-3607. |
| [17] | 谢俊法, 孙成禹, 韩文功. 迭代抛物Radon变换法分离一次波与多次波[J]. 石油地球物理勘探, 2014, 49 (1) : 76-81. Xie Junfa, Sun Chengyu, Han Wengong. Iterative Parabolic Radon Transform for Primary and Multiple Separations[J]. Oil Geophysical Prospecting, 2014, 49 (1) : 76-81. |
| [18] | 王东凯.浅海OBC资料自由表面多次波压制方法研究[D].青岛:中国海洋大学, 2014. Wang Dongkai. Study on Surface-Related Multiples Attenuation of OBC Data in Shallow Water[D]. Qingdao:Ocean University of China, 2014. http://industry.wanfangdata.com.cn/sh/Detail/Thesis?id=Thesis_D548447 |
| [19] | 吕进英, 郭磊. 地震勘探中多次波的识别和压制[J]. 中州煤炭, 2011 (4) : 29-31. Lü Jinying, Guo Lei. Identification and Suppression of Multiple Waves in Seismic Exploration[J]. Zhongzhou Coal, 2011 (4) : 29-31. |
| [20] | Wang Y, Chang X, Hu H, et al. Simultaneous Re-verse Time Migration of Primaries and Free-Surface Related Multiples without Multiple Prediction[J]. Geophysics, 2013, 79 (1) : S1-S9. |
| [21] | Curry W, Shan G. , Interpolation of near Offsets Using Multiples and Prediction-Error Filters[J]. Geophysics, 2010, 75 (6) : WB153-WB164. DOI:10.1190/1.3506557 |
| [22] | Guo Shujuan, Li Zhenchun, Tong Zhaoqi, et al. Interpolation of Near Offset Using Surface-Related Multiples[J]. Applied Geophysics, 2011, 8 (3) : 225-232. DOI:10.1007/s11770-011-0284-2 |
| [23] | 郭书娟, 方伍宝, 徐兆涛. 基于表层多次波的地震数据插值方法研究[J]. 石油物探, 2013, 52 (6) : 636-641. Guo Shujuan, Fang Wubao, Xu Zhaotao. Interpolation of Near Offset Seismic Trace Using Surface-Related Multiples[J]. Geophysical Prospecting for Petroleum, 2013, 52 (6) : 636-641. |
| [24] | 郭书娟.表层多次波成像方法研究[D].青岛:中国石油大学(华东), 2012. Guo Shujuan. Seismic Imaging of Surface-Related Multiples[D]. Qingdao:China University of Petroleum (East China), 2012. |