2. 犹他大学矿产和地球科学学院, 美国 犹他州 盐湖城 84112
2. College of Mines & Earth Sciences, University of Utah, Salt Lake City 84112, UT, USA
0 引言
自从Tikhonov和Cagniard时代以来,大地电磁得到空前的发展,反演经历了两位学者时期的一维反演到70年代开始的二维反演,至今,三维地质结构的反演已成为主流。而在这一发展历程中,多数正反演数值方法均基于规则化网格[1-3]。目前常用的电磁数值方法包括有限单元法(FE)、有限差分法(FD)和积分方程法(IE)。积分方程法只需要对异常区域进行剖分,因而对于简单模型中有若干局部异常非常有效;同时,积分方程法不需要额外的边界条件。对于复杂几何形状的异常体,譬如地形起伏,积分方程法只能用阶梯状网格来近似,且该方法所形成的矩阵为满阵,因此当异常区域较大时,模拟效率会明显降低[4]。有限差分法相对而言较为简单,通过有限差分法形成的总体系数矩阵为稀疏矩阵,求解效率很高[5],可解决积分方程中模拟大型异常区域的困难。类似于积分方程法,有限差分法也只能用规则网格对模拟区域进行剖分,尤其是有限差分发展前期,矩形单元内的电导率、磁导率、介电常数往往设置为常数,对于复杂的几何形状,有限差分法只能用阶梯状网格来近似。Aprea等[6]将矩形单元细分为三角形单元以适应简单的倾斜地表及异常体;但对于弯曲的分界面,有限差分法的应用受到极大的限制。相比基于结构化网格的有限差分和积分方程法,基于非结构化网格的有限单元法更适合于复杂电阻率模型下的电磁模拟,其形成的总体系数矩阵的稀疏性与有限差分法相当,求解线性方程组的效率很高[7]。
由于有限单元法的自然边界条件在积分表达式中可自动得到满足,以能够模拟任意形状区域而著称,所以离散化技术对有限单元法的应用至关重要。一开始受到剖分技术的阻碍,有限单元法采用结构化网格进行数值模拟。结构化网格在拓扑结构上相当于矩形域内的均匀网格,节点定义在每一层网格线上,且每层的节点数目都是相等的。其生成速度快、数据结构简单,对曲面或空间的拟合大多数采用参数化或样条插值等方法获得,但对于复杂求解区域的网格化受到极大的限制。譬如模拟起伏地形时,可能会产生纵横比很大的矩形单元,从而导致方程组求解的收敛性差[8]。Fox等[9]以及Wannamaker等[10]引入矩形对角线将矩形细化为三角形,通过给不同三角形单元赋予不同的电磁参数以模拟倾斜异常体及起伏地表,这一方法在一定程度上增加了有限单元法网格剖分的灵活性和适应性。除了矩形和结构化三角形单元外,还发展了曲边四边形剖分技术[11],而且远不止于此,灵活性、适应性更强的非结构化网格也迅速发展起来。
非结构化三角形网格的优化策略一般采用后验误差估算算法[12]来保证获得最高质量的网格。后验误差估算算法的基本思路是根据后验误差值来决定网格是否需要加密,加密的方法主要有两种:一是根据三角形最长边的中点,将原三角形分为两个新的三角形;二是根据原来三角形三条边的中点将其细分为四个新的三角形。一般是这两种方法混合使用[12]。在三维模拟中,McFee等[13]利用非结构化四面体优化计算网格以获得高精度的解。此外,随着陆地电磁法理论的成熟,海洋大地电磁法、可控源海洋电磁法等也迅速发展起来。海底地形复杂多变及介质的各向异性使得传统规则化网格的应用受阻,非结构化网格为海洋电磁法数值模拟开辟了新思路和提供技术支撑[12, 14-16]。
由于非结构化网格优化程度高、适应性强而被逐渐引入电磁法数值模拟中,主流非结构化网格所采用的单元一般为三角形(2D)和四面体(3D)。本文研究非结构化四边形的剖分能力、适应性及对计算精度的影响等方面的内容。
1 伽辽金有限元方法取谐时变因子为eiωt, 在直角坐标系中,假设地质构造走向沿y轴无限延伸,根据Maxwell方程可得到TM、TE两组解耦合的电磁场模式满足的微分方程[17],将其带入Rodi[18]、陈乐寿[19]给出的边界条件,即可获得MT满足的边值问题。
本文采用非结构化四边形网格对模拟区域进行剖分。非结构化四边形网格的生成主要有推进波阵面法、递归分解法等。本文以推进波阵面法生成四边形网格,其主要思想是将多介质复杂区域分解为若干由单一介质组成的子域,每一子域单独生成网格,由各子域的网格合并构成区域的网格。子域网格生成顺序是从边界到区域内部,即取子域的全部边界节点作为初始生成波,并在生成波上选取一边作为底边,在区域内生成一个四边形单元。随着单元的生成,生成波不断更新,向区域内推进,并利用背景网格控制网格的疏密,从而达到自适应目的[20-21]。图 1为非结构化四边形网格示意图。相较于结构化网格而言,非结构化网格没有规则的拓扑结构,也没有层的概念,具有网格大小和节点密度容易控制、采用随机数据结构有利于进行网格自适应等优点。

|
| 图 1 自由四边形网格示意图 Figure 1 Schematic diagram of free quadrilateral meshes |
|
|
模拟区域离散化之后,根据伽辽金有限元法[22],即可获得网格各节点的电场或者磁场值。尔后,针对起伏地形求解辅助场与水平地表的差异,根据Lee等[17]的方法即可获得地下介质的电阻率分布信息。
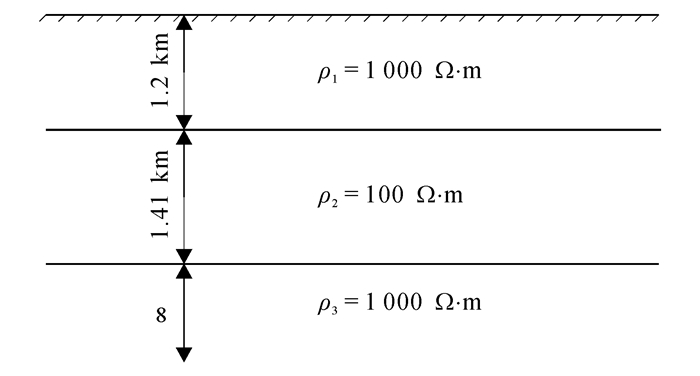
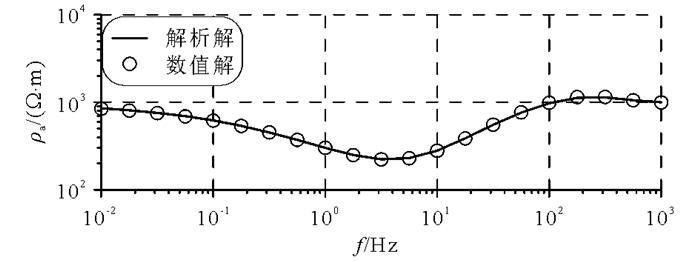
2 算例分析 2.1 算法有效性验证为了验证本文方法的有效性,首先计算水平层状介质模型响应并与解析解对比。构建一个H型地电模型(图 2),采用非结构化自由四边形网格剖分,正演结果如图 3所示。从图 3可知,数值解和解析解吻合情况令人满意,平均相对误差小于0.5%。
|
| ρa为视电阻率;f为计算频率。 图 2 H型地电模型 Figure 2 H type geoelectric model |
|
|
|
| 图 3 水平层状介质数值解与解析解对比 Figure 3 Comparison between numerical solution and analytic solution of layered media |
|
|
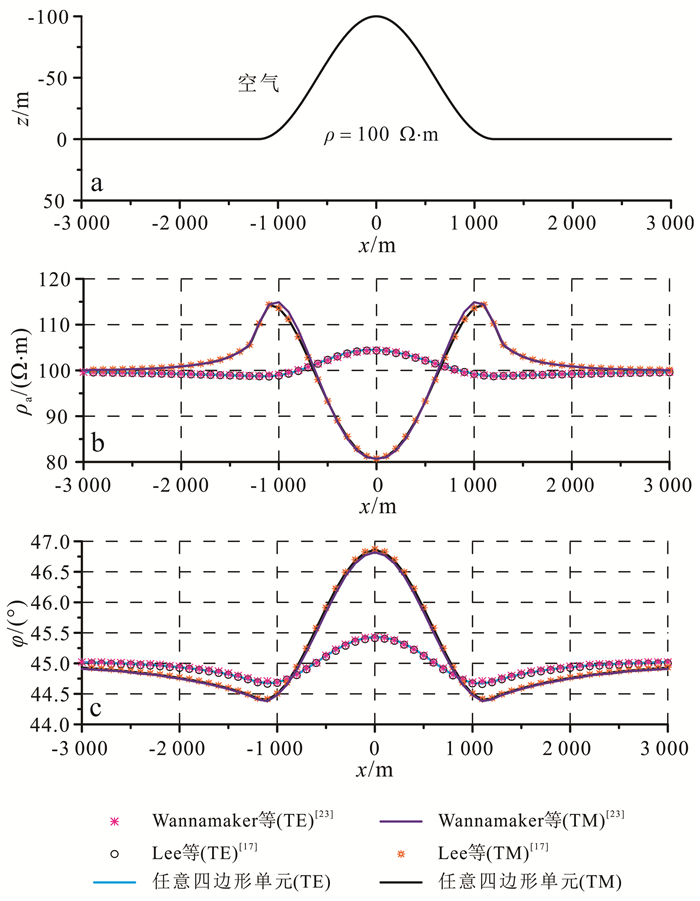
为了测试算法对地形的适应性以及进一步验证算法的有效性,对山脊地形模型[17, 23]进行试算,并与前人的数值解对比。山脊地形如图 4a所示,山脚相距2.4 km、高0.1 km,电阻率为100 Ω·m。以下是其他学者对计算区域的剖分方式。Lee等[17]根据地表上任意位置的高程,通过插值计算获取地表网格节点的高程,并利用地表网格节点的高程来移动矩形网格节点的z坐标;此时,矩形网格转变成任意四边形网格,并且要使得网格节点z坐标的变化量从地表向上(TE模式)、下(TE、TM模式)边界递减以保证水平边界条件得以应用。他们方法的不足之处在于,地下异常体的形状会随着网格的变形而改变,而且不便于构建任意形状的异常体。Wannamaker等[23]将矩形单元细分为四个三角单元,根据余弦函数确定矩形的宽度和高度。虽然结构化三角形相较矩形具有一定的优势,但是对于更为复杂的地形及异常区域,其缺陷是显而易见的。因此,本文直接采用COMSOL Multiphysics软件的内部函数,以半周期余弦函数生成山脊地形,并用非结构化自由四边形网格离散计算区域。
取与文献[17, 23]相同的计算频率10 Hz。如图 4b、c所示,地形对大地电磁场的扰动是明显的。从图 4b可知,地形对TM模式视电阻率的影响远大于TE模式,TM模式视电阻率异常幅值(视电阻率最大值/视电阻率最小值)为1.41,而TE模式视电阻率异常幅值为1.06。此外,从图 4b、c中还可以发现:TE模式视电阻率曲线形态与相位曲线形态相似,也与地形形态相似;而TM模式视电阻率曲线形态与相位曲线形态近似于相反,其几乎与地形成镜像关系,TM模式的这种现象与地形对直流电场视电阻率的畸变非常类似。通过提取Wannamaker等[23]及Lee等[17]文献中的图件数据并与本文结果对比可知,三者的规律吻合。
|
| a.山脊地形模型;b.视电阻率曲线;c.相位曲线。f=10 Hz。 图 4 山脊地形模型MT响应 Figure 4 MT responses of a hill model |
|
|
以上两个算例结果说明了本文算法的有效性。实际区域构造远比上述模型复杂。为了认识复杂地质构造对天然电磁场的频率响应,设计了断层构造模型、起伏地形与低阻椭球体模型和褶皱构造模型,并计算它们的响应。
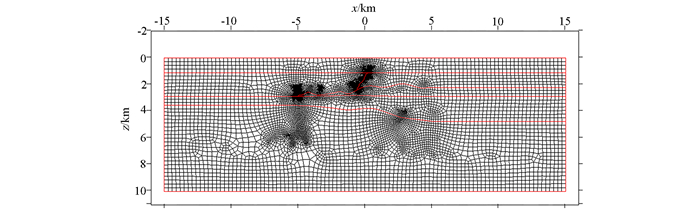
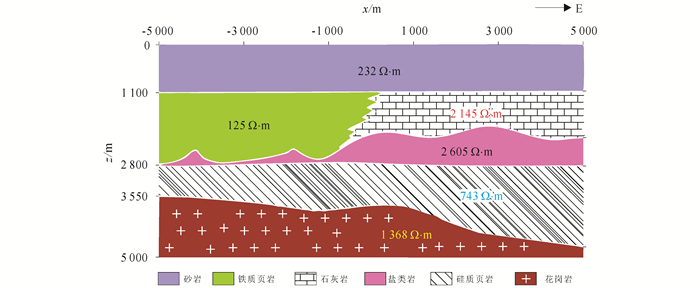
2.2 断层构造模型图 5为断层构造模型TM模式的剖分示意图,剖面纵、横范围分别是0~10 km和-15~15 km,网格单元数为13 380,节点数为13 523。TE模式计算区域空气层厚度为10 km,网格单元数为17 485,节点数为17 657。为了便于观察模型区域中较复杂的构造(纵向:0~5 km,横向:-5~5 km),将其单独展示,如图 6所示。岩石电阻率取测试样本中的均值[24]。对于如图 6所示的断层构造模型,无论是矩形网格还是结构化的三角形及四边形网格都难以模拟,而本文方法很容易实现,这也体现了非结构化网格具有结构化网格无法比拟的优势。
|
| 图 5 断层构造模型TM模式非结构化网格化示意图 Figure 5 Unstructured meshes for the fault model |
|
|
|
| 图 6 断层构造模型 Figure 6 The fault model |
|
|
沿测线布设41个测点,起始点位于-10 km处,点距为500 m;计算频率取10-3~103Hz,按对数等间隔共截取21个频点,断层构造模型正演响应如图 7所示。
|
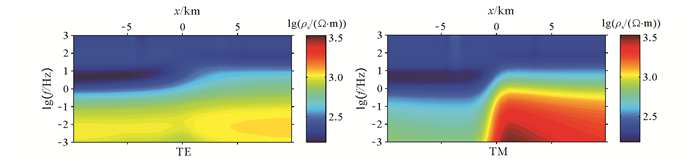
| 图 7 断层构造模型视电阻率拟断面图 Figure 7 Apparent resistivity pseudosection of the fault model |
|
|
从图 7可知,地下电性结构在正演响应中得到了较好的体现:1) TE、TM模式均反映出了浅部低阻砂岩覆盖层异常,同时可以观察到覆盖层之下的断裂带,其倾向向西,断裂带上盘为低阻铁质页岩异常,下盘为高阻灰岩异常;2) 对于基底及其之上的两层岩石的电性异常特征,TE、TM模式具有较大的差异;对TE模式而言,由于真实模型的电阻率差异不大,另外,视电阻率只是地形起伏以及各种岩石电阻率的一种综合反映,因而仅能大致呈现出分层特征;对于TM模式,根据其纵向分辨率低的特性推测,西侧低阻异常可能由低阻铁质页岩造成。
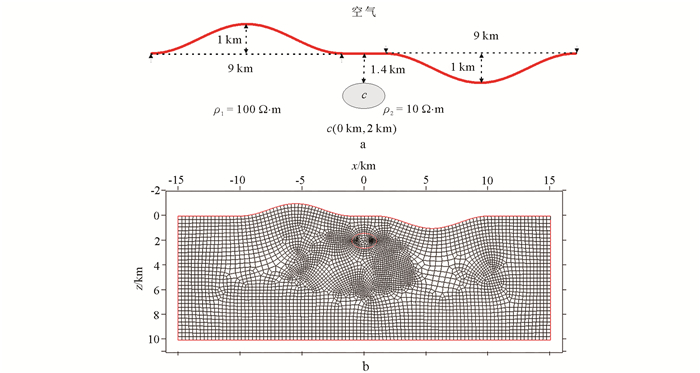
2.3 起伏地形与低阻椭球体模型图 8a为起伏地形与低阻椭球体模型示意图。围岩电阻率为100 Ω·m;椭球体(c)电阻为10 Ω·m,半长轴为1 km,半短轴为0.6 km,中心坐标为(0 km, 2 km);山脊和山谷的跨度均为9 km,高度分别为1 km和-1 km,连接二者的水平地表长度为2 km,坡度按照半周期余弦函数变化。起伏地形与低阻椭球体模型TM模式网格化示意图如图 8b所示,网格单元数为5 053,节点数为5 191。TE模式计算区域空气层厚度为10 km,网格单元数为9 239,节点数为9 408。测点及频率信息同算例2.2。
|
| a.模型示意图;b.网格化示意图。 图 8 起伏地形与低阻椭球体模型TM模式非结构化网格化示意图。 Figure 8 Unstructured meshes for a conductived ellipse beneath rugged topography in TM mode |
|
|
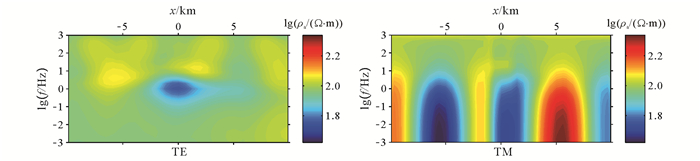
图 9显示地形起伏造成电磁场剧烈扰动,尤其是TM模式。假设地球为无磁性介质,在TM模式中,沿走向的地表磁场值为常数,因此TM模式的畸变受电场畸变的控制。在地形水平时,地下为均匀水平电流场,电流线为水平线,电流密度处处相等;当存在地形起伏时,山脊区电流密度降低,视电阻率减小,山谷区电流密度增加,视电阻率增大。因而,TM模式在山脊和山谷之下分别呈现低阻异常和高阻异常,剖面中心的低阻异常为低阻体引起的。相较而言,TE模式的畸变同时受电场和磁场畸变的控制,受地形影响较弱;当地形起伏幅度小于电磁波的趋肤深度时,TE模式的畸变将会逐渐消失[25-26]。
|
| 图 9 起伏地形与低阻椭球体模型视电阻率拟断面图 Figure 9 Apparent resistivity pseudosection of a conductived ellipse beneath rugged topography |
|
|
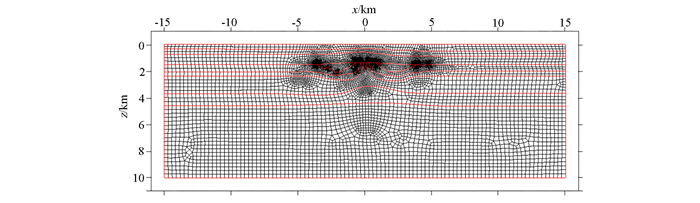
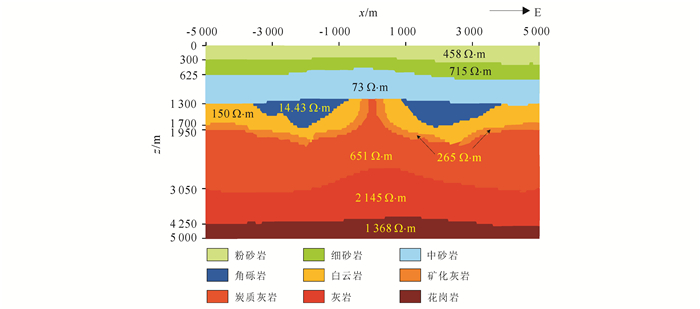
图 10为褶皱构造模型的TM模式网格剖分示意图,单元数为35 120,节点数为35 524。TE模式空气层厚度为10 km,网格单元数为68 326,节点数为68 830。与算例2.2相同,将模型区域构造复杂的部分单独展示,如图 11所示(纵向:0~5 km,横向:-5~5 km),地层分界线清晰可见。按照地层运动规律推断,地表之下三层砂岩为晚期形成的覆盖层;它们之下的地层应该是遭受横向挤压,引发褶皱构造,向斜被角砾岩填充,背斜遭遇风化剥蚀削平。
|
| 图 10 褶皱构造模型TM模式非结构化网格化示意图 Figure 10 Unstructuredmeshes for the folded model in TM model |
|
|
|
| 图 11 褶皱构造模型 Figure 11 The folded model |
|
|
测点及频率信息同算例2.2。
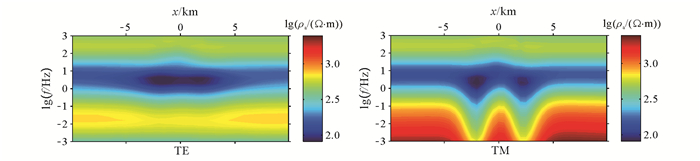
从褶皱构造模型的正演结果(图 12)来看,异常的分布具有显著的分层现象,由于两低阻角砾岩填充体的存在,映现出两低阻异常。同时可以观察到,TE模式横向分辨率不足致使两低阻异常衔接为一体,而TM模式纵向分辨率不足导致向下延伸异常带的出现。
|
| 图 12 褶皱构造模型视电阻率拟断面图 Figure 12 Apparent resistivity pseudosection of the folded model |
|
|
本文讨论了基于非结构化四边形网格的大地电磁有限元二维数值模拟,得出以下两点结论。
1) 算法有效性验证算例表明,基于非结构化四边形网格的MT二维正演具有与解析解及前人数值解相当的精度,并更便于模拟起伏地形。复杂地质模型的算例证明,非结构化四边形网格能够适应复杂的地电模型,使正演模型更具实际地质构造的意义,有助于人们对野外视电阻率数据的进一步认识。
2) TE模式响应受地形影响较弱,而TM模式响应受地形干扰较为严重。TM模式在山脊处出现低阻异常,在山谷处出现高阻异常;而对TE模式而言,当地形起伏幅值小于趋肤深度时,地形影响逐渐消失。再者,TE模式纵向分辨率优于横向分辨率,TM模式则相反。
| [1] | 赵广茂, 李桐林, 王大勇, 等. 基于二次场二维起伏地形MT有限元数值模拟[J]. 吉林大学学报(地球科学版), 2008, 38 (6) : 1055-1059. Zhao Guangmao, Li Tonglin, Wang Dayong, et al. Secondary Field-Based Two-Dimensional Topographic Numerical Simulation in Magnetotellurics by Finite Element Method[J]. Journal of Jilin University (Earth Science Edition), 2008, 38 (6) : 1055-1059. |
| [2] | 顾观文, 吴文鹂, 李桐林. 大地电磁场三维地形影响的矢量有限元数值模拟[J]. 吉林大学学报(地球科学版), 2014, 44 (5) : 1678-1686. Gu Guanwen, Wu Wenli, Li Tonglin. Modeling for the Effect of Magnetotelluric 3D Topography Based on the Vector Finite-Element Method[J]. Journal of Jilin University (Earth Science Edition), 2014, 44 (5) : 1678-1686. |
| [3] | 李桐林, 张镕哲, 朴英哲. 大地电磁测深与地震初至波走时交叉梯度反演[J]. 吉林大学学报(地球科学版), 2015, 45 (3) : 952-961. Li Tonglin, Zhang Rongzhe, Pak Yongchol. Joint Inversion of Magnetotelluric and First-Arrival Wave Seismic Traveltime with Cross-Gradient Constraints[J]. Journal of Jilin University (Earth Science Edition), 2015, 45 (3) : 952-961. |
| [4] | Zhdanov M S, Lee S K, Yoshioka K. Integral Equa-tion Method for 3D Modeling of Electromagnetic Fields in Complex Structures with Inhomogeneous Background Conductivity[J]. Geophysics, 2006, 71 (6) : 333-345. DOI:10.1190/1.2358403 |
| [5] | Newman G A, Alumbaugh D L. Frequency-Domain Modelling of Airborne Electromagnetic Responses Using Staggered Finite Differences[J]. Geophysical Prospecting, 1995, 43 (8) : 1021-1042. DOI:10.1111/gpr.1995.43.issue-8 |
| [6] | Aprea C, Booker J R, Smith J T. The Forward Pro-blem of Electromagnetic Induction:Accurate Finite-Difference Approximations for Two Dimensional Discrete Boundaries with Arbitrary Geometry[J]. Geophys J Int, 1997, 129 (1) : 29-40. DOI:10.1111/gji.1997.129.issue-1 |
| [7] | Cai H Z, Xiong B, Han M, et al. 3D Controlled-Source Electromagnetic Modeling in Anisotropic Medium Using Edge-Based Finite Element Method[J]. Computers & Geosciences, 2014, 73 : 164-176. |
| [8] | Key K, Weiss C. Adaptive Finite-Element Modeling Using Unstructured Grids:The 2D Magnetotelluric Example[J]. Geophysics, 2006, 71 (6) : G291-G299. DOI:10.1190/1.2348091 |
| [9] | Fox R C, Hohmann G W, Killpack T J, et al. Topo-graphic Effects in Resistivity and Induced-Polarization Surveys[J]. Geophysics, 1980, 45 (1) : 75-93. DOI:10.1190/1.1441041 |
| [10] | Wannamaker P E, Stodt J A, Rijo L. A Stable Finite Element Solution for Two-Dimensional Magneto-telluric Modelling[J]. Geophys J Int, 1987, 88 (1) : 277-296. DOI:10.1111/j.1365-246X.1987.tb01380.x |
| [11] | Reddy I K, Rankin D. Magnetotelluric Response of Laterally Inhomogeneous and Anisotropic Media[J]. Geophysics, 1975, 40 (6) : 1035-1045. DOI:10.1190/1.1440579 |
| [12] | Franke A, Börner R U, Spitzer K. Adaptive Unstru-ctured Grid Finite Element Simulation of Two-Dimensional Magnetotelluric Fields for Arbitrary Surface and Seafloor Topography[J]. Geophys J Int, 2007, 171 (1) : 71-86. DOI:10.1111/gji.2007.171.issue-1 |
| [13] | McFee S, Giannacopoulos D. Optimal Discretizations in Adaptive Finite Element Electromagnetics[J]. Int J Numer Methods Eng, 2001, 52 (9) : 939-978. DOI:10.1002/nme.240 |
| [14] | Badea E A, Everett M E, Newman G A, et al. Finite-Element Analysis of Controlled-Source Electro-magnetic Induction Using Coulomb-Gauged Potentials[J]. Geophysics, 2001, 66 (3) : 786-799. DOI:10.1190/1.1444968 |
| [15] | Li Y, Pek J. Adaptive Finite Element Modelling of Two-Dimensional Magnetotelluric Fields in General Anisotropic Media[J]. Geophys J Int, 2008, 175 (3) : 942-954. DOI:10.1111/gji.2008.175.issue-3 |
| [16] | Puzyrev V, Koldan J, Puente J, et al. A Parallel Finite-Element Method for Three-Dimensional Controlled-Source Electromagnetic Forward Modelling[J]. Geophys J Int, 2013, 193 (2) : 678-693. DOI:10.1093/gji/ggt027 |
| [17] | Lee S K, Kim H J, Song Y, et al. MT2D Inv Matlab:A Program in MATLAB and FORTRAN for Two-Dimensional Magnetotelluric Inversion[J]. Computers & Geosciences, 2009, 35 (8) : 1722-1734. |
| [18] | Rodi W L. A Technique for Improving the Accuracy of Finite Element Solutions for Magnetotelluric Data[J]. Geophys J Int, 1976, 44 (2) : 483-506. DOI:10.1111/j.1365-246X.1976.tb03669.x |
| [19] | 陈乐寿. 有限元法在大地电磁场正演计算中的应用及改进[J]. 石油勘探, 1981 (3) : 84-103. Chen Leshou. Application and Improvement of Finite Element Method in Forward Calculation of Geo-Electromagnetic Field[J]. Geophysical Prospecting for Petroleum, 1981 (3) : 84-103. |
| [20] | 邓建辉, 熊文林, 葛修润. 复杂区域非结构化四边形网格全自动生成方法[J]. 计算结构力学及应用, 1995, 12 (2) : 196-204. Deng Jianhui, Xiong Wenlin, Ge Xiurun. Automatic Generation of Unstructured Quadrilateral Mesh for Complex Domain[J]. Computational Structural Mechanics and Application, 1995, 12 (2) : 196-204. |
| [21] | 陈建军, 郑耀, 陈立岗, 等. 非结构化四边形网格生成新算法[J]. 中国图像图形学报, 2008, 13 (9) : 1796-1803. Chen Jianjun, Zheng Yao, Chen Ligang, et al. A New Unstructured Quadrilateral Mesh Generation Algorithm[J]. Journal of Image and Graphics, 2008, 13 (9) : 1796-1803. |
| [22] | Jin J M. The Finite Element Method in Electroma-gnetics[M]. New Jersey: Wiley-IEEE Press, 2002: 1-780. |
| [23] | Wannamaker P E, Stodt J A, Rijo L. Two-Dimen-sional Topographic Responses in Magnetotellurics Modeled Using Finite Elements[J]. Geophysics, 1986, 51 (11) : 2131-2144. DOI:10.1190/1.1442065 |
| [24] | 李磊. 湘南骑田岭锡铅锌多金属矿区岩矿石电性研究[J]. 物探与化探, 2007, 31 (增刊 1) : 77-80. Li Lei. Researches on Rock Electrical Properties in the Qitianling Tin, Lead and Zinc Polymetallic Ore Deposit, Southern Hunan[J]. Geophysical and Geochemical Exploration, 2007, 31 (Sup. 1) : 77-80. |
| [25] | Chouteau M, Bouchard K. Two-Dimensional Terrain Correction in Magnetotelluric Surveys[J]. Geophysics, 1988, 53 (6) : 854-862. DOI:10.1190/1.1442520 |
| [26] | Jiracek G R. Near-Surface and Topographic Distor-tions in Electromagnetic Induction[J]. Surveys in Geophysics, 1990, 11 : 163-203. DOI:10.1007/BF01901659 |



