2. 北京科技大学土木与资源工程学院, 北京 100083;
3. 山东黄金(北京)产业投资有限公司矿业基金部, 北京 100029;
4. 长春黄金设计院, 长春 130000;
5. 中铁资源集团有限公司金属事业部, 北京 100039
2. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China;
3. Mining Funds Department of Shandong Gold (Beijing) Industrial Investment Co., Ltd, Beijing 100029, China;
4. Changchun Gold Design Institute, Changchun 130000, China;
5. Metal Project Department, China Railway Resources Group Co. Ltd, Beijing 100039, China
0 引言
矿产资源储量是国家和地方合理规划工业布局,优化市场资源配置,制定国民经济计划与资源政策的重要依据;也是安排矿产勘查计划,衡量矿床潜在经济价值,矿山开发建设与生产计划和管理的重要依据。因此,在矿产勘查、矿山设计、生产及管理等各阶段都需要进行资源储量估算的工作。
在长期的生产实践中,地质、采矿工作者形成了一系列资源储量估算方法,取得了巨大的成就。目前,我国常用的资源储量估算方法有4种:传统几何法、距离幂次反比法、地质统计学法、SD法。其中,地质统计学法由于能最大限度地利用勘探工程所获得的各种信息,所以估算精度高,可以避免系统误差。另外,该方法便于与计算机结合,在资源储量估算中正发挥着越来越重要的作用[1-5]。
将三维建模技术与储量计算结合起来是当前矿产资源储量计算的一个新的发展方向,它可以更加直观、准确地对矿产储量进行计算[6]。基于体模型的建模方法可以表达、分析三维地质体的内部属性[7]。该方法是将地质体内空间进行剖分[8],并用规则或不规则几何体进行填充的一种建模方式。目前,我国矿业领域广泛应用的主流矿业软件3DMine、Micromine、Surpac[9]等均采用规则正六面体为基本单元进行三维空间划分。
基于块模型的资源储量估算是根据一定的精度要求,将矿体离散为有限的三维体元,并以体元的中心点作为该体元属性值的位置参考点,利用采集到的样品信息,对所有体元的中心点进行插值运算,表征矿体内部的物理化学属性,从而完成矿体内部的属性信息建模[10]。在此过程中,块尺寸选择合理与否对资源储量估算结果至关重要。
在地质勘探阶段,由于没有进行资源开采可行性研究,对资源的利用方式还不是很明确,一般认为单元块大小主要根据地质勘探网度确定。北京大学孙玉建[11]指出合理确定块尺寸需要综合考虑地质特征、勘查程度、开采方法、设备选型、条件模拟五方面因素。中国恩菲工程技术有限公司赵战锋等[12]认为地质建模过程中设定矿块尺寸需要考虑矿体形态、钻孔网度、变程和采矿方法等多种因素。
在矿山生产阶段,块尺寸同样影响资源储量估算的结果,单元块大小主要取决于最小可采单元。程志刚[13]研究了德兴铜矿矿床工业指标与矿块大小的关系,提出矿块大小对储量估算影响显著。南昌有色冶金设计院司永年[14]研究了德兴铜矿分采单元规格与出矿品位及开采成本的关系,为生产矿山选择合适的分采单元提供了参考。北京科技大学陈希廉教授[15]进一步明确指出矿体三维模型中单元块即为允许分采的最小单元。
矿床处于不同开发阶段,其资源储量估算中块尺寸的选择依据也不同。本文从理论分析及实例分析两方面讨论了块尺寸与品位、储量、估计方差、选别开采单元之间的关系,为地质统计学资源储量估算中块尺寸的合理选择提供参考。
1 块尺寸对品位估计精度的影响采用地质统计学法进行资源储量估算,其实质是利用区域化变量的已知数据和变异函数的结构特点,对未知样点进行线性、无偏、最优估计。
在地质统计学资源储量估算过程中,三维矿业软件通常以矿床有价元素品位作为区域化变量,将离散单元块作为待估块,钻孔组合样或刻槽组合样等作为信息样品。用于表征品位估计精度的主要参数有估计方差和离差方差。
1.1 估计方差对于任一待估块段V的真实值Z的估计值ZV*是通过该待估块段影响范围内n个有效样品值Z(xi)(i=1,2,…,n)的线性组合得到的,
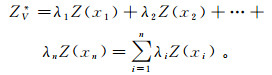
式中:λi是加权因子,是各样品在估计ZV*时的影响大小,而估计方法的好坏就取决于如何计算或选择加权因子λi。其估计误差的方差存在,且为σ2=E(ZV-ZV*)2。我们期望估计值的均值与实际值相同,即:

而且,希望估计的误差尽量小些,即:
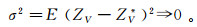
如果Z(xi)满足二阶平稳假设,经推导,克里格估计方差为

式中:γ-(V, vi)为已知信息域vi和待估块段V间的平均变异函数;γ-(V, V)为待估块段本身平均变异函数;γ-(vi, vj)为已知信息域vi和vj间的平均变异函数;n为样品点数。
可见,影响估计方差的主要因素有以下几种:
1)信息样品v的几何特征、数量及构形。
2)待估块体V和信息样品v之间的距离、方位及构形。
3)变差函数或协方差函数,变差函数是反映矿化结构性和随机性总特征的结构函数。
4)待估块体V的大小与形状等几何特征。
理论上,给定一组信息样品,存在着某个特定的单元块尺寸使地质统计学估值的估计方差最小。一般而言,仅以估计方差最小为依据所确定的最优块尺寸要比能够被接受的可精确表达地质边界的块尺寸大得多[16]。
因此,在可接受的块尺寸范围内,待估块尺寸越小估计方差越大,资源储量估值精度越低。为保证估值精度,应适当选择较大的块尺寸。
1.2 离差方差若V是以点x为中心的开采面,将其分成以xi为中心的N个大小相等的单元v(xi)(i=1, 2, ..., N),则有:
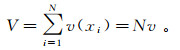
再把v离散成若干个点y,其品位为Z(y),则每个以点xi为中心的单元v(xi)的平均品位是:
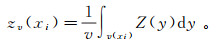
以x为中心的开采面V的平均品位是:
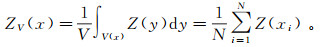
显然,这N个品位值zv(xi)(i=1, 2, ..., N)对它的平均值ZV(x)的离散程度可用其方差表示:
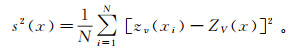
当x固定,则zv(xi)与ZV(x)均为随机变量,因而s2(x)也是一个随机变量,从而可以讨论它的数学期望。在区域化变量Z(y)满足二阶平稳假设条件下,把随机变量s2(x)的数学期望定义为在开采面V内N个生产单元v的离差方差:

s2(x)为实验方差。在二阶平稳条件下,s2(x)的平稳数学期望就是开采单元对生产块段的离散方差。当v和N的数量无限增加时,s2(x)趋向于离散方差D2(v/V)。经推导得到离差方差的通式:

或者用变异函数表示为
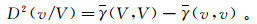
可见,以生产单元v来估计开采面V,估计的离差方差同样受块尺度影响。在其他条件相同的情况下,生产单元块尺度v越小离差方差越大,估计精度越低。换言之,相对同一开采面而言生产单元越小,品位波动越显著。
品位波动不利于生产的组织,还会增加矿石选别开采成本。因此,从经济角度考虑,应适当选择较大的块尺寸。
2 块尺寸对估值品位-吨位的影响在矿产资源储量估算工业指标的选择上,国内习惯于采用双指标体系[17-18],西方国家普遍采用单指标体系。以克里格法为理论基础,以块体模型为实现手段的资源储量估算适用于单指标体系。单指标体系用边际品位(cut-off grade)区分矿岩,该指标所对应的评价块尺寸不同,其评价结果相差明显。
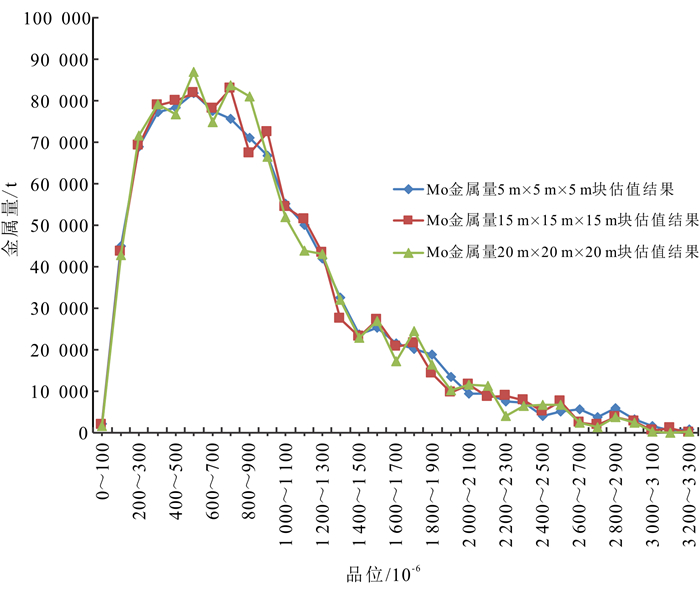
为了说明矿床品位-吨位与块体模型单元块尺寸的关系,以黑龙江省某特大型斑岩钼矿为例,采用相同的钻孔组合样数据、估值参数、搜索椭球,不同的块尺寸进行资源储量估算。
在Surpac软件平台下,设定实验块体尺寸分别为:5 m×5 m×5 m、15 m×15 m×15 m、20 m×20 m×20 m。3种不同块尺寸的估值结果显示矿体内总金属量接近,均为100.9万t;矿体体积分别为65 336万m3、65 339万m3、65 332万m3,与矿体实体模型体积65 340万m3接近;钼金属平均品位分别为569.8×10-6、569.9×10-6、570.0×10-6,该结果与钻孔组合样平均品位588.3×10-6接近。不同块尺寸对资源估算结果影响的对比如表 1所示。
| 品位区间/ 10-6 |
不同品位区间资源量所占比例/% | ||
| 块尺寸5 m× 5 m×5 m |
块尺寸15 m× 15 m×15 m |
块尺寸20 m× 20 m×20 m |
|
| 0~200 | 4.668 | 4.500 | 4.373 |
| 200~400 | 14.487 | 14.686 | 14.933 |
| 400~600 | 15.867 | 16.026 | 16.222 |
| 600~800 | 15.185 | 15.945 | 15.699 |
| 800~1 000 | 13.647 | 13.828 | 14.632 |
| 1 000~1 200 | 10.398 | 10.455 | 9.479 |
| 1 200~1 400 | 7.366 | 7.002 | 7.446 |
| 1 400~1 600 | 4.845 | 4.994 | 4.910 |
| 1 600~1 800 | 4.121 | 4.186 | 4.111 |
| 1 800~2 000 | 3.177 | 2.354 | 2.623 |
| 2 000~2 200 | 1.833 | 1.964 | 2.266 |
| 2 200~2 400 | 1.443 | 1.633 | 1.023 |
| 2 400~2 600 | 0.873 | 1.241 | 1.308 |
| 2 600~2 800 | 0.932 | 0.412 | 0.352 |
| 2 800~3 000 | 0.889 | 0.619 | 0.597 |
| 3 000~3 200 | 0.190 | 0.151 | 0.019 |
| 3 200以上 | 0.081 | 0.003 | 0.007 |
对不同品位区间段的钼金属量进行计算,并绘制品位分布曲线,如图 1所示。
|
| 图 1 钼金属品位分布曲线 Figure 1 Molybdenum grade distribution curve |
|
|
通过以上图表分析可知,在一定范围内改变块体尺寸,资源储量估算总体结果相近,但会影响矿体品位分布。品位分布对于矿床开采成本、贫化损失率控制、采掘计划的编排等都有重大影响。同一矿床,选择的块尺寸越小,单元块可达到的最高品位越高,相同边际品位条件下,可采矿石的平均品位越高。
进一步增大块尺寸,估值结果产生了较大波动。当块尺寸为45 m×45 m×45 m时,总金属量估算结果约为76.7万t,平均品位为545.2×10-6,块体模型中没有钼品位大于2 800×10-6的单元块出现,估值品位向低品位段集中,呈现贫化、均化的特点。此时,该矿床钼金属品位-吨位情况如表 2所示。
| 品位区间/ 10-6 |
吨位/ 万t |
Mo品位/ 10-6 |
Mo金属量/ t |
占比/ % |
| 0~200 | 21 682 | 88.3 | 763.2 | 0.099 |
| 200~400 | 44 698 | 248.8 | 63 467.7 | 8.273 |
| 400~600 | 25 707 | 450.2 | 62 700.0 | 8.173 |
| 600~800 | 20 176 | 650.3 | 68 891.1 | 8.980 |
| 800~1 000 | 11 829 | 844.6 | 48 386.3 | 6.307 |
| 1 000~1 200 | 7 013 | 1 046.1 | 45 724.8 | 5.960 |
| 1 200~1 400 | 3 507 | 1 244.6 | 25 203.7 | 3.285 |
| 1 400~1 600 | 2 420 | 1 449.0 | 14 671.2 | 1.912 |
| 1 600~1 800 | 1 902 | 1 640.5 | 11 748.4 | 1.531 |
| 1 800~2 000 | 716 | 1 857.1 | 7 796.4 | 1.016 |
| 2 000~2 200 | 321 | 2 054.3 | 3 043.8 | 0.397 |
| 2 200~2 400 | 420 | 2 252.6 | 2 781.4 | 0.363 |
| 2 400~2 600 | 272 | 2 417.5 | 2 388.0 | 0.311 |
| 2 600~2 800 | 49 | 2 616.0 | 1 292.0 | 0.168 |
| 总计 | 140 711 | 545.2 (均值) |
767 166.0 | 100 |
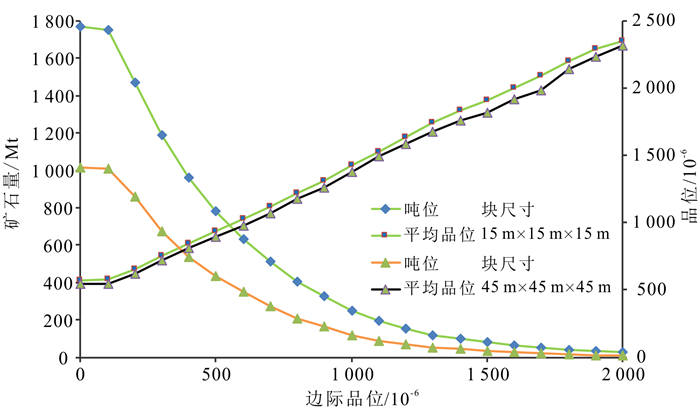
过大的块尺寸导致矿体边界的拟合精度下降,采用15 m×15 m×15 m的单元块与45 m×45 m×45 m的单元块估算的矿石量结果相差悬殊。至于何为过大的块尺寸,要视矿体形态、产状、尺寸而定,在资源储量估算过程中应尽量避免由此带来的误差。两种不同块尺寸品位-吨位曲线比较如图 2所示。
|
| 图 2 钼金属品位-吨位曲线对比图 Figure 2 Molybdenum grade-tonnage curve |
|
|
可见,块尺寸的选择对资源储量估算的结果有显著影响:块尺寸设置过大,边界拟合精度下降;块尺寸设置过小,估计精度下降。地质统计学资源储量估算中块尺寸不仅影响矿床品位分布,而且影响矿床平均品位及矿石量。实际操作中,应从边界拟合精度和估计精度两方面综合考量。推荐该矿床选择不超过45 m×45 m×45 m的单元块尺寸进行储量估算。
3 块尺寸与选别开采单元在矿山生产阶段,理论上要求块尺寸的大小与选别开采单元(selective mining unit,简称SMU)一致,这样采出矿量与储量估算结果才更接近。因此,从矿床开采角度来讲,影响资源储量估算中块尺寸的合理选择问题即为选别开采单元的确定问题。矿床露天开采和地下开采,选别开采单元的确定略有差别。限于篇幅,本文仅以露天矿为例来说明选别开采单元的确定问题。
影响露天矿选别开采单元确定的因素很多,可以分为地质因素、技术因素和经济因素。矿床地质特征是选别开采单元确定的决定性因素;矿床开采技术参数是实现选别开采的技术保障;矿床开采经济效益是选别开采单元合理与否的判别标准。
3.1 矿床地质特征矿床的地质特征决定了采矿方法和采矿参数,从而决定了选别开采单元的尺寸。在克里格法中,将地质特征以矿化域和变异函数为主要工具进行表述,矿化域限定已知样品点对待估区域的影响边界,而变异函数表示已知样品点对待估区域的影响程度。资源储量估算结果是否合理、准确,取决于研究人员对矿床地质特征的理解、运用程度。
影响选别开采的地质特征主要包括矿体的大小、产状、矿床的构造、水文地质条件、品位分布特征、矿石可选性等。显然,厚大稳定构造简单的矿床更适合选择较大的块尺寸进行开采。反之,为更好地适应矿床的空间变异性应选择较小的块尺寸。对于规模小而且形态复杂的矿体,不适合应用地质统计学方法进行块体建模及储量估算。
3.2 矿床开采技术参数露天矿开采台阶高度决定了选别开采单元的垂向尺寸。台阶高度直接影响穿孔、采装、运输设备的选择,而且与工作帮坡角、工作面推进速度、矿山工程的下降速度、生产剥采比均衡、生产成本等有关,是影响选别开采单元选择的一项关键技术指标。增加台阶高度有利于采掘设备效率的发挥,降低台阶高度有利于减小矿石损失与贫化。一般而言,大型露天矿选择较大的台阶高度,中小矿山选择较小的台阶高度。
铲装、运输设备的尺寸也是影响选别开采单元的重要因素,如铲斗尺寸、运输车辆装载量,均为设置合理的块尺寸提供了参考。我国大型露天矿铲斗容积一般为8~16 m3,考虑到矿体产状等因素,对应的最小可分采单元尺寸为4~8 m。
此外,对于矿岩界限不明显的品位渐变型矿床,地质勘探钻孔密度往往不足以进行生产品位控制,通常需要补充生产勘探及炮孔取样。炮孔取样密度决定了矿岩界限划分的可能性,因而影响选别开采单元的尺寸。
3.3 矿床开采经济效益在矿岩交界处,选别开采单元规格大则开采贫化(损失)大,分采单元规格小则生产成本高,贫损指标与生产成本控制是一对矛盾。由于矿体地质特征和矿床开采技术参数的不同,不同矿山选别开采单元与开采成本及收益间的关系也是不同的。通过对选别开采单元的尺度与开采成本的关系研究,可以得出矿岩平均收益表达式,进而以经济效益为判别依据选择最佳选别开采单元尺寸。
综合分析,推荐该矿床选择15 m×15 m×15 m的单元块尺寸进行储量估算。
4 结论本文从理论及实践两个方面深入探讨了地质统计学资源储量估算中块尺寸的合理选择问题,得出以下结论:
1)块尺寸对估值精度的影响。在可接受的块尺寸范围内,待估块尺寸越小估计方差越大;在开采工作面尺寸固定的情况下,生产单元越小离差方差越大。为保证估值精度,在资源储量估算中应适当选择较大的块尺寸。
2)块尺寸对品位-吨位的影响。在一定范围内改变块体尺寸,资源储量估算总体结果相近;当块尺寸超出某一临界值,储量估算结果将出现剧烈波动。为保证储量估算的边界拟合精度,不应该选择过大的块尺寸。
3)块尺寸的合理选择。在资源不同开发阶段,应用地质统计学进行资源储量估算,块尺寸的选择依据不同。在地质勘探阶段,存在理论最优块尺寸值,但是该数值一般较大,块尺寸主要受边界拟合精度限制。建议在边界拟合精度允许的条件下,适当选择较大的块尺寸。在矿山生产阶段,块尺寸应该与选别开采单元一致。该尺寸的确定需要从地质因素、技术因素和经济因素3个方面进行综合考虑。
| [1] | 侯景儒, 黄竞先. 地质统计学在固体矿产资源/储量分类中的应用[J]. 地质与勘探, 2001, 37 (6) : 61-66. Hou Jingru, Huang Jingxian. Application of Geostatistics in Classification for Resources/Reserves of Solid Fuels and Mineral Commodities[J]. Geology and Exploration, 2001, 37 (6) : 61-66. |
| [2] | 张剑波, 李谢清, 石阳, 等. 油藏数值模拟中地质模型的建模流程与方法[J]. 吉林大学学报(地球科学版), 2015, 45 (3) : 860-868. Zhang Jianbo, Li Xieqing, Shi Yang, et al. Processes and Technology of Three-Dimensional Geological Modeling System in Numerical Reservoir Simulation[J]. Journal of Jilin University (Earth Science Edition), 2015, 45 (3) : 860-868. |
| [3] | 初道忠, 王青, 任凤玉, 等. 谦比西铜矿石品位分布的地质统计学研究[J]. 金属矿山, 2006, 363 (9) : 57-59. Chu Daozhong, Wang Qing, Ren Fengyu, et al. Study on Grade Distribution of Chambishi Copper Ore Using Geological Statistics[J]. Metal Mine, 2006, 363 (9) : 57-59. |
| [4] | 郭怀成, 周丰, 刀谞. 地统计方法学研究进展[J]. 地理研究, 2008, 27 (5) : 1191-1202. Guo Huaicheng, Zhou Feng, Dao Xu. State-of-Art on Geostatistical Methodology[J]. Geographical Research, 2008, 27 (5) : 1191-1202. |
| [5] | 高航校, 任小华, 郭健. 资源量分类中勘查工程间距的确定方法研究[J]. 地质与勘探, 2014, 50 (2) : 340-345. Gao Hangxiao, Ren Xiaohua, Guo Jian. A Method of Determining Grid Spacing in Surveys for Classification of Mineral Reserves[J]. Geology and Exploration, 2014, 50 (2) : 340-345. |
| [6] | 杨利容.复杂矿体结构三维建模与储量计算方法研究:以某地区铀矿床为例[D].成都:成都理工大学, 2013. Yang Lirong.Research on 3D Modeling of Complex Orebody Structure and Reserve Calculation with Uranium Deposits as an Example[D].Chengdu:Chengdu University of Technology, 2013. |
| [7] | 宋宇, 崔志勇. 袁家村铁矿矿床地质模型[J]. 矿业工程, 2014, 12 (3) : 60-62. Song Yu, Cui Zhiyong. Geological Model for Yuanjiacun Iron Ore Deposit[J]. Mining Engineering, 2014, 12 (3) : 60-62. |
| [8] | 倪平泽, 刘修国, 李超岭, 等. 3D矿床建模技术在数字矿产勘查中的应用[J]. 地球科学:中国地质大学学报, 2010, 35 (3) : 444-452. Ni Pingze, Liu Xiuguo, Li Chaoling, et al. 3D Ore Deposit Modeling and Application in Digital Mineral Survey[J]. Earth Science:Journal of China University of Geosciences, 2010, 35 (3) : 444-452. DOI:10.3799/dqkx.2010.054 |
| [9] | 李晓晖, 袁峰, 张明明, 等. 基于Surpac的垂直断面资源储量估算方法研究与实现[J]. 吉林大学学报(地球科学版), 2015, 45 (1) : 156-165. Li Xiaohui, Yuan Feng, Zhang Mingming, et al. Research and Implementation of Section Method in Reserve Estimation Based on Surpac[J]. Journal of Jilin University (Earth Science Edition), 2015, 45 (1) : 156-165. |
| [10] | 任娜.基于八叉树的复杂矿体块体模型构建方法研究[D].武汉:中国地质大学, 2012. Ren Na.Research on Construction Method of Block Model for Complicated Ore Body Based on the Octree[D].Wuhan:China University of Geosciences, 2012. |
| [11] | 孙玉建. 资源储量估算中确定合理的矿体离散尺寸[J]. 中国矿业, 2011, 20 (7) : 14-15. Sun Yujian. To Define Reasonable Dispersing Size for Orebody in Estimation of Mineral Resources and Reserves[J]. China Mining, 2011, 20 (7) : 14-15. |
| [12] | 赵战锋, 周坤, 王玲. 三维地质建模中设定矿块尺寸探讨[J]. 有色金属(矿山部分), 2012, 64 (4) : 83-86. Zhao Zhanfeng, Zhou Kun, Wang Ling. Discussion on Block Size Setting in 3D Geological Modeling[J]. Non-Ferrous Metals, 2012, 64 (4) : 83-86. |
| [13] | 程志刚. 试论最低工业品位和矿块大小[J]. 有色金属(矿山部分), 1991, 6 (3) : 32-34. Cheng Zhigang. Study on the Lowest Industrial Grade and Block Size[J]. Non-Ferrous Metals, 1991, 6 (3) : 32-34. |
| [14] | 司永年. 金属露天矿分采单元规格问题[J]. 金属矿山, 1983, 7 (7) : 20-25. Si Yongnian. Research for Unit Specification Problem on Metallic Open Pit Mining[J]. Metal Mine, 1983, 7 (7) : 20-25. |
| [15] | 陈希廉. 矿体三维模型与计算机地质制图发展方向探讨[J]. 有色金属矿产与勘查, 2000, 9 (1) : 19-23. Chen Xilian. Study on the Development Direction of Ore Body Three-Dimensional Geological Modeling and the Computer Graphics[J]. Geology Exploration for Non-Ferrous Metals, 2000, 9 (1) : 19-23. |
| [16] | 贾明涛, 潘长良, 王李管. 克服地质统计学矿床建模中主观因素影响技术研究[J]. 地质与勘探, 2003, 39 (4) : 73-77. Jia Mingtao, Pan Changliang, Wang Liguan. The Technology to Overcome Effects of Subjective Factors in Deposit Modeling Using Geostatistics[J]. Geology and Exploration, 2003, 39 (4) : 73-77. |
| [17] | 袁怀雨, 刘保顺, 李克庆. 合理入选品位整体动态优化[J]. 北京科技大学学报, 2002, 24 (3) : 239-242. Yuan Huaiyu, Liu Baoshun, Li Keqing. United Dynamic Optimization Study on the Rational Beneficiation Feed Grade[J]. Journal of University of Science and Technology Beijing, 2002, 24 (3) : 239-242. |
| [18] | 李克庆, 秦元萍, 刘保顺, 等. 铁精矿品位优化通用系统[J]. 北京科技大学学报, 2005, 27 (1) : 114-118. Li Keqing, Qin Yuanping, Liu Baoshun, et al. General Optimization System of Iron Concentrate Grade[J]. Journal of University of Science and Technology Beijing, 2005, 27 (1) : 114-118. |


