2. 中国地质大学(北京)海相储层演化与油气富集机理教育部重点实验室, 北京 100083;
3. 中国地质大学(北京)页岩气勘查与评价国土资源部重点实验室, 北京 100083;
4. 中国石油大学地球科学与技术学院, 山东 青岛 266555;
5. 中国石油新疆油田分公司风城油田作业区, 新疆 克拉玛依 834000
2. Key Laboratory for Marine Reservoir Evolution and Hydrocarbon Abundance Mechanism, Ministry of Education, China University of Geosciences, Beijing 100083, China;
3. Key Laboratory for Shale Gas Exploitation and Assessment, Ministry of Land and Resources, China University of Geosciences, Beijing 100083, China;
4. School of Geosciences, China University of Petroleum, Qingdao 266555, Shandong, China;
5. Fengcheng Oil Field Operation Area, Xinjiang Oil Field Branch Company, PetroChina, Karamay 834000, Xinjiang, China
0 引言
长期油气勘探和实践证实,采用构造应力场数值模拟方法进行储层构造裂缝预测具有良好的理论基础,是一种比较可靠的构造裂缝定量预测方法[1-5]。大量研究表明,构造裂缝的形成与分布受地应力场、构造部位、岩石组构、岩层厚度、沉积微相、孔隙流体等诸多地质因素共同控制[6-8]。构造应力场模拟与区域地质基础工作紧密结合,从影响储层构造裂缝形成与发育的地质因素入手,形成和发展了一套以有限元数值模拟为基础,进行裂缝定量预测的研究方法[9-11]。该方法既严格考虑了裂缝的成因机制,又能与油气生产中静态-动态资料相结合,因此,在油田中取得了较好的应用效果。
裂缝产状在量化裂缝性油藏各向异性中起决定性作用[12],裂缝产状的演化特征对确定不同地质时期油气运聚、成藏同样具有指示意义,也是准确预测现今裂缝开启压力、有效开度及渗透率等参数的前提。裂缝倾向的作用是将储层裂缝参数各向异性在水平面内不同方位上进行劈分;裂缝倾角的作用是将储层裂缝参数各向异性在铅直剖面内不同方位上进行劈分。但在实践中,运用应力场数值模拟方法对构造裂缝产状预测时,并未考虑后期构造运动对裂缝产状的改造作用,致使在后期量化裂缝参数各向异性时出现较大的误差,难以符合油田合理高效开发的要求。
1 岩石破裂准则的优选储层岩石在受到应力作用产生破裂时,遵循一定的数学准则。岩石受力发生破坏作用产生裂缝可用以下通式表示:
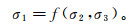 (1)
(1) 公式(1)称为破裂准则;σ1为最大主应力,MPa;σ2为中间主应力,MPa;σ3为最小主应力,MPa。库伦-莫尔(Mohr-Coulomb)准则和格里菲斯(Griffith)准则是脆性砂岩最常用的破裂准则[13-15]。
若岩石受力破坏形成的裂缝是剪切性质或以剪切性质为主,适用库伦-莫尔准则:
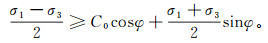 (2)
(2) 式(2)中:C0为岩石内聚力,MPa;φ为岩石内摩擦角,(°)。
若形成的是张性或以张性为主的裂缝,适用格里菲斯准则,在三维应力条件下:
当(σ1+3σ3)>0时,破裂准则为
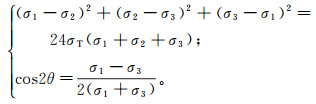 (3)
(3) 当(σ1+3σ3)≤0时,破裂准则可简化为
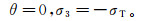 (4)
(4) 公式(3)-(4)中:σT为岩石单向拉伸试验中岩石的抗拉强度,MPa;θ为岩石破裂角,(°)。
2 裂缝形成时产状预测在应力场数值模拟中,设裂缝形成时所在平面的单位法向矢量为n′,倾角为η′,倾向为γ′。依据岩石破裂准则,可以得到应力场坐标系(σ1、σ2、σ3方向分别代表 3个坐标轴方向)中裂缝的产状[13, 16],主应力方向与大地坐标系X-Y-Z轴的夹角分别如下:
①σ1与X-Y-Z轴的夹角:α11、α12、α13;
②σ2与X-Y-Z轴的夹角:α21、α22、α23;
③σ3与X-Y-Z轴的夹角:α31、α32、α33。
以岩石剪切破裂为例,在应力场坐标系中产生的两组裂缝面的单位法向矢量可表示为
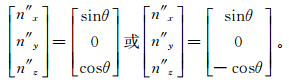 (5)
(5) 矢量n′在大地坐标系中可以表示为
 (6)
(6) 依据公式(6),计算裂缝形成时的倾角η′、倾向γ′:
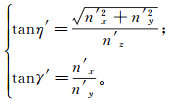 (7)
(7) 得到裂缝形成时的倾角η′:
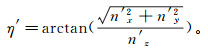 (8)
(8) 裂缝形成时的倾向γ′需分象限进行讨论:
①n′x≥0且n′y >0,裂缝形成时的倾向为北东向,此时:
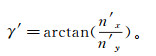 (9)
(9) ②n′x≤0且n′y>0,裂缝形成时的倾向为东南向,此时:
 (10)
(10) ③n′x < 0且n′y≤0,裂缝形成时的倾向为西南向,此时:
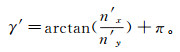 (11)
(11) ④n′x≥0且n′y < 0,裂缝形成时的倾向为北西向,此时:
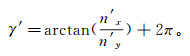 (12)
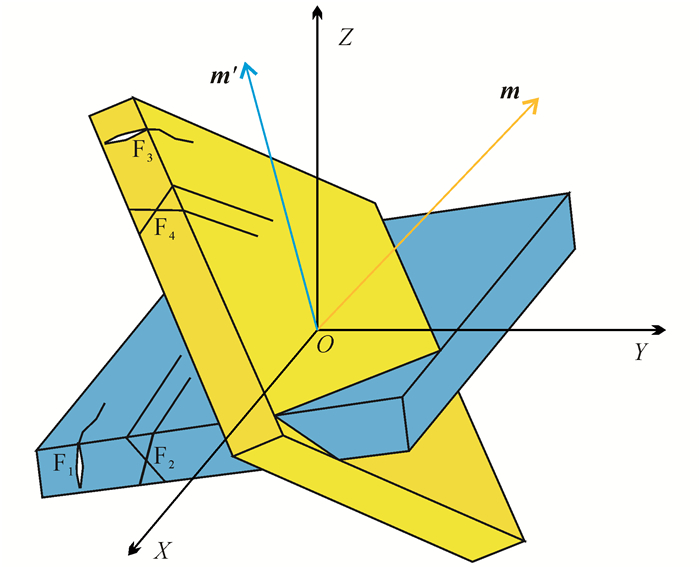
(12) 地下岩层受应力作用破裂产生裂缝后,后期构造运动对裂缝的改造作用可以借助于适当的理论模型进行研究。裂缝形成发育主要受岩石力学层的控制[17-19]。在恢复不同时期古构造形态的基础上,得到对应岩层的产状,借助于早期-晚期岩石力学层建立裂缝空间转换模型(图 1),定量分析裂缝产状的变化。为了满足研究需要,将理论模型作适当简化,假设:
①裂缝主要在单一岩石力学层内发育,在平面、剖面上没有切穿不同的岩石力学层。
②在后期构造运动中,裂缝与岩石力学层间不发生相对位移、旋转。
|
| F1.早期张裂缝;F2.早期剪裂缝;F3.晚期张裂缝;F4.晚期剪裂缝。 图 1 裂缝空间转换理论模型 Figure 1 The space conversion model of frecture |
|
|
如图 1所示,设早期岩层所在平面的单位法向矢量为m′,倾角为δ′,倾向为ω′;晚期岩层所在平面的单位法向矢量为m,倾角为δ,倾向为ω;在早期岩层中,裂缝所在平面的单位法向矢量为n′,倾角为η′,倾向为γ′;在晚期岩层中,裂缝所在平面的单位法向矢量为n,倾角为η,倾向为γ。
矢量m在大地坐标系中的3个分量为
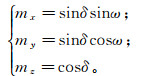 (13)
(13) 矢量m′在大地坐标系中的3个分量为
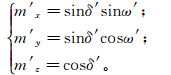 (14)
(14) 利用建立的裂缝空间转换理论模型,矢量m、m′所在平面的法向矢量p′在大地坐标系中的3个分量表示为
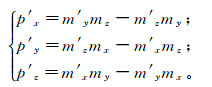 (15)
(15) 公式(15)中,p′z < 0时,矢量p′在大地坐标系中的3个分量可表示为
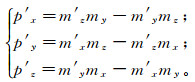 (16)
(16) 矢量p′的单位法向矢量p在大地坐标系中的3个分量可表示为
 (17)
(17) 旋转矢量p与坐标轴重合,后绕该坐标轴旋转,使早期岩层与晚期岩层重合,最后将矢量p逆向旋回,实现早期岩层与晚期岩层耦合。
如图 2所示,将矢量p绕X轴旋转,使其位于XOZ面上,当py≥0时,旋转角ξ1为正值;反之,旋转角ξ1为负值,旋转矩阵T1可表示为
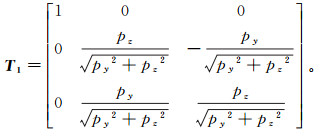 (18)
(18)
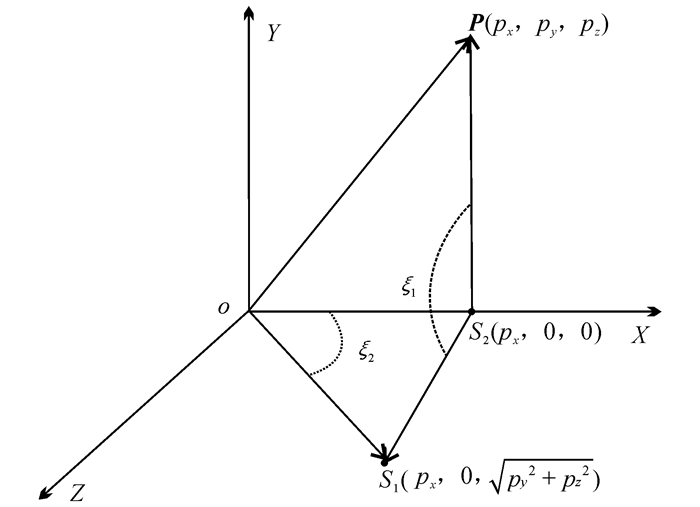
|
| 图 2 旋转角ξ1、ξ2确定示意图 Figure 2 Schematic diagram of rotation angleξ1 and ξ2 |
|
|
将矢量p绕Y轴旋转,使矢量p的方向与X轴方向重合,旋转矩阵T2表示为
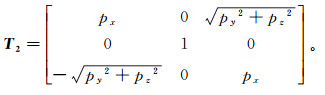 (19)
(19) 矢量m、m′经过两次坐标旋转,对应的矢量表示为h、h′。矢量h在大地坐标系中可以表示为
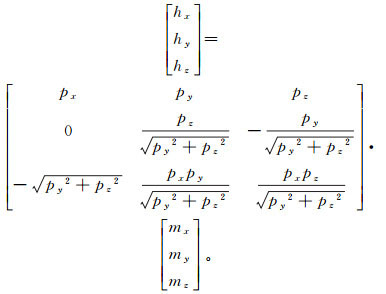 (20)
(20) 矢量h′在大地坐标系中的3个分量表示为
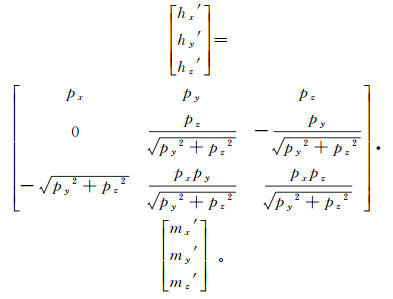 (21)
(21) 如图 3所示,矢量h、h′与Y轴正方向的方位角ξ3、ξ4分别表示为
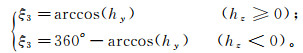 (22)
(22) 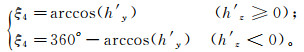 (23)
(23)

|
| 图 3 旋转角ξ3、ξ4确定示意图 Figure 3 Schematic diagram of the rotation angle ξ3 and ξ4 |
|
|
矢量h′旋转ξ与矢量h重合,则旋转角ξ可表示为
 (24)
(24) 公式(24)可确定早期-晚期岩层耦合的旋转角ξ的大小、方向,矢量h′与h重合的旋转矩阵T3表示为
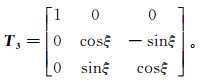 (25)
(25) 将矢量p逆向旋回原位置,首先绕Y轴旋-ξ2,旋转矩阵T4表示为
 (26)
(26) 之后,将矢量p绕X轴旋转-ξ1,旋转矩阵T5表示为
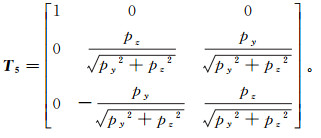 (27)
(27) 综合公式(18)(27),使早期岩层与晚期岩层重合的旋转矩阵T可表示为
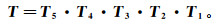 (28)
(28) 整理后,矩阵T表示为
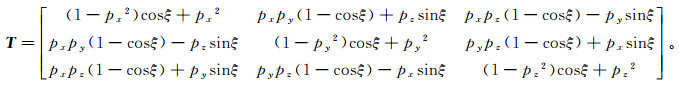 (29)
(29) 结合裂缝所在岩层的运动学特征以及早期裂缝的产状,求得改造后裂缝的产状。早期裂缝面的单位法向矢量n′在3个坐标轴的投影表示为
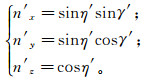 (30)
(30) 结合公式(29),构造运动改造后晚期裂缝面的单位法向矢量n在大地坐标系中的投影可以表示为
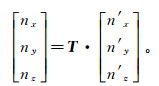 (31)
(31) 依据公式(7)-(12)可计算裂缝不同时期的产状。
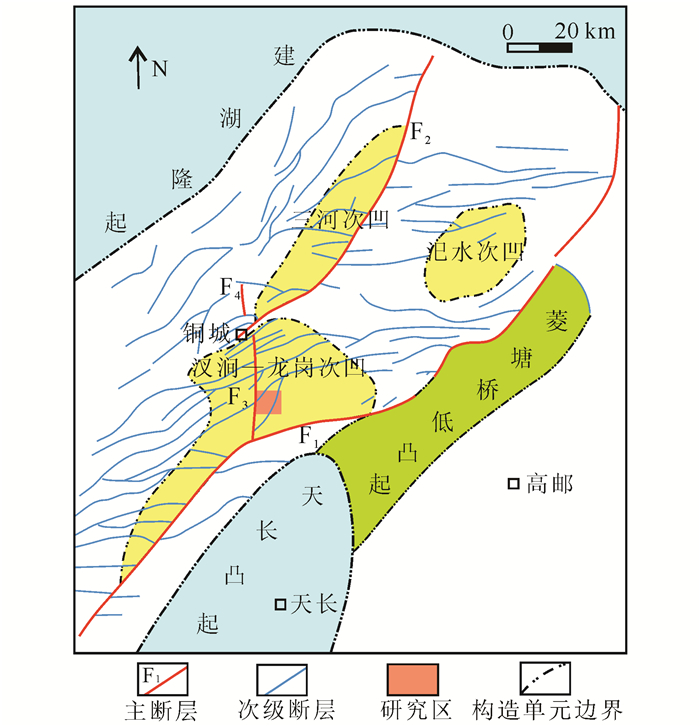
4 实例应用 4.1 区域地质概况铜城断裂带构造上位于苏北盆地金湖凹陷的中部,是划分汊涧-龙岗次凹的盆地内区带级右旋走滑断层,南部交汇于金湖凹陷的边界杨村断层,向北消失于铜城地区(图 4)。平面上,该断层表现为一条线状主位移带,主干断层两侧雁列断层发育;空间中,主断层倾向东西摇摆,出现“丝带效应”[20]。铜城地区主力油气层为阜二段,岩性以低渗透粉砂岩为主,裂缝在油气渗流中起至关重要的作用。
阜二段沉积以来,主要经历了吴堡和三垛两期构造运动,区域应力场演化及构造型式的演化规律如下:
1)阜宁运动晚期,受近南北向拉张应力作用,断层活动数量骤增,铜城断层次级断层逐次形成;吴堡事件在阜二段裂缝的形成中起到至关重要的作用,后期的构造事件对裂缝主要起改造作用[21-22]。
2)戴南期,吴堡运动使阜宁组遭受剥蚀,地层厚度相对较薄,断层活动性逐渐减弱,基本没有新生断层,先前形成的断层继续活动[23-26]。
3)三垛组沉积期,受近东西向挤压力作用,地层逆冲,形成轴向沿铜城断层走向的断展背斜;三垛组沉积末期,受郯庐断裂活动的影响,苏北盆地内主控断层产生右行扭动,铜城断层表现出典型的“P”剪切走滑断层性质,两盘的次级断层被铜城断层错开[23-26]。
4)新近纪和第四纪铜城地区表现为整体下陷,只有少量断层继承性活动,但断层落差很小,基本维持了先期的构造格局[26]。
4.2 裂缝产状演化特征单井岩心描述结果判断,阜二段裂缝力学性质以剪裂缝为主(87%),靠近断层的井位裂缝发育,断层与裂缝为同一应力场作用下的产物[21-22]。通过取心岩样力学实验确定阜二段岩石单轴抗拉强度为2.4 MPa,单轴抗剪强度为6.5 MPa,其他岩石力学参数如表 1。
| 泊松比 | 弹性模量/GPa | 密度/(g/cm3) | |
| 砂岩层 | 0.15 | 5.6 | 2.21 |
| 断裂带 | 0.20 | 5.0 | 2.20 |
| 泥岩层 | 0.23 | 4.5 | 2.10 |
| 围岩 | 0.15 | 5.5 | 2.22 |
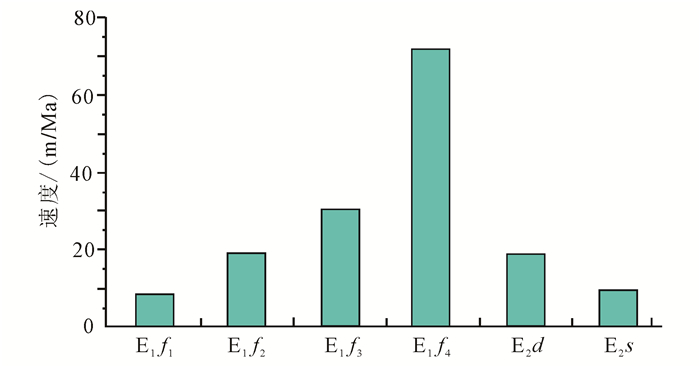
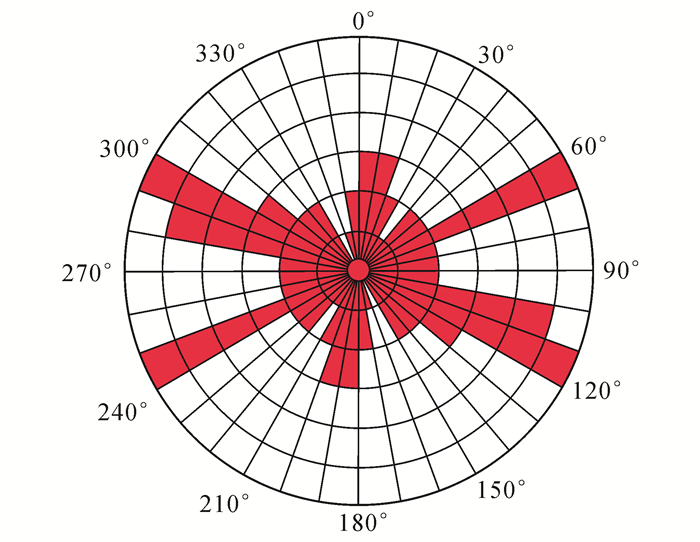
构造活动强弱对裂缝形成起控制作用。铜城地区构造活动高强点为阜宁晚期(图 5),结合该时期活动断裂走向、性质、组合规律及岩心裂缝走向(图 6)[27],确定铜城断裂带吴堡运动期水平拉张应力方向为近南北向,这也与临近闵桥、桥河口、石港地区阜二段储层[21-22]裂缝的形成时期、古应力场相吻合,同为近地表条件下形成[27-28];以单井岩心裂缝线密度为约束条件,采用等效古应力法[9-10]反演裂缝形成时期的古应力场,结合地应力与构造裂缝参数之间的定量关系[3, 9-11],通过不断地反演、拟合,最终确定在地质模型的南北边界施加8 MPa的拉张应力,东西边界施加2.5 MPa的拉张应力,垂向应力由ANSYS软件自动生成。
|
| 图 5 铜城断裂带不同时期断层活动速率对比图 Figure 5 Fault activity rate of different periods in the Tongcheng fault zone |
|
|
|
| 图 6 研究区岩心裂缝走向玫瑰花图 Figure 6 Rose diagram of core fracture strike of study area |
|
|
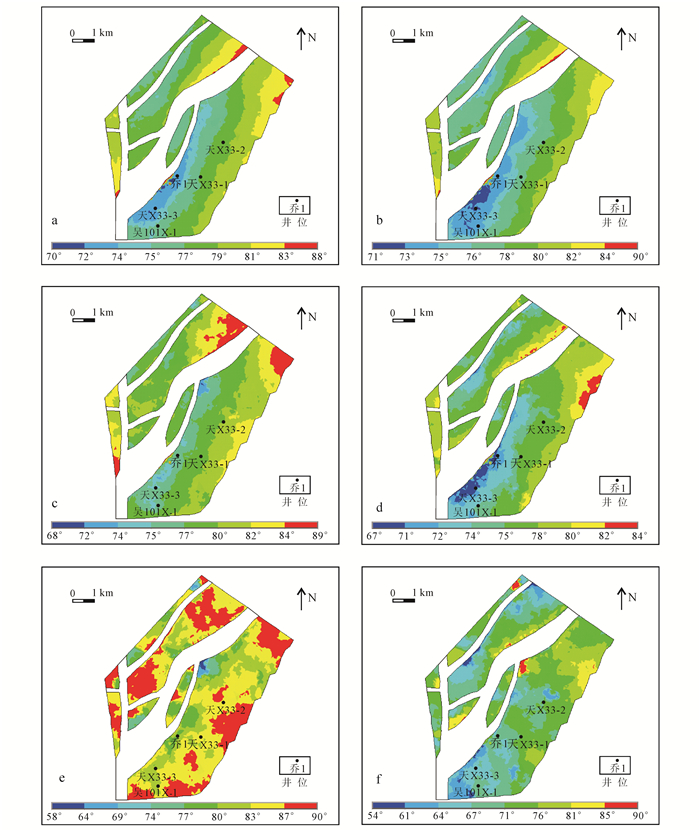
在恢复不同时期古构造形态的基础上[29-30],借助于阜二段岩层的三维空间展布,建立不同地质历史时期的裂缝空间转换理论模型,采用公式(13)(31)分析裂缝形成后的运动学特征,依据公式(7)(12)得到裂缝产状分布(图 7),约定裂缝形成时期南倾裂缝为Ⅰ组裂缝,北倾裂缝为Ⅱ组裂缝。
|
| a.戴南沉积前Ⅰ组;b.戴南沉积前Ⅱ组;c.三垛沉积前Ⅰ组;d.三垛沉积前Ⅱ组;e.现今Ⅰ组;f.现今Ⅱ组。 图 7 研究区裂缝倾角分布图 Figure 7 Distribution of fracture dip of presen |
|
|
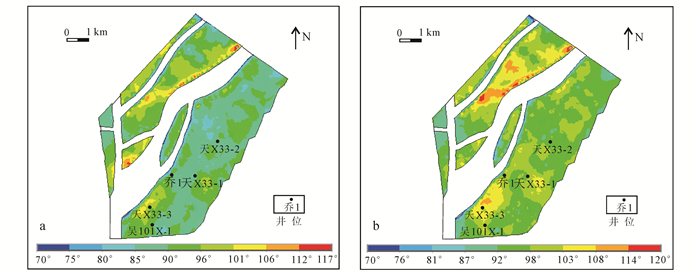
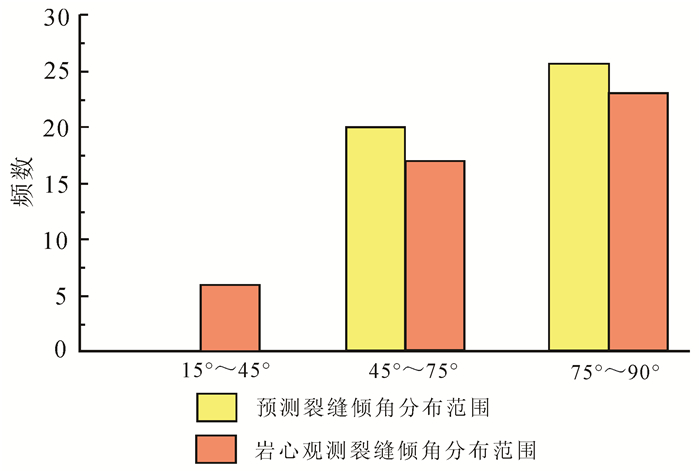
为了验证所模拟的裂缝产状演化规律的准确性,将单井岩心裂缝产状与现今构造裂缝数值模拟结果进行了对比。采用传统应力场数值模拟[13, 15]得到裂缝的倾角集中在85°,走向集中在86°~94°;通过多期构造运动对裂缝演化规律分析,得到的倾角分布范围为55°~90°,走向分布范围为70°~125°,该结果与岩心观测结果基本一致(图 6,图 8,图 9),认为本文所提的表征裂缝产状演化规律的方法同样能够提高裂缝产状预测的精度。
|
| 图 8 研究区现今Ⅰ组(a)和Ⅱ组(b)裂缝走向分布图 Figure 8 Distribution of Ⅰ group (a) Ⅱ group (b) of fracture strike of present |
|
|
|
| 图 9 岩心观测-数值模拟预测裂缝倾角对比图 Figure 9 The fracture dip comparison figure of the core observation and numerical simulation prediction |
|
|
结合铜城地区构造演化、应力场演化,将该区裂缝产状演化(图 7,图 8)分为3个阶段:
1)裂缝形成发育阶段。阜宁运动晚期,受近南北向拉张应力作用,新断层以及活动断层的数量骤增,阜二段储层裂缝普遍发育;产生南倾、北倾的两组裂缝;总体上,在构造高部位裂缝倾角为低值,构造低部位为高值;在靠近断层的乔1井附近有少量张裂缝产生。
2)裂缝继承发展阶段。戴南运动期,少有新断层产生,多为断层继承性活动,活动断层落差小,阜二段地层基本保持平缓的构造格局;与岩层倾向一致的裂缝倾角进一步增大;与岩层倾向相反的裂缝倾角逐渐减小。
3)裂缝差异分离阶段。三垛沉积期,区域应力场发生改变,由拉张转变为东西方向的挤压;少部分正断层发生构造反转变为逆冲断层,在断层的上盘阜二段发生明显弯曲,发育断层相关褶皱[26];盐城运动期构造缓和,基本无新生断层形成,对阜宁组的构造没有明显的改造作用,仅仅使其埋深加大。三垛沉积期的阜二段逆冲作用,上覆岩层的差异沉降形成了现今两组裂缝分别以垂直缝、高角度斜交缝为主的格局;在构造低部位裂缝倾角大,甚至出现倾向反转的现象。
5 结论1)通过确定研究区裂缝力学性质、岩石力学参数,在恢复古构造形态的基础上,对裂缝形成时期古应力场数值模拟后选择适用性的岩石破裂准则,借助于早期岩层、晚期岩层的三维空间变化规律,建立了不同构造活动时期的裂缝空间转换理论模型,并推导相应的数学算法,该思路是定量分析裂缝演化规律的有效手段。
2)结合铜城断裂带断层演化以及裂缝产状变化,认为阜二段储层构造裂缝经历了阜宁运动晚期裂缝形成发育、戴南运动期裂缝继承发展、三垛运动期裂缝差异分离3个阶段;现今发育的两组构造裂缝分别以垂直缝、高角度斜交缝为主。
3)将单井岩心裂缝产状与现今构造裂缝数值模拟结果进行了对比,岩层的差异运动使该区两组裂缝发生了不同的演化结果,预测得到裂缝的倾角、走向分布范围与岩心观测结果基本一致。本文所提模拟裂缝产状演化规律的思路,同样能够提高现今裂缝产状预测的精度。
| [1] | 周新桂, 张林炎, 屈雪峰, 等. 沿河湾探区低渗透储层构造裂缝特征及分布规律定量预测[J]. 石油学报, 2009, 30 (2) : 195-200. Zhou Xingui, Zhang Linyan, Qu Xuefeng, et al. Characteristics and Quantitative Prediction of Distribution Laws of Tectonic Fractures of Low-Permeability Reservoirs in Yanhewan Area[J]. Acta Petrolei Sinica, 2009, 30 (2) : 195-200. |
| [2] | Titeux M, Janson X, Srinivasan S, et al.Facies Dis-tribution in Collapsed Carbonate Karsts:A Mechanical Approach[C]//AAPG.Houston:AAPG Annual Convention & Exhibition, 2011:1-4. |
| [3] | 季宗镇, 戴俊生, 汪必峰. 地应力与构造裂缝参数间的定量关系[J]. 石油学报, 2010, 33 (1) : 68-72. Ji Zongzhen, Dai Junsheng, Wang Bifeng. Quantitative Relationship Between Crustal Stress and Parameters of Tectonic Facture[J]. Acta Petrolei Sinica, 2010, 33 (1) : 68-72. |
| [4] | 陈树民, 姜传金, 刘立, 等. 松辽盆地徐家围子断陷火山岩裂缝形成机理[J]. 吉林大学学报(地球科学版), 2014, 44 (6) : 1816-1826. Chen Shumin, Jiang Chuanjin, Liu Li, et al. Fracture Formation Mechanism of Volcanic Rocks in Xujiaweizi Fault Depression of Songliao Basin[J]. Journal of Jilin University (Earth Scicncc Edition), 2014, 44 (6) : 1816-1826. |
| [5] | 李小刚, 徐国强, 韩剑发, 等. 断层裂缝定量描述技术在塔中X井区良里塔格组裂缝研究中的应用[J]. 吉林大学学报(地球科学版), 2012, 42 (2) : 344-352. Li Xiaogang, Xu Guoqiang, Han Jianfa, et al. Application of a New Method for Quantitative Calculating of Fault-Related Fracture:A Case Study from Lianglitage Formation in Tazhong X Well Area, Tarim Basin, China[J]. Journal of Jilin University (Earth Scicncc Edition), 2012, 42 (2) : 344-352. |
| [6] | 赵永刚, 陈景山, 李凌, 等. 基于残余岩溶强度表征和裂缝预测的碳酸盐岩储层评价:以塔中西部上奥陶统良里塔格组为例[J]. 吉林大学学报(地球科学版), 2015, 45 (1) : 25-36. Zhao Yonggang, Chen Jingshan, Li Ling, et al. Evaluation of Carbonate Reservoir Based on Residual Karst Intensity Characterization and Structural Fracture Prediction:A Case from the Upper Ordovician Lianglitage Formation in the West of Center Tarim Basin[J]. Journal of Jilin University:(Earth Scicncc Edition), 2015, 45 (1) : 25-36. |
| [7] | 曾联波. 低渗透砂岩储层裂缝的形成与分布[M]. 北京: 科学出版社, 2008 : 18-27, 101-125. Zeng Lianbo. Formation and Distribution of Fractures in Low-Permeability Sandstone Reservoirs[M]. Beijing: Science Press, 2008: 18-27, 101-125. |
| [8] | 侯贵廷, 潘文庆. 裂缝地质建模及力学机制[M]. 北京: 科学出版社, 2013 : 62-147, 180-181. Hou Guiting, Pan Wenqing. Fracture Geological Modeling and Its Mechanism[M]. Beijing: Science Press, 2013: 62-147, 180-181. |
| [9] | 戴俊生, 冯建伟, 李明, 等. 砂泥岩间互地层裂缝延伸规律探讨[J]. 地学前缘, 2011, 18 (2) : 277-283. Dai Junsheng, Feng Jianwei, Li Ming, et al. Discussion on the Extension Law of Structural Fracture in Sand-Mud Interbed Formation[J]. Earth Science Frontiers, 2011, 18 (2) : 277-283. |
| [10] | 季宗镇, 戴俊生, 汪必峰, 等. 构造裂缝多参数定量计算模型[J]. 中国石油大学学报(自然科学版), 2010, 34 (1) : 24-28. Ji Zongzhen, Dai Junsheng, Wang Bifeng, et al. Multi-Parameter Puantitative Calculation Model for Tectonic Fracture[J]. Journal of China University of Petroleum (Natural Science Edition), 2010, 34 (1) : 24-28. |
| [11] | 冯建伟, 戴俊生, 马占荣, 等. 低渗透砂岩裂缝参数与应力场关系理论模型[J]. 石油学报, 2011, 32 (4) : 664-671. Feng Jianwei, Dai Junsheng, Ma Zhanrong, et al. The Theoretical Model Between Fracture Parameters and Stress Field of Low-Permeability Sandstones[J]. Acta Petrolei Sinica, 2011, 32 (4) : 664-671. |
| [12] | 刘月田, 丁祖鹏, 屈亚光, 等. 油藏裂缝方向表征及渗透率各向异性参数计算[J]. 石油学报, 2011, 32 (5) : 842-846. Liu Yuetian, Ding Zupeng, Qu Yaguang, et al. The Characterization of Fracture Orientation and the Calculation of Anisotropic Permeability Parameters of Reservoirs[J]. Acta Petrolei Sinica, 2011, 32 (5) : 842-846. |
| [13] | 文世鹏, 李德同. 储层构造裂缝数值模拟技术[J]. 石油大学学报(自然科学版), 1996, 20 (5) : 17-24. Wen Shipeng, Li Detong. Numerical Simulation Technology for Structural Fracture of Reservoir[J]. Journal of China University of Petroleum (Natural Science Edition), 1996, 20 (5) : 17-24. |
| [14] | 戴俊生, 汪必峰, 马占荣. 脆性低渗透砂岩破裂准则研究[J]. 新疆石油地质, 2007, 28 (4) : 393-395. Dai Junsheng, Wang Bifeng, Ma Zhanrong. Research on Cracking Principles of Brittle Low-Permeability Sands[J]. Xinjiang Petroleum Geology, 2007, 28 (4) : 393-395. |
| [15] | 周新桂, 张林炎, 范昆. 含油气盆地低渗透储层构造裂缝定量预测方法和实例[J]. 天然气地球科学, 2007, 18 (3) : 328-333. Zhou Xingui, Zhang Linyan, Fan Kun. Methods for Quantitative Prediction of Tectonic Fractures in Compact Reservoirs in Petroliferous Basins and a Case Study[J]. Natural Gas Geoscience, 2007, 18 (3) : 328-333. |
| [16] | 冯陈东, 戴俊生, 王霞田, 等. 不同坐标系中裂缝渗透率的定量计算[J]. 石油学报, 2011, 32 (1) : 135-139. Feng Chendong, Dai Junsheng, Wang Xiatian, et al. Quantitative Calculation of the Tectonic Fracture Permeability in Different Coordinate Systems[J]. Acta Petrolei Sinica, 2011, 32 (1) : 135-139. |
| [17] | Bai T, Pollard, David D. Closely Space Fractures in Layered Rocks:Initiation Mechanism and Propagation Kinematics[J]. Journal of Structural Geology, 2000, 22 (10) : 1409-1425. DOI:10.1016/S0191-8141(00)00062-6 |
| [18] | 刘之的, 汤小燕, 于红果, 等. 基于岩石力学参数评价火山岩裂缝发育程度[J]. 天然气工业, 2009, 29 (11) : 20-24. Liu Zhidi, Tang Xiaoyan, Yu Hongguo, et al. Evaluation of Fracture Development in Volcanic Rocks Based on Rock Mechanical Parameters[J]. Natural Gas Industry, 2009, 29 (11) : 20-24. |
| [19] | Chad A, Underwood M L, Cooke J A, et al. Stra-tigraphic Controls on Vertical Fracture Patterns in Silarian Dolomite, Northeastern Wisconsin[J]. AAPG Bulletin, 2003, 87 (1) : 121-142. |
| [20] | 叶绍东. 金湖凹陷铜城断层构造特征与油气成藏[J]. 地质力学学报, 2012, 18 (2) : 187-194. Ye Shaodong. Structural Characteristics of Tongcheng Fault and Hydrocarbon Accumulation in Jinhu Sag[J]. Journal of Geomechanics, 2012, 18 (2) : 187-194. |
| [21] | 刘敬寿, 戴俊生, 邹娟, 等. 裂缝性储层渗透率张量定量预测方法[J]. 石油与天然气地质, 2015, 36 (6) : 1022-1029. Liu Jingshou, Dai Junsheng, Zou Juan, et al. Quantitative Prediction of Permeability Tensor of Fractured Reservoirs[J]. Oil & Gas Geology, 2015, 36 (6) : 1022-1029. |
| [22] | 刘肖军. 苏北盆地桥河口油田阜二段第三砂层组裂缝参数模拟计算[J]. 石油与天然气地质, 2010, 31 (2) : 250-254. Liu Xiaojun. Simulation of Fracture Parameters in the 3rd Sand Unit of the Paleogene Fu-2 Member in the Qiaohekou Oilfield[J]. Oil & Gas Geology, 2010, 31 (2) : 250-254. |
| [23] | 能源, 漆家福, 张春峰, 等. 金湖凹陷石港断层构造演化及油气聚集特征[J]. 石油学报, 2009, 30 (5) : 667-671. Neng Yuan, Qi Jiafu, Zhang Chunfeng, et al. Structural Evolution of Shigang Fault and Features of Hydrocarbon Accumulation in Jinhu Sag[J]. Acta Petrolei Sinica, 2009, 30 (5) : 667-671. |
| [24] | 能源, 漆家福, 张春峰, 等. 金湖凹陷断裂特征及其石油地质意义[J]. 大地构造与成矿学, 2012, 36 (1) : 16-23. Neng Yuan, Qi Jiafu, Zhang Chunfeng, et al. Structural Features of the Jinhu Sag in the Subei Basin and Its Petroleum Geological Significance[J]. Geotectonica et Metallogenia, 2012, 36 (1) : 16-23. |
| [25] | 王伟锋, 周维维, 周杰, 等. 金湖凹陷隐性断裂带形成机制及分布[J]. 吉林大学学报(地球科学版), 2014, 44 (5) : 1395-1405. Wang Weifeng, Zhou Weiwei, Zhou Jie, et al. Formation Mechanism and Distribution of Buried Fault Zones in the Jinhu Sag[J]. Journal of Jilin University (Earth Scicncc Edition), 2014, 44 (5) : 1395-1405. |
| [26] | 张祥成, 戴俊生, 邹娟, 等. 金湖凹陷铜城断裂带断层活动特征[J]. 地质力学学报, 2014, 20 (4) : 424-433. Zhang Xiangcheng, Dai Junsheng, Zou Juan, et al. Fault Activity Features of Tongcheng Fault Zone in Jinhu Sag[J]. Journal of Geomechanics, 2014, 20 (4) : 424-433. |
| [27] | 刘敬寿, 戴俊生, 王珂, 等. 斜井岩心裂缝产状校正方法及其应用[J]. 石油学报, 2015, 36 (1) : 67-73. Liu Jingshou, Dai Junsheng, Wang Ke, et al. An Approach to Correct the Attitudes of Fracture for Deviated Borehole in Core and Its Application[J]. Acta Petrolei Sinica, 2015, 36 (1) : 67-73. |
| [28] | 李俊英, 李培良. 三轴不等应力场下剪切破裂趋势面方向探析[J]. 地学前缘, 2009, 16 (1) : 261-269. Li Junying, Li Peiliang. Analysis of the Direction of Shear Fracture Trend Surface in Triaxial Unequal Stress Fields[J]. Earth Science Frontiers, 2009, 16 (1) : 261-269. |
| [29] | 薛冈, 卢华复, 朱成宏, 等. 伸展区域平衡剖面法及其在构造分析中的应用[J]. 高校地质学报, 2001, 7 (4) : 427-434. Xue Gang, Lu Huafu, Zhu Chenghong, et al. Structure Restoration of Balancing Cross Section in Extension Area[J]. Geological Journal of China Universities, 2001, 7 (4) : 427-434. |
| [30] | 汤济广, 梅廉夫, 沈传波, 等. 平衡剖面技术在盆地构造分析中的应用进展及存在的问题[J]. 油气地质与采收率, 2006, 13 (6) : 19-22. Tang Jiguang, Mei Lianfu, Shen Chuanbo, et al. Advances and Problems in the Application of Balanced Cross-Section Technique in Structure Studies of Basins[J]. Petroleum Geology and Recovery Efficiency, 2006, 13 (6) : 19-22. |